- マンハッタン距離ってなに?
- マンハッタン距離の計算方法は?
- マンハッタン距離ってどんな場面で使うの?
こんにちは!しゅんです!
今回はマンハッタン距離について解説していきます!
例えば2つの点がどれだけ離れているかを求めるとき、まずは下のような距離を計算すると思います。
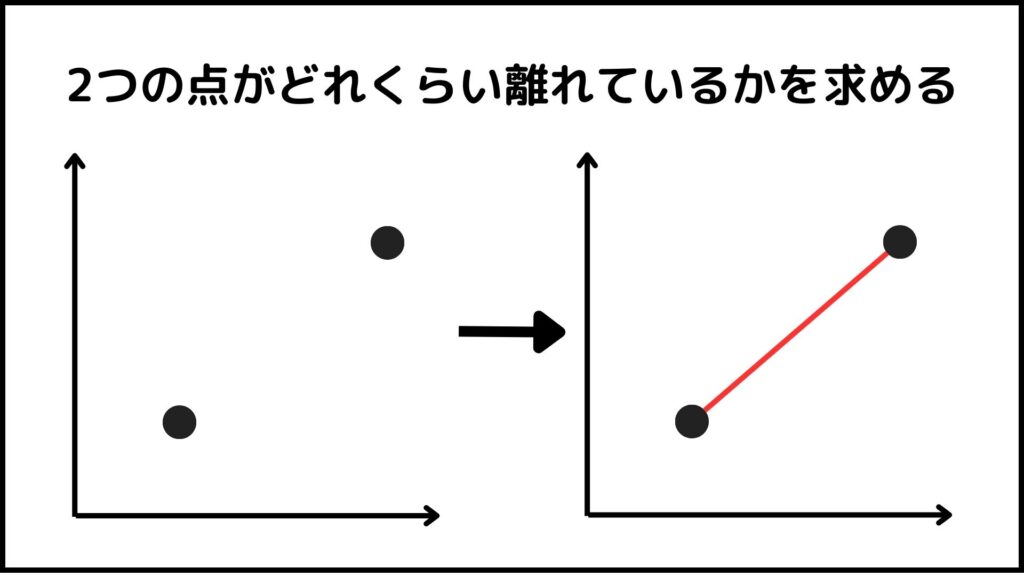
このように2つの点を直線で結んだときの長さをユークリッド距離と呼びます。ユークリッド距離はおそらく最も一般的な距離だと思います。
でも2つがどれくらい離れているかを求める方法は他にもあるんです。そしてそのうちの1つがマンハッタン距離です。
それでは解説していきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
マンハッタン距離ってなに?
マンハッタン距離は2つの点がどれくらい離れているかを下図のように求めます。
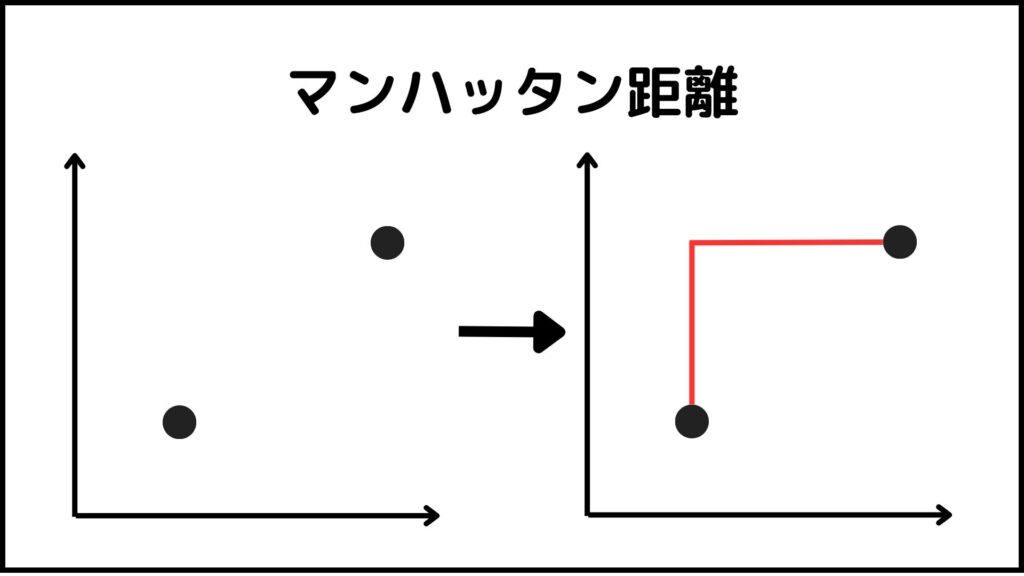
2つの点を直線で結ぶのではなく直角に線を曲げて距離を求めます。例えば2つの点の座標が(1,1)と(2,2)だったとしましょう。
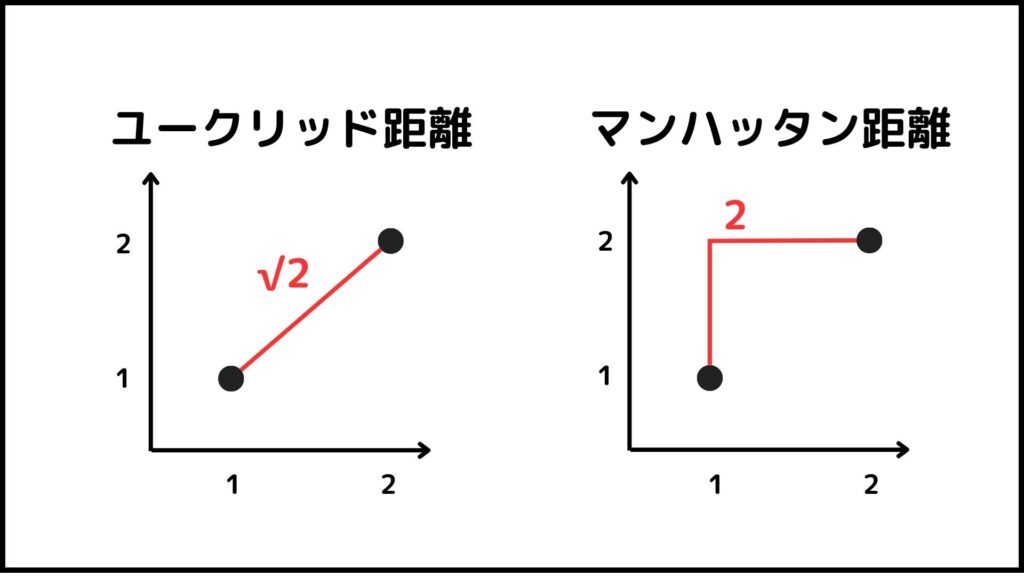
このときユークリッド距離とマンハッタン距離はそれぞれ
ユークリッド距離:\(\sqrt{2}\)
マンハッタン距離:\(2\)
となります。
マンハッタン距離の計算方法
2次元平面におけるユークリッド距離とマンハッタン距離の計算方法を以下の通りです。
ユークリッド距離:\(d(x,y) = \sqrt{(x_1-y_1)^2+(x_2-y_2)^2}\)
マンハッタン距離:\(d(x,y) = |x_1-y_1|+|x_2-y_2|\)
但し\(x = (x_1,x_2), \; y = (y_1,y_2)\)とする。
例えば(1,3)と(8,7)の2点の間のマンハッタン距離を求めると
\(|1-8|+|3-7|=11\)
となります。
マンハッタン距離ってどんな時に使うの?
マンハッタン距離は例えば京都みたいな都市において2地点がどれくらい離れているかを求めるときとかに使います。
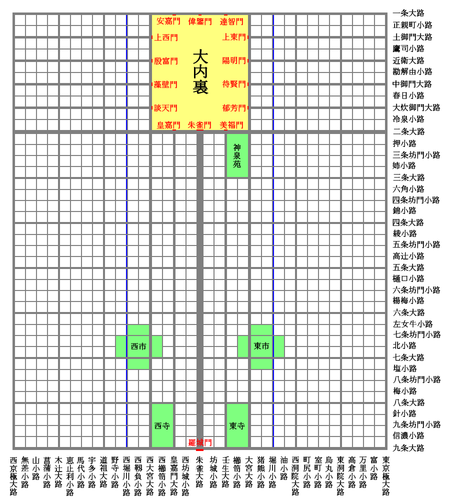
Wikipediaより引用 : 京都市内の通り – Wikipedia
京都の町は碁盤の目のようになっていて、このような区画だとマンハッタン距離の方が有用です。
イメージ的にはユークリッド距離とマンハッタン距離の違いは距離と道のりの違いみたいな感じですね。
マンハッタン距離の語源もアメリカのマンハッタンという都市における車の走行距離らしいです。
ぼくは最近傍探索でマンハッタン距離を勉強しましたが他にも都市計画、ゲーム理論、生物学、画像処理など様々な所で使われているようです。
\\\ 最近傍探索はこちらの記事で解説しています! ///
おわりに
いかがでしたでしょうか。
今回の記事ではマンハッタン距離について解説していきました。
ぼくが勉強している経営工学でも結構登場する重要な距離の概念です。一般的なユークリッド距離以外にも求め方があるなんてびっくりですね。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。



