こんにちは！しゅんです！
今回はチェビシェフの不等式について解説していきます！
チェビシェフの不等式は確率・統計で登場する数学用語です。この記事ではチェビシェフの不等式について図を使って分かりやすく解説していきます。
それでは解説していきましょう！
統計検定2級に関する他の記事はこちらから見れます！
ぜひ他の記事も読んでみてください！
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます！
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学（けいえいこうがく、英: engineering management）は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
チェビシェフの不等式ってなに？
まず最初にチェビシェフの不等式がどんなものなのかを説明したいと思います。
期待値\(\mu\), 分散\(\sigma^2\)を持つ確率分布に従う確率変数\(X\)があるとします。
このときどんな\(k\)に対しても下の不等式が成り立ちます。
\(P(|X-\mu| \geq k\sigma) \leq \frac{1}{k^2}\)
この式は\(|X-\mu|\)が\(k\sigma\)以上になる確率が必ず\(\frac{1}{k^2}\)以下になるということを表しています。
といってもこれだけで何を言っているか理解するのは難しいですよね。ということでここからはこのチェビシェフの不等式が具体的どんなことを言っているのかを、正規分布を用いてなるべく分かりやすく説明したいと思います。
シグマ範囲ってなに？
正規分布のグラフ
初めに正規分布のグラフについておさらいしましょう。
下のグラフは期待値\(\mu=50\), 分散\(\sigma^2=100\)の正規分布の確率密度関数です。
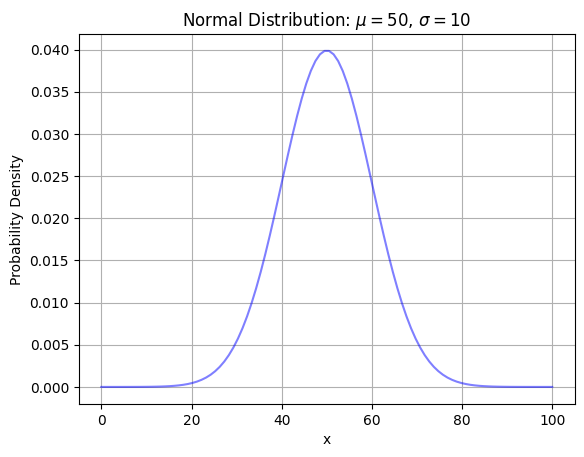
例えばこの正規分布に従う確率変数が40から60の間にある確率は下の水色の面積を計算することで求められます。
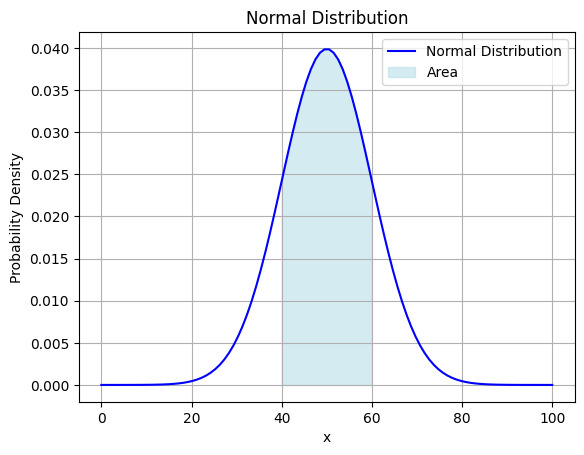
この水色の面積を計算するとだいたい0.68くらいです。つまりこの正規分布に従う確率変数が40から60の間にある確率は約0.68だということを表しています。
正規分布はこちらの記事で詳しく解説しています！
1シグマ範囲
それでは次に上の正規分布を使って1シグマ範囲について説明したいと思います。
シグマとは標準偏差\(\sigma\)のことです。例えば上の正規分布は分散\(\sigma^2=100\)なので標準偏差は\(\sigma=10\)となります。
1シグマ範囲とは、平均（期待値）\(\mu\)から\(+\sigma,\;-\sigma\)だけ離れた範囲のことです。
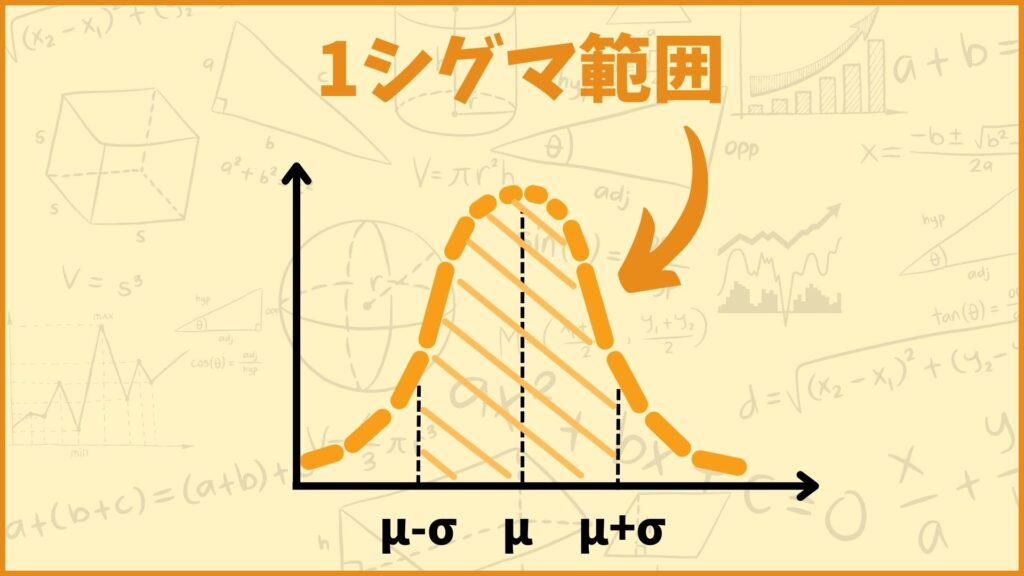
さっきの正規分布で言うと、\(\mu=50,\;\sigma=10\)なので1シグマ範囲は40から60の間という風になります。
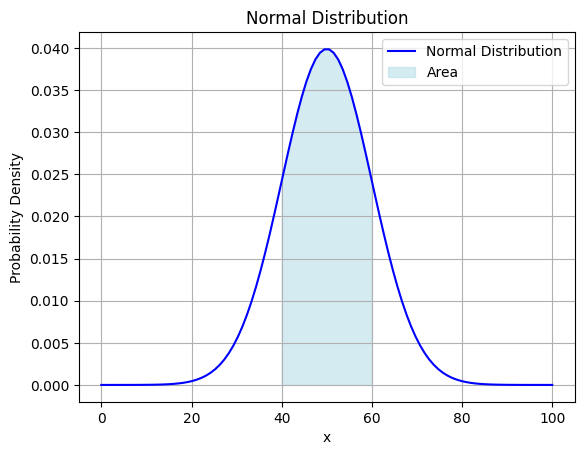
この「確率変数\(X\)が1シグマ範囲の中にある」ということを式で表すと下のようになります。
\(\mu-\sigma \leq X \leq \mu+\sigma\)
さらにこの式を絶対値を使って表すと下のようになります。
\(|X-\mu| \leq \sigma\)
それでは\(X\)が1シグマ範囲の中にある確率はいくつになるでしょうか。上の正規分布でいうと、40から60の間にある確率を求めれば計算できます。これはさきほど約0.68だと計算できました。
つまり\(X\)が1シグマ範囲の中にある確率は約0.68となります。このことを式で表すと下のようになります。
\(P(|X-\mu| \leq \sigma)\)
\(=P(|X-50| \leq 10)\)
\(=0.683…\)
今度は下のグラフの水色の面積を求めてみましょう。
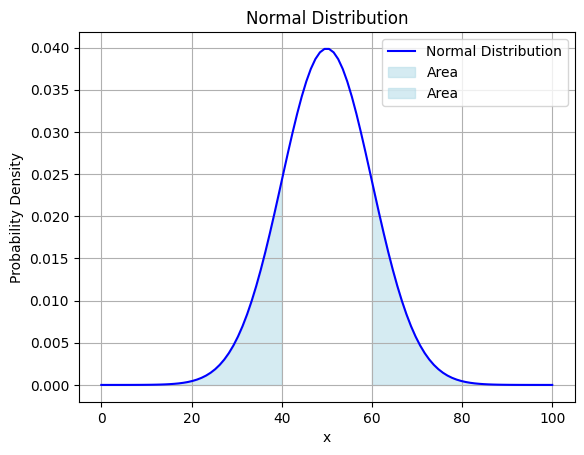
この水色の範囲はすべての範囲から1シグマ範囲を除いた部分を表しています。
確率変数\(X\)がこの範囲にあることを下のように表します。
\(X \leq \mu-\sigma, \; \mu+\sigma \leq X\)
さらにこの式を絶対値を使って表すと以下のようになります。
\(|X-\mu| \geq \sigma\)
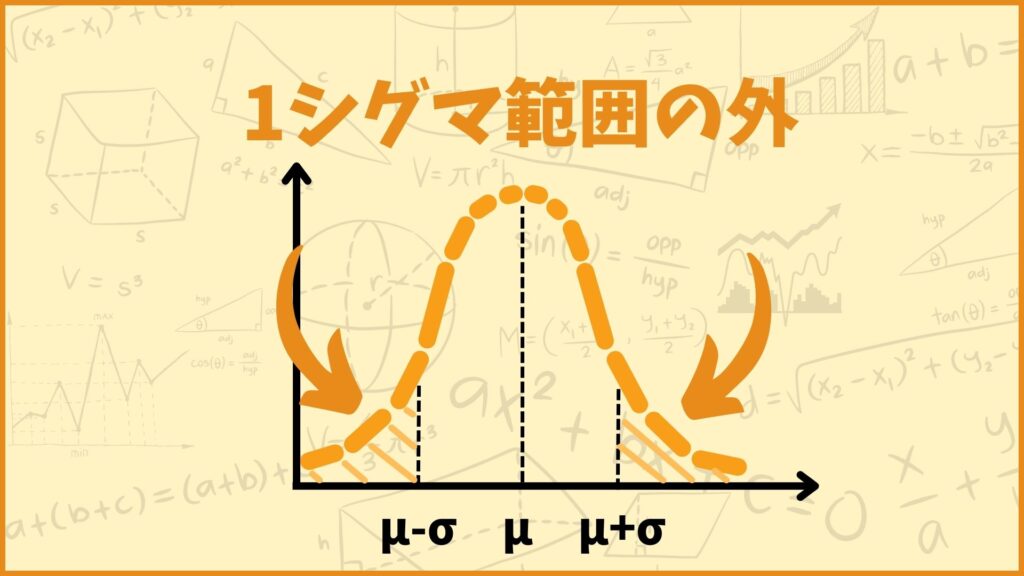
それでは\(X\)が1シグマ範囲の外にある確率はいくつになるでしょうか。結論1から1シグマ範囲の中にある確率を引き算すれば計算できます。
確率密度関数はすべての範囲の面積が必ず1になります。
イメージ的には確率の余事象みたいな感じです。
（余事象は高校数学で勉強すると思います！）
例えばさっきのグラフの例で言うと1シグマ範囲の中にある確率は約0.68だったので、1シグマ範囲の外にある確率は約0.32となります。
このことを数式で表すと以下のようになります。
\(P(|X-\mu| \geq \sigma)\)
\(=P(|X-50| \geq 10)\)
\(=1-0.683…\)
\(=0.317…\)
なんかこの式チェビシェフの不等式に似ていますね。後で説明しますが、1番上の式がチェビシェフの不等式の\(k=1\)バージョンになっていますね。
2シグマ範囲
次に2シグマ範囲について説明したいと思います。といってもほとんど1シグマ範囲と同じなので説明は簡単にしたいと思います。
2シグマ範囲はその名の通り平均（期待値）\(\mu\)から\(-2\sigma, \; +2\sigma\)だけ離れた範囲を指します。
1シグマ範囲よりももっと広いですね。例えばさっきの正規分布で言うと、期待値\(\mu=50\)、標準偏差\(\sigma=10\)なので、30から70の間が2シグマ範囲ということになります。
この範囲の面積を計算すると約0.95となります。つまりこの正規分布に従う確率変数が30から70の間に入る確率が約95%ということです。
逆に言うとこの2シグマ範囲の外に入る確率は約5%だということです。
このことを式で表すと以下のようになります。
\(P(|X-\mu| \geq 2\sigma)\)
\(=P(|X-50| \geq 20)\)
\(=1-0.954…\)
\(=0.046…\)
なんかこの式チェビシェフの不等式に似ていますね。後で説明しますが、1番上の式がチェビシェフの不等式の\(k=2\)バージョンになっていますね。
チェビシェフの不等式とシグマ範囲
チェビシェフの不等式の左辺はシグマ範囲の外
ここまで1シグマ範囲と2シグマ範囲の話をしてきましたが、これらはチェビシェフの不等式と非常にかかわりが深いんです。もう一度チェビシェフの不等式を載せておきます。
\(P(|X-\mu| \geq k\sigma) \leq \frac{1}{k^2}\)
この式の左辺って今まで説明してきたシグマ範囲の外とほぼ同じ形をしていますね。
\(P(|X-\mu| \geq k\sigma)\)
\(k=1\)のときは1シグマ範囲の外だし、\(k=2\)のときは2シグマ範囲の外です。例えば\(k=10\)を代入したら10シグマ範囲の外になります。
\(P(|X-\mu| \geq \sigma)\)
\(P(|X-\mu| \geq 2\sigma)\)
\(P(|X-\mu| \geq 10\sigma)\)
つまりこのチェビシェフの不等式はどんな\(k\)に対しても
確率変数\(X\)が\(k\)シグマ範囲の外にある確率は\(\frac{1}{k^2}\)以下になる
ということを言っています。例えば\(k=2\)とすれば2シグマ範囲の外にある確率は\(\frac{1}{2^2}=\frac{1}{4}=0.25\)以下であるということを言っています。
これまでの説明で使っていた正規分布で実際に計算した結果だと約0.05なのでちゃんとこのチェビシェフの不等式を満たしていますね。
もちろん\(k\)は整数じゃなくても大丈夫です。例えば\(k=2.5\)としたとき、2.5シグマ範囲の外にある確率は0.16以下になります。
\(P(|X-\mu| \geq 2.5\sigma) \leq \frac{1}{2.5^2}=0.16\)
チェビシェフの不等式はどんな確率変数に対しても成立する
ここまで正規分布を例にチェビシェフの不等式を説明してきましたが、実はチェビシェフの不等式はどんな確率分布に従う確率変数に対しても成立します。
これまで二項分布、幾何分布、ポアソン分布、指数分布など様々な確率分布について紹介してきましたが、全部チェビシェフの不等式が成立します。
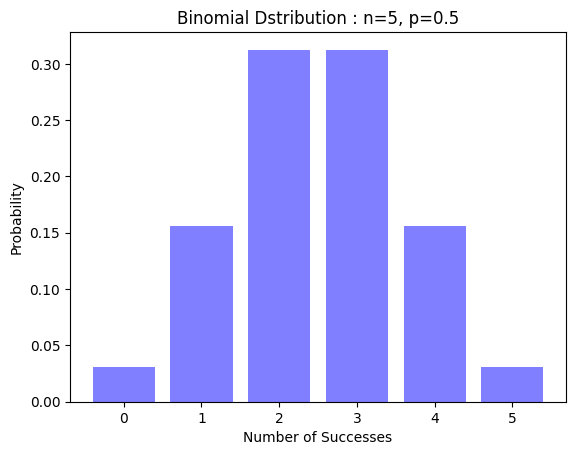
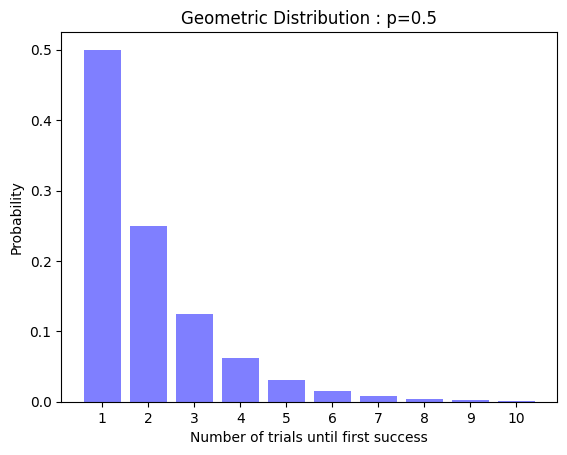
どんな確率変数でも成立するってのがすごいですよね。
どんな確率変数でも成立するってことはあんまり精度は良くないってことですよね笑
実用的には統計的推定で得られる信頼区間の方がよっぽど精度は良いです。
おわりに
いかがでしたか。
今回の記事ではチェビシェフの不等式について解説していきました。
今後もこのような経営工学に関する記事を書いていきます！
最後までこの記事を読んでくれてありがとうございました。
