こんにちは!しゅんです!
今回はポアソン分布について解説していきます!
ポアソン分布は確率・統計で登場する数学用語です。この記事ではポアソン分布について図を使って分かりやすく解説していきます。
また今回はpythonでポアソン分布を扱っていこうと思います。
それでは解説していきましょう!
統計検定2級に関する他の記事はこちらから見れます!
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
ポアソン分布ってなに?
ザックリ説明するとポアソン分布は珍しい現象が発生する回数に対する確率分布です。例えば一日に工場で生産される不良品の個数はポアソン分布に従います。
不良品が生産されることは結構珍しい現象です。例えばある工場では1日あたり平均5個の不良品が生産されるとしましょう。このとき、1日に生産される不良品の個数が3個である確率はいくつになるでしょうか?
詳しい計算式の説明は後でしますが結論不良品が3個生産される確率は以下の式で計算できます。
\(e^{-5} × \frac{5^3}{3!} = 0.140…\)
ということでだいたい0.14の確率で不良品が3個生産されることが分かりました。より一般的な話をしましょう。一定期間に平均\(\lambda\)回起こるような現象について、同じ期間内にその現象が\(x\)回起こる確率は下の計算式で求められます。
\(e^{-\lambda} × \frac{\lambda^x}{x!}\)
この式がポアソン分布の確率関数となります。
例えば1日の交通事故の件数が平均100件の地区において、その日一回も事故が起きない確率は下のように計算できます。
\(e^{-100} × \frac{100^0}{0!} =3.72 × 10^{-44}\)
計算結果はほぼ0となってしまいました。この地区で事故が一回も起きない日を見るためにははてしない時間が必要そうですね。(ちょっと計算してみたら約7.4正年必要でした笑)
\(f(x) = e^{-\lambda} × \frac{\lambda^x}{x!}\) \((x=0,1,2,…)\)
次の章ではなぜポアソン分布の確率関数がこのような計算式で表されるのかについて解説したいと思います。少し難しい話になるので分からなければ飛ばしても大丈夫です。
なぜこんな計算式になるの?
ポアソン分布は二項分布の特殊ケース
結論から言うとポアソン分布の公式は二項分布の式から導出することができます。
二項分布についてはこちらの記事で詳しく解説しています!
二項分布を簡単に説明すると一定の確率\(p\)で成功するようなベルヌーイ試行を\(n\)回やったときの成功回数が従う確率分布のことです。
二項分布の期待値は\(np\)ですが、これは成功確率\(p\)のベルヌーイ試行を\(n\)回やったときは平均的に\(np\)回成功するということを言っています。
先ほど説明したようにポアソン分布は一定期間に珍しい現象が発生する確率に関する分布です。めったに起きない珍しい現象なので、必然的に試行回数を大きくして考える必要があります。
つまりポアソン分布は試行回数\(n\)が非常に大きく、かつ成功する確率\(p\)が非常に低いという二項分布の特殊ケースについて扱っている分布なんです。
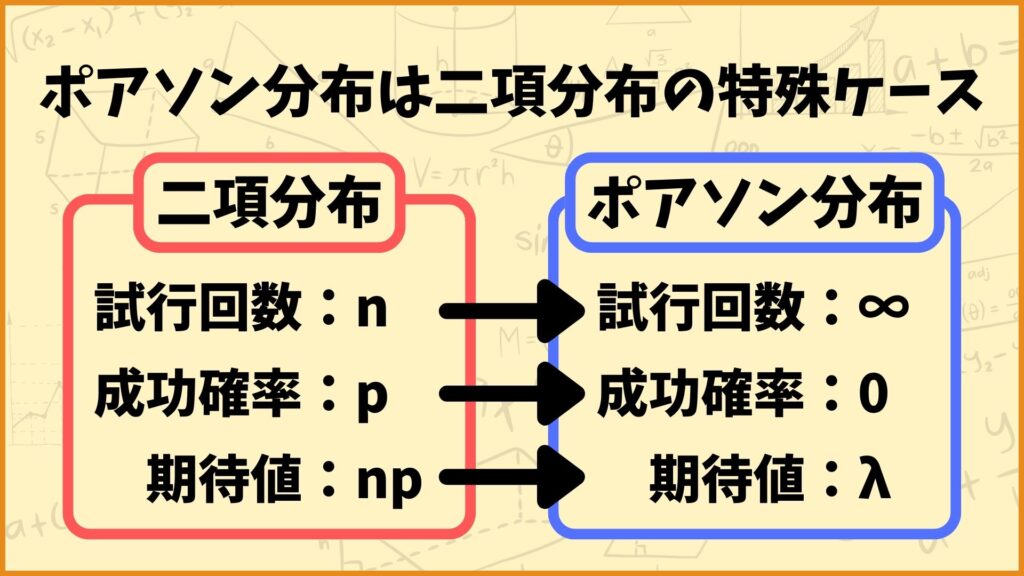
数学的には期待値\(np=\lambda\)を固定して、\(n→∞, \; p →0\)のように極限を取ることで二項分布はポアソン分布になります。というわけでここからは二項分布の確率関数を変形してポアソン分布の式を導出したいと思います。
二項分布の確率関数からポアソン分布の確率関数を導出する
\(P(X=x) \equiv \: _nC_x ×p^x × (1-p)^{n-x}\) \((x=0,1,2,…,n)\)
\(np=\lambda\)なので\(p=\frac{\lambda}{n}\)と表せます。これを二項分布の式に代入しましょう。
\(P(X=x)= \: _nC_x × (\frac{\lambda}{n})^x × (1-\frac{\lambda}{n})^{n-x}\)
この式を下のように変形していきます。
\(_nC_x × (\frac{\lambda}{n})^x × (1-\frac{\lambda}{n})^{n-x}\)
\(= \: \frac{n!}{x!(n-x)!} × (\frac{\lambda}{n})^x × (1-\frac{\lambda}{n})^{n-x}\)
\(= \: \frac{\lambda^x}{x!}(1-\frac{1}{n})(1-\frac{2}{n})…(1-\frac{x-1}{n}) ×(1-\frac{\lambda}{n})^{-x}(1-\frac{\lambda}{n})^n\)
最後に\(n→∞\)に飛ばしましょう。そうすると\((1-\frac{\lambda}{n})^n\)以外で\(n\)を含む部分は全て1に収束します。また\((1-\frac{\lambda}{n})^n\)の部分は\(e^{-\lambda}\)に収束します。
以上より下の式が導出されます。
\(e^{-\lambda} ×\frac{\lambda^x}{x!}\)
ポアソン分布の期待値と分散
ポアソン分布の期待値と分散は下のようになります。
期待値 : \(\mu = \lambda\)
分散 : \(\sigma^2 = \lambda\)
期待値はその確率分布が取る値の平均を表します。例えば\(\lambda=5\)のとき、発生回数は平均5回になるということを表しています。分散はその確率分布が取る値にどれだけばらつきがあるかを表します。
日常で見るポアソン分布の例
ポアソン分布は珍しい現象の発生回数を扱う分布ですが、結構色んな所で見かけます。日常での具体例があった方がイメージがつかみやすいと思うのでこの章ではいくつか日常の例を紹介していきます。
事故の件数
これは先ほども説明しましたが事故の件数はポアソン分布に従うことがあります。
例えば1日平均100件の事故がある地域で起きる事故の件数は\(\lambda=100\)のポアソン分布に従います。
確率関数 :
\(P(X=x) = e^{-100} × \frac{100^x}{x!}\) \((x=0,1,2,…)\)
期待値 : \(\mu = 100\)
分散 : \(\sigma^2= 100\)
電話がかかってくる回数
とある会社の受付で1時間あたり平均5件の電話がかかってくるとき、電話がかかってくる回数は\(\lambda=5\)のポアソン分布に従います。
これまでに説明した式で表すと以下のようになります。
確率関数 :
\(P(X=x) = e^{-5} × \frac{5^x}{x!}\) \((x=0,1,2,…)\)
期待値 : \(\mu = 5\)
分散 : \(\sigma^2= 5\)
ウェブサイトのクリック数
あるウェブサイトのクリック数が月間平均1000クリックだとすると、1カ月間のこのウェブサイトのクリック数\(x\)は\(\lambda=1000\)のポアソン分布に従います。

これまでに説明した式で表すと以下のようになります。
確率関数 :
\(P(X=x) = e^{-1000} × \frac{1000^x}{x!}\) \((x=0,1,2,…)\)
期待値 : \(\mu = 1000\)
分散 : \(\sigma^2= 1000\)
ポアソン分布をpythonで扱う
最後にpythonを使ってポアソン分布を扱いたいと思います。プログラミングの知識が必要なので、分からなければプログラムの所は飛ばして結果だけ確認してみてください。
事前準備
pythonで確率・統計を扱うときはscipyというライブラリをよく使います。その中でも今回はポアソン分布を扱いたいのでpoissonをインポートします。poissonはポアソン分布(poisson distribution)のことです。また数値計算でよく使うnumpy、グラフ作成でよく使うmatplotlibというライブラリもインポートしておきます。
import scipy.stats as stats
from scipy.stats import poisson
import matplotlib.pyplot as plt
import numpy as npポアソン分布の確率を計算する
ということでまずは平均値\(p\)を5としてポアソン分布の確率関数を計算します。例えばこの現象が3回起こる確率を計算してみましょう。
lambda_value = 5 # 平均値
x = 3 # 現象が3回発生
probability = poisson.pmf(x, lambda_value) # 平均5回起こる現象が3回起こる確率を計算
print("P(X = 3) =", probability) # 結果を表示
ということで平均値が5のポアソン分布において、ある現象が3回起こる確率は約0.14であることが分かりました。
ポアソン分布の確率関数をグラフ化する
次にこのポアソン分布をグラフ化してみましょう。平均的に5回発生する現象が、0回、1回、2回、3回、…という風に発生する確率をグラフで表したいと思います。
# 平均値λの設定
lambda_value = 5
# xの範囲を指定(0から15までの整数)
x_values = range(0, 16)
# 確率密度関数の値を計算
probabilities = [poisson.pmf(x, lambda_value) for x in x_values]
# グラフのプロット
plt.bar(x_values, probabilities, color = "blue", alpha = 0.5)
plt.xlabel('x')
plt.ylabel('P(X = x)')
plt.title('Poisson Distribution (λ = 5)')
plt.xticks(np.arange(0,16,1))
# グラフの表示
plt.show()
ということでこの図をみると\(x\)が4,5のときに確率が最も大きくなって、そこからまた確率が小さくなっていますね。例えば\(x \geq 10\)の範囲を見てみると確率がほぼ0になっていますね。
これは例えば一時間で平均5回起こる現象が10回以上起こる確率はめちゃめちゃ低いということですね。
グラフでは15回までしか表示していません。16回目以降も存在しますが、ほぼ0で違いが分かりづらいので15回目まで表示しました。
ポアソン分布の累積分布関数をグラフ化する
累積分布関数とは、それまでの確率を全部足し算した関数です。例えば\(x=2\)のときポアソン分布の累積分布関数は、ある現象が0回発生する確率、1回発生する確率、2回発生する確率を足し算した値になります。
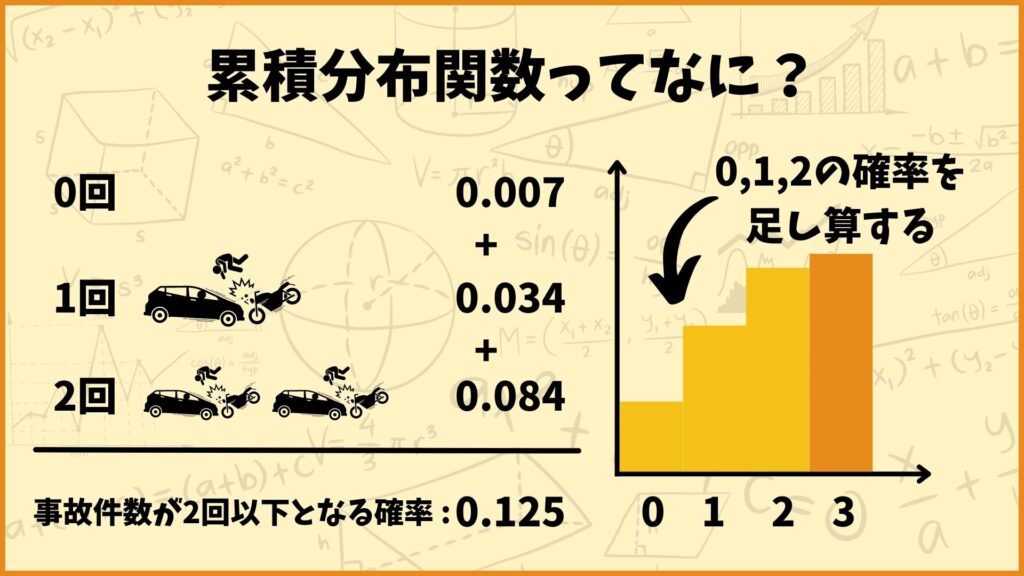
それではpythonで累積分布関数をグラフ化してみましょう。\(\lambda=5\)のポアソン分布の累積分布関数を作成します。
# 平均値λの設定
lambda_value = 5
# xの範囲を指定(0から15までの整数)
x_values = range(0, 16)
# 累積分布関数の値を計算
cumulative_probabilities = [poisson.cdf(x, lambda_value) for x in x_values]
# グラフのプロット
plt.plot(x_values, cumulative_probabilities, marker='o', linestyle='-', color = "blue", alpha = 0.5)
plt.xlabel('x')
plt.ylabel('P(X <= x)')
plt.title('Cumulative Distribution Function (Poisson, λ = 5)')
plt.xticks(np.arange(0,16,1))
plt.yticks(np.arange(0,1.1,0.1))
# グラフの表示
plt.show()
このグラフを見ると\(x=8\)の値が0.9を超えているのが分かりますね。つまり90%以上の確率で発生回数が8回以下になるということです。
シミュレーションしてみる
それでは実際にシミュレーションしてみましょう。平均値を\(\lambda=5\)としたときに、その現象が何回発生するかを記録します。この記録を10回、100回、1000回、10000回という風に行ったときに結果がどのような分布になるかをpythonでシミュレーションしていきたいと思います。
プログラムは試行回数が10回のときのものを表しています。5行目の数字を変えることで好きな試行回数にすることができます。
# 平均値λの設定
lambda_value = 5
# 試行回数(ここを好きな数値に変更する)
num_trials = 10
# 結果を格納するリスト
result = []
# ポアソン分布に従って試行を行う
for i in range(num_trials):
# 発生回数を求める
occurrences = np.random.poisson(lambda_value)
# 発生回数をリストに追加する
result.append(occurrences)
# ヒストグラムを描画する
plt.hist(result, bins=range(1, max(result) + 2), align="left", rwidth=0.8, density=True, color = "blue", alpha = 0.5)
plt.xlabel("Number of Occurrences")
plt.ylabel("Probability")
plt.title("Poisson distribution with λ=5 and {} trials".format(num_trials))
plt.xticks(np.arange(0,max(result)+1,1))
plt.show()
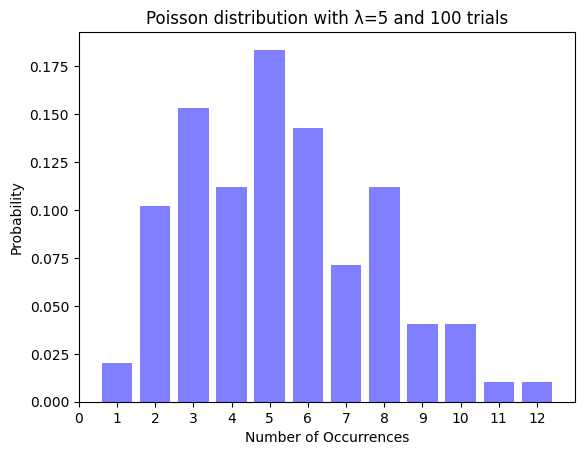
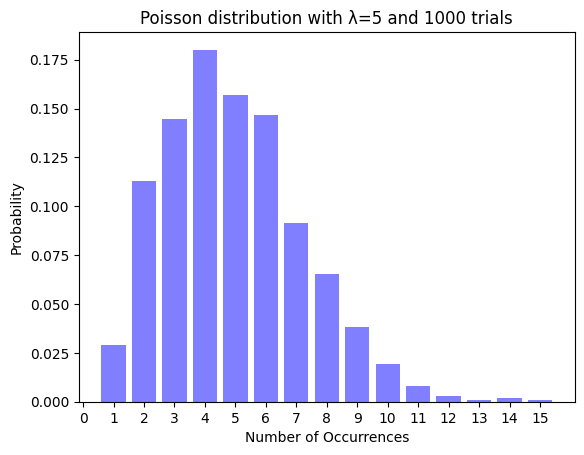

このグラフは横軸が発生回数、縦軸がその回数が結果として現れた確率を表しています。
左上から順番に10,100,1000,10000回となっています。10回の場合は思っている形とは全然違いますが、回数を増やすにつれてグラフの形が確率分布と同じようになっているのが分かると思います。
つまり確率分布とは、とある試行をたくさんやっていったら各結果の出現確率はこのような分布になっていくんだよってことを表しているんですね。
期待値をグラフで確認する
最後に期待値についてもグラフを使って確認してみましょう。先ほどの平均値\(\lambda=5\)のポアソン分布に従う試行を10,100,1000,10000回と増やしていったときに、各回数で得られた結果の平均値がどのように推移していくかをグラフを使って確認してみましょう。
lambda_value = 5 # ポアソン分布の平均値
n_sim = [10, 100, 1000, 10000] # 試行回数を設定
result = [] # 平均値を格納するための空リストを作成
for n in n_sim:
simulated_data = np.random.poisson(lambda_value, n) # ポアソン分布に従う乱数を生成
mean = simulated_data.mean() # 乱数の平均値を計算
result.append(mean) # 結果に平均値を格納
# グラフを描画する
plt.plot(n_sim, result, marker="o", color="blue", alpha=0.5, label="Simulated")
plt.hlines(lambda_value, 10, 10000, color="orange", label="Theoretical")
plt.xscale("log")
plt.xlabel("Number of trials")
plt.ylabel("Average number of trials until success")
plt.title("Poisson distribution with lambda = 5")
plt.legend()
plt.show()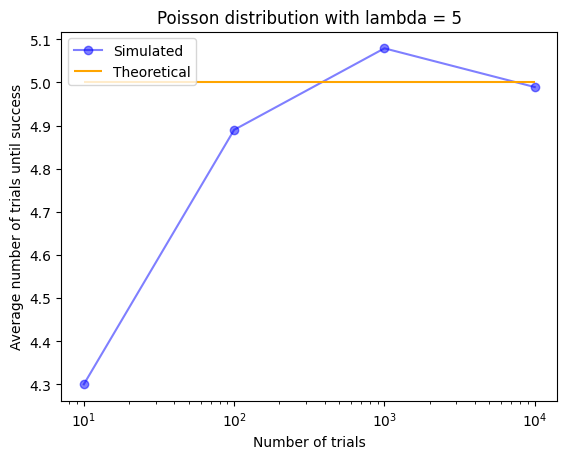
橙線は期待値で5のラインを表しています。つまり橙線は理論的にはある現象が\(\lambda=5\)のポアソン分布に従うときその現象は平均5回発生するということを言っています。
一方青線は実際にシミュレーションした結果その現象が平均何回発生したかを表しています。試行回数が少ないときは期待値との誤差がありますが、試行回数が多くなるにつれてどんどん期待値に近づいているのが分かりますね。
ランダムに試行されるのでプログラムを実行するたびにグラフは変わりますが、基本的には試行回数が大きくなるにつれて誤差は小さくなっていくはずです。
おわりに
いかがでしたか。
今回の記事ではポアソン分布について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。




