こんにちは!しゅんです!
今回は多項式回帰について解説していきたいと思います。
多項式回帰は回帰分析の中でも予測モデルが多項式になる分析です。ぼくがデータ分析の勉強をしていたときにでてきたので皆さんにもシェアしたいと思います!また今回は説明と一緒にpythonを使ってどんなものか確かめたいと思います。
それでは解説していきましょう!
普段はNBAのデータ分析をしたりしています。
ぜひこちらの記事も読んでみてください!
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
多項式回帰ってなに?
ザックリ説明すると多項式回帰は直線じゃないデータを予測することです。下の例を見てみましょう。

上の表はあるアイスクリーム屋の1年間の売上データです。これを横軸が月、縦軸が売上のグラフで表したのが下の図です。
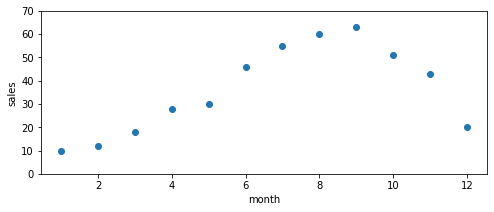
今回はこのデータを回帰で予測したいと思います。しかしここで1つ問題がでてきます。
これ直線では予測できなさそうですよね。
直線で予測できそうな場合は線形回帰が使えるんですけど、今回の場合はそう簡単にはいかなさそうです。
こちらの記事で線形回帰について説明しています!
こんなときに使える手法の中の1つが多項式回帰です。
※線形回帰じゃない回帰のことを一般に非線形回帰と呼びます。したがって今回説明する多項式回帰は非線形回帰の一種だと言えます。その他にも指数関数や対数関数など非線形回帰で使う関数モデルはたくさんあります。
例えば今回の例で言うと下の図のような曲線で回帰ができそうですよね。

ということで今回はこの多項式回帰をpythonでやる方法を説明したいと思います!
次の章ではもう少し具体的な説明をしたいと思います。高校で学ぶ数学の知識が必要なので難しいと感じるかもしれませんが、本格的にデータ分析を勉強するには数学の知識が必須なのでできたら知っておきたいものですね。
線形(単)回帰と多項式回帰の数学的な違い
線形(単)回帰
線形(単)回帰は中学生で習う一次関数を使って予測をします。
一次関数は以下のような関数です。
y = ax + b (a, bは定数)
線形(単)回帰では最小二乗法という手法を使って、xを入力したときに返ってくるyの予測値が実際のyの値とどれくらい近いかを測っています。a,bの値を変えれば実測値と予測値の近さは変わります。その中でも最も実測値と予測値が近いa,bを見つけるのが線形回帰がやっていることです。
この一次関数をグラフで表すと直線になりますよね。だから線形回帰は直線で予測する回帰なんです。
※より詳しく説明すると線形回帰が直線になるのは2次元のときの話です。3次元では平面となり、4次元以降は図で表すのが難しくなります。ただ今回はxとyしか使わない2次元平面の話なので線形=直線だと考えて大丈夫です。また2次元での線形回帰のことを特別に線形単回帰と呼んだりします。この後説明する線形回帰は全て線形単回帰だと思ってください。
多項式回帰
多項式回帰は以下のような式で表されます。
y = a0 + a1x + a2x^2 + a3x^3 + ・・・ + anx^n
(a0~anは定数のn次多項式)
多項式回帰の場合はxの次数が増えます。例えば3次の多項式回帰だったらx^3まで、10次の多項式回帰だったらx^10までを使って予測をします。線形回帰のときと一緒で、xにデータを入力したときyから予測値が返ってくるんですが、この予測値と実測値が最も小さくなるようなa0~anの組み合わせを見つけるのが多項式回帰がやっていることです。
xの次数を増やすことによって予測できるデータの幅が広がります!
例えば高校で習う二次関数や三次関数は曲線ですよね。さらに4、5と次数を増やすほどくねくねしていました。このようにxの字数を増やすことによって予測性能を上げることができるんです。
※実は次数が多ければ多いほど良いってわけでもないんです。これは過学習と呼ばれる現象で、与えらえたデータについての学習をしすぎて未知のデータを予測できなくなってしまうことを指します。
後半でより詳しい説明をします。
それでは実際に多項式回帰をpythonでやってみましょう!
多項式回帰をpythonでやってみる
手順は以下の通りです。
今回はnumpyとmatplotlibを使います。
多項式回帰には必要のないステップですが視覚的にわかりやすいので一応…
PolynomialFeaturesを使います。また次数は自分で設定できますが、今回は3次でやってみたいと思います。
多項式回帰を実行します。
ちゃんと予測できているかをグラフで確かめます。
また今回はgoogle colabを使ってやってみたいと思います。google colabはgoogleが無料で提供している開発環境です。google colab上ではpythonを使って様々なデータ分析や機械学習の手法をプログラムして実行することができるので非常に便利です。
STEP.1 事前準備、データの作成
データの作成にはnumpy、そしてグラフ作成にmatplotlibを使いたいと思います。どちらもデータ分析をするにはかかせない便利なやつです。ということでまずはこれらをインポートしましょう。
# numpyをnpとしてインポート
import numpy as np
# matplotlibをpltとしてインポート
import matplotlib.pyplot as pltasの後ろに書いてあるのは省略形です。これ以降numpyを使いたかったらnp、matplotlibを使いたかったらpltと書けば大丈夫です。
それでは次に今回使うデータを作りましょう。Xに月データを、yに売上データを格納します。
# 月データを作成
X = np.arange(1,13)
# 売上データを作成
y = np.array([10,12,18,28,30,46,55,60,63,51,43,20])np.arange()は連番や数列を作ることができるやつです。今回は1から12までの連番データを作りたいのでカッコの中は1,13とします。np.array()は配列を作ることができるやつです。便利なリストみたいな感じです。
STEP.2 グラフを作成
多項式回帰には直接関係あるわけではないですが視覚的にもわかりやすいので一応コードを載せておきます。説明は飛ばすので気になる人は調べてみてください。「python グラフ」などで調べたらわかりやすいmatplotlibの記事がでてきます。
# グラフを作成
plt.figure(figsize=(8,3))
plt.scatter(X, y)
#yの上限、下限を設定
plt.ylim([0,70])
#x軸のラベルを設定
plt.xlabel("month")
#y軸のラベルを設定
plt.ylabel("sales")
#グラフを表示
plt.show()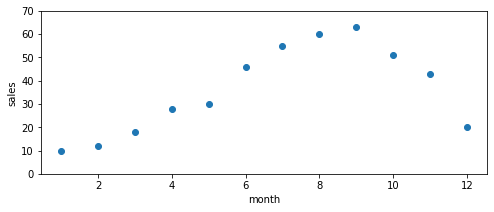
STEP.3 3次までの特徴量を生成
今回は3次の多項式を使って回帰を行いたいと思います。べき乗の生成にはPolynomialFeaturesという便利なものを使います。
# scikit-learnからPolynomialFeaturesをインポート
from sklearn.preprocessing import PolynomialFeaturesそれでは実際に3次までの特徴量を生成しましょう。
# 1, x, x^2, x^3 という4つの特徴量を作成するための前処理
X = X.reshape(-1,1)
polynomial_features = PolynomialFeatures(degree=3) #degreeで次数を変えられる
# 各列が 1, x, x^2, x^3 となる4列のデータが生成される
X_poly = polynomial_features.fit_transform(X)ということでこの時点で3次の多項式回帰をするための説明変数の準備ができました。(説明変数とは入力するデータのこと。今回は月データ)
コードの説明ですが、まず.reshape(-1,1)は回帰分析をするときによくやる操作です。実は回帰分析の説明変数においてnumpyの配列をそのまま適用することはできないんです。そのため.reshape(-1,1)をすることによって分析できるような形に変えます。(目的変数は変えなくて大丈夫です。)
次にPolynomialFeaturesを使って1, x, x^2, x^3までの特徴量を作ります。degreeの数字を変更することによって何次まで生成するかを決めることができます。今回は3次まで生成したいので3にします。後でdegreeの数字を色々いじってみたいと思います。
最後にX_polyに3次までの特徴量を生成します。X_polyの中身は下のようになっています。

1から10までの月データを表示しています。このようにX_polyには1列目に1, 2列目にx, 3列目にx^2, 4列目にx^3の特徴量が格納されています。これを説明変数として使いたいと思います。
STEP.4 多項式回帰の実行
それでは実際に多項式回帰をやっていきましょう。まずは回帰に必要なやつをインポートします。
# 多項式回帰に必要なやつをインポート
from sklearn.linear_model import LinearRegressionあれって思った人がいるかもしれません。というのも LinearRegressionは線形回帰という意味です。先ほど多項式回帰は線形回帰じゃ表せないデータを予測するときに使うと言ったので、なんでここでLinearRegressionがでてくるんだと思うと思います。
実は多項式回帰は線形回帰を使ってできちゃうんです。
少し難しくなりますが、それぞれの項を別物だとして考えてみれば(例えばxの項をx1, x^2の項をx2, x^3の項をx3と考える)この回帰分析は線形重回帰分析になります。
もし難しいと感じた場合は、多項式回帰に限っては非線形回帰のはずだけど工夫すれば線形回帰として扱うことができると思ってください。
それではモデルの学習をします。説明変数にはX_poly、目的変数にはyを使います。
# モデルの学習
reg = LinearRegression()
reg.fit(X_poly, y)これで多項式回帰が実行されました。
STEP.5 結果をグラフで表示
それでは最後に下のグラフを作成しましょう。
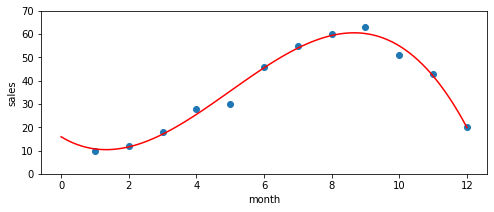
赤い曲線が多項式回帰で得られた回帰曲線です。
下のやつがこのグラフを表示するコードになります。
# 回帰曲線用データの作成
X_val = np.linspace(0,12, 100)
X_val = X_val.reshape(-1,1)
# 回帰曲線用データに対して 1, x, x^2, x^3 という 4 列の特徴量を作成する
X_poly_val = polynomial_features.fit_transform(X_val)
# 回帰曲線用データに対する予測
y_pred = reg.predict(X_poly_val)
# グラフを作成(figsizeでサイズを決める)
plt.figure(figsize=(8,3))
# 実測値(青点)をプロット
plt.scatter(X, y)
# 予測値(赤線)を表示
plt.plot(X_val,y_pred,c="red")
# y座標の上限と下限を設定
plt.ylim([0,70])
# x座標のラベルを設定
plt.xlabel("month")
# y座標のラベルを設定
plt.ylabel("sales")
# グラフを表示
plt.show()まず回帰曲線を表示するためのデータを作ります。np.linspaceは指定した範囲を等間隔に区切った配列を作ります。今回は0~12の範囲を100等分したデータを作成しました。例えば100の所を13にすると[0, 1, … ,11,12]という配列ができます。イメージ的には100個のデータそれぞれに対して多項式回帰による予測値を求めてそれを折れ線グラフで表示すると言う感じです。そのため100をもっと小さい数字に変えると赤線はカクカクになるはずです。
そして先ほどと同じようにこれら100個のデータに対して予測値を求めるために.reshape()とPolynomialFeaturesでデータの形を整えます。
未知のデータ(今回は100個のデータ)に対して予測をしたい場合は.predict(目的変数)を使えばできます。今回は予測したデータにy_predと名付けました。
plt.figure以降は普通のグラフ作成と同じなので説明は省略します。
ということでここまでで無事多項式回帰ができました。それでは最後に過学習の話をして終わりたいと思います。
過学習ってなに?
さきほど多項式回帰は直線じゃ表せないデータに対して予測できると話しました。確かに次数を増やすことによってより予測が正確になります。例えば下のグラフは今回使ったデータに対して線形回帰を適用した結果です。
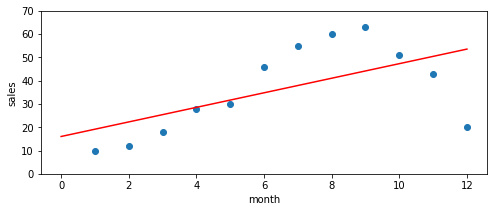
たしかにこれでは上手に予測ができてるとは言えなさそうですよね。
ここまでの話を聞いて、じゃあ次数をもっと増やせばよいんじゃないかと感じた人もいるかと思います。今回はdegreeを3にしましたが、これを10とか20とかにした方がもっと予測精度が高くなるんじゃないかと思うかもしれません。
ということでdegreeを大きくして多項式回帰をやってみましょう。下の図はdegreeが3,5,10,20の4パターンについて多項式回帰を実施した結果です。


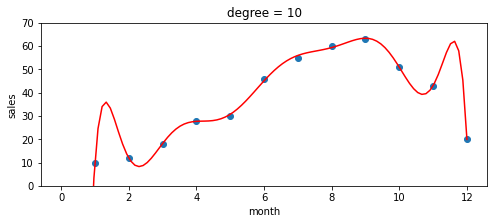

どうやら様子がおかしいですね。degreeが3、5のときはよく予測できていますが、10と20のときはぐにゃぐにゃになってしまっています。どうやらdegreeは大きければ良いというものでもなさそうですね。
このことを過学習と言います!
10と20を見てください。これらは予測モデルとしては適していないものの、青点はちゃんと通るようになっていますね。つまりすでに与えられたデータ(青点)に対してのみ学習しすぎた結果、未知のデータに対する予測(赤線)がうまくいかなくなっているんです。これが過学習です。
過学習を抑えるには自由度(degreeのこと)を調整したり正則化項を追加したりすることが考えられます。
過学習についてはまた別の記事で扱うかもしれません。
おわりに
いかがでしたでしょうか。
今回の記事ではpythonを使って多項式分析について説明していきました。こんな感じでプログラミングを使えばいろいろなことができます。非常に興味深いですよね。
データの数値をいじるとまた違う結果が得られるので興味がある人はぜひやってみてください!またこの記事では非線形回帰分析の中でも多項式分析について説明しました。他にも色々な手法があるので是非調べてやってみてください!
これからもこのようにプログラミングで色々やっていきたいと思います。ぼくが一番勉強になるので続けていきたいです!
最後までこの記事を読んでくれてありがとうございました。
この記事が役に立ったら幸いです。




