こんにちは!しゅんです!
いきなりですがもし無人島に行くとしたら何を持っていきますか?
持っていきたい物はたくさんあるけど、持っていける量には限りがあるので全部を持っていくことはできないですよね。
ということでこの記事ではこの問題をナップサック問題として扱って、一番満足がいくように無人島に持っていく物を決めていきたいと思います。また今回はpythonを使って実際にこの問題を解いてみたいと思います。
それでは解説していきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
今回使う数学の手法
今回の記事ではナップサック問題という数学の問題を使ってベストな組み合わせを選んでいきたいと思います。
ナップサック問題ってなに?
今あなたが無人島に行くと仮定します。無人島にはいくつか物を持っていくことができますが、最大でも10kgまでしか持っていけません。

さてあなたは10kgを超えないように無人島に何を持っていくでしょうか。当然物によって無人島に持っていきたい度合いが違いますよね。例えば扇風機よりも衣類の方が優先度が高いはずです。

ナップサック問題では全ての物に価値を設定します。例えば扇風機の価値は5で衣類の価値は100みたいに、無人島にどれくらい持っていきたいかで価値を決めます。
物の価値とはイメージ的にはそれを無人島に持っていけた場合の満足度みたいな感じです。
直観的に考えれば価値が大きい物から順番に持っていく方が良さそうですが、実はそう簡単にはいきません。なぜなら重さも考える必要があるからです。

例えば10kgまでしか選べないときに価値10、重さ10kgの物Aと価値6、重さ5kgの物B、価値5、重さ5kgの物Cから選ぶ時を考えます。価値だけ見たら物Aを選ぶのが一番良さそうに思えますが、この場合は物Bと物Cを選ぶ方が価値の合計が大きくなります。
このように、価値の合計を最大化するためには価値だけでなく重さも考える必要があります。無人島に持っていく物を選ぶ場合も同じように考えます。

上の図のようにそれぞれの物に対して価値と重さを設定し、10kgの上限を超えないように価値の合計が最大になるように物を選んでいきます。
例えば同じ物は1つまでしか選べない場合を考えると、結論フライパン、お米、衣類を持っていくのが一番価値の合計が大きくなります。
このようにある条件を満たすように、価値を最大にする組合せを見つける問題のことをナップサック問題と言います。
ナップサック問題の解き方はいくつかありますが、この記事ではパソコンに解いてもらうので省略します。アルゴリズムを知りたい方は是非調べてみてください!
ナップサック問題を数式で表す
ここまでは図や言葉での説明でしたが、ここからは実際に数式を使ってナップサック問題を表していきたいと思います。数式に表す問題は以下の通りです。
問題設定:
・無人島に持っていく物を選ぶ。
・無人島には合計で10kgまでしか運ぶことができない。
・同じ物は1つまでしか選ぶことができない。
・持っていける物の候補は以下の通りである。

問題:
10kg以内という条件を満たす組合せの中で、価値の合計が最大になる物の組み合わせを求める。
さっきの図の扇風機とかフライパンとかをA、Bで表しているだけです。この問題を数式を使って表していきます。
変数を定義する
まず変数\(x_i\)を用意します。この変数\(x_i\)は物\(i\)を持っていくなら1、持っていかないなら0を取るような0-1変数とします。
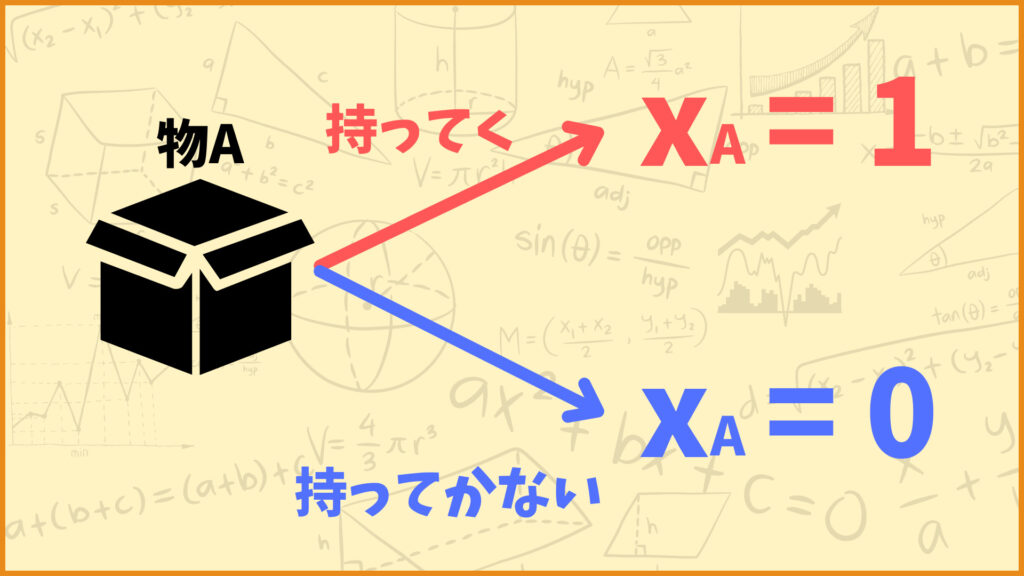
今回は物Aから物Eまであるので変数は\(x_A,\;x_B,\;x_C,\;x_D,\;x_E\)の5つです。
\(x_i \in \{0,1\}\;\;\;\;(i=A,\;B,\;C,\;D,\;E)\)
価値を数式で表す
次に価値について考えます。例えば物Aを持っていくと価値が5増え、持っていかないと価値は増えません。このことを変数\(x_A\)を使って\(5x_A\)と表すことができます。
同じように考えていくと、価値の合計は\(5x_A+50x_B+10x_C+25x_D+100x_E\)と表すことができます。

例えば物Aと物Cと物Dを持っていくとき\(x_A=x_C=x_D=1,\;x_B=x_E=0\)となります。このとき\(5+10+25=40\)となるので価値の合計は40という風に計算できます。
ナップサック問題ではこの価値の合計の式を最大にするように物を選んでいきます。
\(5x_A+50x_B+10x_C+25x_D+100x_E\)
重量制限を数式で表す
次に合計で10kgまでしか持っていけないという重量制限を数式で表していきます。例えば物Aを持っていくとしたときの重量は3kgになります。これを変数\(x_A\)を使って\(3x_A\)と表せます。
価値の合計のときと同じように考えていくと、重量の合計は\(3x_A+x_B+3x_C+2x_D+6x_E\)と表すことができます。

例えば物Aと物Cと物Dを持っていくとき\(x_A=x_C=x_D=1,\;x_B=x_E=0\)となります。このとき\(3+3+2=8\)となるので重さの合計は8kgという風に計算できます。
そしてこの重さの合計が10kg以下になることが条件なので、以上のことをまとめると重量制限の式は下のようになります。
\(3x_A+x_B+3x_C+2x_D+6x_E \leq 10\)
問題を数式で表す
以上のことをまとめると、今回の問題は以下のように数式で表すことができます。
\(\max{5x_A+50x_B+10x_C+25x_D+100x_E}\)
s.t. \(3x_A+x_B+3x_C+2x_D+6x_E \leq 10\)
\(\;\;x_i \in \{0,1\}\;\;\;\; (i=A,\;B,\;C,\;D,\;E)\)
これが無人島のナップサック問題を数式で表した結果です。一番オーソドックスなナップサック問題はこのような形を取ります。この問題を解くには動的計画法や分枝限定法などいくつかありますが、ここでは省略してpythonを使って解いてみます。
最大化(または最小化)したい式のことを目的関数と言ったりします。
(上の例でいう1行目の式)
また満たさなければいけない式を制約条件と言ったりします。
(上の例で言うと2,3行目の式)
pythonを使って問題を解く
それでは最後にpythonを使ってこの問題を解いてみましょう。今回はpythonのpulpという、数理計画法をpythonで扱うのに非常に便利なやつを使いたいと思います。
実行するコード
最終的には以下のコードを実行することで結果が得られます。
# pulpをインポート
! pip install pulp
from pulp import *
# LpMaximizeで最大化に設定
prob = LpProblem(sense=LpMaximize)
# 変数の定義
xA = LpVariable("xA", cat = LpBinary)
xB = LpVariable("xB", cat = LpBinary)
xC = LpVariable("xC", cat = LpBinary)
xD = LpVariable("xD", cat = LpBinary)
xE = LpVariable("xE", cat = LpBinary)
# 問題の設定
prob += 5*xA + 50*xB + 10*xC + 25*xD + 100*xE # 目的関数を設定
prob += 3*xA + xB + 3*xC + 2*xD + 6*xE <=10 # 制約条件を設定
prob.solve() # 問題を解く
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示
for x in prob.variables():
print(x,"=", value(x)) # 最適解を表示
上記のコードを実行すればこの画像のように答えが出てくるんですが、ぱっと見何をやっているか分からないので1つずつ解説します。
コードの説明
まず1~2行目でpulpをインポートしています。
# pulpをインポート
! pip install pulp
from pulp import *
4~5行目ではどのような問題を解くか指定しています。LpMaximizeだと最大化、LpMinimizeだと最小化に設定できます。今回は最大化したいのでLpMaximizeに設定します。
# LpMaximizeで最大化に設定
prob = LpProblem(sense=LpMaximize)
7~12行目では変数の定義をしています。LpVariableで変数を定義することができます。括弧の中で名前と変数が取りうる値を設定しています。今回は0-1変数にしたいのでLpBinaryとします。
# 変数の定義
xA = LpVariable("xA", cat = LpBinary)
xB = LpVariable("xB", cat = LpBinary)
xC = LpVariable("xC", cat = LpBinary)
xD = LpVariable("xD", cat = LpBinary)
xE = LpVariable("xE", cat = LpBinary)
14~16行目で問題の設定をしています。15行目では目的関数を設定し、16行目では制約条件を設定しています。
# 問題の設定
prob += 5*xA + 50*xB + 10*xC + 25*xD + 100*xE # 目的関数を設定
prob += 3*xA + xB + 3*xC + 2*xD + 6*xE <=10 # 制約条件を設定
18行目で問題を解いています。
prob.solve() # 問題を解く
20~24行目で結果を表示しています。21行目では解の状態を表示しています。Optimalなら最適解が求まっています。22行目では最適値、つまり最適解を代入したときの目的関数の値を表しています。23~24行目で最適解を表示しています。
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示
for x in prob.variables():
print(x,"=", value(x)) # 最適解を表示
これらのコードを実行した結果以下のように出力されました。

まず1行目のOptimalはこの問題を解いたら最適解が得られたことを表しています。
2行目は最適値がどれくらいかを示しています。つまり無人島に持っていく物の中で一番価値が高い組合せを選んだらその価値の合計が175だったということを表しています。
3~7行目は各変数の値を示しています。これを見ると物A,物D,物Eを持っていくのが価値の合計を最も大きくするということになります。
もう少しコードを短くする
変数を定義するときに毎回xA=…,xB=…みたいに書くのが面倒くさいので、まとめて書きます。他にも重さ、価値の情報をリスト化してまとめて書くこともできます。
# データの準備
c = [5,50,10,25,100] # 価値データをリスト化する
w = [3,1,3,2,6] # 重さデータをリスト化する
capacity = 10 # 重量制限データ
# LpMaximizeで最大化に設定
prob = LpProblem(sense=LpMaximize)
# 変数の定義(まとめて定義)
x = [LpVariable("x"+i, cat = LpBinary) for i in ("A","B","C","D","E")]
# 問題の設定
prob += lpDot(c, x) # 目的関数を設定
prob += lpDot(w, x) <= capacity # 制約条件を設定
prob.solve() # 問題を解く
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示
for x in prob.variables():
print(x,"=", value(x)) # 最適解を表示どっちも出力される結果は一緒になります。今回は変数の数が5個だったのでそこまで短くなっていないですが、変数の数が20個とかになるとこっちで書く方が全然短く書けます。
おわりに
いかがでしたか。
今回の記事ではナップサック問題について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。