こんにちは!しゅんです!
今回の記事ではナップサック問題で動的計画法を使うとどれくらい計算量が少なくなるのかを説明してみました!
動的計画法はある問題の最適解を見つけるために使われる手法です。計算した値をメモして2回目以降はメモの値を利用することによって計算量を減らすという手法です。
では実際にどれくらい実行時間が短くなるのでしょうか。それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
動的計画法を使うとどれくらい計算量が少なくなるの?
ナップサック問題の場合、動的計画法を使うのと使わないので計算量はそれぞれ以下のようになります。
動的計画法じゃないver ・・・\(O(2^n)\)
動的計画法ver・・・\(O(nx)\)
但し\(n\)は物の個数、\(x\)は重量制限
動的計画法じゃないverの計算量オーダーは指数時間で表されます。そのため物の個数\(n\)が増えると一気に計算時間が増えて、現実的に解くのが難しくなります。
一方動的計画法verの計算量オーダーは多項式時間で表されます。そのため物の個数\(n\)、重量制限\(x\)を増やしてもそこまで大幅に計算時間は増えません。
ここからはなぜこれらの計算量オーダーがそれぞれ上記のように表せるかを説明していきたいと思います!
ナップサック問題を解くための再帰式
ナップサック問題を解くために以下の再帰式を用いることを考えます。
物が\(n\)個あり、その中の最初の\(i\)個だけから選び、重量制限が\(x\)のナップサック問題を考える。この問題の最適値を\(P(i,x)\)とすると、以下の式が成り立つ。
\(\begin{equation} P(i,x)= \begin{cases}P(i-1,x) & (a_i>x) \\ \max\{P(i-1,x),\;P(i-1,x-a_i)+c_i\} & (a_i \leq x) \end{cases} \end{equation}\)
但し\(a_i\)は物\(i\)の重量、\(c_i\)は物\(i\)の満足度
今回はこの式を使って2つの計算量について考えていきたいと思います。
なぜこの再帰式が成立するのかはこちらの記事で解説しています!
問題の数と再帰式の計算時間が重要
計算量を考える上で重要なのは問題の数と再帰式の計算時間です。今回は下の再帰式を使うので、例えば\(P(i,x)\)を求める問題を解くためには、\(P(i-1,x)\)と\(P(i-1,x-a_i)\)の2つのサブ問題を解く必要があります。
物が\(n\)個あり、その中の最初の\(i\)個だけから選び、重量制限が\(x\)のナップサック問題を考える。この問題の最適値を\(P(i,x)\)とすると、以下の式が成り立つ。
\(\begin{equation} P(i,x)= \begin{cases}P(i-1,x) & (a_i>x) \\ \max\{P(i-1,x),\;P(i-1,x-a_i)+c_i\} & (a_i \leq x) \end{cases} \end{equation}\)
但し\(a_i\)は物\(i\)の重量、\(c_i\)は物\(i\)の満足度
このように問題をサブ問題に分割して考えると
最終的には何個のサブ問題を解けば良いのか
ということが計算量を決めるうえで重要になります。
再帰式の計算時間とは、\(P(i-1,x)\)と\(P(i-1,x-a_i)\)の値がすでに分かっているときに、
\(\begin{equation} P(i,x)= \begin{cases}P(i-1,x) & (a_i>x) \\ \max\{P(i-1,x),\;P(i-1,x-a_i)+c_i\} & (a_i \leq x) \end{cases} \end{equation}\)
で\(P(i,x)\)を計算するのにどれくらい時間がかかるかということです。今回は\(O(1)\)で計算できるので、問題の数について考えていきます。
動的計画法じゃないverの計算量
それではまず最初に動的計画法じゃないverの計算量について考えたいと思います。計算量を考える上で重要な問題の数について考えていきます。
具体例を使って考える
まず分かりやすいように以下の問題について、あの再帰式を使って解くことを考えます。
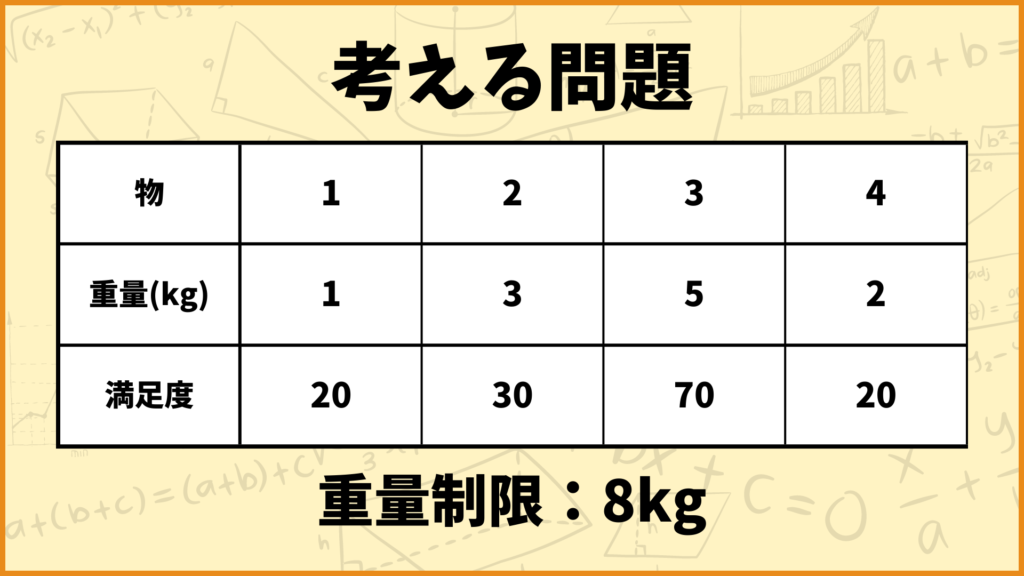
この問題は\(i=4,\;x=8\)のナップサック問題です。それでは一体この問題が最終的に何個の問題に分割されるかを考えてみましょう。
\(a_4=2 \leq 8 = x\)なので\(P(4,8)=\max\{P(3,8),\;P(3,6)+2\}\)と表せます。つまり\(P(4,8)\)を求める問題を\(P(3,8),\;P(3,6)\)を求める2つのサブ問題に分割できました。
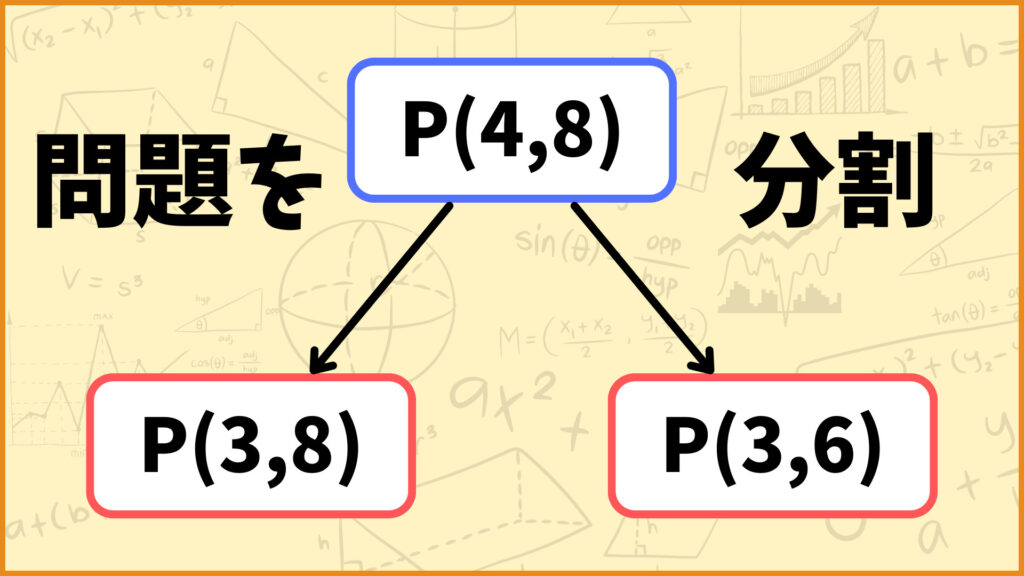
これによって\(i=4\)の問題を\(i=3\)の問題のみで表現することができました。次にこの2つのサブ問題をさらに分割してみましょう。
先ほどと同じようにに考えます。\(a_3=5 \leq 8,\; a_3=5 \leq 6\)なので\(P(3,8)\)は\(P(2,8),\;P(2,3)\)の2つに分割され、\(P(3,6)\)は\(P(2,6),\;P(2,1)\)の2つに分割できます。
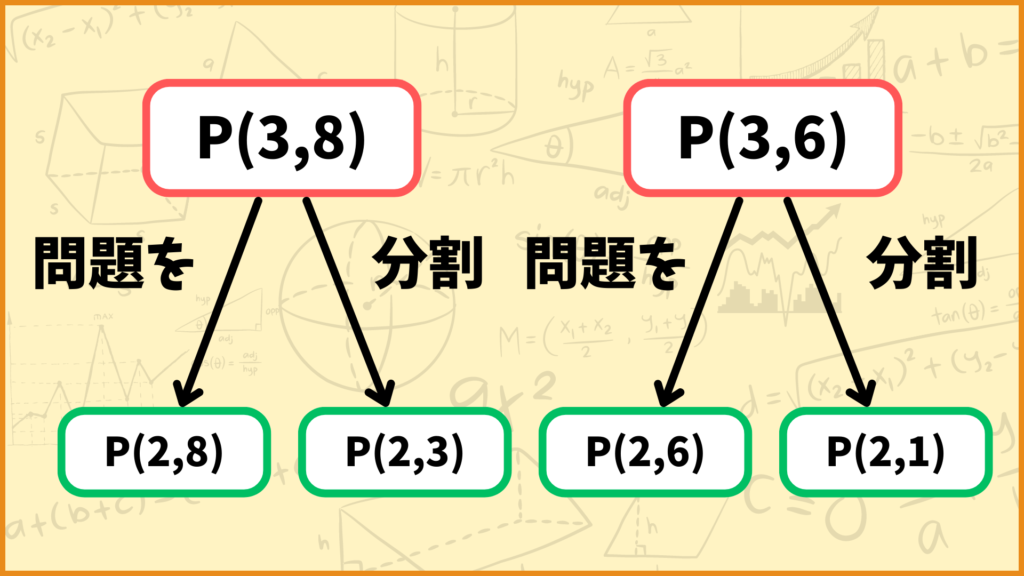
これによって\(i=3\)の問題を\(i=2\)の問題のみで表現することができました。次にこれらのサブ問題をさらに分割してみましょう。
ここからは問題数が多くなってしまうのでまとめて話していきます。\(a_2=3\)なので\(P(2,8),\;P(2,3),\;P(2,6)\)の3つの問題はそれぞれ\(i=1\)の2つの問題に分割できます。
\(P(2,1)\)は\(P(2,1)=P(1,1)\)と表せます。(1つの問題に分割という言い方で合っているんですかね笑)
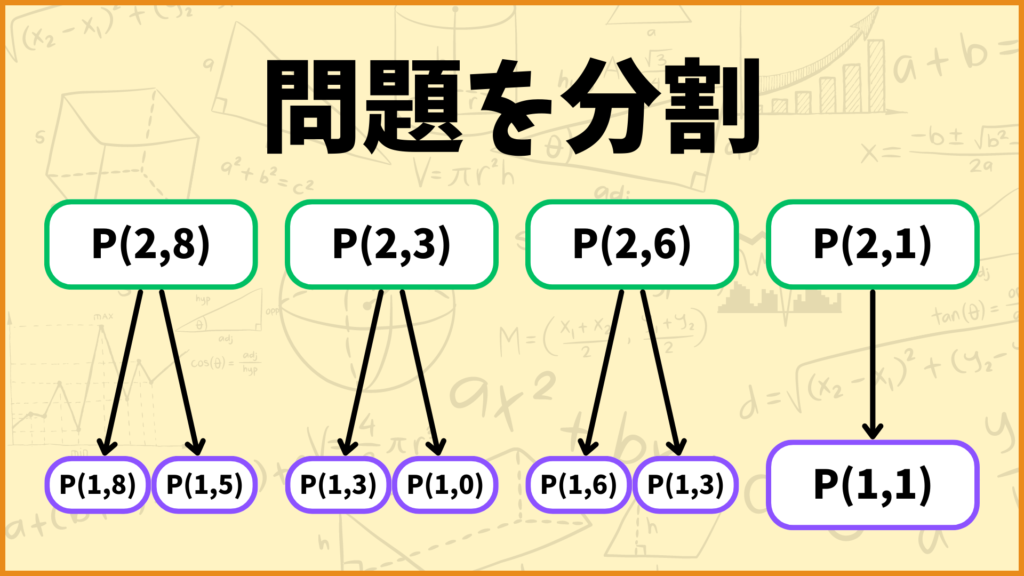
これによって\(i=2\)の問題を\(i=1\)の問題のみで表現することができました。次にこれらのサブ問題をさらに分割してみましょう。
\(a_1=1\)なので\(P(1,0)\)以外の\(P\)は\(i=0\)の問題2つに分割できます。\(P(1,0)\)は\(P(1,0)=P(0,0)\)と表せます。
\(i=0\)のときは物を0個選ぶ、つまり1個も選べないという条件なので、任意の\(x\)に対して\(P(0,x)=0\)となります。
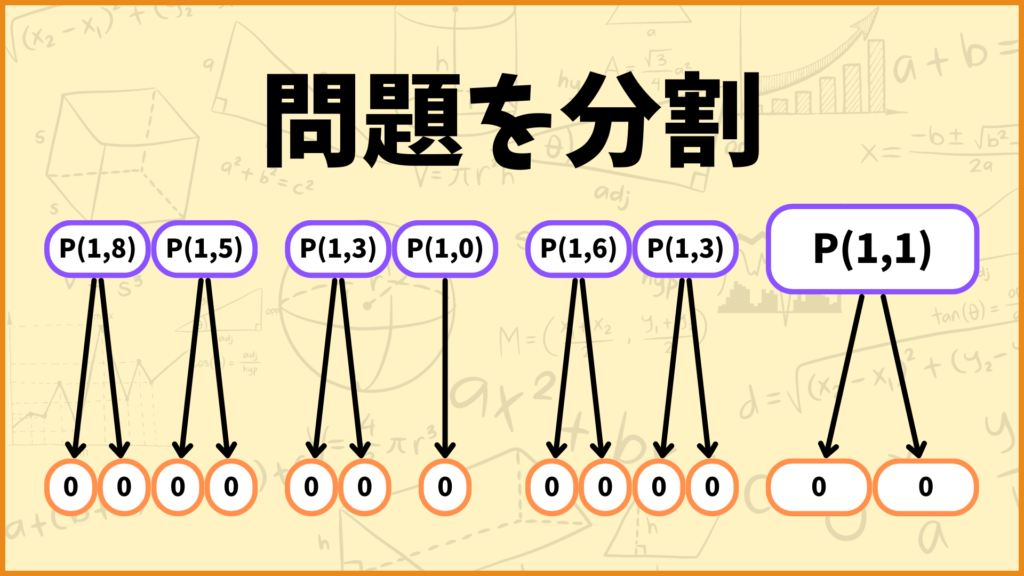
これによって\(i=1\)の問題を\(i=0\)の問題のみで表現することができました。\(P(0,x)=0\) なので分割はこれで終了します。
今回は最終的に13個のサブ問題に分割することができましたが、\(i=4\)の問題は理論上何個までサブ問題に分割できるでしょうか。
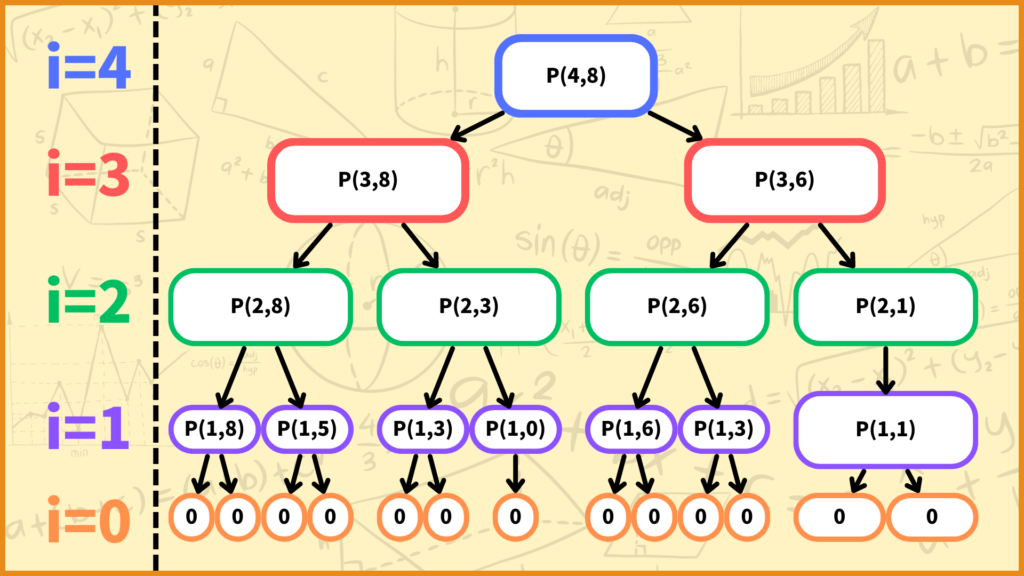
理論的には全ての問題を2つに分割できるパターンが、問題数が一番多くなる場合です。そう考えると\(i=4\)のどんなナップサック問題でも、分割してできるサブ問題の数の最大値は\(2^4=16\)となります。
より一般的に考える
より一般的に物の数が\(n\)個のとき、問題の数は最大でも\(2^n\)個以下になります。
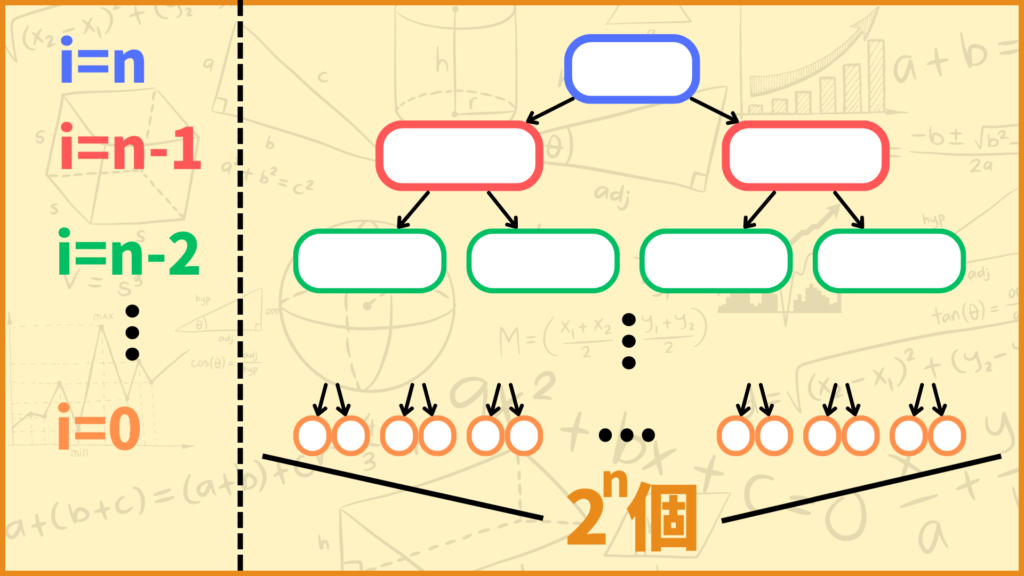
要はそれぞれの物を「選ぶ」か「選ばない」かの2通りあるので、合計で\(2^n\)通りあるということです。
1つ1つの問題を解く時間は\(O(1)\)なので、動的計画法じゃないverの計算量は\(O(2^n)\)になります。
動的計画法verの計算量
動的計画法verの計算量を求めるために、こちらもサブ問題の数を数えてみましょう。動的計画法じゃないverと同じ例を使って考えてみます。
具体例を使って考える
\(i=2\)の問題を\(i=1\)の問題に分割する所をもう一回見てみましょう。
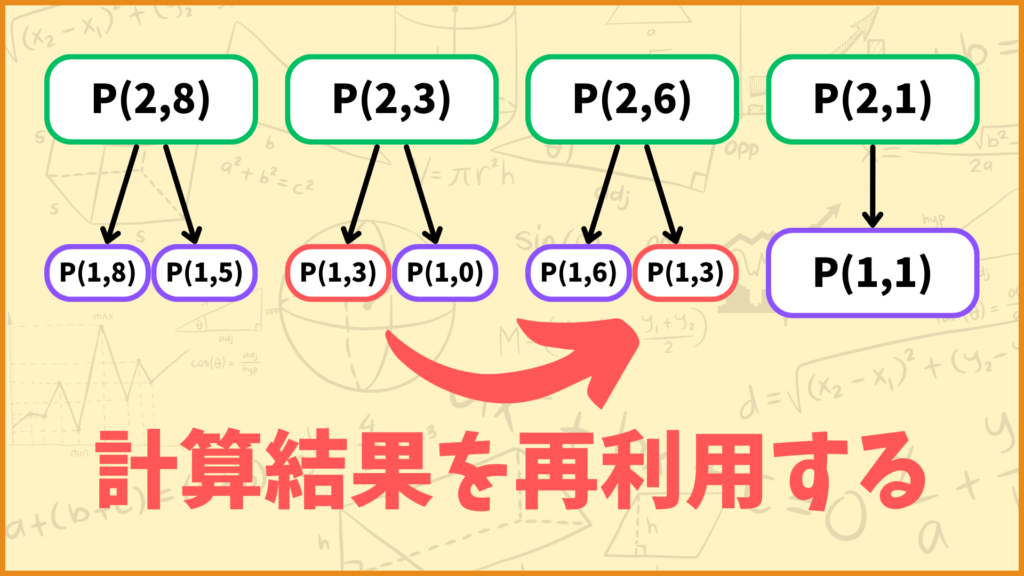
\(P(2,3),\;P(2,6)\)をサブ問題に分割している所を見ると。\(P(1,3)\)が2回登場しています。
同じ計算を2回するのは時間がかかるので、動的計画法では1度計算した結果を再利用します。これによって実際に解かないといけない問題の数は先ほどよりも少なくなるはずです。
それでは動的計画法verの場合は最大で何個のサブ問題を解けば答えが導き出せるのかを考えていきます。結論下の表を全て埋めれば答えが出ます。
(これは動的計画法の計算編の記事で紹介しています。)
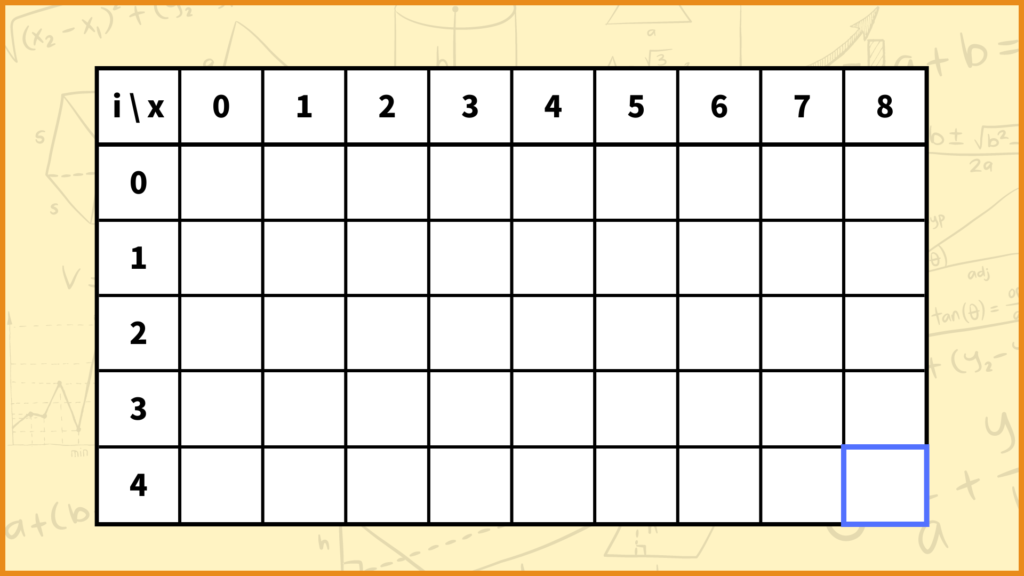
この表についてはこちらの記事で説明しています!
マスの数は\(5×9=45\)個なので、\(i=4,\;x=8\)のどんなナップサック問題も最大45個のサブ問題を解けば元の問題の答えが求まります。
より一般的に考える
より一般に、物の数が\(n\)個、重量制限が\(x\)kgのときの問題数を考えます。結論下の表のマスを全て埋めればOKです。
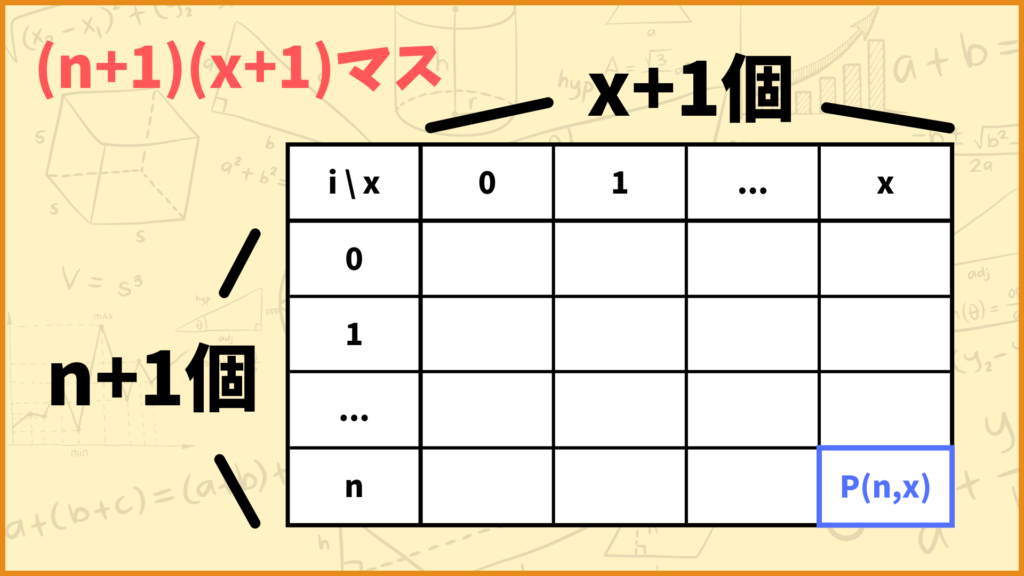
マスの数は\((n+1)(x+1)\)マスなので、解かなきゃいけないサブ問題の最大数は\((n+1)(x+1)\)個となり、\(O(nx)\)と表せます。
ということで動的計画法verの計算量は\(O(nx)\)となります。
厳密に言うと動的計画法は多項式時間では解けません。というのも重量制限\(x\)の入力に必要なデータの長さが\(O(\log_2x)\)となるからです。
(ここら辺の話は自分の勉強不足であまり詳しくないですが、ナップサック問題を動的計画法で解くアルゴリズムは擬多項式時間アルゴリズムと呼ばれるそうです。)
おわりに
いかがでしたか。
今回の記事では動的計画法について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。