- 配送計画問題ってなに?
- 配送計画問題を整数計画問題として定式化したい…
- 配送計画問題をpythonで解きたい…
こんにちは!しゅんです!
今回の記事では配送計画問題を整数計画問題として定式化してpythonで解く方法を解説したいと思います!
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
配送計画問題ってなに?
配送計画問題の簡単な説明
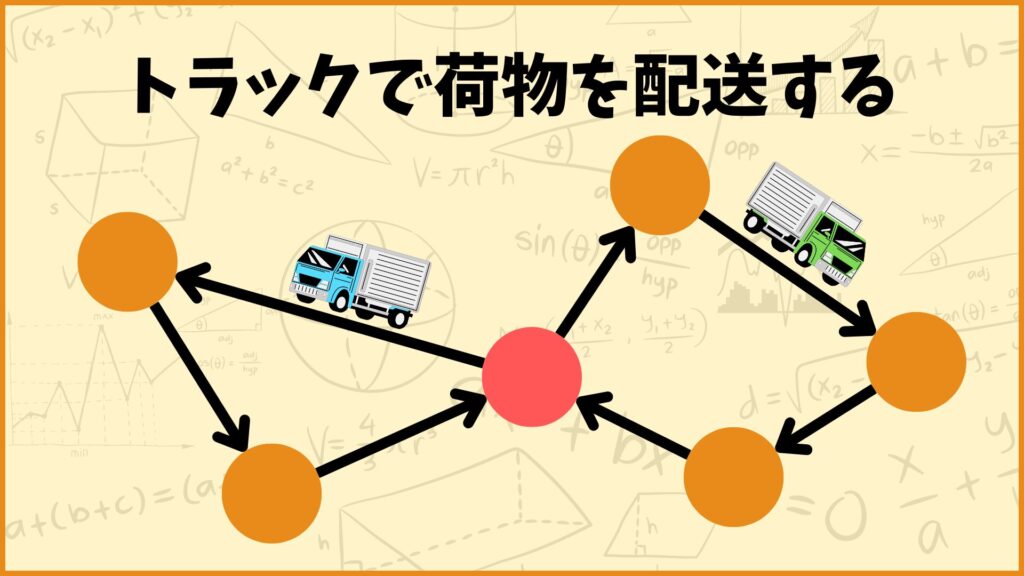
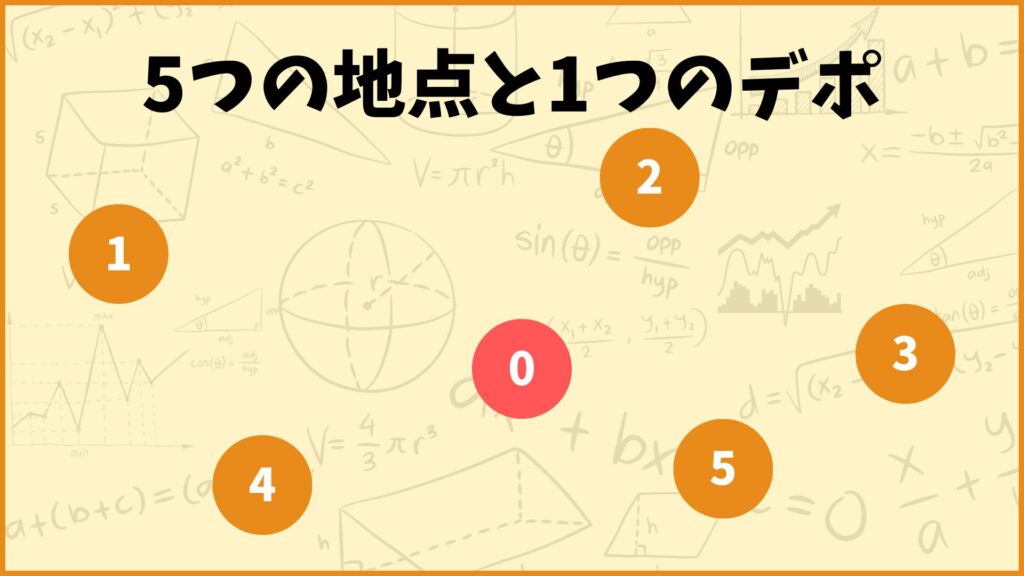
まず最初に配送計画問題(Vehicle Routing Problem, VRP)がどんな問題なのかを簡単に説明します。

例えば上図のように1つの拠点(赤丸)と5つの地点(橙丸)があります。2台のトラックを使って拠点から5つの地点に荷物を配送することを考えます。
このときに、どのトラックも拠点から出発していくつかの地点に荷物を配送してまた拠点に戻ってくるなルートで配送をします。
配送計画問題では拠点のことをデポ(depot)と言ったりします。これ以降はデポと言います。
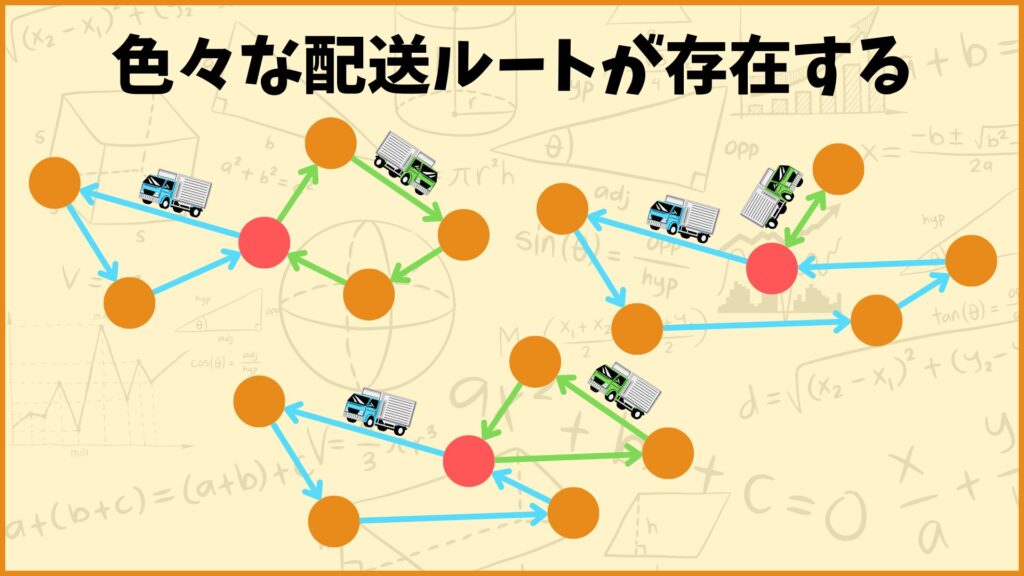
上の条件を満たす配送ルートはたくさんあります。これらの配送ルートの中から一番良い配送ルートを見つける問題が配送計画問題です。
一番良い配送ルートってなに?
それでは次に一番良い配送ルートってどんなルートなのかを説明します。典型的な配送計画問題だと
「車両の移動距離の合計が最小となる配送ルート」
を一番良い配送ルートとします。
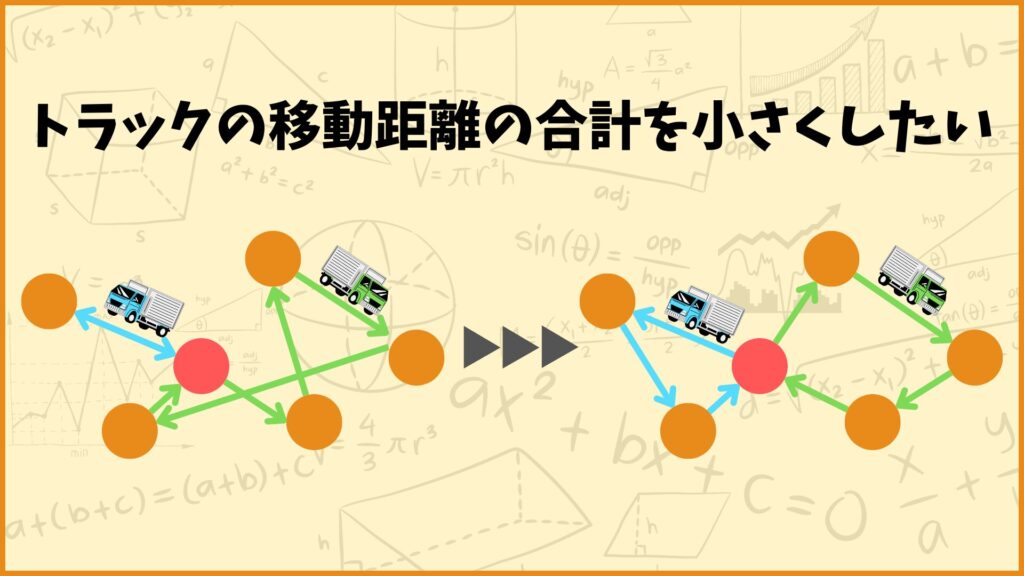
例えば上図で言うと左側の配送ルートよりも右側の配送ルートの方がトラックの移動距離の合計が短いので、右側の方が好ましいみたいな感じです。
問題設定
今回は以下の配送計画問題を整数計画問題として定式化してpythonで解いてみようと思います。
問題設定:
・\(m\) 台の車両で \(n\) 箇所の地点に荷物を配送することを考える。
・各車両はデポから出発していくつかの地点を回ってまたデポに戻ってくる。
・全ての地点はちょうど1回だけ訪れられる。
・地点 \(i\) と地点 \(j\) 間の距離は \(d_{ij}\)(\(d_{ij}=d_{ji}\))。
・地点 \(i\) に配送する荷物の量は \(q_i\)。
・各車両の容量制限は \(Q\)。
目的:
車両の移動距離の合計が最小となるような配送ルートを求める。
この問題のように、車両に容量制限があるタイプの配送計画問題はCapacitiated Vehicle Routing Problem(CVRP)と呼ばれます。
整数計画問題として定式化する
それでは次にこのCVRPを整数計画問題として定式化する方法を説明します。「記号の定義」、「目的関数の設定」、「制約条件の設定」の3つに分けてそれぞれ説明したいと思います。
なお定式化については以下の論文を参考にしました。
Borcinova, Zuzana. “Two models of the capacitated vehicle routing problem.” Croatian Operational Research Review (2017): 463-469.
記号の定義
パラメータ:
\(V\) : (デポを含む)地点の集合 \((|V|=n+1)\)
\(R\) : 車両の集合 \((|R|=m)\)
\(d_{ij}\) : 地点 \(i\) と地点 \(j\) 間の距離
\(q_i\) : 地点 \(i\) に配達する荷物量
\(Q\) : 車両の重量制限
変数:
\(x_{ij}^{r} \in \{0,1\}\) : 車両 \(r\) が地点 \(i\) から地点 \(j\) へ移動するなら1、そうでないなら0を取る0-1変数
パラメータとして \(V,R,d_{ij},q_i,Q\) を設定します。
\(V\) は地点の集合です。例えば10か所の地点に荷物を配送する場合は
\(V = \{0,1,2,…,10\}\)
となります。なお、デポを0とします。
\(R\) は車両の集合です。例えば3台の車両を使う場合は
\(R = \{1,2,3\}\)
となります。
\(d_{ij}\) は地点 \(i\) と地点 \(j\) 間の距離です。例えば地点2と地点5間の距離が4の場合
\(d_{25}=4\)
となります。
\(q_i\) は地点 \(i\) に配送する荷物の量です。例えば地点3に配達する荷物量が4の場合
\(q_3 = 4\)
となります。\(Q\) は車両の重量制限です。例えば最大で20の荷物量を載せることができる場合
\(Q = 20\)
となります。
目的関数の設定
目的関数:
\(\sum\limits_{r \in R}\sum\limits_{i \in V}\sum\limits_{j \in V, i \ne j}d_{ij}x_{ij}^{r}\)
今回の配送計画問題(CVRP)の目的は
「車両の移動距離の合計が最小となる配送ルートを求める」
というものです。
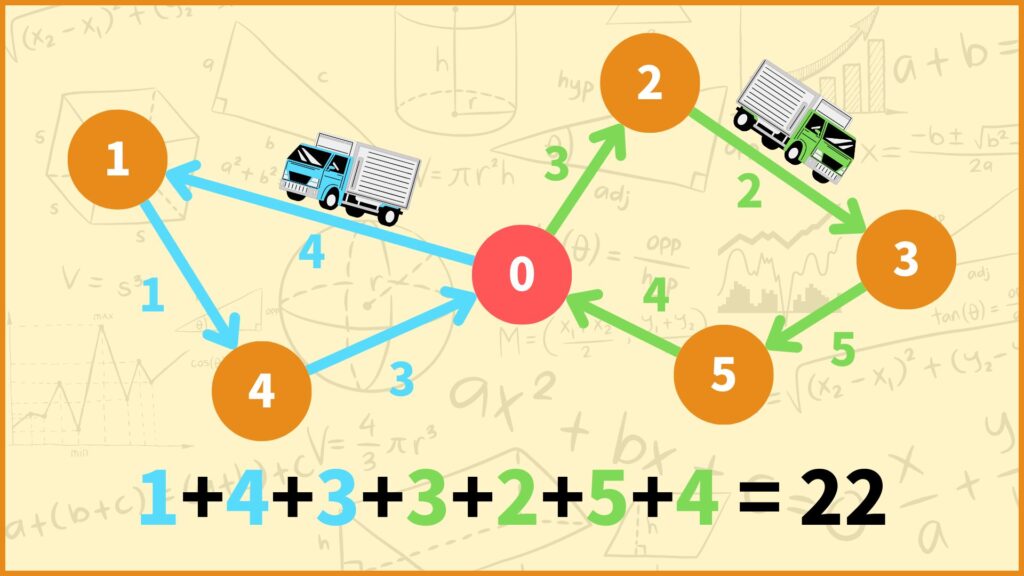
例えば上図の配送ルートを考えます。矢印のそばに書いてある数字が2地点間の距離を表しています。このとき車両の移動距離の合計は
\((1+4+3)+(3+2+5+4)=22\)
となります。一方で青いトラックを車両1、緑のトラックを車両2とすれば各変数の値は
\(x_{01}^1=x_{14}^1=x_{40}^1=x_{02}^2=x_{23}^2=x_{35}^2=x_{50}^2=1\)
となり、その他の変数の値は0となります。従って今紹介した目的関数値は
\(\sum\limits_{r \in R}\sum\limits_{i \in V}\sum\limits_{j \in V, i \ne j}d_{ij}x_{ij}^{r}\)
\(=d_{01}x_{01}^1+d_{14}x_{14}^1+d_{40}x_{40}^1+d_{02}x_{02}^2+d_{23}x_{23}^2+d_{35}x_{35}^2+d_{50}x_{50}^2\)
\(=1+4+3+3+2+5+4=22\)
となり、車両の移動距離の合計と一致します。今回はこれが最小となる配送ルートを求めたいので、この目的関数を最小化する整数計画問題を作ります。
目的関数(最小化):
\(\sum\limits_{r \in R}\sum\limits_{i \in V}\sum\limits_{j \in V, i \ne j}d_{ij}x_{ij}^{r}\)
制約条件の設定
制約条件:
\(\sum\limits_{r \in R}\sum\limits_{i \in V, i \ne j}x_{ij}^r = 1\;\; (\forall j \in V\backslash\{0\})\)
\(\sum\limits_{j \in V \backslash \{0\}}x_{0j}^r = 1\;\; (\forall r \in R)\)
\(\sum\limits_{i \in V, i \ne j}x_{ij}^r = \sum\limits_{k \in V, j \ne k}x_{jk}^r\;\; (\forall j \in V, \forall r \in R)\)
\(\sum\limits_{i \in V}\sum\limits_{j \in V \backslash \{0\}, i \ne j}q_{j}x_{ij}^r \leq Q \;\; (\forall r \in R)\)
\(\sum\limits_{r \in R}\sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij}^r \leq |S|-1 \;\; (\forall S \subseteq V \backslash \{0\},|S| \geq 2)\)
1つずつ説明していきます。
1つ目の制約条件
1つ目の制約条件:
\(\sum\limits_{r \in R}\sum\limits_{i \in V, i \ne j}x_{ij}^r = 1\;\; (\forall j \in V\backslash \{0\})\)
1つ目の制約は
「各地点にはちょうど1回だけ訪れる」
ということを表しています。

例えば地点3についてこの制約条件考えてみましょう。\(j=3\) について考えれば良いので制約式は
\(\sum\limits_{r \in R}\sum\limits_{i \in V, i \ne 3}x_{i3}^r\)
\(= x_{03}^1+x_{13}^1+x_{23}^1+x_{43}^1+x_{53}^1\)
\(+x_{03}^2+x_{13}^2+x_{23}^2+x_{43}^2+x_{53}^2=1\)
これは \(x_{03}^{1},x_{13}^{1},…,x_{53}^{2}\) の中でどれか1つだけが1になるということです。例えば \(x_{23}^{2}=1\) だとしましょう。これは
「車両2が地点2から地点3へ移動する」
ということを表しています。
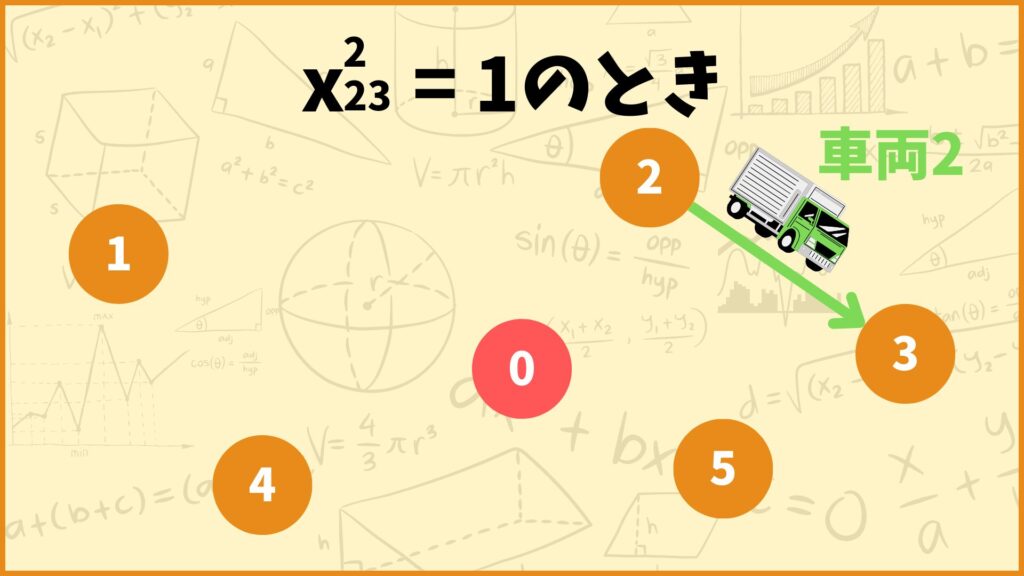
このとき \(x_{03}^1=x_{13}^1=…=x_{53}^2=0\) なので地点3に2回以上訪れることはありません。
この制約が全ての地点について存在すれば良いので \((\forall j \in V\backslash \{0\})\) で全ての地点に対してこの制約を設定しています。
デポに関してはこの制約は必要ありません。
1つ目の制約条件:
\(\sum\limits_{r \in R}\sum\limits_{i \in V, i \ne j}x_{ij}^r = 1\;\; (\forall j \in V\backslash \{0\})\)
2つ目の制約条件
2つ目の制約条件:
\(\sum\limits_{j \in V \backslash \{0\}}x_{0j}^r = 1\;\; (\forall r \in R)\)
2つ目の制約条件は
「車両は必ずデポから出発する」
ということを表しています。
例えば上図の問題例の車両1についてこの制約条件を考えてみましょう。\(r=1\) について考えれば良いので制約式は
\(\sum\limits_{j \in V \backslash \{0\}}x_{0j}^1=x_{01}^1+x_{02}^1+x_{03}^1+x_{04}^1+x_{05}^1=1\)
となります。これは \(x_{01}^1,x_{02}^1,…,x_{05}^1\) のどれか1つが必ず1になるということを表しています。
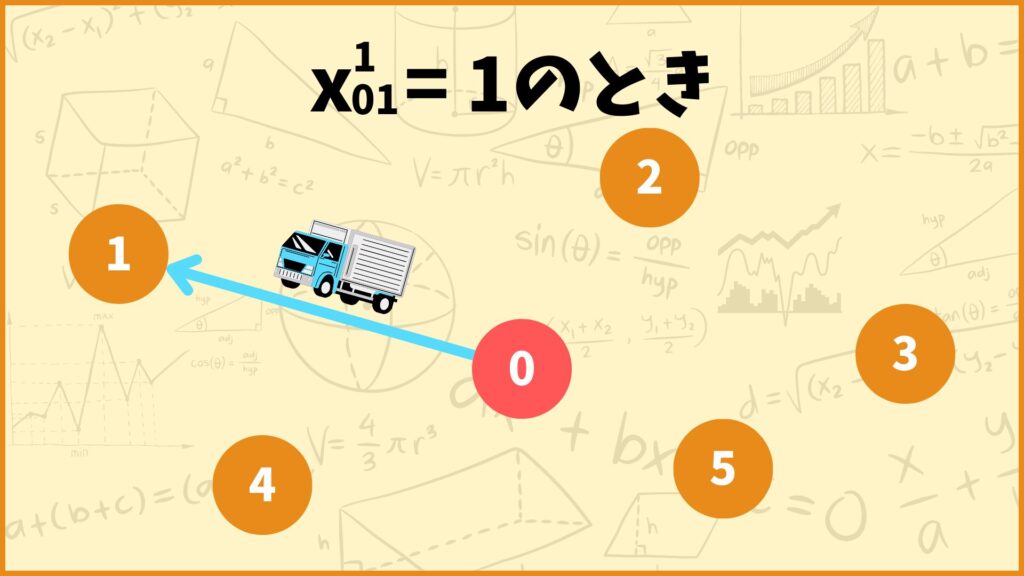
例えば \(x_{01}^1=1\) とします。これは
「車両1がデポから地点1へ移動する」
ということを表しています。このとき \(x_{02}^1=x_{03}^1=x_{04}^1=x_{05}^1=0\) になるのでこれ以上車両1がデポから出発することはありません。
この制約が全ての車両について存在すれば良いので \((\forall r \in R)\) で全ての車両に対してこの制約を設定しています。
2つ目の制約条件:
\(\sum\limits_{j \in V \backslash \{0\}}x_{0j}^r = 1\;\; (\forall r \in R)\)
3つ目の制約条件
3つ目の制約条件:
\(\sum\limits_{i \in V, i \ne j}x_{ij}^r = \sum\limits_{k \in V, j \ne k}x_{jk}^r\;\; (\forall j \in V, \forall r \in R)\)
3つ目の制約条件は
「ある地点に訪れる回数とその地点から出発する回数が一致する」
ということを表しています。

車両2、地点3についてこの制約条件を考えてみましょう。\(r=2,j = 3\)について考えれば良いので制約式は
\((\text{左辺})=\sum\limits_{i \in V, i \ne 3}x_{i3}^2 = x_{03}^2+x_{13}^2+x_{23}^2+x_{43}^2+x_{53}^2\)
\((\text{右辺})=\sum\limits_{k \in V, k \ne 3}x_{3k}^2 = x_{30}^2+x_{31}^2+x_{32}^2+x_{34}^2+x_{35}^2\)
となります。
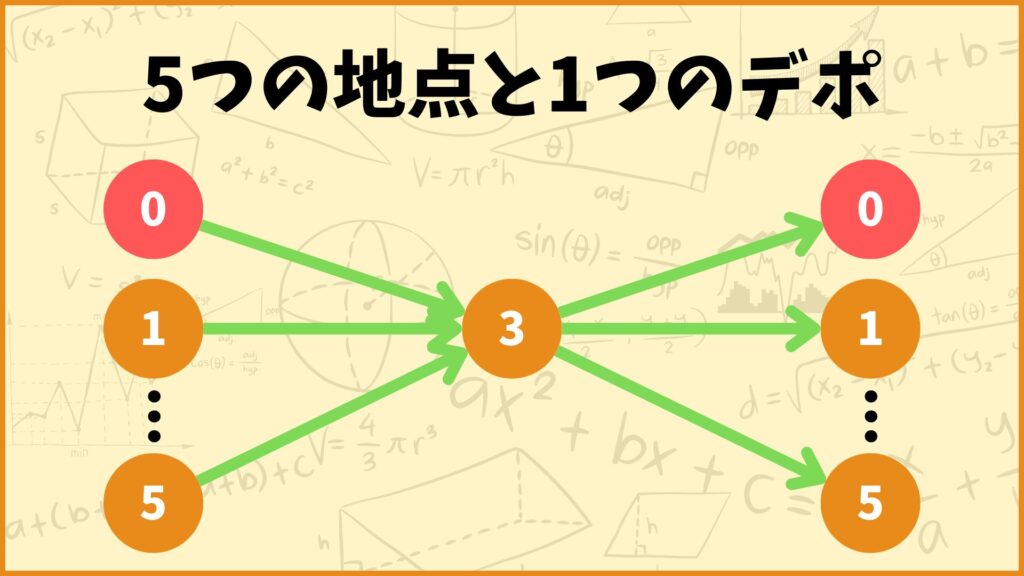
この制約のイメージとしては上図の矢印に関して、3に向かう矢印の本数と3から出る矢印が一致するという感じです。
制約式1から左辺は0か1しか取らないことが分かります。また左辺が0であれば右辺も0、左辺が1であれば右辺も1を取ります。従ってこの式は
「車両2が地点3に訪れるなら車両2は地点3から別の地点へ移動する」
「車両2が地点3に訪れないなら車両2は地点3から別の地点へ移動しない」
と言うことを表しています。
例えば\(x_{23}^2=x_{35}^2=1\)とします。これは
「車両2が地点2→地点3→地点5の順番で配達する」
ということを表しています。
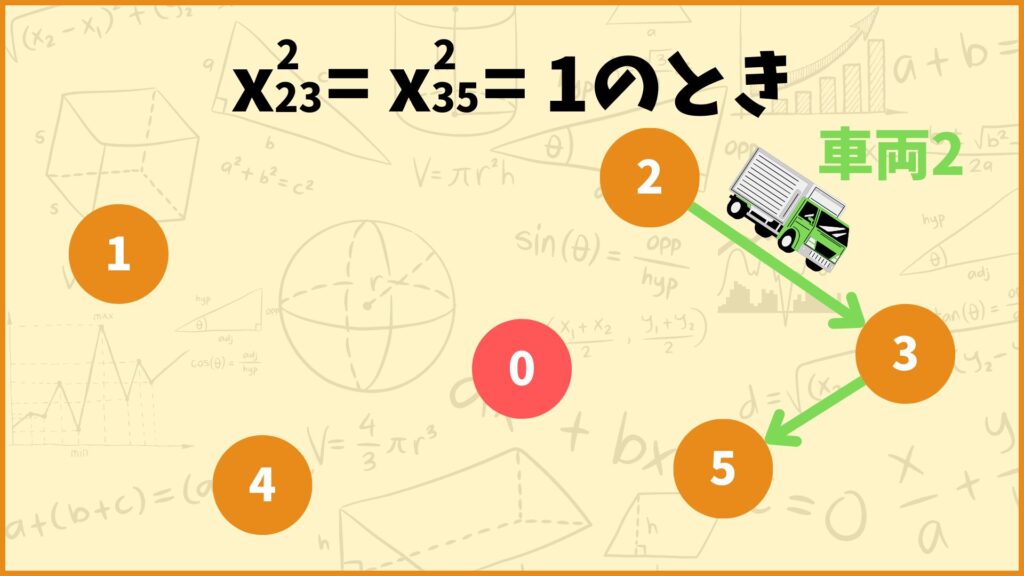
このとき
\(x_{03}^2=x_{13}^2=x_{43}^2=x_{53}^2=0\)
\(x_{30}^2=x_{31}^2=x_{32}^2=x_{34}^2=0\)
となるのでこれ以上車両2が地点3に向かったり、地点3から出発したりすることはできません。
この制約が全ての地点と全ての車両について存在すれば良いので \((\forall j \in V, \forall r \in R)\) で全ての地点と全ての車両に対してこの制約を設定しています。
3つ目の制約条件:
\(\sum\limits_{i \in V, i \ne j}x_{ij}^r = \sum\limits_{k \in V, j \ne k}x_{jk}^r\;\; (\forall j \in V, \forall r \in R)\)
4つ目の制約条件
4つ目の制約条件:
\(\sum\limits_{i \in V}\sum\limits_{j \in V \backslash \{0\}, i \ne j}q_{j}x_{ij}^r \leq Q \;\; (\forall r \in R)\)
4つ目の制約条件は
「車両に積む荷物量は容量制限を超えない」
ということを表しています。
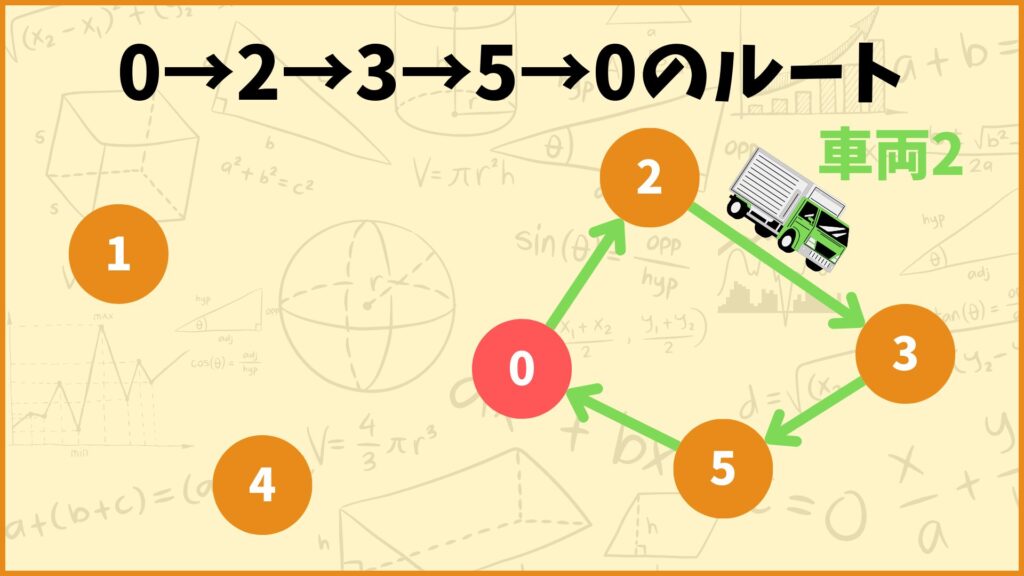
例えば上図のように車両2が0→2→3→5→0のルートで配送する場合についてこの制約条件を考えてみましょう。\(r=2,x_{02}^2=x_{23}^2=x_{35}^2=x_{50}^2=1\)について考えれば良いので制約式は
\(\sum\limits_{i \in V}\sum\limits_{j \in V \backslash \{0\}, i \ne j}q_{j}x_{ij}^2\)
\( = q_2x_{02}^2+q_3x_{23}^2+q_5x_{35}^2 = q_2+q_3+q_5\leq Q\)
となります。\(q_2,q_3,q_5\)はそれぞれ地点2,3,5に届ける荷物量を表しています。その合計が容量制限Qを超えないというのがこの式が表していることです。
この制約が全ての車両について存在すれば良いので\((\forall r \in R)\)で全ての地点と全てのトラックに対してこの制約を設定しています。
4つ目の制約条件:
\(\sum\limits_{i \in V}\sum\limits_{j \in V \backslash \{0\}, i \ne j}q_{j}x_{ij}^r \leq Q \;\; (\forall r \in R)\)
5つ目の制約条件
5つ目の制約条件:
\(\sum\limits_{r \in R}\sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij}^r \leq |S|-1 \;\; (\forall S \subseteq V \backslash \{0\},|S| \geq 2)\)
5つ目の制約は部分巡回路除去制約です。これは第5章で詳しく解説します。
整数計画問題としてまとめる
以上のことを踏まえて整数計画問題として定式化しましょう。
パラメータ:
\(V\) : (デポを含む)地点の集合\((|V|=n+1)\)
\(R\) : 車両の集合\((|R|=m)\)
\(d_{ij}\) : 地点\(i\)と地点\(j\)間の距離
\(q_i\) : 地点\(i\)に配達する荷物量
\(Q\) : 車両の重量制限
変数:
\(x_{ij}^{r} \in \{0,1\}\) : 車両\(r\)が地点\(i\)から地点\(j\)へ移動するなら1、そうでないなら0を取る0-1変数
目的関数(最小化):
\(\sum\limits_{r \in R}\sum\limits_{i \in V}\sum\limits_{j \in V, i \ne j}d_{ij}x_{ij}^{r}\)
制約条件:
\(\sum\limits_{r \in R}\sum\limits_{i \in V, i \ne j}x_{ij}^r = 1\;\; (\forall j \in V\backslash\{0\})\)
\(\sum\limits_{j \in V \backslash \{0\}}x_{0j}^r = 1\;\; (\forall r \in R)\)
\(\sum\limits_{i \in V, i \ne j}x_{ij}^r = \sum\limits_{k \in V, j \ne k}x_{jk}^r\;\; (\forall j \in V, \forall r \in R)\)
\(\sum\limits_{i \in V}\sum\limits_{j \in V \backslash \{0\}, i \ne j}q_{j}x_{ij}^r \leq Q \;\; (\forall r \in R)\)
\(\sum\limits_{r \in R}\sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij}^r \leq |S|-1 \;\; (\forall S \subseteq V \backslash \{0\},|S| \geq 2)\)
\(x_{ij}^r \in \{0,1\} \;\; (\forall i \in V, \forall j \in V, i \ne j,r \in R)\)
ということで整数計画問題として定式化することができました。
部分巡回路ってなに?
それでは先ほど説明を飛ばした部分巡回路除去制約について説明していきます。今回のようにルートの最適化を考える場合は、部分巡回路というものを考慮する必要があります。
部分巡回路ってなに?
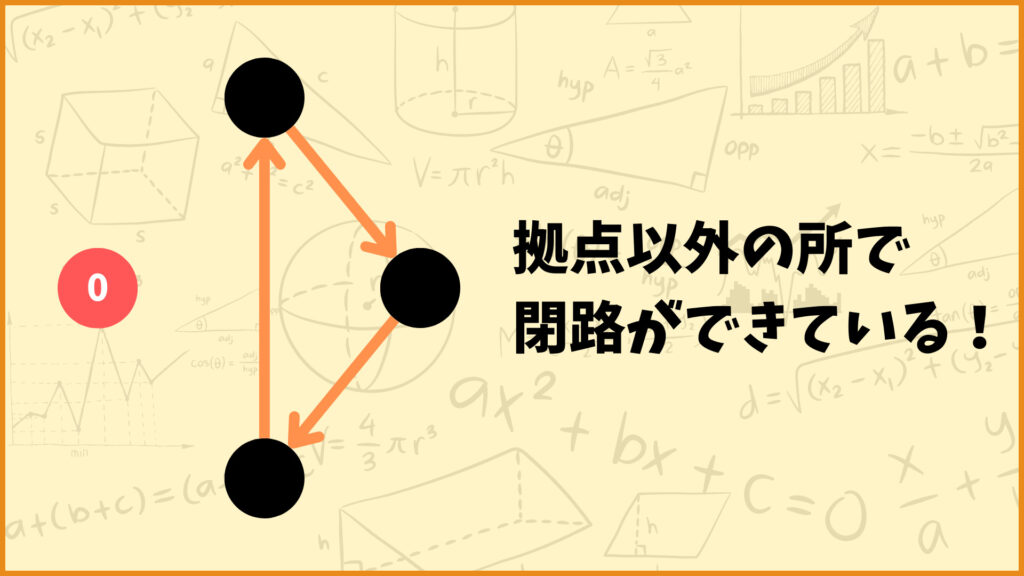
部分巡回路は上図のようなルートです。本来は拠点からスタートして拠点に戻ってくるルートを考えたいのですが、上図は拠点以外の所で閉路ができています。これが部分巡回路です。
配送経路の最適化では部分巡回路はできてほしくないので、除去する必要があります。
どうやって部分巡回路を除去する?
部分巡回路除去制約:
\(\sum\limits_{r \in R}\sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij}^r \leq |S|-1 \;\; (\forall S \subseteq V \backslash \{0\},|S| \geq 2)\)
結論上記の制約で部分巡回路を除去することができます。まず記号の説明をします。\(S\)は拠点を除いた地点の集合\(V\backslash\{0\}\)の部分集合です。例えば\(S = \{1,2\}\)とします。部分巡回路を持たないルートと持つルートをそれぞれ考えてみましょう。
部分巡回路を持たない場合
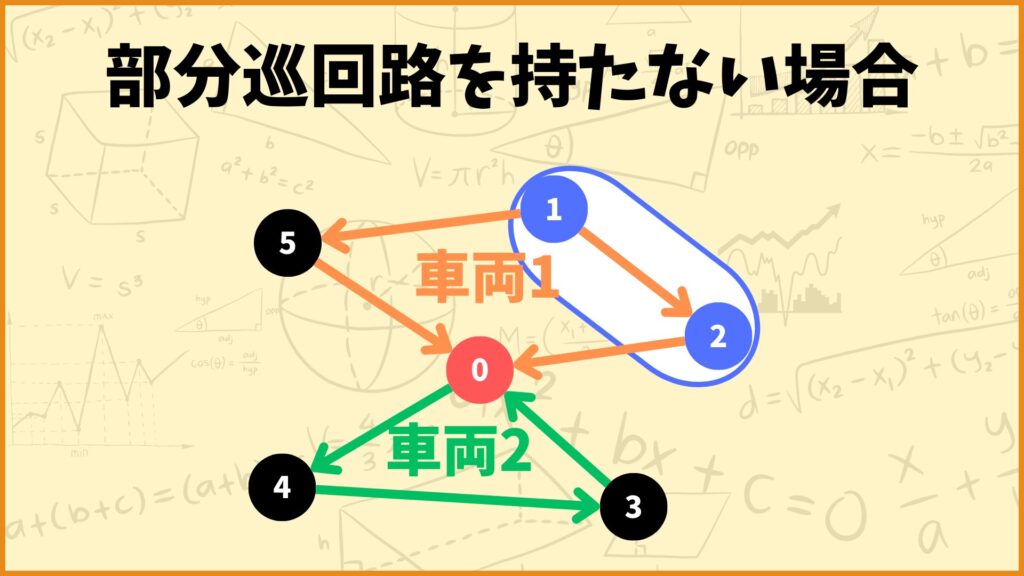
上記のようなルートを考えると、\(x_{12}^1 = 1\)となるので、左辺は
\(\sum\limits_{r \in R}\sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij}^r\)
\( = x_{12}^1 + x_{21}^1 + x_{12}^2 + x_{21}^2\)
\( = x_{12}^1 = 1\)
となり、右辺は
\(|S|-1 = 2 -1 =1\)
となるので制約式を満たします。
部分巡回路を持つ場合
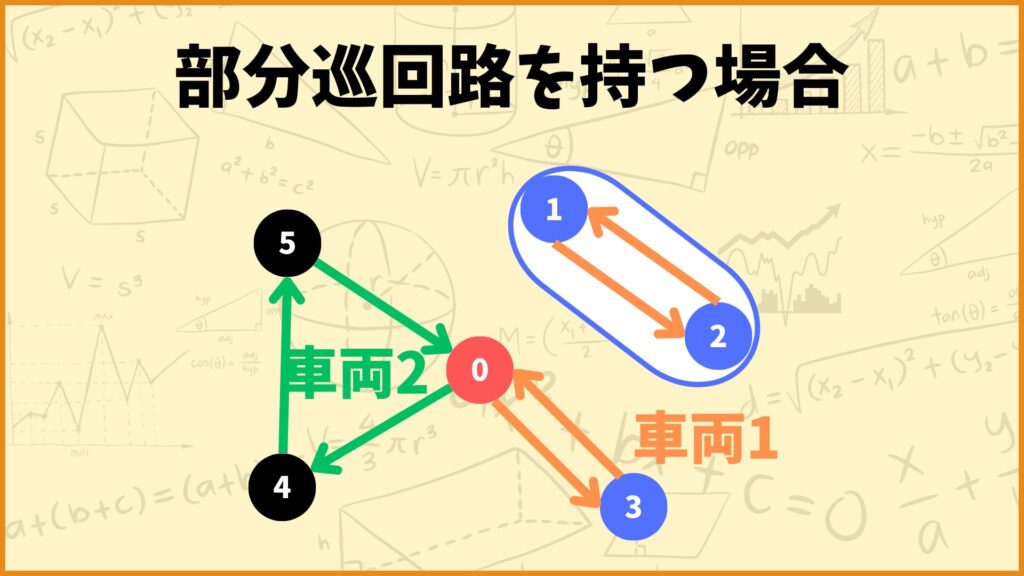
上の例は1つ目から4つ目の制約式を満たすルートですが部分巡回路を持っています。(地点1と地点2の間が部分巡回路です)
このとき\(x_{12}^1 = x_{21}^1 = 1\)となり、制約式の左辺は
\(\sum\limits_{r \in R}\sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij}^r\)
\( = x_{12}^1 + x_{21}^1 + x_{12}^2 + x_{21}^2\)
\( = x_{12}^1 + x_{21}^1 = 2\)
となり、右辺は
\(|S|-1 = 2 -1 =1\)
となるので制約式を満たしません。
\(|S| \geq 2\)な理由を考えてみましょう。まず\(|S|=0\)は明らかに必要ないですね。次に\(|S|=1\)の場合を考えてみましょう。例えば\(S = \{1\}\)とすると左辺は
\(\sum\limits_{r \in R}\sum\limits_{i \in \{1\}}\sum\limits_{j \in \{1\}, i \ne j}x_{ij}^r\)
となります。しかしこれは
\(i = 1,j = 1, i \ne j\)
っていう矛盾した式になってしまいます。そのため\(|S| \geq 2\)となります。
pythonで解いてみた
それでは実際にこの問題をpythonで解いてみましょう。結論以下のプログラムを実行することで問題を解くことができます。
## 事前準備
from pulp import *
import random
from itertools import chain, combinations
random.seed(1) # シード値を1に設定(乱数を固定)
## 記号の設定
n = 6 # 地点数
m = 2 # 車両数
V = [i for i in range(n+1)] # 地点の集合(デポを含む)
V_0 = V[1:] # 地点の集合(デポを除く)
R = [r for r in range(m)] # 車両の集合
q = {i: random.randint(100,500) for i in range(1,n+1)} # 各地点に配送する荷物量
Q = 1200 # 車両の重量制限
# 各地点の座標をランダムに設定
Pos = {}
for i in V_0:
Pos[i] = [random.uniform(0,10), random.uniform(0,10)]
# 地点0の座標を他の地点の平均値に設定
average_x = sum(pos[0] for pos in Pos.values()) / len(Pos)
average_y = sum(pos[1] for pos in Pos.values()) / len(Pos)
Pos[0] = [average_x, average_y]
# # 各地点間の距離を設定
d = {}
for i in V:
for j in V:
d[(i,j)] = ((Pos[i][0] - Pos[j][0])**2 + (Pos[i][1] - Pos[j][1])**2)**(1/2) # ユークリッド距離
# V_0の部分集合を返す関数を定義
def powerset(iterable):
s = list(iterable)
return list(map(list, chain.from_iterable(combinations(s, r) for r in range(len(s)+1))))
# V_0の部分集合を2次元リスト形式で設定
subsets = powerset(V_0)
## 整数計画問題として定式化したものを解く
prob = pulp.LpProblem(sense = LpMinimize) # 問題を最小化に設定
x = LpVariable.dicts("x", [(r, i, j) for r in R for i in V for j in V if i != j], cat="Binary") # 0-1変数を設定
prob += lpSum(d[(i,j)] * x[r,i,j] for r in R for i in V for j in V if i != j) # 目的関数を設定
# 1つ目の制約条件
for j in V_0:
prob += lpSum(x[r,i,j] for r in R for i in V if i != j) == 1
# 2つ目の制約条件
for r in R:
prob += lpSum(x[r,0,j] for j in V_0) == 1
# 3つ目の制約条件
for j in V:
for r in R:
prob += lpSum(x[r,i,j] for i in V if i != j) - lpSum(x[r,j,k] for k in V if j != k) == 0
# 4つ目の制約条件
for r in R:
prob += lpSum(q[j] * x[r,i,j] for i in V for j in V_0 if i != j) <= Q
# 5つ目の制約条件
for S in subsets:
if len(S) >= 2:
prob += lpSum(x[r,i,j] for r in R for i in S for j in S if i != j) <= len(S) - 1
# 計算実行
result = prob.solve()
## 結果の表示
print("解の状態 :",LpStatus[result]) # 解の状態を表示(Optimalと表示されたら最適解が得られている)
print("最適値 ;",prob.objective.value()) # 最適値を表示
# 最適解を表示
for r in R:
for i in V:
for j in V:
if i != j:
if x[r,i,j].value() == 1:
print(f"x_{r}_({i},{j}) =", x[r,i,j].value())
このプログラムを実行したら上の結果が得られました。それではコードが何を表しているのか、そして得られた結果の見方について1つずつ解説していきます。
コードの解説
「事前準備」、「記号の設定」、「整数計画問題として定式化して解く」、「結果の表示」の4つに分けてそれぞれ解説していきます。
事前準備
## 事前準備
from pulp import *
import random
from itertools import chain, combinations
random.seed(1) # シード値を1に設定(乱数を固定)
ここではpulp,random,そしてitertoolsからchain,combinationsをインポートし、毎回同じ乱数が生成されるようにしています。
pulpはpythonで整数計画問題を扱うために使います。
randomはpythonで乱数を扱うために使います。
chain,combinationsはpythonで\(V\backslash\{0\}\)の部分集合\(S\)を作成するために使います。
「random.seed()」でプログラムの実行時に毎回同じ乱数が生成されるようにします。(これ書かないと毎回結果が変わってしまいます。)
記号の設定
## 記号の設定
n = 6 # 地点数
m = 2 # 車両数
V = [i for i in range(n+1)] # 地点の集合(デポを含む)
V_0 = V[1:] # 地点の集合(デポを除く)
R = [r for r in range(m)] # 車両の集合
q = {i: random.randint(100,500) for i in range(1,n+1)} # 各地点に配送する荷物量
Q = 1200 # 車両の重量制限
# 各地点の座標をランダムに設定
Pos = {}
for i in V_0:
Pos[i] = [random.uniform(0,10), random.uniform(0,10)]
# 地点0の座標を他の地点の平均値に設定
average_x = sum(pos[0] for pos in Pos.values()) / len(Pos)
average_y = sum(pos[1] for pos in Pos.values()) / len(Pos)
Pos[0] = [average_x, average_y]
# # 各地点間の距離を設定
d = {}
for i in V:
for j in V:
d[(i,j)] = ((Pos[i][0] - Pos[j][0])**2 + (Pos[i][1] - Pos[j][1])**2)**(1/2) # ユークリッド距離
# V_0の部分集合を返す関数を定義
def powerset(iterable):
s = list(iterable)
return list(map(list, chain.from_iterable(combinations(s, r) for r in range(len(s)+1))))
# V_0の部分集合を2次元リスト形式で設定
subsets = powerset(V_0)
2行目で地点数を設定しています。今回は地点数を6と設定しました。
3行目で車両数を設定しています。今回は車両数を2と設定しました。
4行目でデポを含む地点の集合を設定しています。(0がデポを表します。)
5行目でデポを含まない地点の集合を設定しています。
6行目で車両の集合を設定しています。
7行目で各地点に配送する荷物量を設定しています。荷物量は100以上500以下の整数値をランダムに取ります。
8行目で車両の重量制限を設定しています。今回は1200とします。
10~12行目で各地点(デポを除く)の座標を設定しています。座標は\([0,10]\times[0,10]\)の二次元ユークリッド平面上にランダムに配置されるようにしました。
14~16行目でデポの座標を設定しています。デポの座標は各地点の座標の平均値としています。
18~21行目で2地点間の距離を設定しています。2地点間の距離はユークリッド距離としています。
23~27行目でV_0の部分集合を生成しています。
整数計画問題として定式化して解く
## 整数計画問題として定式化したものを解く
prob = pulp.LpProblem(sense = LpMinimize) # 問題を最小化に設定
x = LpVariable.dicts("x", [(r, i, j) for r in R for i in V for j in V if i != j], cat="Binary") # 0-1変数を設定
prob += lpSum(d[(i,j)] * x[r,i,j] for r in R for i in V for j in V if i != j) # 目的関数を設定
# 1つ目の制約条件
for j in V_0:
prob += lpSum(x[r,i,j] for r in R for i in V if i != j) == 1
# 2つ目の制約条件
for r in R:
prob += lpSum(x[r,0,j] for j in V_0) == 1
# 3つ目の制約条件
for j in V:
for r in R:
prob += lpSum(x[r,i,j] for i in V if i != j) - lpSum(x[r,j,k] for k in V if j != k) == 0
# 4つ目の制約条件
for r in R:
prob += lpSum(q[j] * x[r,i,j] for i in V for j in V_0 if i != j) <= Q
# 5つ目の制約条件
for S in subsets:
if len(S) >= 2:
prob += lpSum(x[r,i,j] for r in R for i in S for j in S if i != j) <= len(S) - 1
# 計算実行
result = prob.solve()
2行目で問題を最小化に設定しています。「sense = LpMaximize」だと目的関数を最大化する問題に設定できます。
3行目で変数を設定しています。「LpVariable.dicts()」は変数をいっぺんに設定できるので変数が多いときに便利です。括弧の中身は左から順に(”変数名”, 添字の集合, 変数の種類)となっています。
変数\(x_{ij}^r\)の添字はそれぞれ\(i,j\)が集合\(V\)、\(r\)が集合\(R\)中の要素なので「for r in R for i in V for j in V」とします。
「cat = “Binary”」で変数を0-1変数に設定しています。連続変数にしたければ「cat = “Continuous”」とします。
4行目で目的関数
\(\sum\limits_{r \in R}\sum\limits_{i \in V}\sum\limits_{j \in V, i \ne j}d_{ij}x_{ij}^{r}\)
を設定しています。pulpで\(\sum\)は「lpSum」で表現できます。「x[r,i,j]」と設定することで\(x_{ij}^r\)、「for i in V for j in V for r in R if i != j」と設定することで\(i \in V, j \in V, r \in R, i \ne j\)を表現できます。
6~7行目で1つ目の制約条件
\(\sum\limits_{r \in R}\sum\limits_{i \in V, i \ne j}x_{ij}^r = 1\;\; (\forall j \in V\backslash\{0\})\)
9~10行目で2つ目の制約条件
\(\sum\limits_{j \in V \backslash \{0\}}x_{0j}^r = 1\;\; (\forall r \in R)\)
12~14行目で3つ目の制約条件
\(\sum\limits_{i \in V, i \ne j}x_{ij}^r – \sum\limits_{k \in V, j \ne k}x_{jk}^r = 0\;\; (\forall j \in V, \forall r \in R)\)
16~17行目で4つ目の制約条件
\(\sum\limits_{i \in V}\sum\limits_{j \in V \backslash \{0\}, i \ne j}q_{j}x_{ij}^r \leq Q \;\; (\forall r \in R)\)
19~21行目で5つ目の制約条件
\(\sum\limits_{r \in R}\sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij}^r \leq |S|-1 \;\; (\forall S \subseteq V \backslash \{0\},|S| \geq 2)\)
をそれぞれ設定しています。
23行目で問題を解いています。問題を解くときは「.solve()」でできます。
結果の表示
## 結果の表示
print("解の状態 :",LpStatus[result]) # 解の状態を表示(Optimalと表示されたら最適解が得られている)
print("最適値 ;",prob.objective.value()) # 最適値を表示
# 最適解を表示
for r in R:
for i in V:
for j in V:
if i != j:
if x[r,i,j].value() == 1:
print(f"x_{r}_({i},{j}) =", x[r,i,j].value())
2行目で解の状態を表示しています。Optimalと表示されたら最適解が得られています。
3行目で最適値を表示しています。
5~10行目で最適解を表示しています。値が1の変数だけ表示するようにしています。
結果の解釈

上記のプログラムを実行したら上のような結果が得られました。1つずつ見ていきます。
1行目は解の状態を表しています。Optimalと表示されているので最適解が得られています。
2行目は最適値を表しています。今回の配送計画問題の最適値は29.458…であることが分かりました。
3~10行目は最適解を表しています。これを見ると例えば車両0はデポ→地点3→地点5→地点4→デポの配送ルートであることが分かります。
ただこれだけだとちょっとよく分からないのでこの結果を図示してどんなルートだったかを確かめてみましょう。
結果を図示する
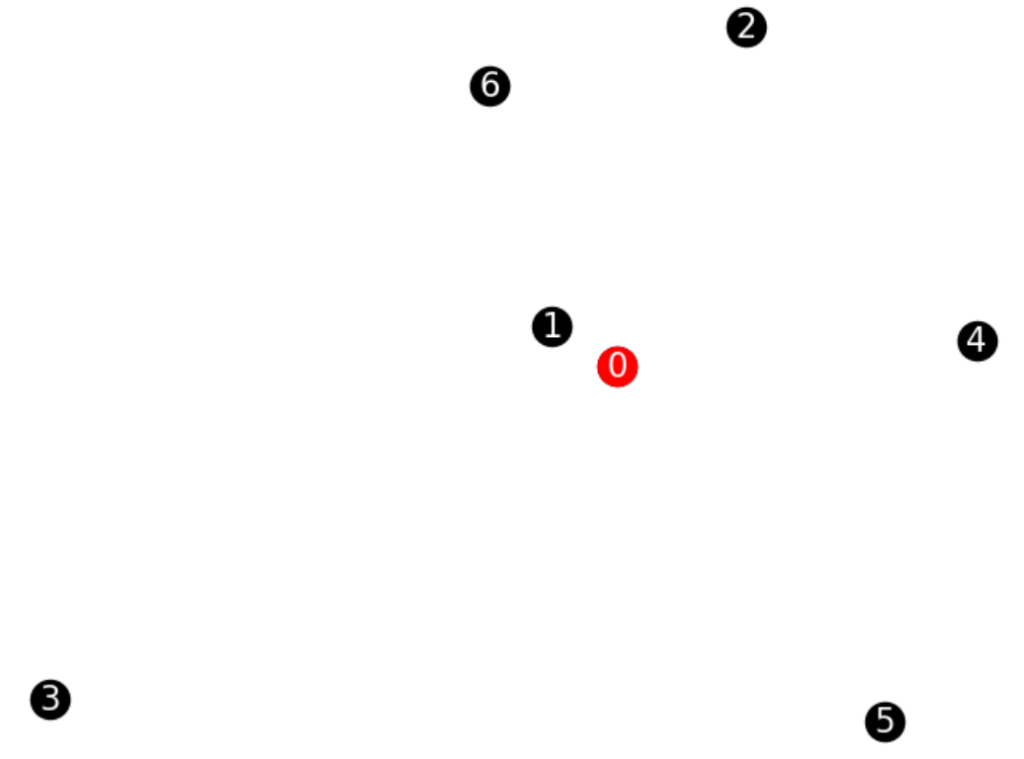
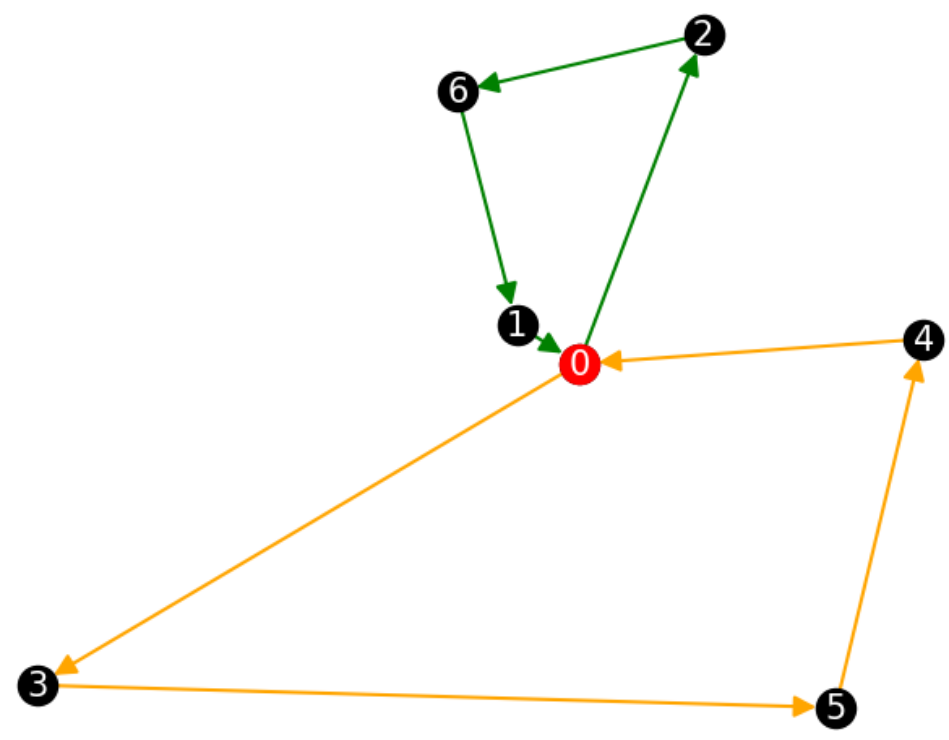
左図が今回の問題例、右図が最適な配送ルートをそれぞれ表しています。0と書かれた赤丸がデポを表しており、それ以外の黒い丸が地点1~6を表しています。先ほどの計算結果と合わせると各車両の配送ルートはそれぞれ
車両0:0→3→5→4→0
車両1:0→2→6→1→0
となります。上の2つの図を表示するコードはそれぞれ以下のようになります。
### 左図を表示するコード
import networkx as nx # networkxをインポート
import matplotlib.pyplot as plt # matplotlibをインポート
# グラフの初期化
G = nx.DiGraph()
# 頂点を追加
for i, pos in Pos.items():
G.add_node(i, pos=pos)
# グラフの描画
pos = nx.get_node_attributes(G, 'pos')
nx.draw(G, pos, with_labels=True, node_color='black', node_size=300,font_size = 15, font_color="white", arrows = False, edgelist=[])
nx.draw_networkx_nodes(G, pos, nodelist=[0], node_color='red', node_size=300)
plt.show()### 右図を表示するコード
import networkx as nx # networkxをインポート
import matplotlib.pyplot as plt # matplotlibをインポート
# グラフの初期化
G = nx.DiGraph()
# 頂点を追加
for v, pos in Pos.items():
G.add_node(v, pos=pos)
# グラフの描画
pos = nx.get_node_attributes(G, 'pos')
nx.draw(G, pos, with_labels=True, node_color='black', node_size=300,font_size = 15, font_color='white')
nx.draw_networkx_nodes(G, pos, nodelist=[0], node_color='red', node_size=300)
# 辺の色を設定
colors = {}
colors[0] = "orange"
colors[1] = "green"
#colors[2] = "blue"
#colors[3] = "purple"
#colors[4] = "salmon"
# 有向辺の描画
edges = [(r,i,j) for r in R for i in V for j in V if i != j if x[r,i,j].value() == 1]
for edge in edges:
r,i,j = edge
nx.draw_networkx_edges(G, pos, edgelist=[(i,j)], edge_color=colors[r], width=1.5, arrowsize=20)
plt.show()
本題ではないのでこれらのコードの説明は省略します。
重量制限を満たしているか確認する
それでは最後に各車両が重量制限を満たしているかを確認してみましょう。各車両に積んだ荷物量を表示するコードは以下のようになります。
weight = [0 for _ in range(len(R))]
for i in V:
for j in V_0:
if i != j:
for r in range(len(R)):
weight[r] += q[j]*x[r,i,j].value()
for r in range(len(R)):
print(f"車両{r}:{weight[r]}")
このコードを実行すると上記の結果が得られました。これを見ると車両0,1どちらもちゃんと重量制限を満たしていることが分かります。
おわりに
いかがでしたか。
今回の記事では配送計画問題について解説していきました。各パラメータを変更すれば異なる結果が得られると思います。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。





