この記事は最近atcoderを始めたぼくがatcoderの問題を通じて勉強したことを書いていく記事です。
atcoderに関する他の記事はこちらから!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学院生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
解きたい問題
長さ\(N\)の正整数列\(A=(A_1,A_2,…,A_N)\)と正整数\(n\)が与えられる。リスト中の2つ要素\(A_i,A_j(i \ne j)\)に対し、\(f(A_i,A_j)\)を「\(A_i\)と\(A_j\)の和が\(n\)以上なら1、そうでなければ0」とする。このとき
\(\sum\limits_{i =1}^{N-1}\sum\limits_{j = i+1}^{N}f(A_i,A_j)\)
を求めよ。\((2 \leq N \leq 3 \times 10^5, 2 \leq n \leq 10^8, 1 \leq A_i \leq 10^8)\)
例えば\(N = 4, A = (1,2,3,4), n = 5\)のとき
\(A_1+A_2=1+2=3 < 5 \Rightarrow f(A_1,A_2)=0\)
\(A_1+A_3=1+3=4 < 5 \Rightarrow f(A_1,A_3)=0\)
\(A_1+A_4=1+4=5 \geq 5 \Rightarrow f(A_1,A_4)=1\)
\(A_2+A_2=2+3=5 \geq 5 \Rightarrow f(A_2,A_3)=1\)
\(A_2+A_2=2+4=6 \geq 5 \Rightarrow f(A_2,A_4)=1\)
\(A_3+A_2=3+4=7 \geq 5 \Rightarrow f(A_3,A_4)=1\)
なので
\(\sum\limits_{i=1}^{N-1}\sum\limits_{j=i+1}^{N}f(A_i,A_j)=4\)
となります。
愚直に全てのパターンを考えると計算量は\(O(N^2)\)になります。\(N\)が小さい場合はこれでよいですが、\(N \leq 3 \times 10^5\)だと時間制限オーバーになってしまうので工夫して計算する必要がありそうです。
コードの解説
N = int(input()) # Nを入力
n = int(input()) # nを入力
A = list(map(int,input().split())) # Aを入力
A.sort() # リストAを小さい順にソートする
count = 0 # 回数の初期設定
left = 0 # リストの左側の初期設定
right = N - 1 # リストの右側の初期設定
while left < right:
if A[left] + A[right] >= n:
count += right - left
right -= 1
else:
left += 1
print(count)
結論上記のコードで問題が解けます。それではなぜこのコードで問題が解けるのかを説明したいと思います。
各パラメータの入力
N = int(input()) # Nを入力
n = int(input()) # nを入力
A = list(map(int,input().split())) # Aを入力
1~3行目で各パラメータを入力しています。ここは本題ではないので説明を飛ばします。
リストをソートする
A.sort() # リストAを小さい順にソートする
4行目ではリストAを小さい順にソートします。例えばA = [1,4,2,3]の場合、上記のコードによってA = [1,2,3,4]と小さい順に並べ替えることができます。
ソートの計算量は\(O(N\text{log}N)\)なので時間制限オーバーはしなさそうです。
条件を満たす回数を数える
count = 0 # 回数の初期設定
left = 0 # リストの左側の初期設定
right = N - 1 # リストの右側の初期設定
while left < right:
if A[left] + A[right] >= n:
count += right - left
right -= 1
else:
left += 1
7~16行目で条件を満たす回数を数えています。下記の具体例を使ってこの部分で何をやっているかを解説したいと思います。
\(N = 7, A = [1,4,5,10,13,16,20], n = 15\)
\(A\)は既に小さい順にソートされているものとします。
初期設定
count = 0 # 回数の初期設定
left = 0 # リストの左側の初期設定
right = N - 1 # リストの右側の初期設定
まず最初にcount,left,rightの3つの値を設定します。これらはそれぞれ
count:条件を満たす回数を数える用
left:リストの左側を指定する用
right:リストの右側を指定する用
となっています。\(N = 7\)なのでrightの値は6となります。これらを何に使うのかはこの後でより詳しく説明します。


全パターンを列挙して上図に書いてみました。これ以降各反復において「未探索な組」を黒色、「条件を満たす組」を橙色、「条件を満たさない組」を緑色で表します。
1回目の反復
while left < right: # left = 0, right = 6
if A[left] + A[right] >= n: # A[left] = 1, A[right] = 20 → A[left]+A[right] >= 15を満たす
count += right - left # count = 6-0 = 6
right -= 1 # right = 6-1 = 5
else:
left += 1
では1回目の反復で何が起こるかを確認してみましょう。このコードではまずleft < rightかどうかを確認します。
left = 0, right = 6
なので条件を満たしていますね。次にA[left]+A[right] >= nかどうかを確認してみましょう。
A[left]+A[right]=1+20=21 >= 15
となるので条件を満たしています。 このときcountにright-left=6を追加しましょう。

この操作が何を表しているかを考えていきます。今\(1+20=21 \geq 15\)が成立しています。さらにリストは小さい順に並んでいます。このことから計算する必要もなく
\(4+20,5+20,10+20,13+20,16+20\)も\(15\)以上になる
ということが分かります。そのためこれらの回数をcountに追加するという訳です。条件を満たすペアは
\((1,20),(4,20),(5,20),(10,20),(13,20),(16,20)\)
で6組ですが、これは大きい方の数を20で固定したときに、小さい方の数はleft(=0)番目の数字からright-1(=5)番目の数字まで条件を満たすということなので、条件を満たすペアの組の数は
\((\text{right}-1)-\text{left} + 1 = \text{right} – \text{left}\)
となります。なのでcountにright-leftを追加します。
重要なのは「計算する必要もなく」6組だと分かるということです。計算する必要がないということは計算量を抑えることができるというわけです。
数え終わったらrightの値を1だけ少なくしましょう。この時点でright=6-1=5となります。この操作は
「大きい方の数が20の場合は数え終わったから大きい方の数字を16として2回目の反復を行う」
ということを表しています。
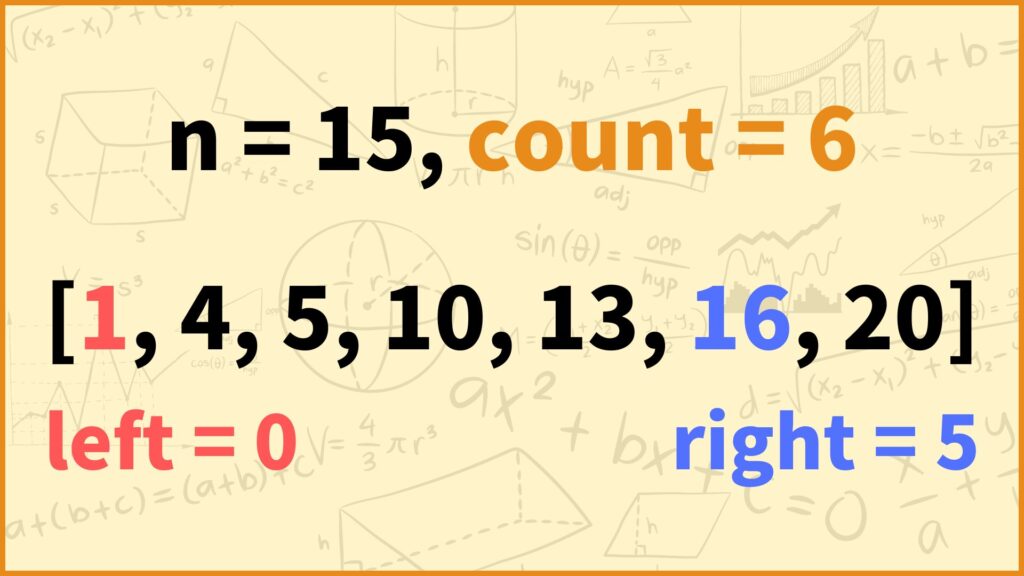

1回目の反復によって上記のようになりました。
2回目の反復
while left < right: # left = 0, right = 5
if A[left] + A[right] >= n: # A[left] = 1, A[right] = 16 → A[left]+A[right] >= 15を満たす
count += right - left # count = 5-0 = 5
right -= 1 # right = 5-1 = 4
else:
left += 1
次に2回目の反復で何が起こるかを確認してみましょう。まずleft < rightかどうかを確認しましょう。
left = 0, right = 5
なので条件を満たしていますね。次にA[left]+A[right] >= nかどうかを確認してみましょう。
A[left]+A[right]=1+16=17 >= 15
となるので条件を満たしています。 このときcountにright-left=5を追加しましょう。

この操作が何を表しているかを考えていきます。今\(1+16=17 \geq 15\)が成立しています。さらにリストは小さい順に並んでいます。このことから計算する必要もなく
\(4+16,5+16,10+16,13+16\)も\(15\)以上になる
ということが分かります。そのためこれらの回数をcountに追加するという訳です。条件を満たすペアは
\((1,16),(4,16),(5,16),(10,16),(13,16)\)
で5組ですが、これは大きい方の数を16で固定したときに、小さい方の数はleft(=0)番目の数字からright-1(=4)番目の数字まで条件を満たすということなので、条件を満たすペアの組の数は
\((\text{right}-1)-\text{left} + 1 = \text{right} – \text{left}\)
となります。なのでcountにright-leftを追加します。
重要なのは「計算する必要もなく」6組だと分かるということです。計算する必要がないということは計算量を抑えることができるというわけです。
数え終わったらrightの値を1だけ少なくしましょう。この時点でright=5-1=4となります。この操作は
「大きい方の数が16の場合は数え終わったから大きい方の数字を13として3回目の反復を行う」
ということを表しています。


2回目の反復によって上記のようになりました。
3回目の反復
while left < right: # left = 0, right = 4
if A[left] + A[right] >= n: # A[left] = 1, A[right] = 13 → A[left]+A[right] >= 15を満たさない
count += right - left
right -= 1
else: # こっち
left += 1 # left = 0+1 = 1
次に3回目の反復で何が起こるかを確認してみましょう。まずleft < rightかどうかを確認しましょう。
left = 0, right = 4
なので条件を満たしていますね。次にA[left]+A[right] >= nかどうかを確認してみましょう。
A[left]+A[right]=1+13=14 < 15
となるので条件を満たしていません。 このときcountにはなにも追加せずleftに1を足しましょう。

この操作が何を表しているかを考えていきます。今\(1+13=14 < 15\)が成立しています。さらにリストは小さい順に並んでいます。このことから計算する必要もなく
\(1+10,1+5,1+4\)も\(15\)未満になる
ということが分かります。この反復では小さい数を1としたときに大きい数がright(=4)番目以下の数字は全部条件を満たさないということが分かりました。
そのためcountには何も足しません。
重要なのは「計算する必要もなく」分かるということです。計算する必要がないということは計算量を抑えることができるというわけです。
そしたらleftの値を1だけ大きくしましょう。この時点でleft=0+1=1となります。この操作は
「小さい方の数が1の場合は数え終わったから小さい方の数字を4として4回目の反復を行う」
ということを表しています。


3回目の反復によって上記のようになりました。
4回目の反復
while left < right: # left = 1, right = 4
if A[left] + A[right] >= n: # A[left] = 4, A[right] = 13 → A[left]+A[right] >= 15を満たす
count += right - left # count = 4-1 = 3
right -= 1 # right = 4-1 = 3
else:
left += 1
次に4回目の反復で何が起こるかを確認してみましょう。まずleft < rightかどうかを確認しましょう。
left = 1, right = 4
なので条件を満たしていますね。次にA[left]+A[right] >= nかどうかを確認してみましょう。
A[left]+A[right]=4+13=17 >= 15
となるので条件を満たしています。 このときcountにright-left=3を追加しましょう。

この操作が何を表しているかを考えていきます。今\(4+13=17 \geq 15\)が成立しています。さらにリストは小さい順に並んでいます。このことから計算する必要もなく
\(5+13,10+13\)も\(15\)以上になる
ということが分かります。そのためこれらの回数をcountに追加するという訳です。条件を満たすペアは
\((4,13),(5,13),(10,13)\)
で3組ですが、これは大きい方の数を13で固定したときに、小さい方の数はleft(=1)番目の数字からright-1(=3)番目の数字まで条件を満たすということなので、条件を満たすペアの組の数は
\((\text{right}-1)-\text{left} + 1 = \text{right} – \text{left}\)
となります。なのでcountにright-leftを追加します。
重要なのは「計算する必要もなく」3組だと分かるということです。計算する必要がないということは計算量を抑えることができるというわけです。
数え終わったらrightの値を1だけ少なくしましょう。この時点でright=4-1=3となります。この操作は
「大きい方の数が13の場合は数え終わったから大きい方の数字を10として5回目の反復を行う」
ということを表しています。


4回目の反復によって上記のようになりました。
5回目の反復
while left < right: # left = 1, right = 3
if A[left] + A[right] >= n: # A[left] = 4, A[right] = 10 → A[left]+A[right] >= 15を満たさない
count += right - left
right -= 1
else: # こっち
left += 1 # left = 1+1 = 2
次に5回目の反復で何が起こるかを確認してみましょう。まずleft < rightかどうかを確認しましょう。
left = 1, right = 3
なので条件を満たしていますね。次にA[left]+A[right] >= nかどうかを確認してみましょう。
A[left]+A[right]=4+10=14 < 15
となるので条件を満たしていません。 このときcountにはなにも追加せずleftに1を足しましょう。

この操作が何を表しているかを考えていきます。今\(4+10=14 < 15\)が成立しています。さらにリストは小さい順に並んでいます。このことから計算する必要もなく
\(4+5\)も\(15\)未満になる
ということが分かります。この反復では小さい数を4としたときに大きい数がright(=3)番目以下の数字は全部条件を満たさないということが分かりました。
そのためcountには何も足しません。
重要なのは「計算する必要もなく」分かるということです。計算する必要がないということは計算量を抑えることができるというわけです。
そしたらleftの値を1だけ大きくしましょう。この時点でleft=1+1=2となります。この操作は
「小さい方の数が4の場合は数え終わったから小さい方の数字を5として6回目の反復を行う」
ということを表しています。


5回目の反復によって上記のようになりました。
6回目の反復
while left < right: # left = 2, right = 3
if A[left] + A[right] >= n: # A[left] = 5, A[right] = 10 → A[left]+A[right] >= 15を満たす
count += right - left # count = 3-2 = 1
right -= 1 # right = 3-1 = 2
else:
left += 1
次に6回目の反復で何が起こるかを確認してみましょう。まずleft < rightかどうかを確認しましょう。
left = 2, right = 3
なので条件を満たしていますね。次にA[left]+A[right] >= nかどうかを確認してみましょう。
A[left]+A[right]=5+10=15 >= 15
となるので条件を満たしています。 このときcountにright-left=1を追加しましょう。
終わったらrightの値を1だけ少なくしましょう。この時点でright=3-1=2となります。この操作は
「大きい方の数が10の場合は数え終わったから大きい方の数字を5として7回目の反復を行う」
ということを表しています。


6回目の反復によって上記のようになりました。
7回目の反復
while left < right: # left = 2, right = 2 →条件を満たさない
if A[left] + A[right] >= n:
count += right - left
right -= 1
else:
left += 1
次に7回目の反復で何が起こるかを確認してみましょう。まずleft < rightかどうかを確認しましょう。
left = 2, right = 2
なので条件を満たしていません。従ってこの時点で反復が終了します。

この時点でちゃんと上図のように未探索のペアが無くなりました。めでたく全てのペアを探索することができました。
条件を満たすペアの数は15組で「count = 15」となっています。
結果を出力する
print(count)
18行目で結果を出力しています。今回の例だとcount=15なので15が出力されます。
計算量は\(O(N\log N)\)
それでは最後にこのプログラムの計算量を考えてみましょう。計算量を考える上で重要な部分が2つあるのでそれぞれについて考えていきます。
ソートの計算量は\(O(N\log N)\)
A.sort() # リストAを小さい順にソートする
ソートの計算量は\(O(N\log N)\)です。
ソートの計算量についてはこちらの記事で解説しています!
組数を数える計算量は\(O(N)\)
count = 0 # 回数の初期設定
left = 0 # リストの左側の初期設定
right = N - 1 # リストの右側の初期設定
while left < right:
if A[left] + A[right] >= n:
count += right - left
right -= 1
else:
left += 1
この部分の計算量は\(O(N)\)です。なぜ計算量が\(O(N)\)なのかを少しだけ考えてみましょう。
初期設定でleft=0, right=N-1とします。 毎回の反復で「leftを1だけ大きくする」or「rightを1だけ小さくする」という操作を行います。すなわち
「毎回の反復でleftとrightの距離が1だけ小さくなる」
ということです。
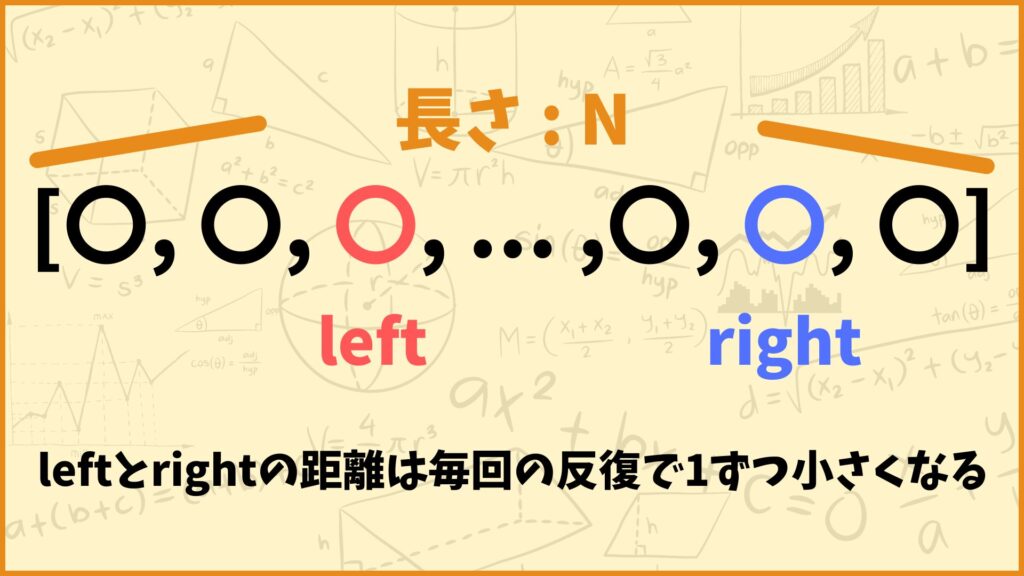
この事実と
・リストの長さがN
・初期設定ではleft=0とright=N-1
・left ≧ rightになったら反復を終了
という事実を合わせると、
「反復回数は\(O(N)\)回となる」
ということが分かります。また各反復で行う計算は\(O(1)\)でできるので、以上をまとめるとこの部分の計算量は\(O(N)\)であることが分かります。
コード全体の計算量は\(O(N\log N)\)
ソートの計算量が\(O(N\log N)\)、組数を数える部分の計算量が\(O(N)\)なのでこのコード全体の計算量は\(O(N\log N)\)となります。
計算量が\(O(N\log N)\)なので\(N \leq 3 \times 10^5\)でも時間制限をオーバーしないで計算できるんですね。
おわりに
いかがでしたか。
今回の記事ではpythonのプログラミングについて解説していきました。
今後もこのようなpythonに関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。