バイトニックシーケンスとフィボナッチ探索とかいうかっこいい専門用語を解説してみた【経営工学を専門にしている大学生の日記】

はじめに

こんにちは！しゅんです！

今回はバイトニックシーケンスとフィボナッチ探索について解説していきます！

なんかめっちゃかっこいい名前ですよね。これらは両方とも数学の用語です。フィボナッチという言葉は聞いたことがあるかもしれませんね。

この記事ではバイトニックシーケンスとフィボナッチ探索の説明と、これら2つにどのようなかかわりがあるのかについて、図を用いてなるべくわかりやすく解説してきます！

それでは解説していきましょう！

普段はNBAのデータ分析をしたりしています。
ぜひこちらの記事も読んでみてください！

もっとみる

このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。

このブログについて

このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます！

ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。

そもそも経営工学とは何なのでしょうか。Wikipediaによると

経営工学（けいえいこうがく、英: engineering management）は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。

引用元 : 経営工学 – Wikipedia

長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。

バイトニックシーケンスってなに？

まずはバイトニックシーケンス(Bitonic Sequence)の説明からしたいと思います。声に出して言いたくなるような専門用語ですね笑

下の図を見てください。

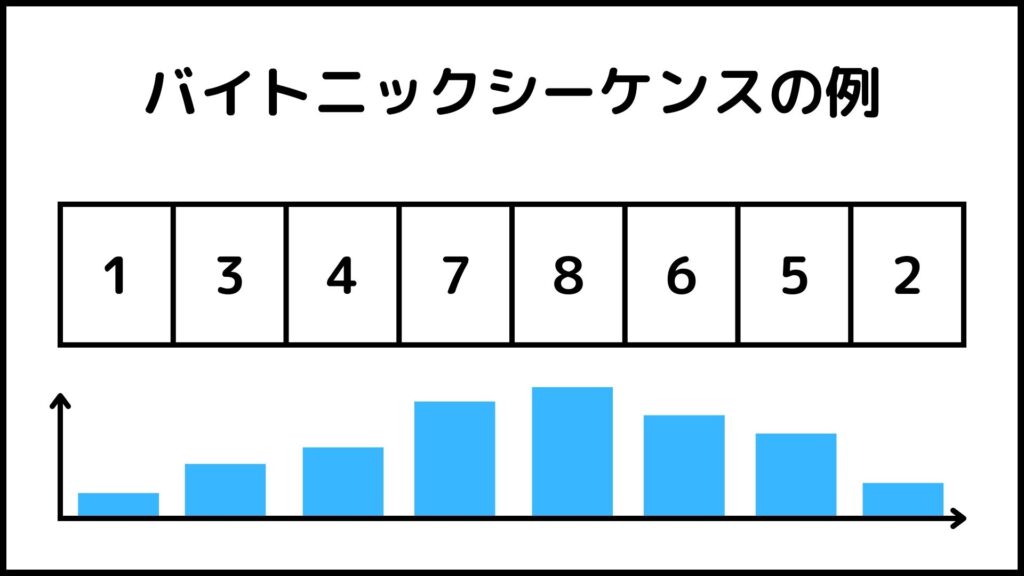
この数字列はバイトニックシーケンスの1つです。この数字列になにか法則性をみつけることができるでしょうか？

正解は数字列の最大値に到達するまでは数字が増加し続け、最大値を超えると数字が減少し続けるという法則性です。この数字列の最大値は8ですが、そこに到達するまで1→3→4→7→8と数字が増え続けていますね。

逆に最大値8を超えると8→6→5→2と数字が減り続けています。グラフで表すと山のようになっているのが分かります。このような数字列のことをバイトニックシーケンスと言います。

より細かい説明は以下のようになります。（難しいので飛ばして大丈夫です）

\(要素数がn個の数字列Aの要素A[i] (1 \leq i \leq n)\)について
\(A[1] \leq A[2] \leq … \leq A[k] \geq … \geq A[n-1] \geq A[n]\)
上記を満たす\(k\)が存在する

例えば下の数字列はバイトニックシーケンスではありません。

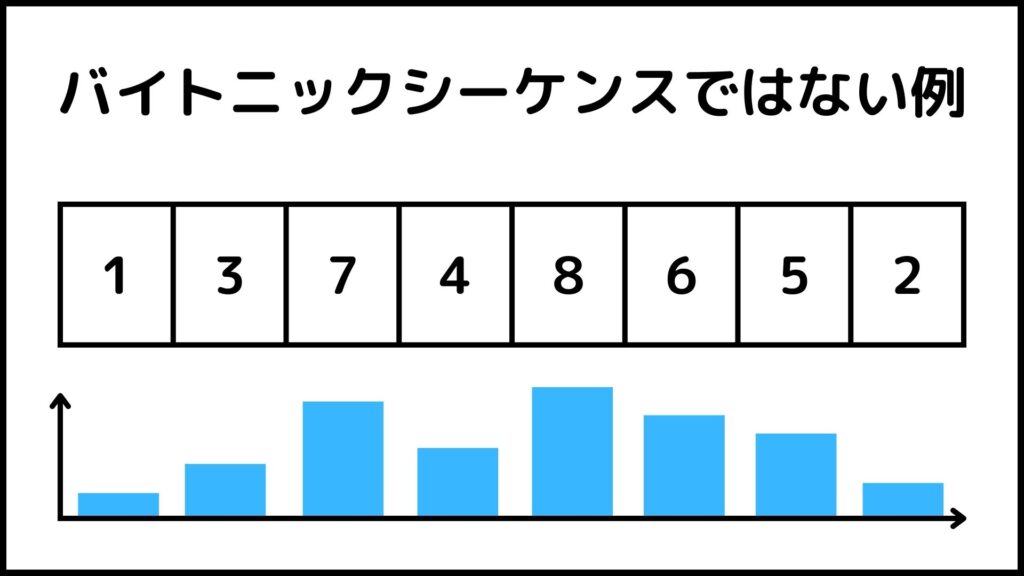
この数字列は山が二か所ありますね。このような数字列はバイトニックシーケンスではないので気を付けてください。

フィボナッチ探索ってなに？

フィボナッチ探索(Fibonacci Search)はフィボナッチ数列を使って数字列から目的の数字を見つけることです。

フィボナッチ数列は非常に有名な数字列なので聞いたことがあるかもしれません。フィボナッチ数列は自然界のいろんなところで表れる数列で、1つ前の数字と2つ前の数字を足したものをどんどん追加していく数列です。

最初とその次の数字は両方1として、それ以降の数字は前と前々の数字を足し算して計算するのがフィボナッチ数列です。

より細かい説明は以下のようになります。（難しいので飛ばして大丈夫です）

\(F_0 = F_1 = 1,\; F_i = F_{i-1} + F_{i-2}\) for \(i \geq 2 \)

バイトニックシーケンスの最大値をフィボナッチ探索で求める

ここまでバイトニックシーケンスとフィボナッチ探索の説明をしていきましたが、ここからはこれら2つにどのような関係があるのかについて説明していきたいと思います。

結論バイトニックシーケンスの最大値を求めるためにフィボナッチ探索が使えるんです。例えば下のバイトニックシーケンスの最大値を求めることを考えます。

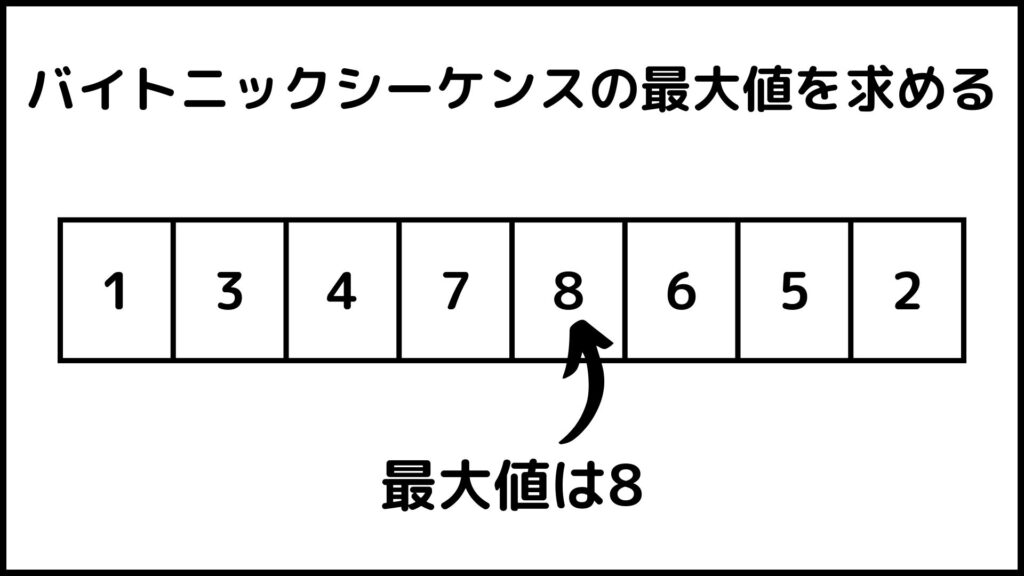
この数字列の最大値は5番目にある8ですね。これをシステマチックに求める方法の1つがフィボナッチ探索です。

手順は以下の通りです。なおフィボナッチ数列を\(F_n\)とし、最大値を求めたいバイトニックシーケンスを\(A\)とします。また\(A\)の要素数を\(n\)とします。

\(F_m \leq nを満たす中で最大のmを選ぶ\)
\(k=0とする\)
\(i = k+F_{m-1}, \; j =k + F_mとする\)
\(A[i] < A[j]ならばk = iとする\)
\(mを1少なくする\)
\(m \geq 2ならばSTEP. 2に戻る\)
\(m \leq 2ならばA[k+1]を返す\)

数式がたくさんあってわけわからなくなったかもしれませんが、具体例を用いて実際に説明していきます。さっきの数字列を用いて最大値を求めていきます。

STEP. 1

まずステップ1の説明からしていきます。

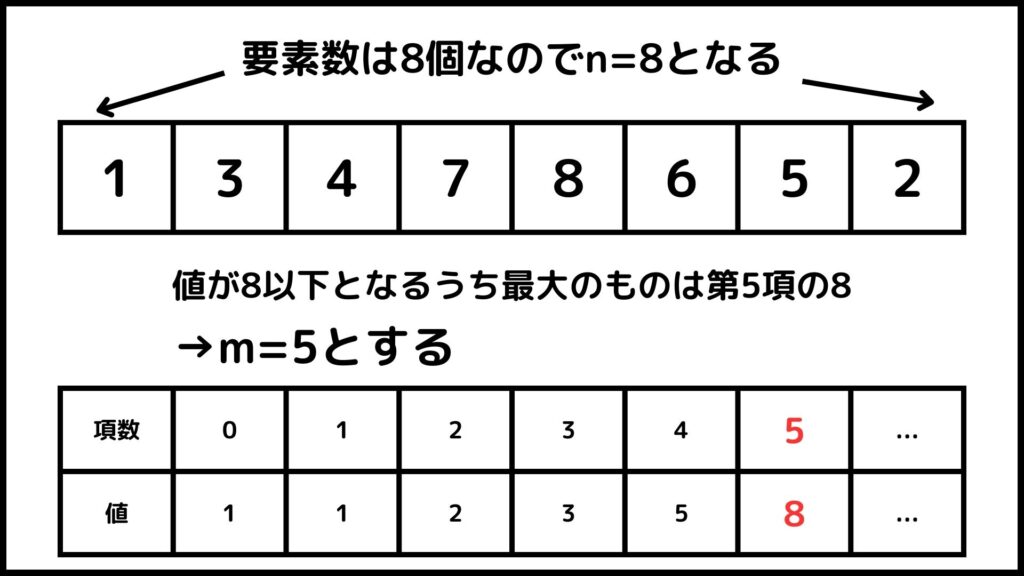
今回のバートニックシーケンスは要素数が8なのでフィボナッチ数列が8以下の中で最大の項を求めます。フィボナッチ数列は第0項から順に1, 1, 2, 3, 5, 8, …となるので、\(m = 5\)となります。

STEP. 2

\(m = 5\)なので\(F_{m-1} = F_4=5, \; F_m = F_5 = 8\)となります。

そのため\(i =0+5=5, \;j=0+8=8\)となります。

STEP. 3

\(A[i] = A[5]=8, \;A[j]=A[8]=2\)となり\(A[i]>A[j]\)となるので\(k=0\)のままです。

STEP. 4

\(m =4\)とします。

STEP. 5

\(m \geq 2\)なのでSTEP. 2に戻ります。

これ以降も同じように計算していきましょう。ここからはかなり省略して説明します。

\(i = 0+F_3=3, \; j = 0+F_4=5\)となります。
\(A[3] < A[5]\)なので\(k = i = 3, \;m=3\)としてSTEP. 2に戻ります。

\(i =2+F_2=4, \; j = 2+F_3=5\)となります。
\(A[4] < A[5]\)なので\(k = i = 4, \; m=2\)としてSTEP.2に戻ります。

\(i=4+F_1=5, \; j= 4+F_2=6\)となります。
\(A[5] > A[6]\)なので\(k=4\)のまま\(m=1\)とします。
この時点で\(m \leq 2\)となったので\(A[k+1] = A[5]=8\)が答えとなります。

このようにして数字列の最大値を求めることができます。手計算でやったので結構大変でしたが、このアルゴリズムをプログラムすれば、めっちゃ長い数字列でも簡単に最大値を計算することができます。