こんにちは!しゅんです!
いきなりですが、下の問題解けますか?
たろう君はA銀行に100万円を預けました。A銀行では年率1%の利子がつきます。ではたろう君が預けた100万円は3年後に何円になっているでしょう?
① 103万円 ② 103万円より多い ③ 103万円より少ない
このような計算は複利計算と呼ばれます。この記事では複利計算がどんな計算なのかについて、上の問題を使って解説していきます。
それではやっていきましょう!
普段は大学数学の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
最初の問題の答え
最初の問題:
たろう君はA銀行に100万円を預けました。A銀行では年率1%の利子がつきます。ではたろう君が預けた100万円は3年後に何円になっているでしょう?
① 103万円 ② 103万円より多い ③ 103万円より少ない
まず最初にさっきの問題の答えから言います。答えは
② 103万円より多い
です。ではなぜこの問題の答えが②なのかを1年後から順を追って解説していきます。
1年後

まず最初に100万円が1年後にいくらになるかを考えてみましょう。問題には年率1%の利子がつくと書いてあるので、預けているお金の1%を毎年ゲットできます。
現在100万円を預けているので、1年間で増えるお金は100万円の1%を計算することで求められます。よって
\((\textbf{1年間で増えるお金}) = 100\text{万円} \times 0.01 = 1\text{万円}\)
となります。
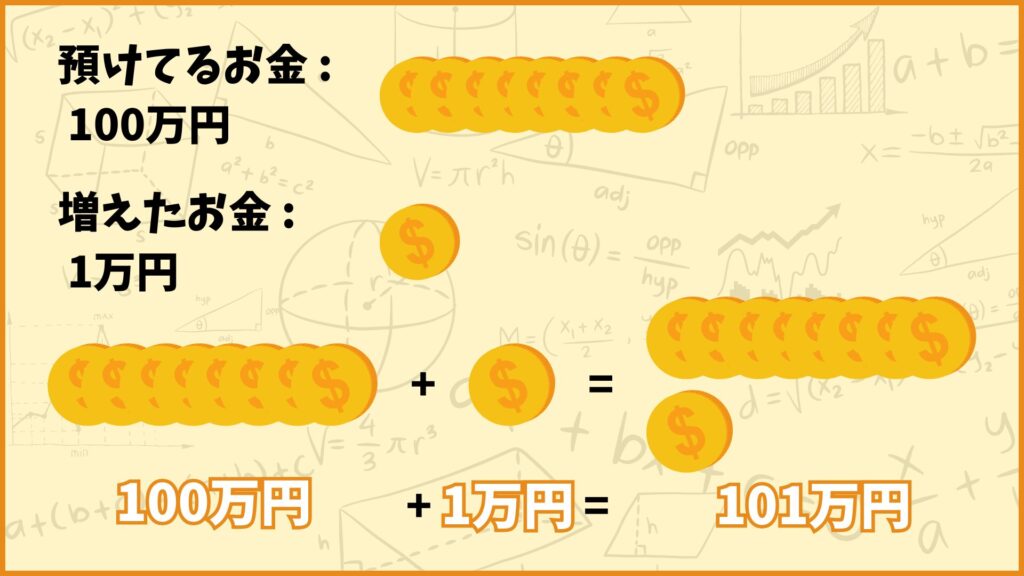
元々預けていた100万円に1年間で増えた1万円足せば1年後のたろう君のお金が求められるので
\((\textbf{1年後のお金}) = 100\text{万円} + 1\text{万円} = 101\text{万円}\)
となります。つまりたろう君が預けた100万円は1年後に101万円になっているということです。
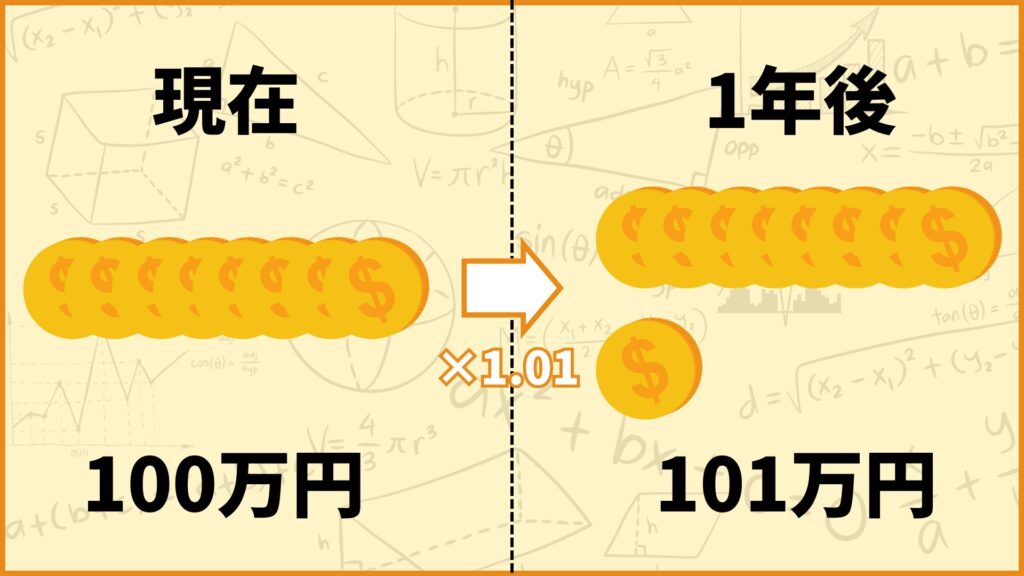
1年間で預けているお金が1%増えるということは、預けていたお金の額が元の額の101%になると考えることもできます。このように考えると
\((\textbf{1年後のお金}) = 100\text{万円} \times 1.01 = 101\text{万円}\)
と計算することもできます。
2年後

次に100万円が2年後にいくらになるかを考えてみましょう。問題には年率1%の利子がつくと書いてあるので、預けているお金の1%を毎年ゲットできます。
さっきの計算で1年後預けているお金が101万円であると計算できました。そのため1年間で増えるお金は101万円の1%を計算することで求められます。よって
\((\textbf{1年間で増えるお金}) = 101\text{万円} \times 0.01 = 1\text{万}\text100{円}\)
となります。
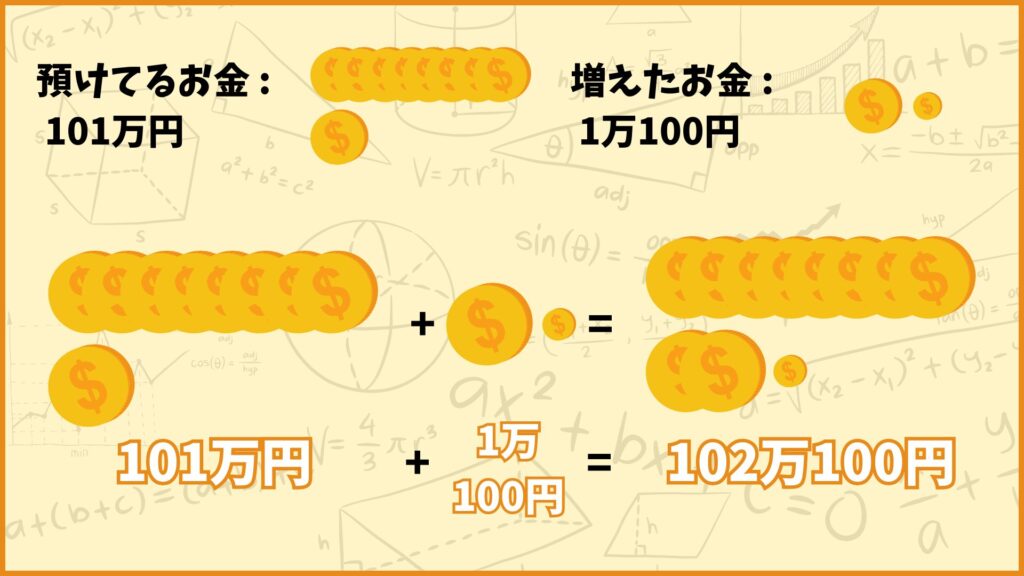
預けていた101万円に1年間で増えた1万100円足せば2年後のたろう君のお金が求められるので
\((\textbf{2年後のお金}) = 101\text{万円} + 1\text{万}100\text{円} = 102\text{万}100\text{円}\)
となります。つまりたろう君が預けた100万円は2年後に102万100円になっているということです。
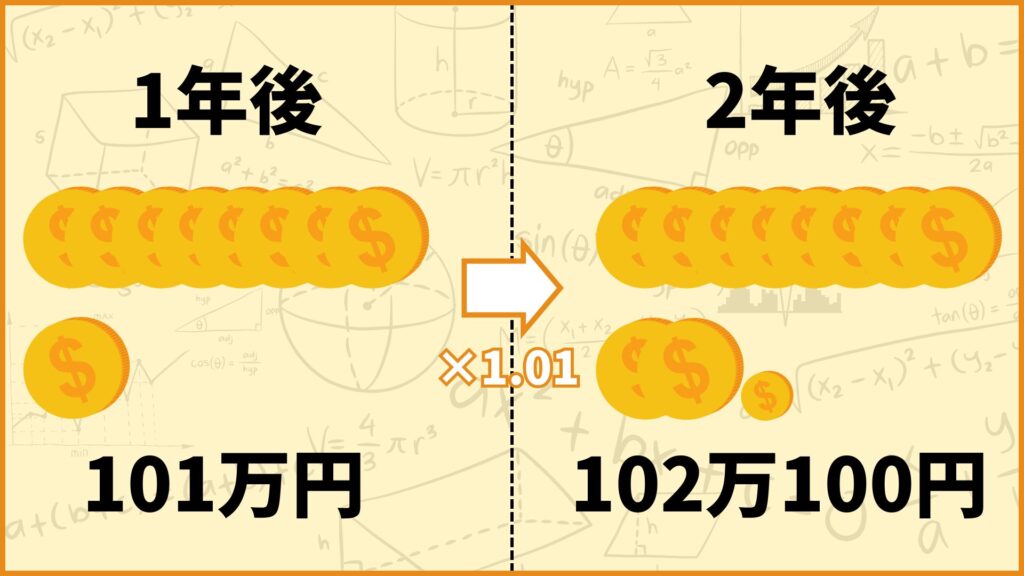
1年間で預けているお金が1%増えるということは、預けていたお金の額が元の額の101%になると考えることもできます。このように考えると
\((\textbf{2年後のお金}) = 101\text{万円} \times 1.01 = 102\text{万}100\text{円}\)
と計算することもできます。
3年後

最後に100万円が3年後にいくらになるかを考えてみましょう。問題には年率1%の利子がつくと書いてあるので、預けているお金の1%を毎年ゲットできます。
さっきの計算で2年後預けているお金が102万100円であると計算できました。そのため1年間で増えるお金は101万円の1%を計算することで求められます。よって
\((\textbf{1年間で増えるお金}) = 102\text{万}100\text{円} \times 0.01 = 1\text{万}\text201{円}\)
となります。
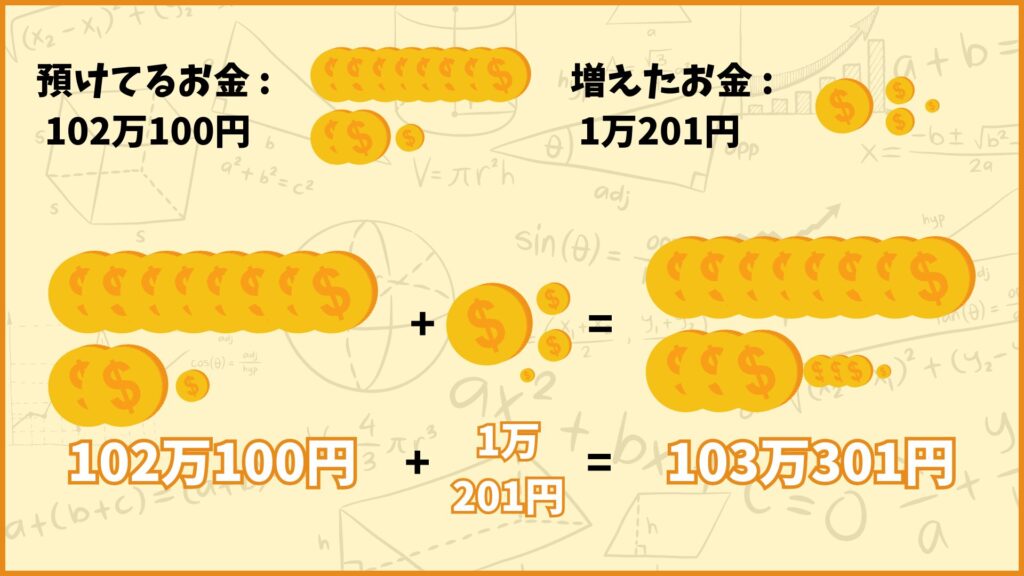
預けていた102万100円に1年間で増えた1万201円足せば3年後のたろう君のお金が求められるので
\((\textbf{3年後のお金}) = 102\text{万}100\text{円} + 1\text{万}201\text{円} = 103\text{万}301\text{円}\)
となります。つまりたろう君が預けた100万円は3年後に103万301円になっているということです。

1年間で預けているお金が1%増えるということは、預けていたお金の額が元の額の101%になると考えることもできます。このように考えると
\((\textbf{3年後のお金}) = 102\text{万}100\text{円} \times 1.01 = 103\text{万}301\text{円}\)
と計算することもできます。
ということで最初の問題は「② 103万より多い」が正解となります。
複利は増えるお金の量が毎年大きくなる
複利は利子で増えた分にも利子がつく
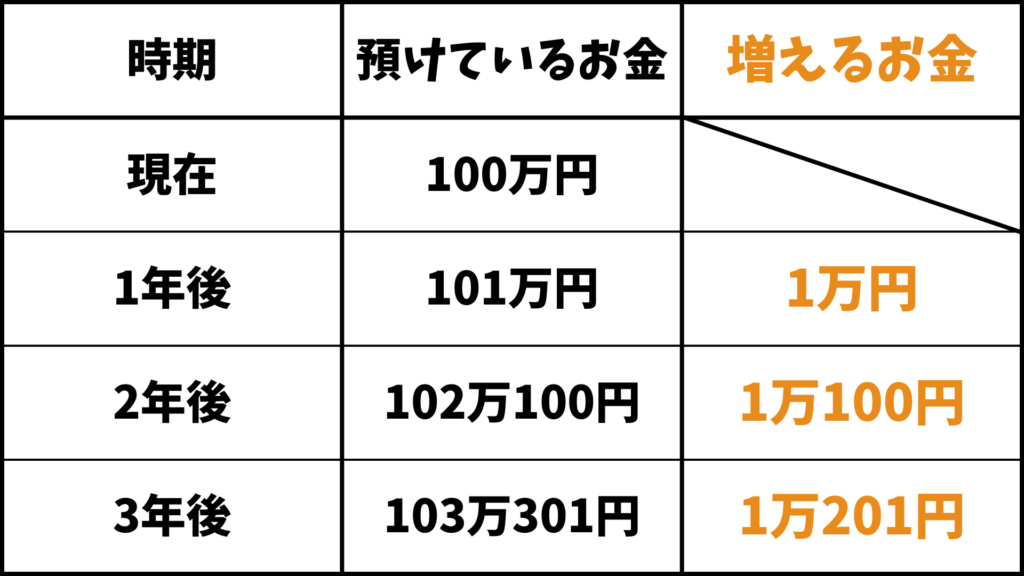
この問題の重要な所は
「複利は増えるお金の量が毎年大きくなる」
という性質です。さっきの問題を見てみると
1年後:1万円
2年後:1万100円
3年後:1万201円
と毎年増えるお金の額が大きくなっていることが分かります。なぜこうなるかと言うと、利子で増えた分のお金にも利子がつくからです。
例えば1年後~2年後の1年間で増えるお金は1万100円ですが、これは元々預けていた100万円につく利子1万円に加えて、現在~1年後の1年間で増えた1万円につく利子100円があるからです。
この「複利は増えるお金の量が毎年大きくなる」ということを理解していれば、最初の問題が②であることは計算するまでもなく答えることができます。
金利の計算方法は複利の他に単利があります。単利は利子で増えた分に利子がつかないようなときのことを言います。先ほどの具体例を使って単利の計算方法について考えてみましょう。
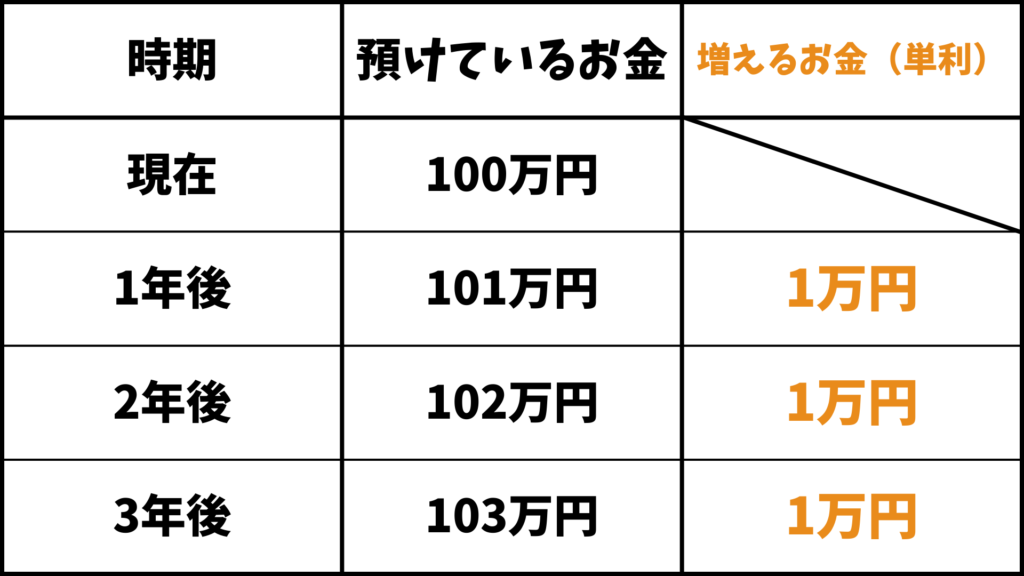
単利の場合、増えるお金は毎年100万円の1%となります。100万円の1%は1万円なので、結論単利だと毎年1万円ずつ増えていきます。そのため銀行に預けているお金は
1年後:101万円
2年後:102万円
3年後:103万円
と言う風に増えていきます。
複利と単利でどれくらい差が出るのかをグラフにしてみた
それでは複利と単利で増えるお金がどれくらい変わるのかを実際に検証してみましょう。違いを分かりやすくするために利子の年率を5%とします。最初に預けるお金は100万円として、40年間でどれくらい差が出るのかをグラフを見て確かめてみます。
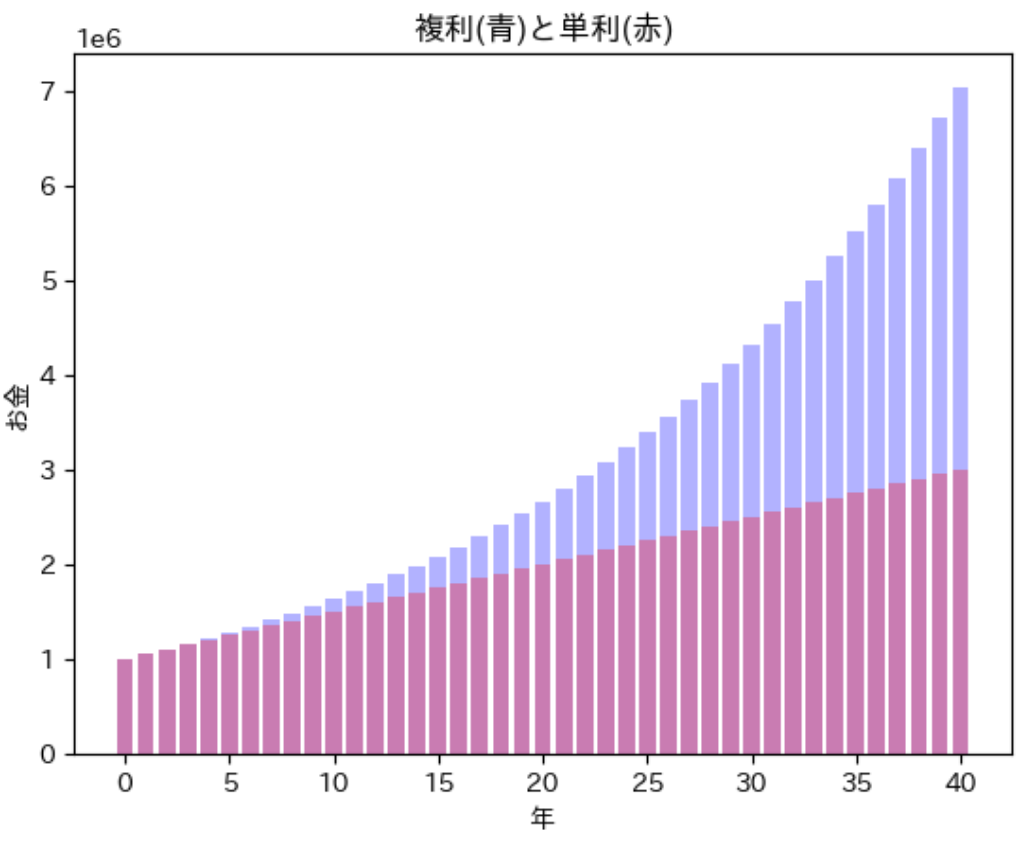
青い棒が複利、赤い棒が単利を表しています。横軸が年、縦軸がお金の額を表しています。縦軸は100万円を1目盛りとしているので、1の線は100万円、2の線は200万円になっています。
複利も単利も最初の方はあんまり変わらないですが、年月が経つにつれて差がどんどん大きくなっています。40年後を見ると2倍くらい差がついていることが分かります。
上の図はpythonというプログラミング言語を使って描画しました。以下図を描画するためのpythonのコードとなります。
import matplotlib.pyplot as plt
import japanize_matplotlib
n = 1000000
r = 0.05
x = list(range(41))
y1 = [n * (1 + r) ** i for i in x]
y2 = [n * (1 + r * i) for i in x]
plt.bar(x, y1, color = "blue", alpha = 0.3)
plt.bar(x, y2, color = "red", alpha = 0.3)
plt.xlabel("年")
plt.ylabel("お金")
plt.title("複利(青)と単利(赤)")
plt.show()数式を使って詳しく説明する
ここまでは簡単な計算の実を使って複利について説明しましたが、ここからは数式を使ってより詳しく複利について考えていきます。
記号の定義
\(a\) : 最初に銀行に預けるお金の額
\(r\) : 金利の年率
\(x\) : 年
\(y\) : \(x\)年後のお金
まず最初に数式で使う記号の定義をします。\(a\)は最初に銀行に預けるお金の額とします。最初の問題の例でいうと\(a = 1000000\)です。
\(r\)は金利の年率とします。最初の問題の例で言うと\(r = 0.01\)となります。
\(x\)は年とします。例えば20年後の話をしたければ\(x=20\)とします。
これらの記号を使って\(y\)を表してみましょう。
複利の場合
複利の数式: \(y = a(1+r)^x\)
預けたお金\(a\)円が年率\(r\)(複利)で\(x\)年後にいくらになっているかを数式で、つまり\(y\)を\(a,r,x\)を使って表すと上記のようになります。
なぜこの式で表せるのかを考えてみましょう。まず0年後、つまり現在時点では預けているお金は\(a\)円なので
(現在のお金):\(y = a\)
となります。1年後のお金(複利の場合)は、現在のお金\(a\)円に\(1+r\)を掛ければ計算できるので
(1年後のお金):\(y = a(1+r)\)
となります。2年後のお金(複利の場合)は、1年後のお金\(a(1+r)\)円に\(1+r\)を掛ければ計算できるので
(2年後のお金):\(y = a(1+r)(1+r) = a(1+r)^2\)
となります。このように考えると\(x\)年後のお金(複利の場合)は
(\(x\)年後のお金):\(y = a(1+r)^x\)
と表すことができます。
例えば\(a= 10000,r = 0.05,x = 4\)とすると、
\(y = 10000 \times (1.05)^4 = 12155.0625\)
と計算できますが、これは10000円を預けて年率5%で増えていくとき(複利)、4年後には約12155円になるということを表しています。
単利の場合
単利の数式: \(y = a(1+rx)\)
預けたお金\(a\)円が年率\(r\)(単利)で\(x\)年後にいくらになっているかを数式で、つまり\(y\)を\(a,r,x\)を使って表すと上記のようになります。
なぜこの式で表せるのかを考えてみましょう。まず0年後、つまり現在時点では預けているお金は\(a\)円なので
(現在のお金):\(y = a\)
となります。単利の場合、毎年増えるお金は\(ar\)となるので1年後のお金は
(1年後のお金):\(y = a+ar = a(1+r)\)
となります。2年後のお金は、1年後のお金\(a+ar\)円に増えた分のお金\(ar\)を足せば良いので
(2年後のお金):\(y = a+ar+ar = a+2ar=a(1+2r)\)
となります。このように考えると\(x\)年後のお金は
(\(x\)年後のお金):\(y = a(1+rx)\)
と表すことができます。
例えば\(a= 10000,r = 0.05,x = 4\)とすると、
\(y = 10000 \times (1+0.05 \times 4) = 10000 \times 1.2 = 12000\)
と計算できますが、これは10000円を預けて年率5%で増えていくとき(単利)、4年後には12000円になるということを表しています。
複利と単利の数式を比べてみる
複利の数式: \(y = a(1+r)^x\)
単利の数式: \(y = a(1+rx)\)
それでは最後に複利と単利の数式を比べてみて、どんな違いがあるかを見てみましょう。簡単のため、最初に預けるお金\(a\)と年率\(r\)は固定して、\(y\)は\(x\)の関数であるとします。
複利の数式の場合、\(y\)が\(x\)の指数関数になっている一方で、単利の数式の場合\(y\)が\(x\)の1次関数になっていることが分かります。

このように関数の種類で複利と単利の違いを考えると、複利は毎年増えるお金の額が大きくなり、単利は毎年増えるお金の額が一定であることが分かります。
おわりに
いかがでしたか。
今回の記事では複利について解説していきました。
最後までこの記事を読んでくれてありがとうございました。



