こんにちは!しゅんです!
今回の記事ではpythonを使って動的計画法でナップサック問題を解く方法を解説したいと思います!
動的計画法は最適化問題を解くための手法の1つで、ナップサック問題は組合せ最適化問題の1つです。
今回のテーマは
・手計算で動的計画法をやる
・なぜ再帰式が成り立つのか説明する
・pythonで動的計画法をやる ← 今回はここ!
の3部構成になっています!
手計算で動的計画法をやる記事はこちらです!
なぜ再帰式が成り立つの説明している記事はこちらです!
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
動的計画法でナップサック問題解くための再帰式
今回は以下の再帰式をpythonで実装したいと思います。
物が\(n\)個あり、その中の最初の\(i\)個だけから選び、重量制限が\(x\)のナップサック問題を考える。この問題の最適値を\(P(i,x)\)とすると、以下の式が成り立つ。
\(\begin{equation} P(i,x)= \begin{cases}P(i-1,x) & (a_i>x) \\ \max\{P(i-1,x),\;P(i-1,x-a_i)+c_i\} & (a_i \leq x) \end{cases} \end{equation}\)
但し\(a_i\)は物\(i\)の重量、\(c_i\)は物\(i\)の満足度
なぜこの再帰式が成り立つのかは前回の記事で解説しているので、今回はこの再帰式が成り立つと仮定してpythonを使ってナップサック問題を動的計画法で解く方法を説明したいと思います。
なぜ再帰式が成り立つのかを説明している記事はこちらから!
pythonで実装する
結論以下のコードを実行することでナップサック問題を動的計画法で解くことができます。
## ナップサック問題を解く関数
def knapsack(cost, value, x, memo=None):
if memo is None: # メモを初期化する
memo = {}
if (len(cost), x) in memo: # メモがある場合はそれを返す
return memo[(len(cost), x)]
if len(cost) == 0 or x < 1: # P(0,x), P(i,0)のとき
return 0, [] # 0と空リストを返す(空リストは最適解を返すときに使う)
elif cost[-1] > x: # 物iの重みがxより大きいとき
result = knapsack(cost[:-1], value[:-1], x, memo) # 物iは選ばないのでP(i-1,x)をresultに格納
memo[(len(cost), x)] = result # メモ化
return memo[(len(cost),x)] # メモを返す
else: # 物iの重みがx以下のとき
ai = cost[-1] # 物iの重みにaiと名付ける
ci = value[-1] # 物iの満足度にciと名付ける
without_i, without_i_items = knapsack(cost[:-1], value[:-1], x, memo) # 物iを選ばないとき:P(i-1,x)
with_i, with_i_items = knapsack(cost[:-1], value[:-1], x - ai, memo) # 物iを選ぶとき:P(i-1,x-ai)
with_i += ci # 最適値にciを足す
if with_i > without_i: # iを選ぶときの方がiを選ばないときより満足度が大きい場合
result = with_i, with_i_items + [len(cost) - 1] # P(i-1,x-ai)+ciをresultに格納(with_i_itemsに物iのインデックスを追加)
else: # iを選ばないときの方がiを選ぶときより満足度が大きい場合
result = without_i, without_i_items # P(i-1,x)をresultに格納
memo[(len(cost), x)] = result # メモ化
return memo[len(cost),x]今回は関数として定義しました。引数は各物の重さを表すリストのcost、各物の満足度を表すリストのvalue、重量制限をあらわすx、メモ用の辞書memoの4のつです。memoは何も入力しなかったらNoneになるようにしています。
返す値は最適値と最適解のリストの2種類です。それでは1つずつ解説していきます。
関数の定義
## ナップサック問題を解く関数
def knapsack(cost, value, x, memo=None):1~2行目で関数の定義をしています。分かりやすいようにknapsackと名前を付けています。再帰式の方では\(P(i,x)\)と名前を付けていました。
メモの初期化
if memo is None: # メモを初期化する
memo = {}3~4行目でメモの初期化を行っています。もしmemoがNoneだったら空辞書をメモとして使います。memo={}をデフォルト引数にして問題を2個解くと、2個目の問題で使われるmemoが1個目のmemoを引き継いでしまいました。
そのためまず最初にmemoを初期化する作業を入れて、何回問題を解いてもメモが空辞書からスタートするように設定しています。
メモに値が入っているか確認
if (len(cost), x) in memo: # メモがある場合はそれを返す
return memo[(len(cost), x)]6~7行目でメモに値が入っているかを確認しています。\(P(i,x)\)の値のメモがある場合は、もう一度計算する必要が無いのでそれをそのまま返します。イメージ的には、このメモは計算編の記事で使った表のことです。
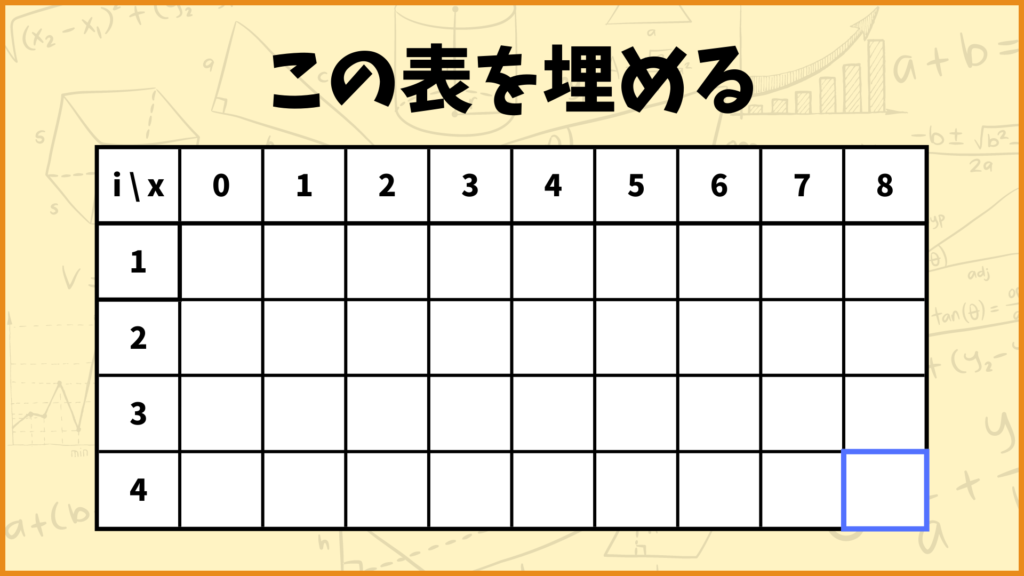
動的計画法ではこのメモをどんどん埋めていく作業をやります。一度計算した値を使い回したいので、メモに書いて保存しきます。このようにすることで無駄な計算を省き計算時間を短くすることができるというわけです。
動的計画法の計算時間についてはこちらの記事で説明しています!
現在制作中
\(P(0,x),\;P(i,0)\)の定義
if len(cost) == 0 or x < 1: # P(0,x), P(i,0)のとき
return 0, [] # 0と空リストを返す(空リストは最適解を返すときに使う)9~10行目で\(P(0,x),\;P(i,0)\)の定義をしています。\(i=0\)のときはcostの要素数が0なので、len(cost)==0で検知して、\(x=0\)はそのままx<1で検知しています。
\(i=0\)のときも\(x=0\)のときも最適値は0、最適解は何も選ばない(というか選べない)ので0と空リストを返しています。
\(a_i > x\)の場合
elif cost[-1] > x: # 物iの重みがxより大きいとき
result = knapsack(cost[:-1], value[:-1], x, memo) # 物iは選ばないのでP(i-1,x)をresultに格納
memo[(len(cost), x)] = result # メモ化
return memo[(len(cost),x)] # メモを返す12~15行目で\(a_i>x\)、すなわち物\(i\)の重さが重量制限\(x\)よりも大きい場合を設定しています。物\(i\)の重さはcostリストの一番最後に格納されているので、cost[-1]でその値を取りだしてxと比較しています。
\(a_i>x\)はcost[-1] > xで表現できます。このときは\(P(i,x)=P(i-1,x)\)となるので\(P(i-1,x)\)をpythonで表現してresultに格納し、それをメモに加えています。
\(P(i-1,x)\)はknapsack(cost[:-1], value[:-1], x, memo)で表せます。cost[:-1]はcostリストの一番最後の値、すなわち\(a_i\)だけを取り除いたリストになります。value[:-1]も同じです。この2つで\(i-1\)を表現しています。
memoはこの関数内で何度も更新されますが、常に最新のものを使いたいので引数に入れておきます。もし引数にmemoを入れておかなければデフォルト引数が設定されてしまうので13行目で再帰するときは引数にmemoを入れておきます。
14行目でresultの値をメモして、15行目でメモした値を返しています。
\(a_i \leq x\)の場合
17~30行目で\(a_i \leq x\)、すなわち物\(i\)の重さが重量制限\(x\)以下の場合を設定しています。この部分は結構長いのでさらに5つに分解して説明していきます。
18~19行目
ai = cost[-1] # 物iの重みにaiと名付ける
ci = value[-1] # 物iの満足度にciと名付ける分かりやすくするために物\(i\)の重さにai、満足度にciと名前を付けています。
20行目
without_i, without_i_items = knapsack(cost[:-1], value[:-1], x, memo) # 物iを選ばないとき:P(i-1,x)物\(i\)を選ばない場合を設定しています。knapsack関数は最適値と最適解を返す関数なので、最適値にwithout_i、最適解にwithout_i_itemをそれぞれ割り当てています。
cost[:-1]、value[:-1]でそれぞれのリストの最後の要素以外を取り出しています。xは特に変える必要が無いのでそのままxにします。数式で言うと\(P(i-1,x)\)を設定しています。
21~22行目
with_i, with_i_items = knapsack(cost[:-1], value[:-1], x - ai, memo) # 物iを選ぶとき:P(i-1,x-ai)
with_i += ci # 最適値にciを足す物\(i\)を選ぶ場合を設定しています。with_iに最適値、with_i_itemに最適解を割り当てています。cost, valueはさっきと同じですが、物\(i\)を選ぶときは\(x \to x-a_i\)になるのでx-aiにします。
このままだとwith_iの値が\(P(i-1,x-a_i)\)だけになってしまうので、14行目で\(c_i\)を加えています。数式で言うと\(P(i-1,x-a_i)+c_i\)を設定しています。
24~29行目
if with_i > without_i: # iを選ぶときの方がiを選ばないときより満足度が大きい場合
result = with_i, with_i_items + [len(cost) - 1] # P(i-1,x-ai)+ciをresultに格納(with_i_itemsに物iのインデックスを追加)
else: # iを選ばないときの方がiを選ぶときより満足度が大きい場合
result = without_i, without_i_items # P(i-1,x)をresultに格納
memo[(len(cost), x)] = result # メモ化without_iとwith_iのうち大きい方を返すように設定しています。最初はmax関数を使おうと思ったのですが、with_iとwithout_iを比べて大きい方を返すときに最適解も一緒に返す方法が分からなかったので条件分岐で表現しました。
with_i > without_iのときは物\(i\)を選ぶ方が満足度の合計が大きいのでwith_iとwith_i_items+[len(cost)-1]をresultに格納します。
[len(cost)-1]を追加したのは物iのインデックスを追加するためです。最初は22行目の後にwith_i_items+=[len(cost)-1]を付けましたが、それだと再帰呼び出しを繰り返す際に不具合が生じ、うまくいきませんでした。
without_i > with_iのときは物\(i\)を選ばない方が満足度の合計が大きいのでwithout_iとwithout_i_itemsをresultに格納します。
最後にmemoにresultを加えています。
30行目
return memo[len(cost),x]
最後に\(P(i,x)\)を返しています。
実際に問題を解いてみる
それでは今作った関数を使って実際に問題を解いてみましょう。まず最初に計算編で紹介したナップサック問題の例を、pythonで解いてみます。
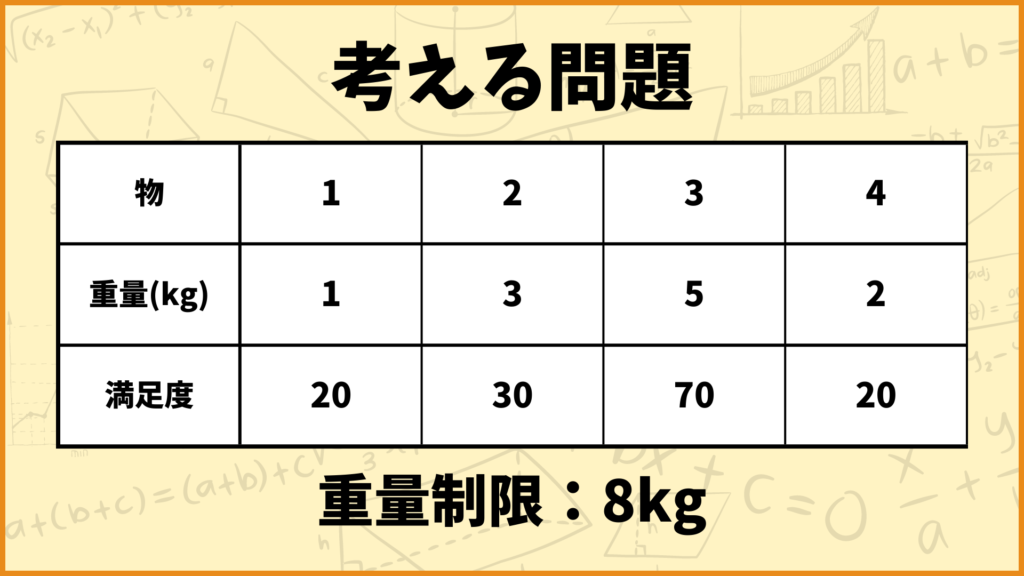
C = [1,3,5,2] # 重さを設定
V = [20,30,70,20] # 満足度を設定
X = 8 # 重量制限を設定
knapsack(C,V,X) # ナップサック問題を解く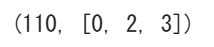
ということで最適値と最適解を求めることができました。最適値が110、最適解が[0,2,3]です。pythonはインデックスが0から始まるので実際には物1、物3、物4を選ぶのが最も良いということです。
まあこの程度の問題なら自分で計算しても求まっちゃいますね。ということでもっとデータ数を大きくしてみましょう。今度は20個の物の中から最適な組合せを見つけます。
物1から物20の重さと満足度をランダムに設定してナップサック問題を解いていきます。まず最初に重さと満足度と重量制限を設定します。
import random
random.seed(1) # ランダム値を固定する
C = [random.randint(1,8) for i in range(20)] # ランダムに重さを20個生成
V = [random.randint(10,90) for i in range(20)] # ランダムに満足度を20個生成
X = 20 # 重量制限を設定
本題じゃないので詳しくは説明しませんが、上のコードは重さと満足度をそれぞれランダムに20個設定、そして重量制限を設定しています。
重さは1kg~8kgの範囲の整数をランダムに設定してCという名前を付けています。満足度は10~90の範囲の整数をランダムに設定してVという名前を付けています。重量制限は20設定してXという名前を付けています。
重さと満足度にどのような値が割り振られているかを確認してみましょう。
import pandas as pd
df = pd.DataFrame([C,V],index = ["重さ","満足度"], columns = [f"物{i}" for i in range(1,21)])
df
こんな感じの分布になっています。それではこのデータ値に対してknapsack関数を適用してみましょう。
knapsack(C,V,X)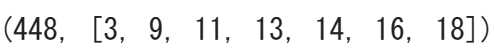
ということで最適値が448、最適解が物4、物10、物12、物14、物15、物17、物19であることが分かりました。満足度を重さで割った値で並べ替えてみた結果が下の表です。

これを見ると最適解のうち物17以外の6つが満足度/重さのTOP6になっています。やはり効率よく満足度を得られる物を選ぶ傾向があるということですね。
動的計画法を使うのと使わないのとでは計算時間がかなり違います。下の記事では実際にどれくらい計算時間が違うのかを検証しているのでこちらもぜひ見てみてください!
現在制作中
おわりに
いかがでしたか。
今回の記事ではpythonを使ってナップサック問題を解く方法について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。