こんにちは!しゅんです!
今回の記事では動的計画法でナップサック問題を解くときに登場する再帰式の解説をしたいと思います!
動的計画法は最適化問題を解くための手法の1つで、ナップサック問題は組合せ最適化問題の1つです。
今回のテーマは
・手計算で動的計画法をやる
・なぜ再帰式が成り立つのか説明する ← 今回はここ!
・pythonで動的計画法をやる
の3部構成になっています!
手計算で動的計画法をやる記事はこちらです!
pythonで動的計画法を実装する方法は記事はこちらです!
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
動的計画法でナップサック問題解くための再帰式
今回は以下の再帰式を用いることでナップサック問題が解けます。
物が\(n\)個あり、その中の最初の\(i\)個だけから選び、重量制限が\(x\)のナップサック問題を考える。この問題の最適値を\(P(i,x)\)とすると、以下の式が成り立つ。
\(\begin{equation} P(i,x)= \begin{cases}P(i-1,x) & (a_i>x) \\ \max\{P(i-1,x),\;P(i-1,x-a_i)+c_i\} & (a_i \leq x) \end{cases} \end{equation}\)
但し\(a_i\)は物\(i\)の重量、\(c_i\)は物\(i\)の満足度
例えば最初の3個から物を選び、重量制限が5kgのサブ問題の最適値は\(P(3,5)\)となります。元の問題の重量制限を\(b\)kgとすると、元の問題の最適値は\(P(n,b)\)となります。
この記事ではなぜ上の再帰式が成り立つのかを考えてみたいと思います。
再帰式が言っていることを言葉で理解する
まずはこの再帰式が何を言っているのかを理解する必要があります。1つずつ見てみましょう。
\(P(i,x)\)は物1から物\(i\)までの中から重量制限が\(x\)kgのナップサックに何を入れるかを考える問題の最適値です。

\(P(3,x)\)は物1~物3の中から選び、\(P(5,x)\)は物1から物5の中から選ぶことに注意してください。そう考えると、直観的に\(P(1,x)\)が一番簡単に最適値を求めることができそうです。

次に\(a_i>x\)の場合について考えます。これは物\(i\)の重量が、重量制限\(x\)を超えている場合ということです。つまりこの時点で物\(i\)を持っていくことはできないということです。
このときは\(P(i,x)=P(i-1,x)\)、すなわち物1から物\(i-1\)の中から重量制限\(x\)の範囲で選ぶときの最適値と同じだと言っています。
最後に\(a_i \leq x\)の場合について考えます。これは物\(i\)の重量が、重量制限\(x\)を超えていない場合ということです。つまり物\(i\)を選ぶ可能性があるということです。
このときは\(P(i-1,x)\)と\(P(i-1,x-a_i)+c_i\)のうち大きい方を採用します。
動的計画法のポイント
再帰式が成立することを理解するためには、動的計画法のポイントを知っておくとこの先の説明が理解しやすいと思います。
動的計画法のポイントは
既に計算した値を使って問題を解いていく
です。動的計画法でナップサック問題を解くときは下のような表を使うと理解しやすいです。
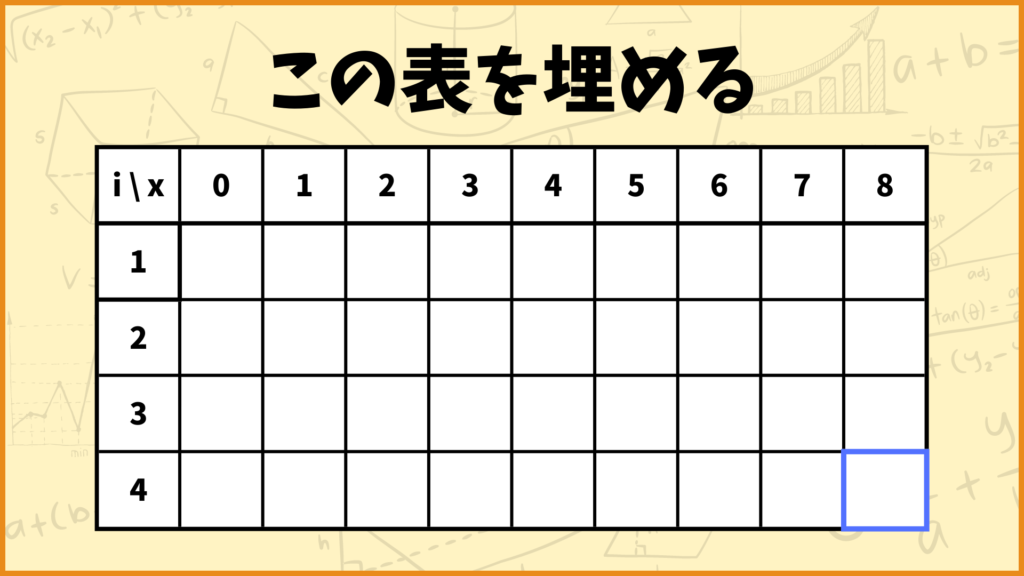
この表の左の1,2,3,4が物1~物4を表していて、上の1,2,,…,8が重量制限を表しています。例えば\(i=2,\;x=5\)のマスは物1、物2の中から重量制限5kgの中での最適値が入ります。
いきなり\(P(4,8)\)を求めるのは難しいので、\(P(1,0)\)から順番に最適値を求めるのが動的計画法の考え方です。

つまり例えば\(P(3,5)\)を求めたいときは、上図の青い範囲の中の数値を使って表せないかと考えます。このことに注意してみると、なぜあの再帰式は\(P(i,x)\)を\(P(i-1,x),\;P(i-1,x-a_i)\)を使って表しているのかが分かるかと思います。
なぜあの再帰式が成り立つのかを説明する
それではいよいよなぜあの再帰式が成り立つのかを説明したいと思います。あの再帰式を再掲しておきます。
物が\(n\)個あり、その中の最初の\(i\)個だけから選び、重量制限が\(x\)のナップサック問題を考える。この問題の最適値を\(P(i,x)\)とすると、以下の式が成り立つ。
\(\begin{equation} P(i,x)= \begin{cases}P(i-1,x) & (a_i>x) \\ \max\{P(i-1,x),\;P(i-1,x-a_i)+c_i\} & (a_i \leq x) \end{cases} \end{equation}\)
但し\(a_i\)は物\(i\)の重量、\(c_i\)は物\(i\)の満足度
\(Case.1\; : \; a_i>x\)のとき
\(a_i>x\)のときは結構簡単に考えることができます。これは物\(i\)の重さが重量制限\(x\)を超えているということです。つまり物\(i\)を選ぶことができません。
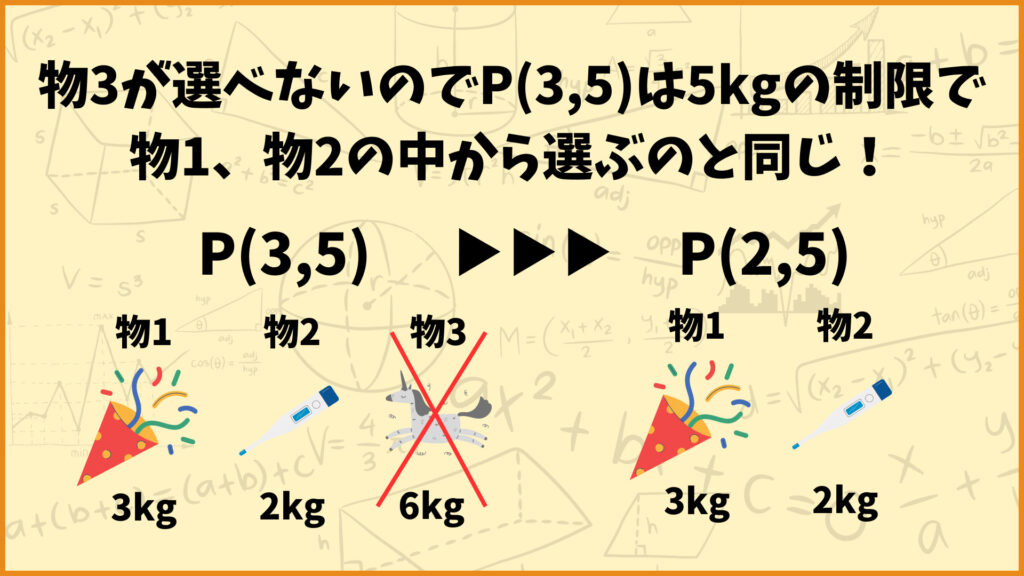
\(P(3,5)\)について考えます。仮に\(a_3=6\)だとすると、物3を選ぶことができません。この状態って重量制限5kgで物1、物2の中から選ぶのと同じですよね。つまり\(P(3,5)=P(2,5)\)となります。
これを一般化すると、物\(i\)の重み\(a_i\)が重量制限\(x\)を超えているときは\(P(i,x)=P(i-1,x)\)が成立しますね。
\(P(i,x)=P(i-1,x)\;\;\;\;\;\;(a_i>x)\)
\(Case.2\; : \; a_i \leq x\)のとき
\(a_i \leq x\)のときは少し複雑です。このとき物\(i\)の重さ\(a_i\)は重量制限\(x\)以下となるので、物\(i\)を選ぶことができます。ここでさらに2つのパターンに分かれます。

1つは物\(i\)を選ぶパターンで、もう1つは物\(i\)を選ばないパターンです。両方のパターンを考えて、より満足度の合計が多い方を採用しましょう。
すなわち\(P(i,x)\)を下のような感じで表したいということです。
\(P(i,x)=\max\{ \text{物} i \text{を選ばないときの満足度の合計} , \; \text{物} i \text{を選ぶときの満足度の合計} \}\)
ということでここからは物\(i\)を選ばないときの満足度の合計と、物\(i\)を選ぶときの満足度の合計がそれぞれどのように表されるかを考えていきましょう。
パターン1:物\(i\)を選ばない場合
まず物\(i\)を選ばないときについて考えましょう。とは言ってもこのパターンは\(Case.1\)と同じです。物\(i\)を選ばないので、重量制限\(x\)で物1から物\(i-1\)の中から選ぶのと同じになります。
従ってこのパターンの場合は
\(P(i,x)=P(i-1,x)\) (物\(i\)を選ばない)
という風に表せます。
パターン2:物\(i\)を選ぶ場合
次に物\(i\)を選ぶ場合について考えましょう。

簡単のため、重量制限が\(x=8\)kgで物\(i\)の重さが\(a_i=3\)kgだとします。物\(i\)を選ぶので8kg中3kgは物\(i\)のために使います。そうすると残りは8kg-3kg=5kgとなるので、残り5kgで物1~物\(i-1\)の中から選ばないといけません。

重量制限5kgで物1~物\(i-1\)の中から選ぶとき、その最適値は\(P(i-1,5)\)と表されます。そしてそこに物\(i\)の満足度\(c_i\)を加えれば\(P(i,8)\)の値になりますね。
このことを一般化しましょう。物\(i\)の重さを\(a_i\)としましょう。重量制限\(x\)で物\(i\)を選ぶとき、重量制限\(x-a_i\)で残りの物1~物\(i-1\)の中から選ぶ必要があります。
このときの最適値は\(P(i-1,x-a_i)\)となります。ここに物\(i\)の満足度\(c_i\)を加えることで元の問題の最適値\(P(i,x)\)を求めることができます。
\(P(i,x)=P(i-1,x-a_i)+c_i\) (物\(i\)を選ぶ)
2つのパターンのうち大きい方を採用する
そして最後にこの2つのパターンのうち、満足度の合計がより大きい方を採用するので、最終的に\(a_i \leq x\)の場合、\(P(i,x)\)は以下のように表すことができます。
\(P(i,x)=\max\{P(i-1,x), \; P(i-1,x-a_i)+c_i\}\;\;\;(a_i \leq x)\)
ということで\(Case.1,\; Case.2\)の2つの場合について\(P(i,x)\)を表す式を作ることができました。
最後にこの2つをまとめると今回ずっと話していた再帰式を得ることができます。
物が\(n\)個あり、その中の最初の\(i\)個だけから選び、重量制限が\(x\)のナップサック問題を考える。この問題の最適値を\(P(i,x)\)とすると、以下の式が成り立つ。
\(\begin{equation} P(i,x)= \begin{cases}P(i-1,x) & (a_i>x) \\ \max\{P(i-1,x),\;P(i-1,x-a_i)+c_i\} & (a_i \leq x) \end{cases} \end{equation}\)
但し\(a_i\)は物\(i\)の重量、\(c_i\)は物\(i\)の満足度
おわりに
いかがでしたか。
今回の記事では動的計画法の再帰式について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。