- オイラー(閉)路、ハミルトン(閉)路ってなに?
- オイラー閉路、ハミルトン閉路が存在する条件は?
- 一筆書きとオイラー路って同じなの?
こんにちは!しゅんです!
今回はオイラー路とハミルトン路について解説していきます!
オイラー路とハミルトン路はどちらもグラフ理論で登場する数学用語です。
ということでこの記事ではオイラー路とハミルトン路とは何なのかを説明していきたいと思います。この記事の最後にはオイラー路と一筆書きの関係についても解説するのでぜひ見てみてください!
それでは解説していきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
オイラー路ってなに?
オイラー路はグラフ中にあるすべての辺を丁度1回通るような路のことを言います。下の図を見てください。
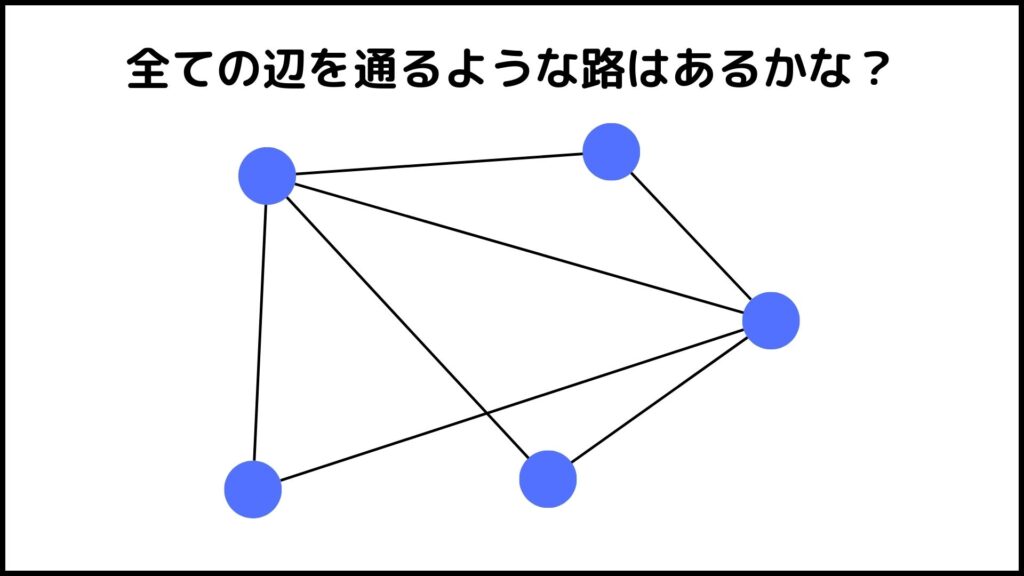
この図を見ると5個の頂点と7本の辺でグラフが構成されています。このグラフの7本の辺をすべて通るようなオイラー路はあるでしょうか。
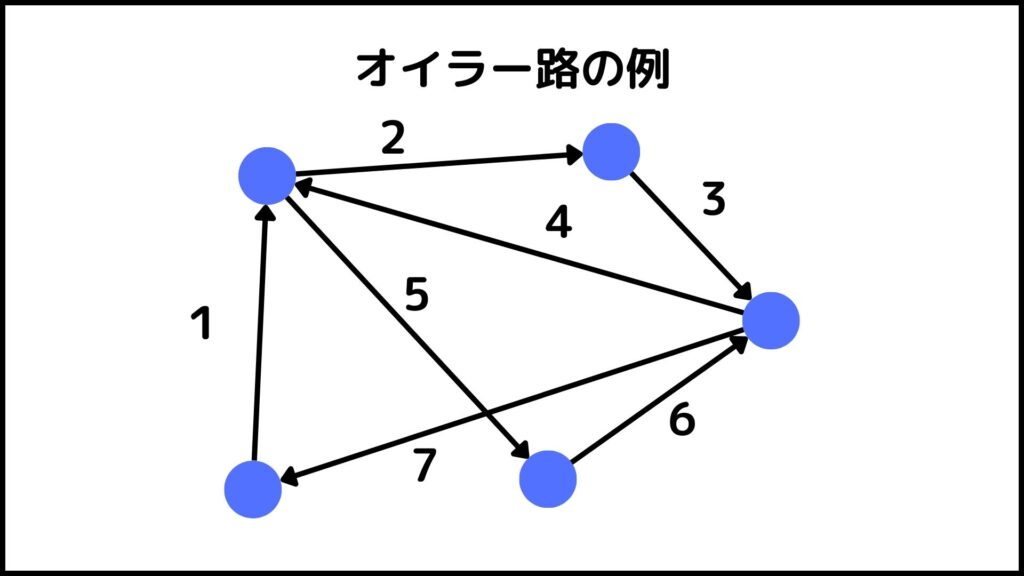
上図はオイラー路の一例です。この順番で矢印の通りに進んでいけばすべての辺を丁度一度通るようなオイラー路ができますね。
始点と終点が同じ頂点の場合はオイラー閉路という
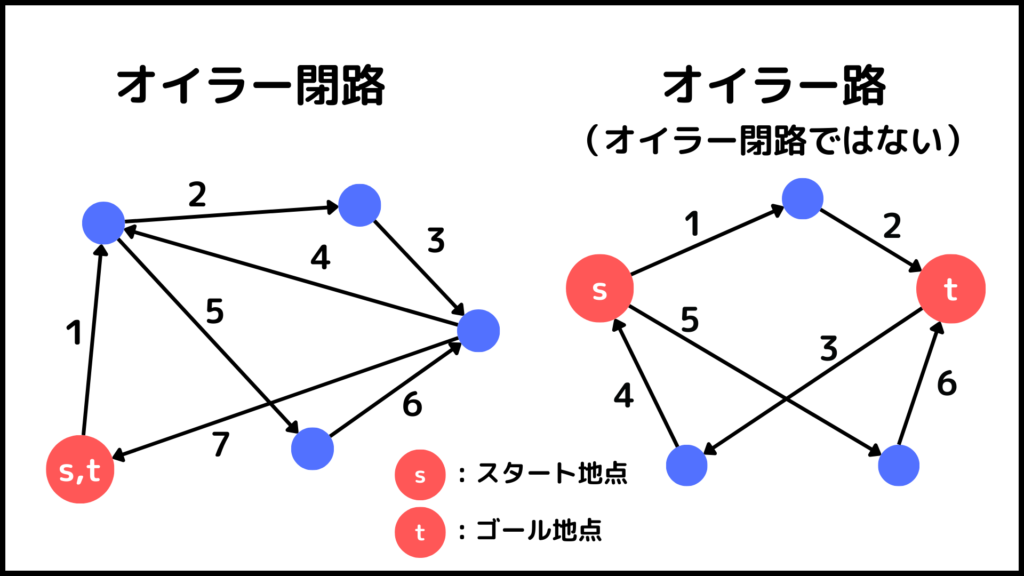
左上のグラフを見ると左下の頂点からスタートしてオイラー路を通って最終的にスタートと同じ左下の頂点にゴールしていますね。
このようにスタートの点(始点)とゴールの点(終点)が同じオイラー路を特別に
「オイラー閉路」と呼びます。
オイラー路(閉路)ができる条件
オイラー(閉)路ができる条件を説明する前に次数という用語について説明したいと思います。次数とは頂点と接続している辺の本数のことです。例えば下の図を見てください。
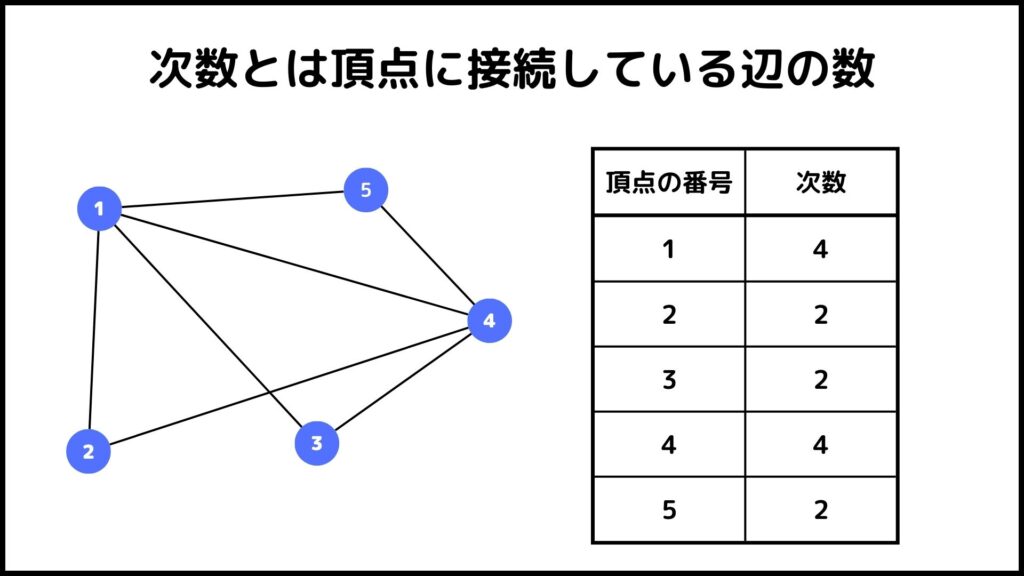
上図は左のグラフの各頂点の次数をまとめたものです。例えば頂点1には4本の辺がくっついていますね。すなわち次数は4になります。他にも頂点2を見ると2本の辺がくっついているため次数は2になります。
次数はよく\(\text{deg}\)で表し、例えば頂点\(v\)の次数が3のときは\(\text{deg}(v) = 3\)と表します。
オイラー路ができる条件
オイラー路ができる条件は以下の通りです。
次数が奇数の頂点を0個または2個持つ
例えば下のグラフは奇数の頂点が2個なのでこのようなオイラー路が存在します。
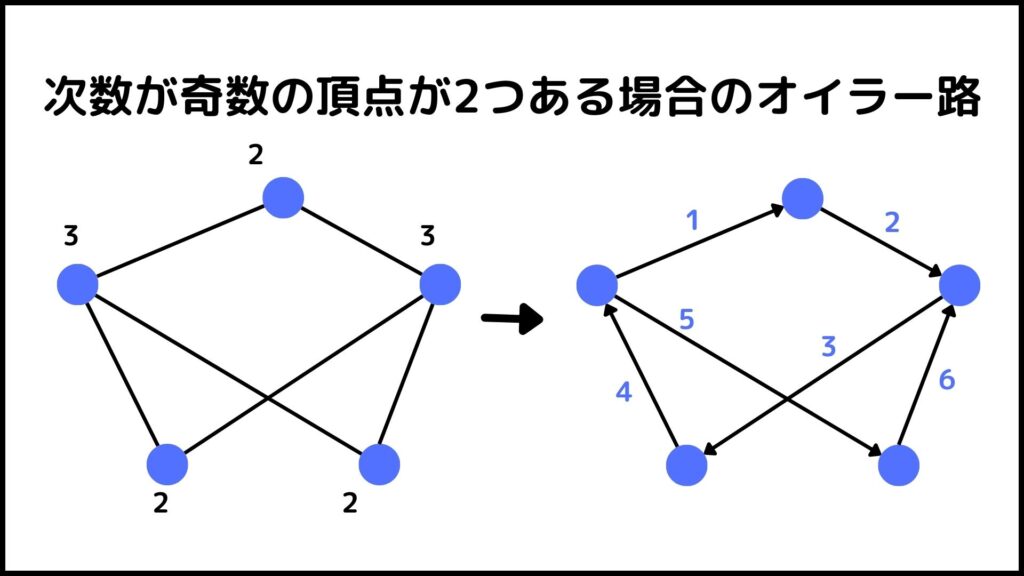
下のグラフは次数が奇数の頂点が4つなのでオイラー路は存在しません。

またオイラー閉路ができる条件は以下の通りです。
全ての頂点の次数が偶数である
下のグラフはオイラー閉路を持ちます。
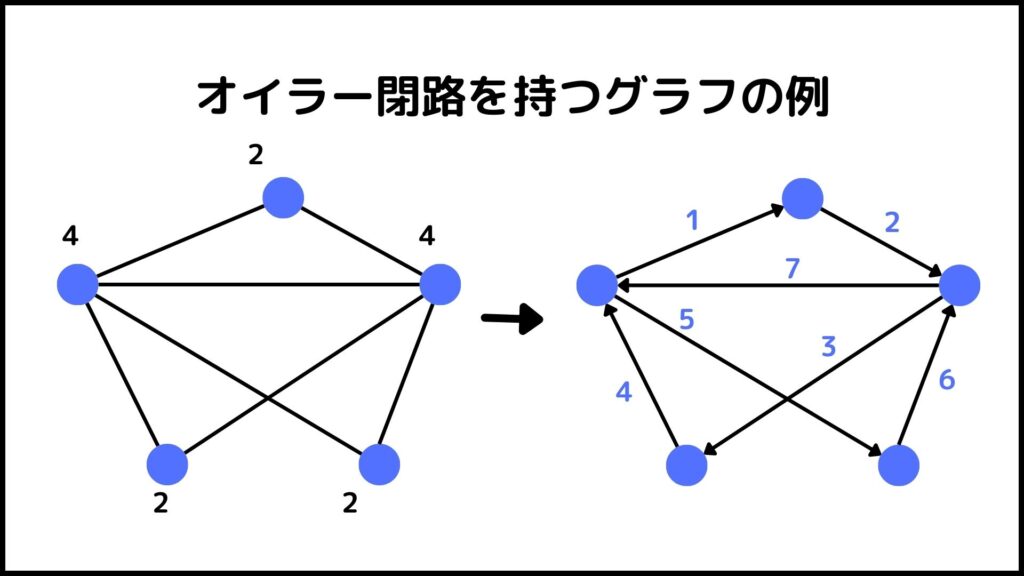
ちゃんと説明するとグラフがオイラー路、オイラー閉路を持つための必要十分条件は
オイラー路:次数が奇数の頂点が0個または2個持つ
オイラー閉路:全ての頂点の次数が偶数である
となります。
ハミルトン路ってなに?
ハミルトン路はグラフ中にあるすべての頂点を丁度1回通るような路のことを言います。下の図を見てください。

この図を見ると5個の頂点と7本の辺でグラフが構成されています。このグラフの7本の辺をすべて通るようなハミルトン路はあるでしょうか。
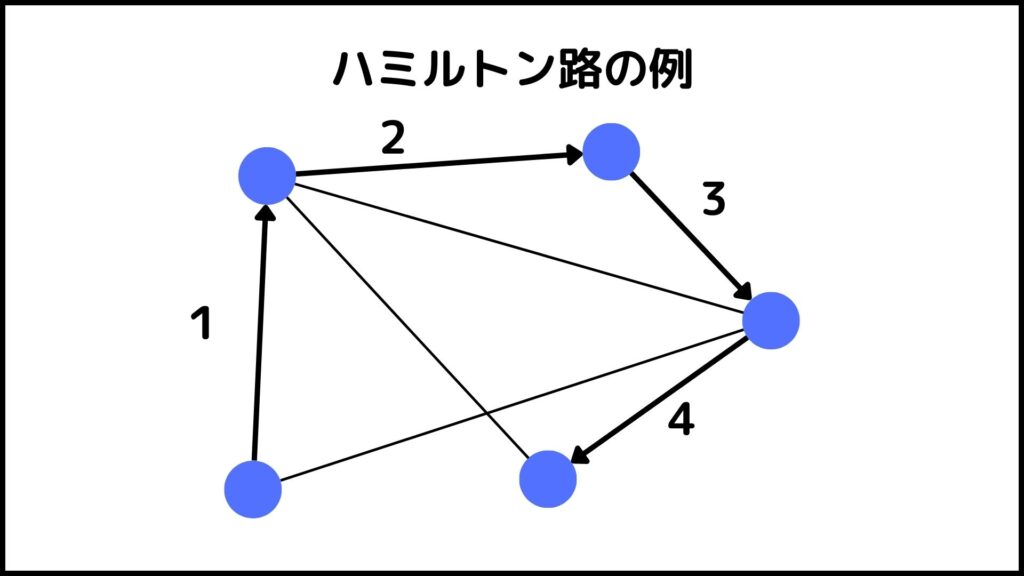
上図はハミルトン路の一例です。この順番で矢印の通りに進んでいけばすべての頂点を丁度一度通るようなハミルトン路ができますね。
ハミルトン路の場合はすべての頂点さえ通れば大丈夫なので通らない辺があっても問題ないです。
始点と終点が同じ頂点の場合はハミルトン閉路という
ハミルトン路の中でも特に始点と終点が同じ場合はハミルトン閉路と言います。例えば下のグラフにおいて矢印で表した閉路はハミルトン閉路となります。
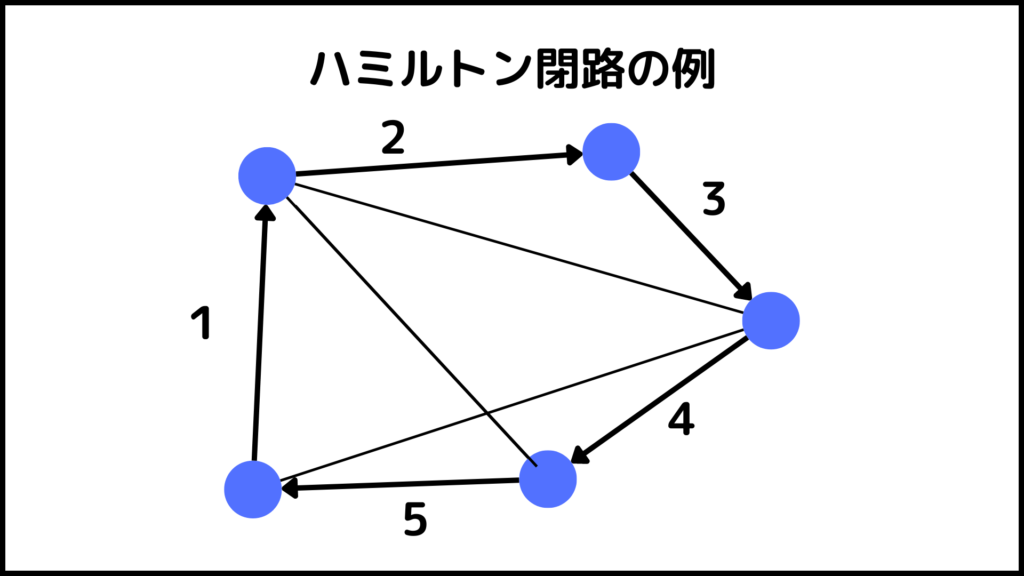
厳密に言うとハミルトン閉路の始点(終点)は2回通っています。
ハミルトン閉路ができる条件
オイラー路(閉路)のときとは違ってハミルトン路(閉路)ができるためのちゃんとした条件はありません。(数学用で言うと必要十分条件のこと)
その代わりに、これを満たしてれば少なくともハミルトン閉路を持つっていう条件(十分条件)はいくつかあります。
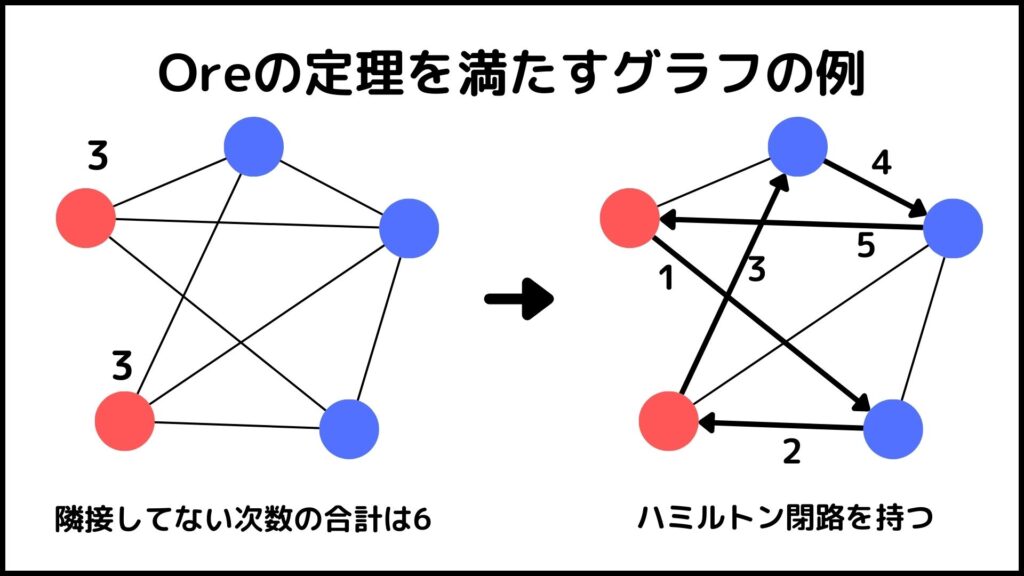
Oreの定理
単純グラフの頂点数\(n\)が3以上のときに、隣接していない(直接辺で繋がっていない)任意の2つの頂点\(v\)と\(w\)に対して、
\(\text{deg}(v)+\text{deg}(w) \geq n\)
が成立するならば、そのグラフはハミルトン閉路を持つ。
※単純グラフとは、自己ループや多重辺を持たないグラフのこと。
例えば下のグラフはOreの定理を満たすのでハミルトン閉路を持ちます。
Diracの定理
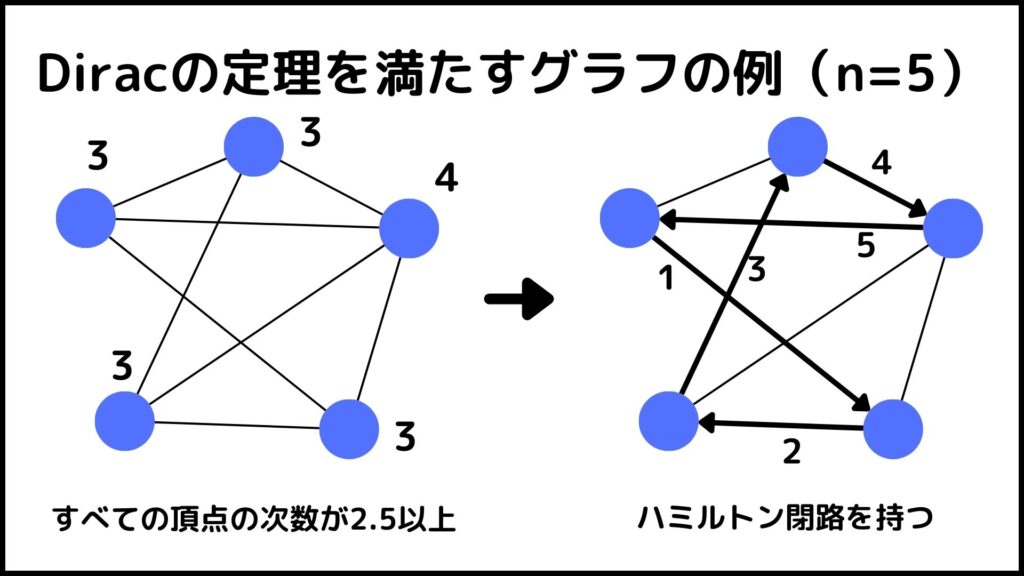
単純グラフの頂点数\(n\)が3以上のとき、グラフ中のすべての頂点\(v\)の次数が
\(deg(v)\geq \frac{1}{2} n\)
を満たすときそのグラフはハミルトン閉路を持つ。
※単純グラフとは、自己ループや多重辺を持たないグラフのこと。
例えば下のグラフはDiracの定理に当てはまっているのでハミルトン閉路を持ちます。
ということでハミルトン閉路を持つための条件であるOreの定理とDiracの定理を紹介しましたが、どちらも結局辺がたくさんあればハミルトン閉路を持つよってことを言っています。
一筆書きはオイラー路のこと
最後にこれまで話してきたことと一筆書きの関連性について話したいと思います。結論一筆書きはオイラー路のことです。
オイラー路について復習すると、全ての辺を通るような路がオイラー路でした。これってつまり一筆書きですよね。

つまり一筆書きができるかどうか判断するときは全ての頂点の次数を見て、奇数次数の頂点数が0か2だったら一筆書きで行けるということですね。
おわりに
いかがでしたか。
今回の記事ではオイラー路とハミルトン路について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。




