排他的論理和\(\oplus\)は論理変数\(x,\;y\)に対して
\(x \oplus y = x\bar{y} \vee \bar{x}y\)
となる。
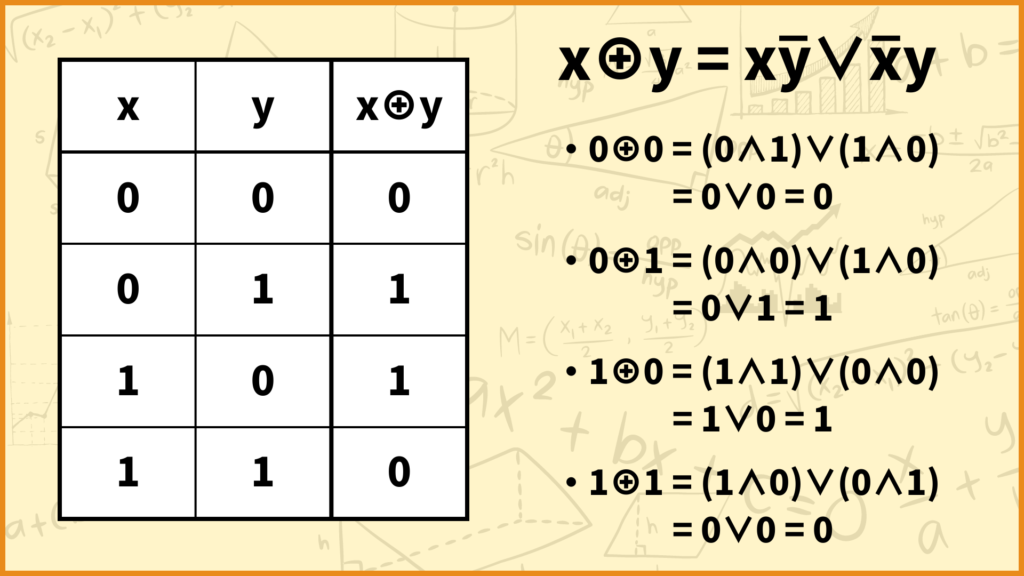
排他的論理和を簡単に説明すると\(x\)と\(y\)の値が一緒のときは0を取り、異なるときは1を取ります。
排他的論理和（EXOR）の性質
排他的論理和\(\oplus\)は以下の式が成り立ちます。
1つ目：\(x \oplus y = y \oplus x\)
2つ目：\((x \oplus y) \oplus z = x \oplus (y \oplus z)\)
3つ目：\(x \wedge (y \oplus z) = (x \wedge y) \oplus (x \wedge z)\)
4つ目：\(x \oplus 0 = x\)
5つ目：\(x \oplus 1 = \bar{x}\)
6つ目：\(x \oplus x = 0\)
7つ目：\(x \oplus \bar{x} = 1\)
それぞれ成立するのを確認してみましょう。
排他的論理和（EXOR）の性質を確かめる
1つ目
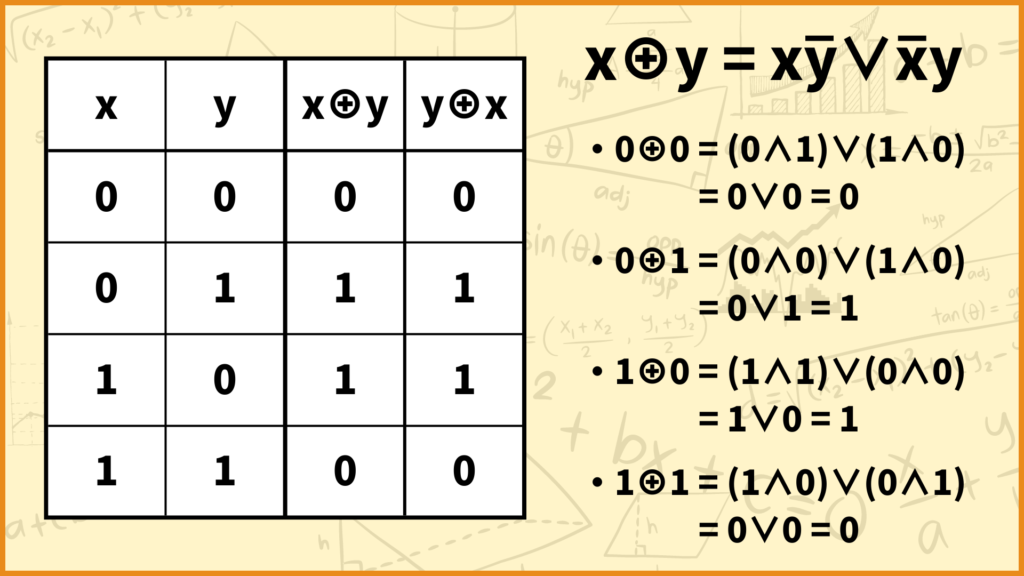
1つ目：\(x \oplus y = y \oplus x\)
これはすぐにわかりますね。\(x \oplus y = x\bar{y} \vee \bar{x}y = \bar{x}y \vee x\bar{y} = y \oplus x\)なことからも分かります。
この性質は交換律と呼ばれます。
2つ目
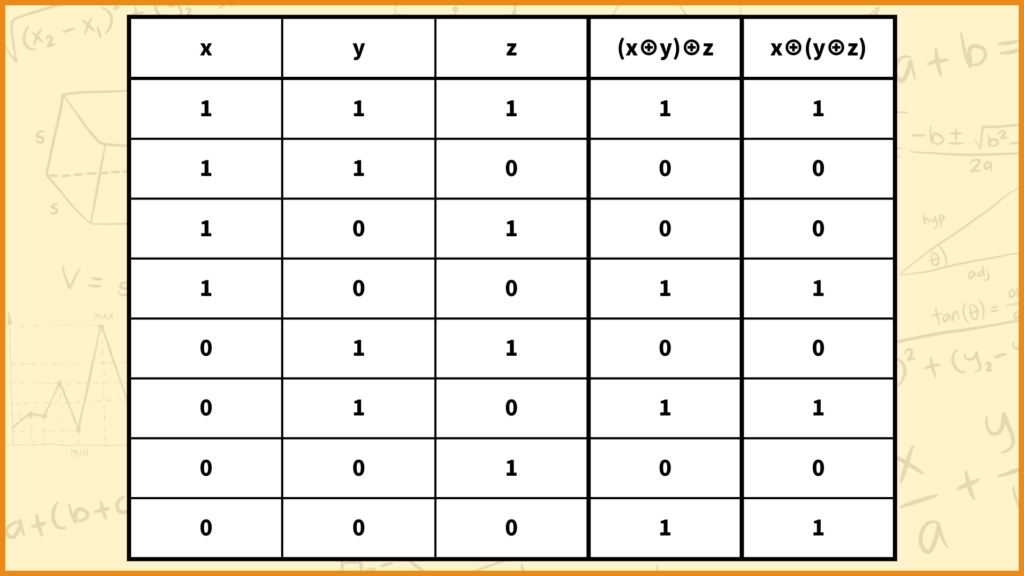
2つ目：\((x \oplus y) \oplus z = x \oplus (y \oplus z)\)
上の表の右側の列2つを計算すると\((x \oplus y) \oplus z = x \oplus (y \oplus z)\)が成り立つのが分かります。
この性質は結合律と呼ばれます。
\((1 \oplus 1) \oplus 1 =0 \oplus 1 = 1\)
\(1 \oplus (1 \oplus 1) =1 \oplus 0 = 1\)
\((1 \oplus 1) \oplus 0 =0 \oplus 0 = 0\)
\(1 \oplus (1 \oplus 0) =1 \oplus 1 = 0\)
\((1 \oplus 0) \oplus 1 =1 \oplus 1 = 0\)
\(1 \oplus (0 \oplus 1) =1 \oplus 1 = 0\)
\((1 \oplus 0) \oplus 0 =1 \oplus 0 = 1\)
\(1 \oplus (0 \oplus 0) =1 \oplus 0 = 1\)
\((0 \oplus 1) \oplus 1 =1 \oplus 1 = 0\)
\(0 \oplus (1 \oplus 1) =0 \oplus 0 = 0\)
\((0 \oplus 1) \oplus 0 =1 \oplus 0 = 1\)
\(0 \oplus (1 \oplus 0) =0 \oplus 1 = 1\)
\((0 \oplus 0) \oplus 1 =0 \oplus 1 = 1\)
\(0 \oplus (0 \oplus 1) =0 \oplus 1 = 1\)
\((0 \oplus 0) \oplus 0 =0 \oplus 0 = 0\)
\(0 \oplus (0 \oplus 0) =0 \oplus 0 = 0\)
3つ目
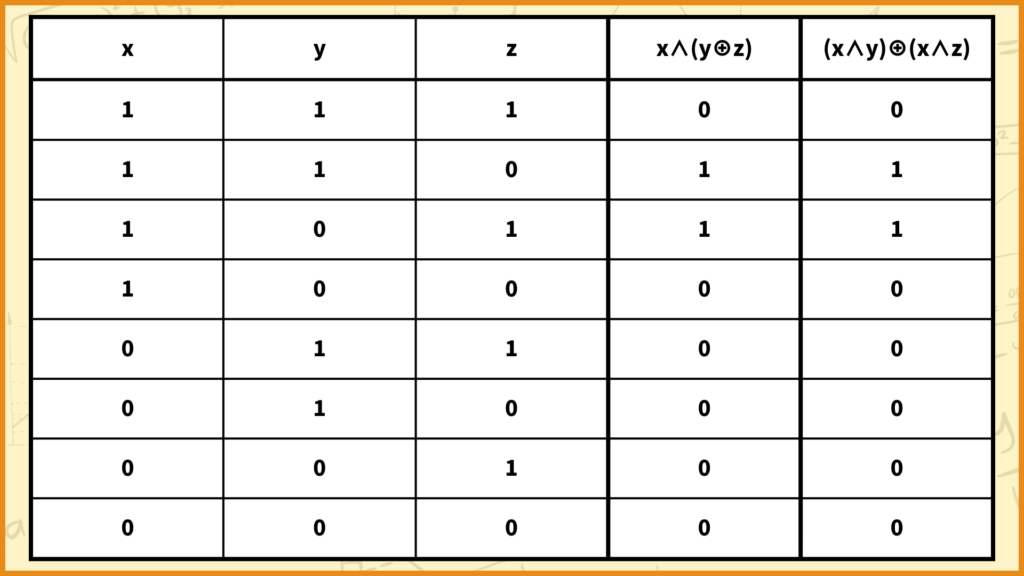
3つ目：\(x \wedge (y \oplus z) = (x \wedge y) \oplus (x \wedge z)\)
上の表の右側の列2つを計算すると\(x \wedge (y \oplus z) = (x \wedge y) \oplus (x \wedge z)\)が成り立つのが分かります。
この性質は分配律と呼ばれます。
\(1 \wedge (1 \oplus 1) = 1 \wedge 0 = 0\)
\((1 \wedge 1) \oplus (1 \wedge 1) = 1 \oplus 1 = 0\)
\(1 \wedge (1 \oplus 0) = 1 \wedge 1 = 1\)
\((1 \wedge 1) \oplus (1 \wedge 0) = 1 \oplus 0 = 1\)
\(1 \wedge (0 \oplus 1) = 1 \wedge 1 = 1\)
\((1 \wedge 0) \oplus (1 \wedge 1) = 0 \oplus 1 = 1\)
\(1 \wedge (0 \oplus 0) = 1 \wedge 0 = 0\)
\((1 \wedge 0) \oplus (1 \wedge 0) = 0 \oplus 0 = 0\)
\(0 \wedge (1 \oplus 1) = 0 \wedge 0 = 0\)
\((0 \wedge 1) \oplus (0 \wedge 1) = 0 \oplus 0 = 0\)
\(0 \wedge (1 \oplus 0) = 0 \wedge 1 = 0\)
\((0 \wedge 1) \oplus (0 \wedge 0) = 0 \oplus 0 = 0\)
\(0 \wedge (0 \oplus 1) = 0 \wedge 1 = 0\)
\((0 \wedge 0) \oplus (0 \wedge 1) = 0 \oplus 0 = 1\)
\(0 \wedge (0 \oplus 0) = 0 \wedge 0 = 0\)
\((0 \wedge 0) \oplus (0 \wedge 0) = 0 \oplus 0 = 0\)
4つ目～7つ目
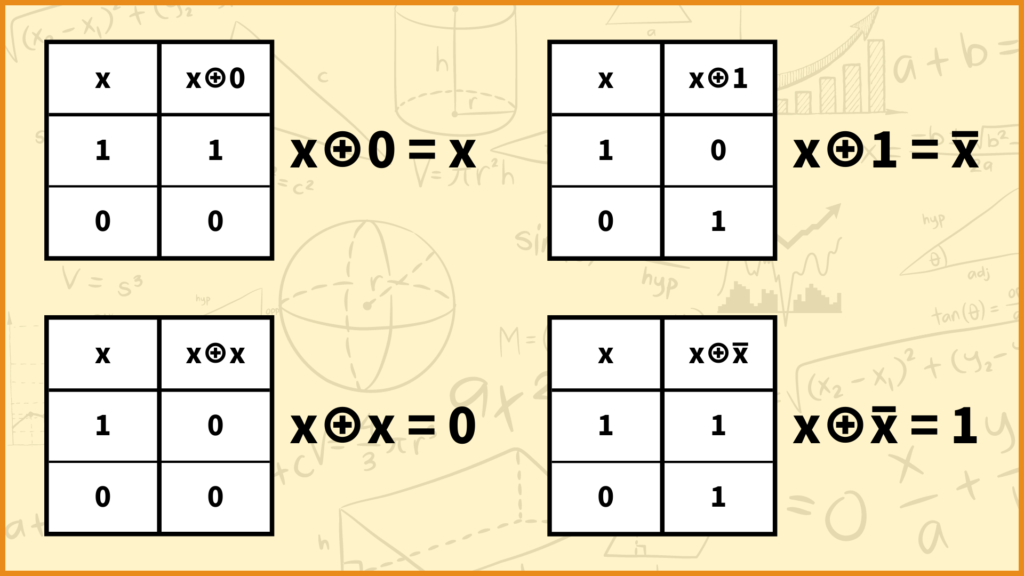
4つ目：\(x \oplus 0 = x\)
5つ目：\(x \oplus 1 = \bar{x}\)
6つ目：\(x \oplus x = 0\)
7つ目：\(x \oplus \bar{x} = 1\)
これも1と0を代入するとすぐに分かりますね。
おわりに
いかがでしたか。
今回の記事では排他的論理和（EXOR）について解説していきました。
今後もこのような論理関数に関する記事を書いていきます！
最後までこの記事を読んでくれてありがとうございました。
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください！
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます！
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学（けいえいこうがく、英: engineering management）は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
