こんにちは!しゅんです!
今回はヒープソートについて解説していきます!
データを分析するときに小さい順に数字を並べる操作は頻繁に行います。そんなときに使うのがヒープソートという手法です。
この記事ではヒープソートというアルゴリズムについて、基本的な考え方や実装方法を分かりやすく解説していきます。
また今回はpythonを使って実際にヒープソートを実装していきたいと思います。
それでは解説していきましょう!
以前の記事でマージソートについて説明しました。こちらもぜひ見てみてください!
普段はNBAのデータ分析をしたりしています。
ぜひこちらの記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
ヒープってなに?
ヒープソートをするためにヒープというデータ構造を使います。これは枝みたいな構造をしており、二分木(Binary Tree)の一種です。図を使って説明します。
例えばある数列\(A = [5,6,2,3,1,4]\)をヒープで表すと下のようになります。
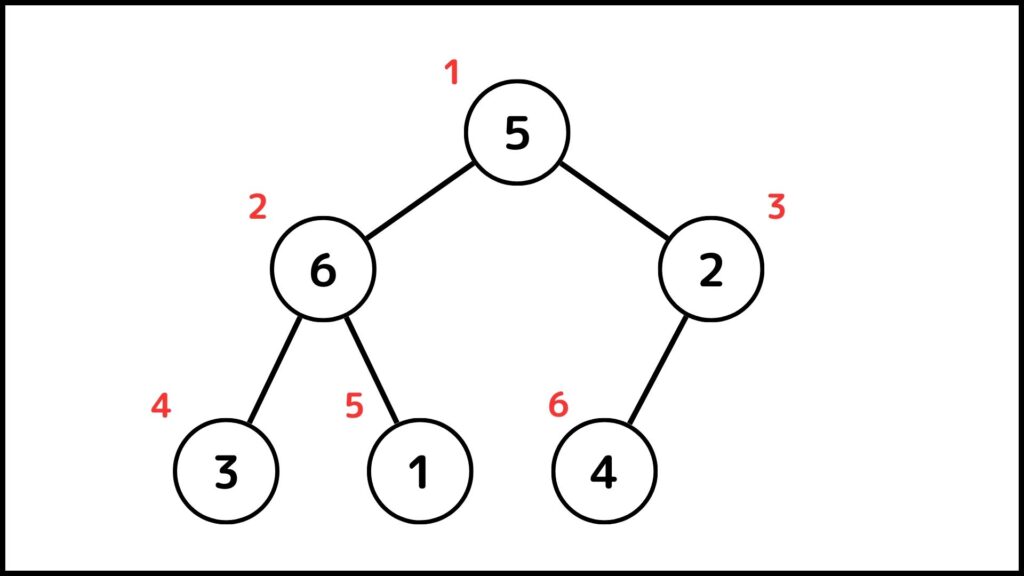
ヒープソートでは例えば3と1は6の子、また6は3と1の親と呼びます。他にも例えば5の子は6と2で4の親は2となります。二分木は一つの点に関してその子が最大でも2個までの木のことを表します。
ヒープでは数列の最初の数字を一番上の親として枝を伸ばしていきます。例えば下のような二分木はヒープとはなりません。
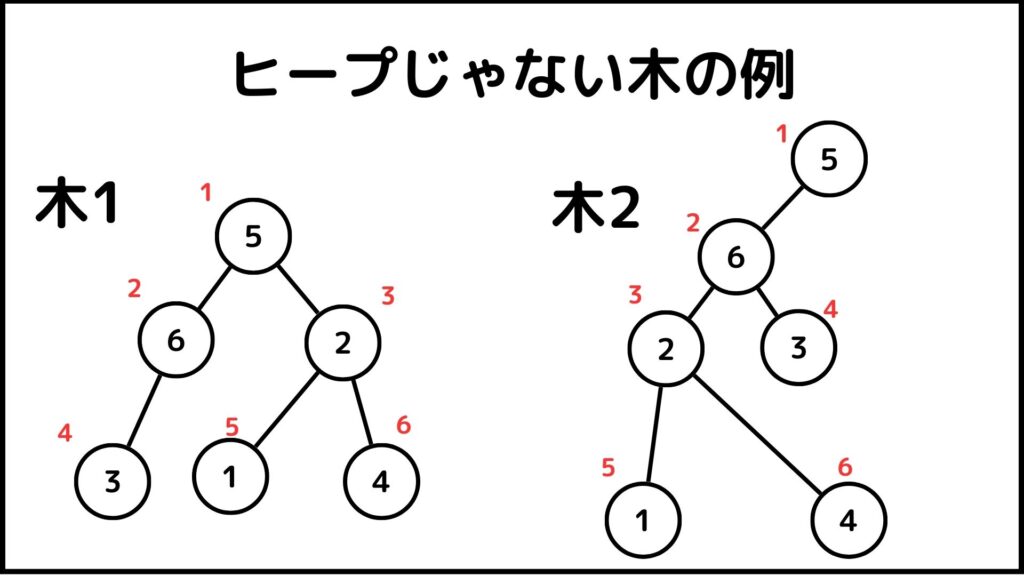
上の2つの木はどちらもヒープではありません。ヒープは以下の2つの条件を満たす二分木である必要があります。
- 一番下の層ができるだけ左に詰まっている
- 一番下の層以外の層がすべて埋まっている
例えば木1を見てください、これは条件①に反しています。ヒープは一番下の層が左に寄っていますが木1はそうではないですね。ヒープにするためには6から1に枝が伸びている必要があります。
次に木2を見てください、これは条件②に反しています。ヒープは最下層以外の層がすべて埋まっている必要がありますが木2はそうではありません。本来ならば5の子が2つなければヒープになりませんが子が1個しかありません。
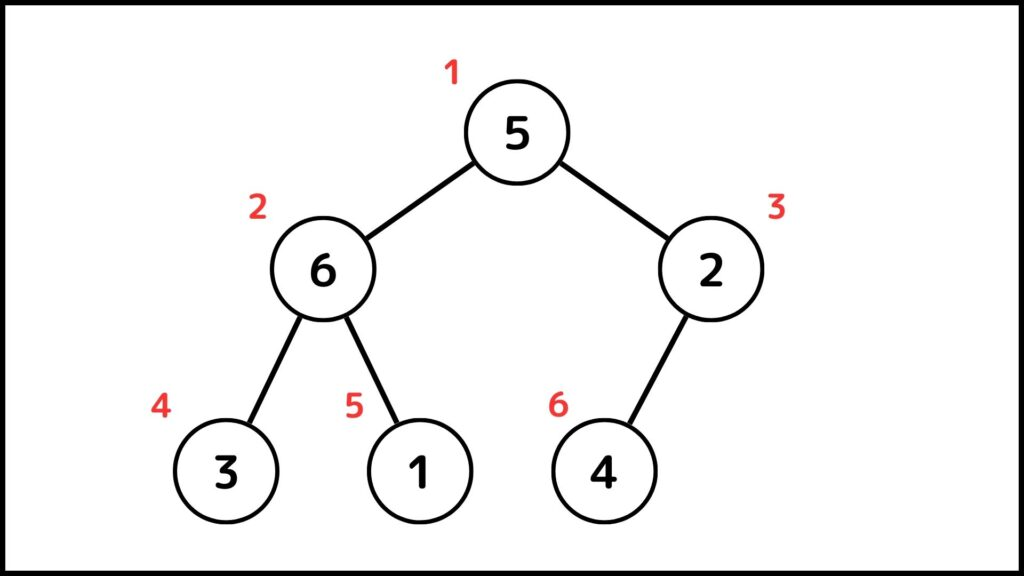
ヒープソートをするためには、これらの条件を満たすような二分木を考える必要があります。
ヒープソートの基本的な考え方
ここからはヒープソートのアルゴリズムの解説をしていきたいと思います。ヒープソートはざっくり2つのステップに分けることができます。それでは1つずつ解説していきましょう。
STEP. 1
STEP. 1は先ほど説明したヒープを組み替える操作をします。なぜこのような組み替えをするのかは後で説明するので、まずは組み替えの手順の説明をしていきます。
- ある数字に着目する
- 着目した数字がその子の数字よりも小さかったら子の中で数字が大きい方と位置を交換する
- 着目した数字がその子以上になる、または最下層にたどり着くまで操作2を続ける
そうでなければ操作を終了する
さきほどのヒープを使って説明していきます。例えば5に着目して上の操作をやってみます。5の子は6と2なので、5と6の位置を入れ替えます。
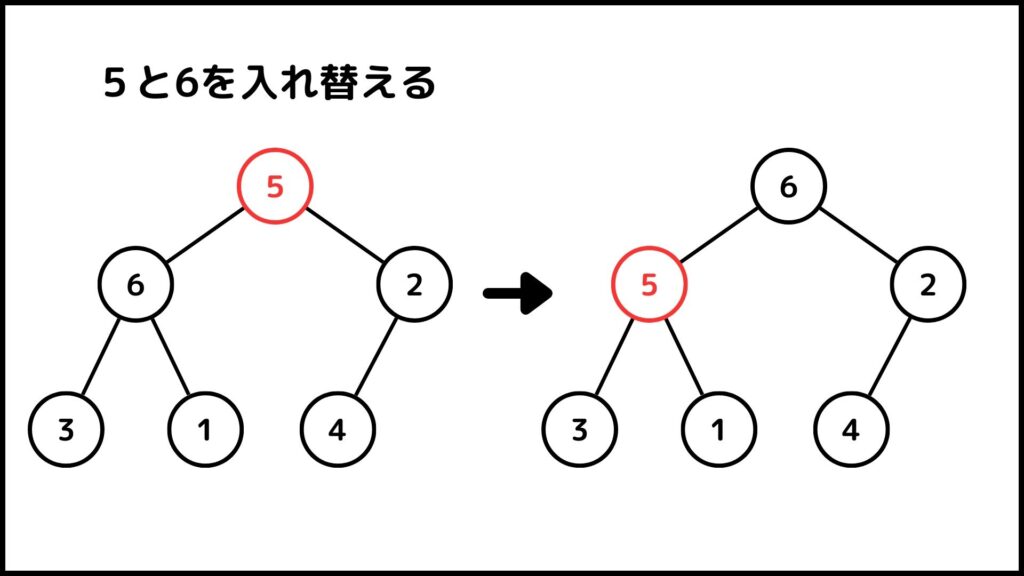
もう一度5に着目してみましょう。今度は3と1が子になりますが、どちらも5よりは小さいですね。ということで操作を終了します。
今度は下のヒープに対して子の操作をしてみましょう。
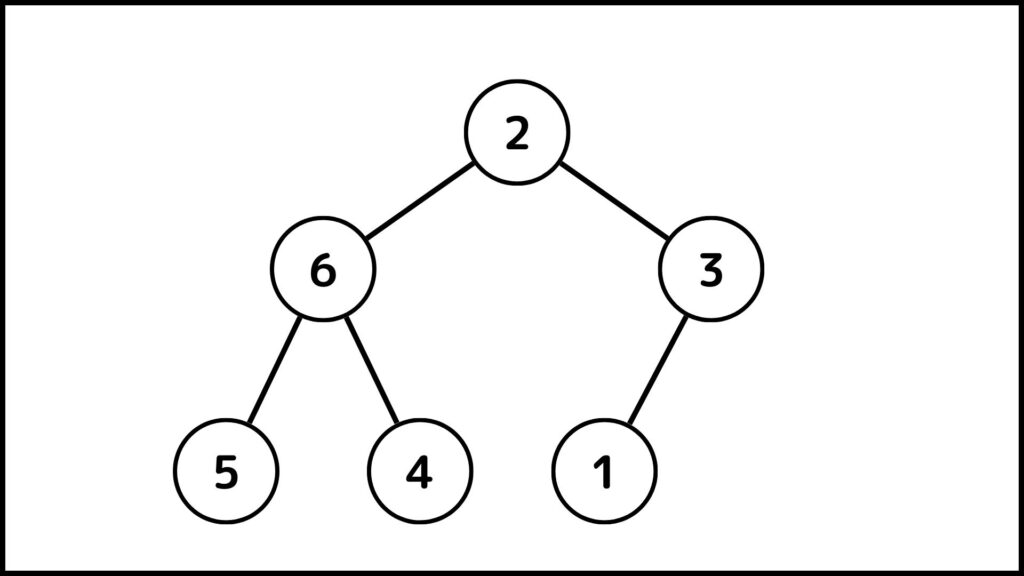
2に着目して上記の操作をしていきます。2の子は6と3なので2と6を交換します。
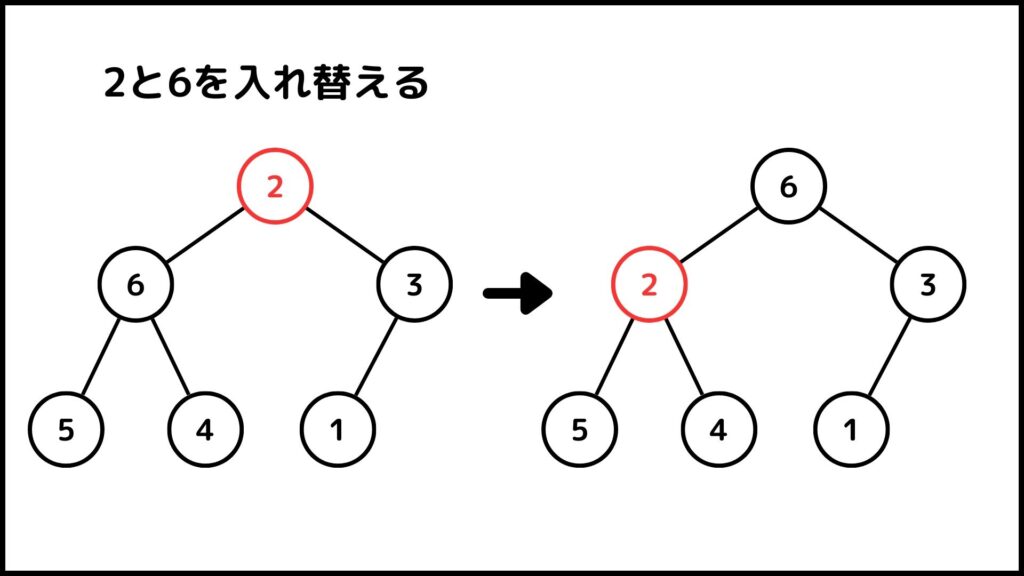
もう一度2に着目してみましょう。今度は2の子が5と4になりました。よって2と5を入れ替えましょう。
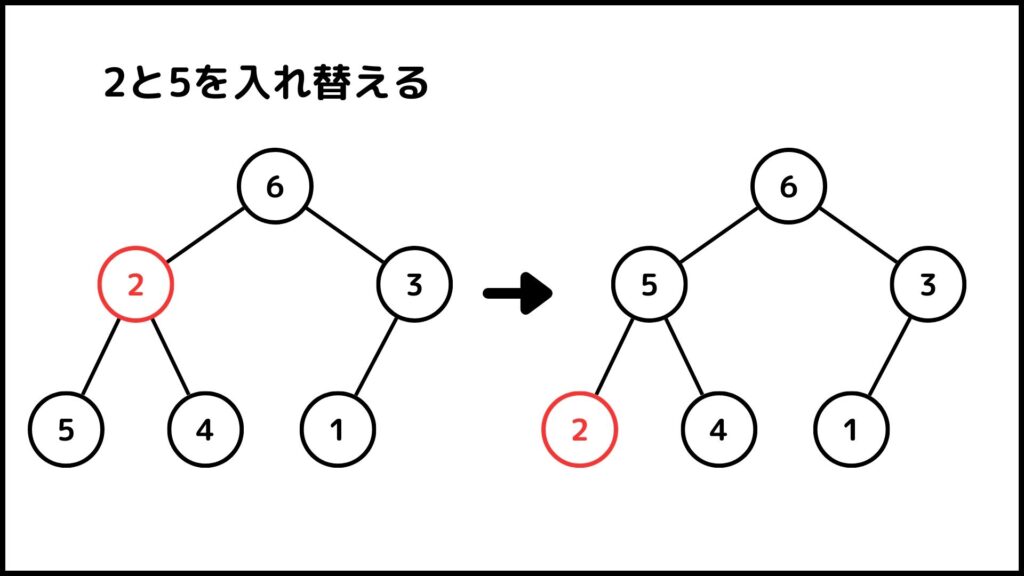
この時点で2が最下層に移りました。ということで操作を終了します。
STEP. 2
STEP. 2ではSTEP. 1の操作を数列の中の半分の数字に対して実行します。例えば数列が\(A = [6,5,3,2,4,1]\)とすると6, 5, 3に対してSTEP. 1の操作を適用します。このときに3, 5, 6の順番でSTEP. 1を実施してください。
数列の要素数が奇数の場合は切り捨てて計算してください。例えば数列が\(A = [7,6,5,3,2,4,1]\)の場合は7, 6, 5に対してSTEP. 1の操作を適用します。
数列\(A = [2,4,1,5,6,3]\)に対してSTEP. 2を適用する様子を説明していきます。まず1に着目してSTEP. 1を実施します。1の子は3なので1と3を交換しましょう。この時点で1が最下層に到達したので操作を終了します。
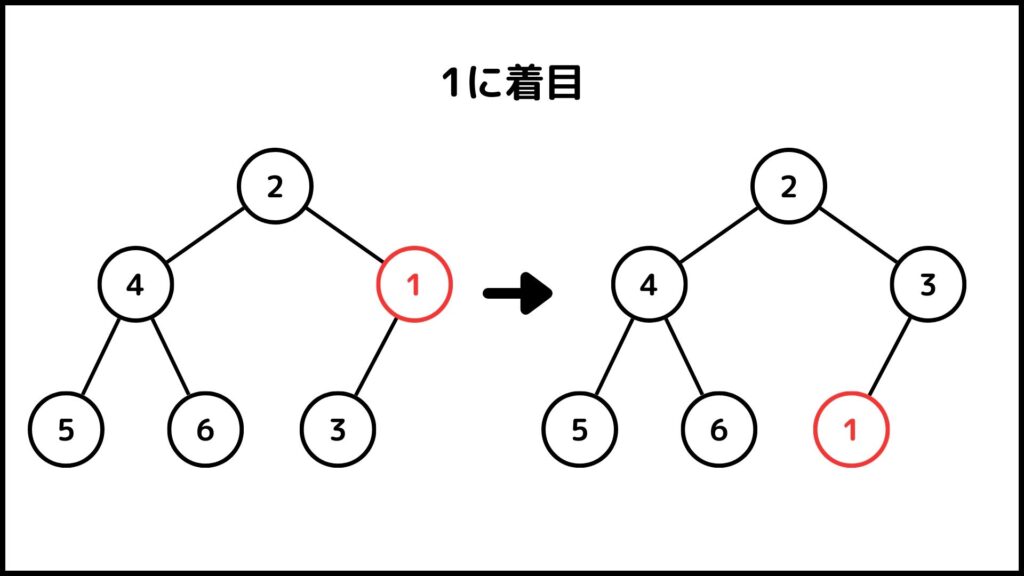
次に4に着目します。4の子は5と6なので4と6を交換します。この時点で4が最下層に到達したので操作を終了します。
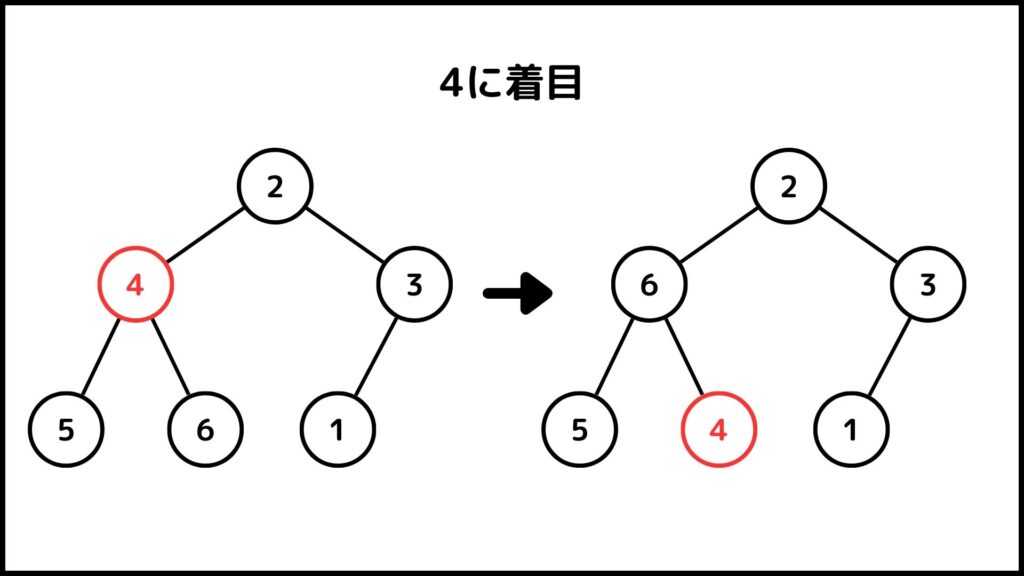
最後に2に着目しましょう。2の子は6と3なので2と6を交換します。もう一度2に着目しましょう。2の子は5と4なので2と5を交換します。この時点で2が最下層に到達したので操作を終了します。
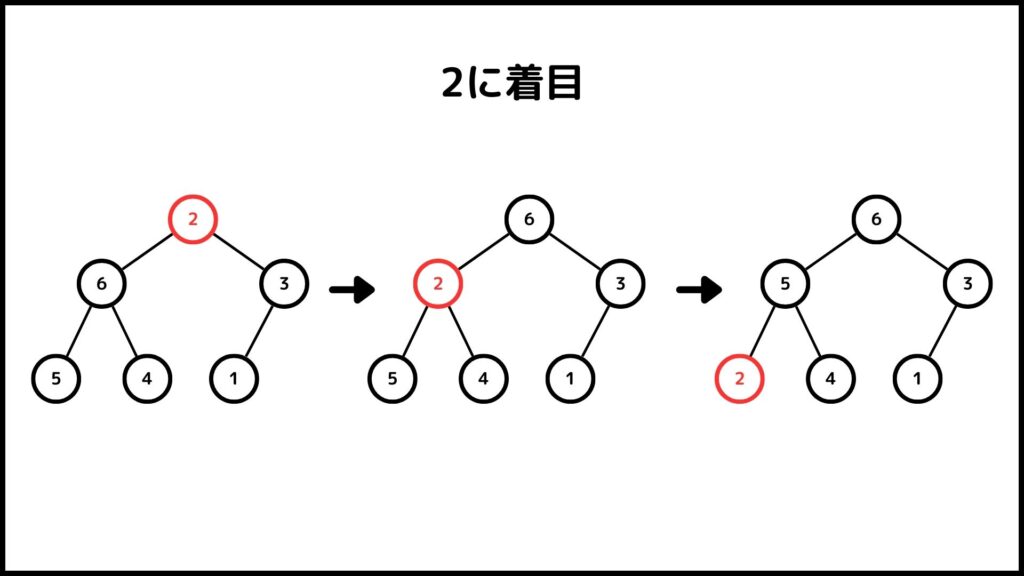
以上でSTEP. 2が終了しました。
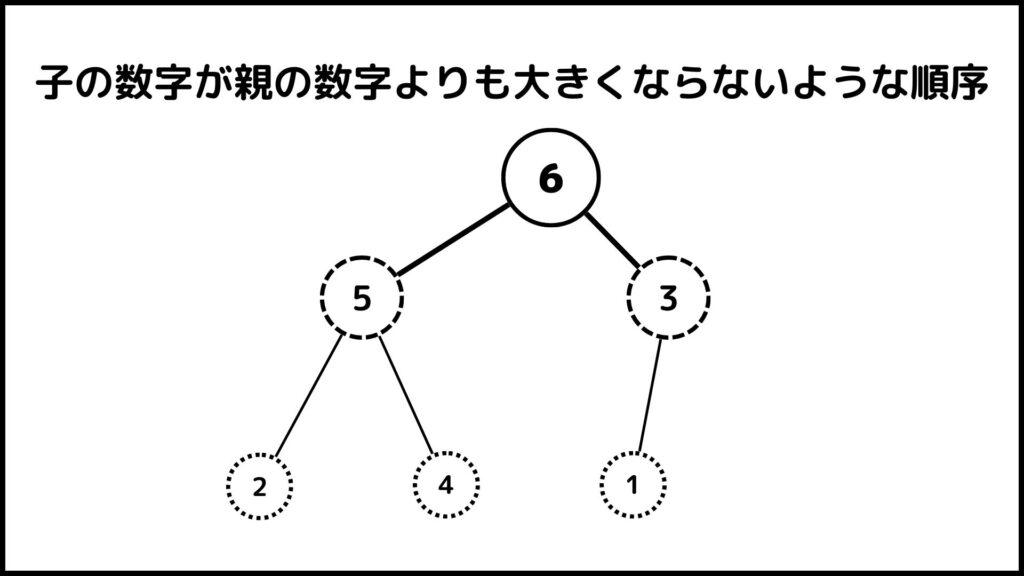
最後になぜこのような操作をするのかを説明したいと思います。この操作をすることによって子の数字が親の数字よりも必ず大きくならないように組み替えることができています。このような順序に組み替えることによって、最終的にソートをする際に非常に便利になります。
ヒープソートの実装方法
先ほど説明した2つのステップを使ってヒープソートを実装していきます。以下がヒープソートの手順となります。その際、数字列を\(A\)、数字列の要素数を\(n\)として話を進めていきます。
- STEP. 2を実行する
- \(iがnから2まで以下の操作を行う\)
・\(A[1]とA[i]を交換する\)
・\(Aの大きさをi-1にしてi番目の数字を切り離す\)
・\(1に着目してSTEP. 1を実行する\) - Aを返す
文字で説明しても分かりにくいので具体例を用いてヒープソートがどうなっているかについて説明していきます。数列\(A = [2,4,1,5,6,3]\)に対してヒープソートを適用していきます。
まずSTEP. 2を実行します。STEP. 2の説明で用いた数列と同じなのでその結果を見ると\(A=[6,5,3,2,4,1]\)となります。
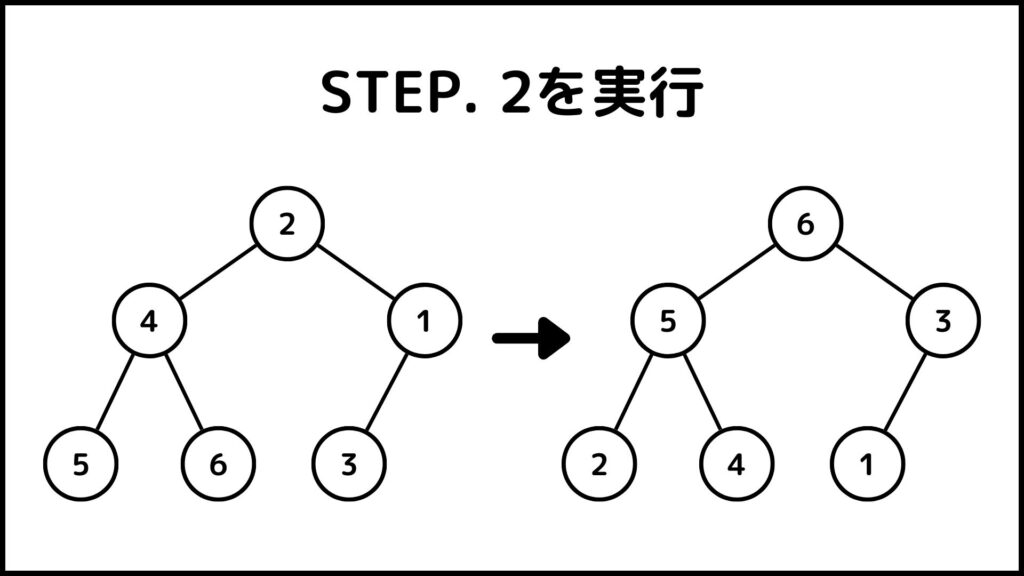
要素数が6なので、次に\(i=n=6\)として2番目の操作を1つずつ実行していきます。まず\(A[1]\)と\(A[6]\)を交換します。そして\(A\)の大きさを6から5にして6を切り離します。
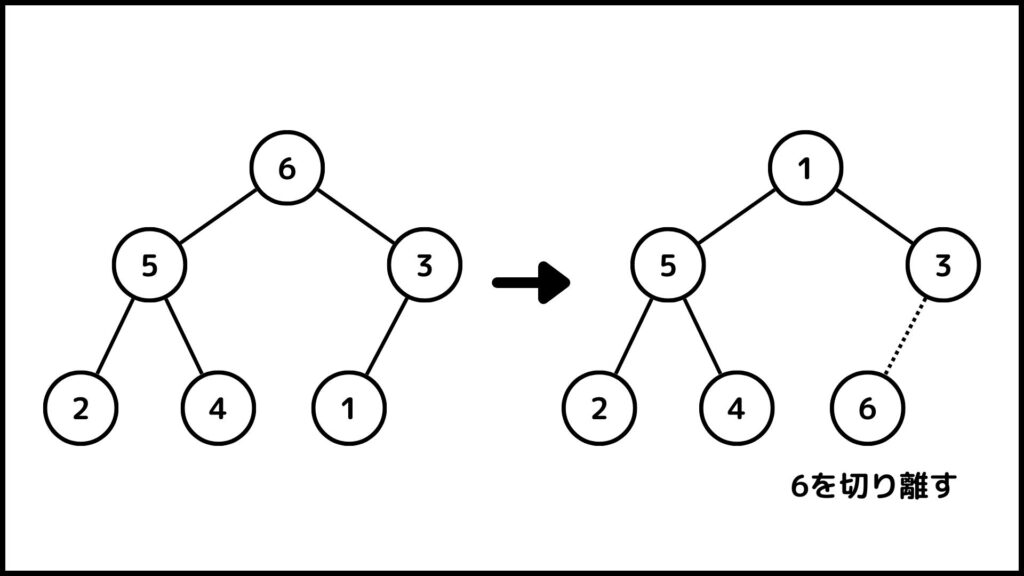
6を切り離した状態で1番目の数字に着目してSTEP. 1を実行します。その結果が下の図です。
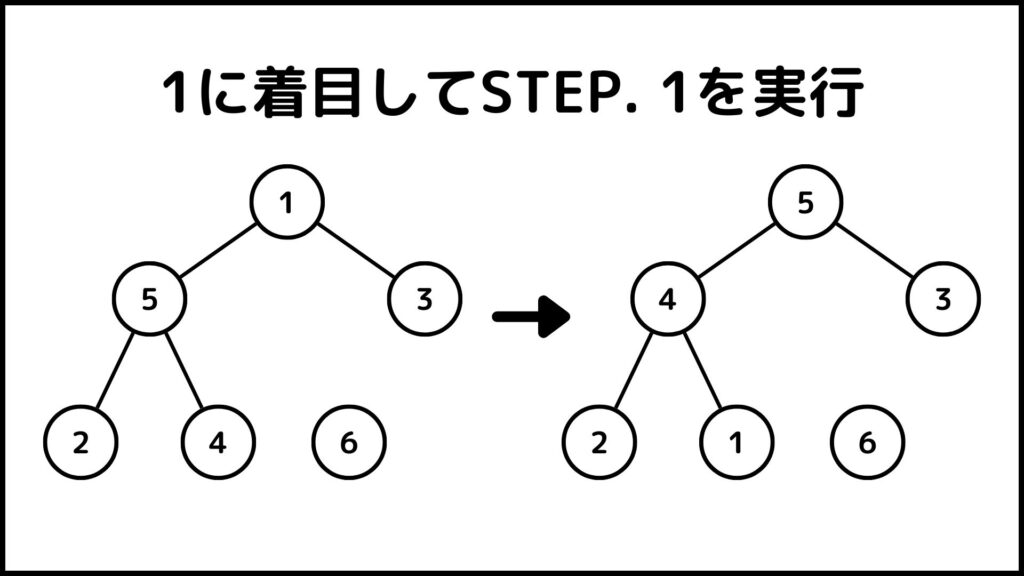
ここまでできたら\(i=5\)にしてもう一度同じ操作をします。ここからは1枚のスライドにまとめて実行結果を表します。
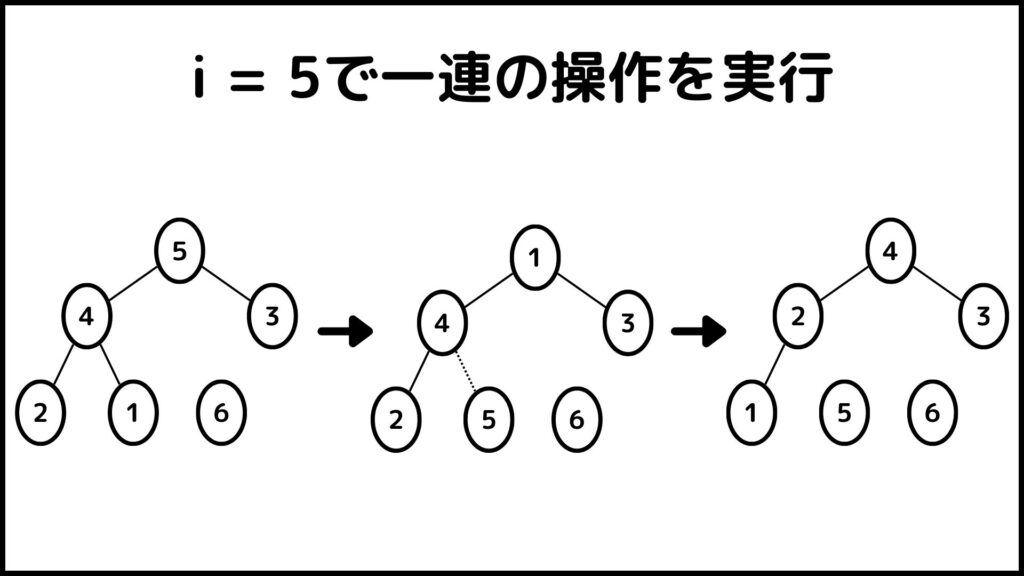
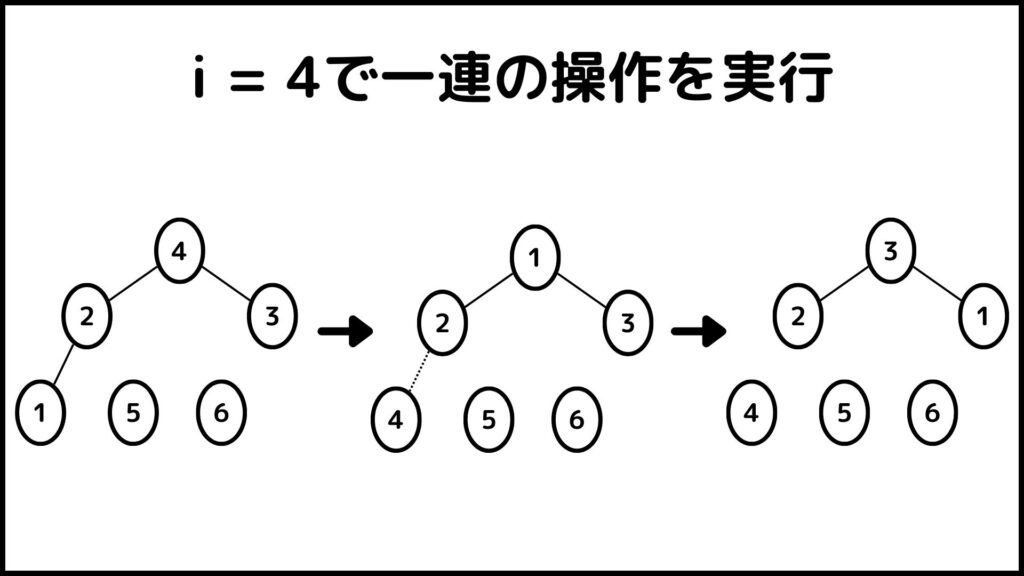
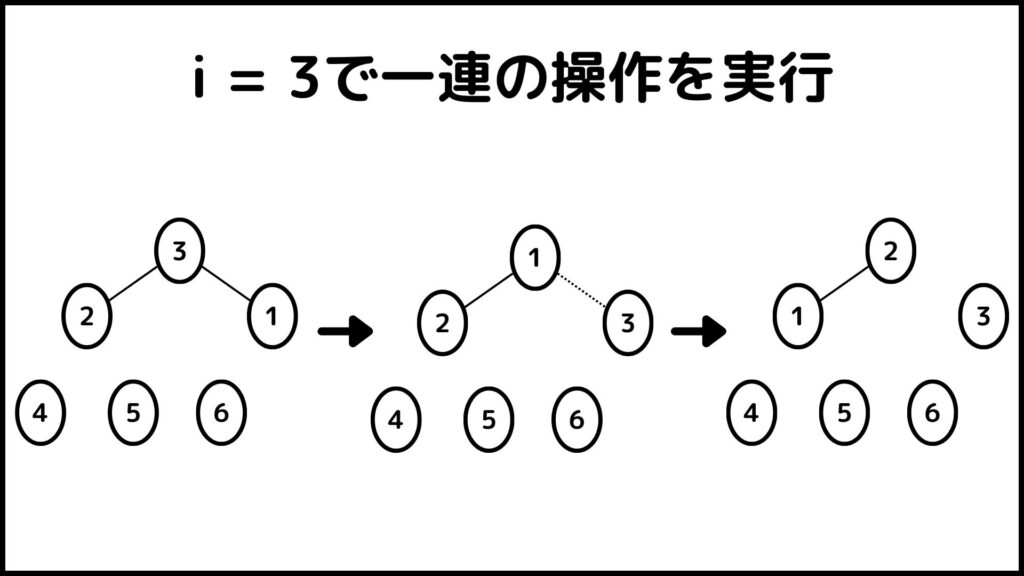
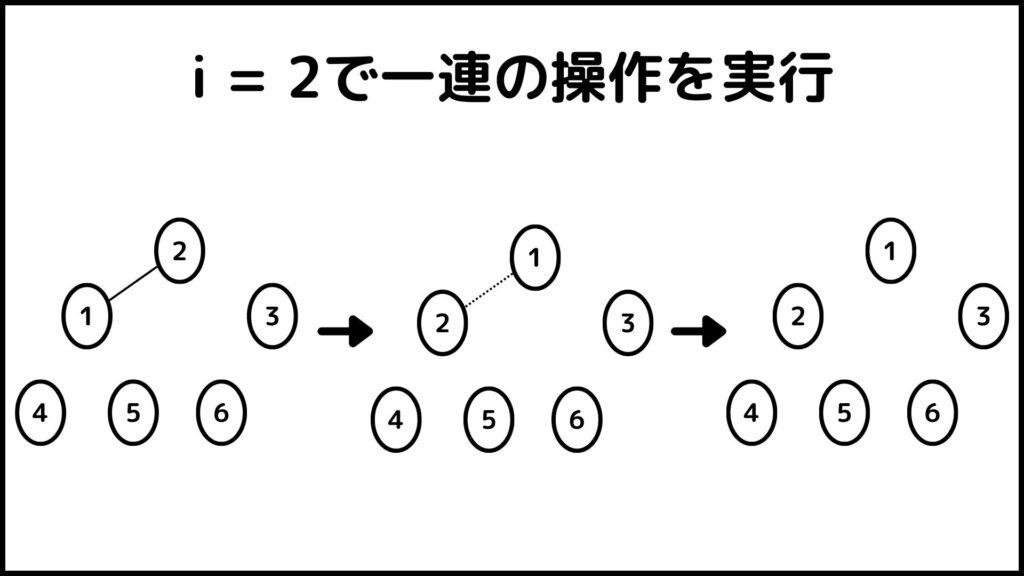
ということで\(i\)が\(n\)から\(2\)まで操作を実行しました。ということで最後に出来上がった数字列\(A\)を見てみるとちゃんと\(A=[1,2,3,4,5,6]\)となっていますね。
ヒープソートは計算量が少ない
今回は簡単にするために6つの数字列を使って説明しましたが、これは要素数が大きくなっても使えます。そしてこのヒープソートは要素数が大きくなればなるほど有用性が高くなります。
なぜならヒープソートは普通のソートに比べて計算量が少なくて済むからです。ここからは少し難しい話になります。
数字を小さい順に並べるソートにはバブルソート、選択ソート、クイックソート、挿入ソートなどたくさんの種類がありますが、どれを使えば良いかの指標に計算量というものがあります。
計算量とはあるアルゴリズムを使ったときにだいたいどれくらい時間がかかるかを評価したもので、これが小さければ小さい程良いアルゴリズムだと言われます。
普通のソートの計算量は\(O(n^2)\)ですが、ヒープソートの計算量は\(O(nlogn)\)となります。計算量の表記を説明するとそれだけで1つの記事が書けそうなので今回は省略します。ヒープソートの方が早く計算できると思ってください。
ヒープソートをpythonで実装してみる
最後にヒープソートをpythonで実装してみます。以下がヒープソートを実行するためのコードになります。
# ヒープソートを定義する
def heap_sort(arr):
# ヒープを構築する
build_max_heap(arr)
# 1つずつ要素を取り出し、ヒープを再構築することでソートする
for i in range(len(arr)-1, 0, -1):
arr[0], arr[i] = arr[i], arr[0]
max_heapify(arr, 0, i)
return arr
# STEP. 1を定義する
def max_heapify(arr, i, n):
left = 2*i+1
right = 2*i+2
largest = i
# 左の子ノードが親ノードより大きい場合
if left < n and arr[left] > arr[largest]:
largest = left
# 右の子ノードが親ノードより大きい場合
if right < n and arr[right] > arr[largest]:
largest = right
# 最大値が変更された場合は、再帰的にヒープを構築する
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
max_heapify(arr, largest, n)
# STEP. 2を定義する
def build_max_heap(arr):
n = len(arr)
for i in range(n//2-1, -1, -1):
max_heapify(arr, i, n)pythonでは数字列の数え方(インデックス)が0, 1, 2, …なので若干修正が必要ですが、やっていることはこれまでに説明したことです。実際にソートできるか確かめてみましょう。
A = [4,3,6,5,8,9,7,1,2]
heap_sort(A)
ということでちゃんとソートできましたね。
おわりに
いかがでしたか。
今回の記事ではヒープソートについて解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。




