- 利得行列ってなに？
- 強支配、弱支配ってなに？
- 戦略の逐次消去のやり方が知りたい…
こんにちは！しゅんです！
今回は戦略の逐次消去について解説していきます！
逐次消去はゲーム理論で登場する用語です。この記事では逐次消去について図を使ってなるべく分かりやすく解説します。
また逐次消去を理解するためには利得行列や強支配、弱支配についても知っておく必要があるのでそれらも解説したいと思います！
それでは解説していきましょう！
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください！
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます！
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学（けいえいこうがく、英: engineering management）は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
利得行列ってなに？
戦略の逐次消去の説明をするためにまず利得行列の説明からする必要があります。
非協力ゲーム理論でよく登場する行列がありますよね。プレイヤー1と2がそれぞれある戦略を取ることによってどれくらいの利得を得られるかを行列にしたやつです。
例えば下の問題をこの行列に直してみましょう。
プレイヤー1と2がじゃんけんを行う。
・じゃんけんに勝てば利得は1
・じゃんけんに負ければ利得は-1
・じゃんけんにあいこだったら利得は0
上の行列が今回の問題を利得行列で表したものになります。例えばプレイヤ―1がチョキ、プレイヤー2がパーを出したらそれぞれの利得は1と-1になるので1,-1と書かれています。
視覚的に分かりやすいのでこの行列はよく使います。
強支配と弱支配ってなに？
次に強支配と弱支配について説明したいと思います。
強支配
強支配を簡単に説明すると、
「相手がどんな戦略を取っても自分はこの戦略を取れば必ず得するっていう状態」
のことです。下の具体例を使ってもっと詳しく説明します。
もしプレイヤー2が戦略1を取ったときプレイヤー1はどのような戦略を取るのが合理的でしょうか。プレイヤー1は戦略1を取れば自身の利得は0、戦略2を取れば自身の利得は1となりますね。
ということはプレイヤー2が戦略1を取った場合プレイヤー1は戦略2よりも戦略1を取るのが良いはずです。
同じようにプレイヤー2が戦略2,3を取った場合を考えてみると、どちらの場合でもプレイヤー1は戦略1より戦略2を取った方が必ず利得が大きくなります。
このような状態のとき、「戦略1は戦略2に強支配される」と言います。
プレイヤー1は戦略1よりも戦略2を取る方が合理的だよねってことです。
弱支配
強支配を簡単に説明すると、
「相手がどんな戦略を取っても自分はこの戦略を取ったら必ず損しないっていう状態」
のことです。下の具体例を使ってもっと詳しく説明します。
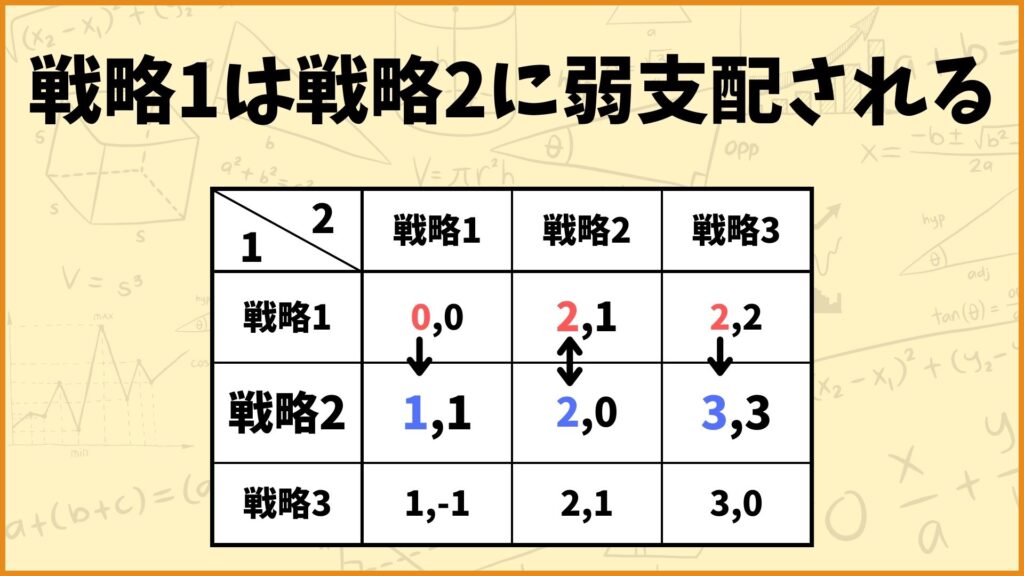
先ほどと同じように見ていきましょう。プレイヤー2が戦略1を取ったとき、プレイヤー1は戦略2を取った方が利得が大きくなりますね。戦略3に間しても同様です。
しかしプレイヤー2が戦略2を取った時はどうでしょう。プレイヤー1は戦略1をとっても戦略2を取っても自身の利得が変わりません。このような場合戦略2は戦略1に弱支配されると言います。
強支配はイコールを認めないので今回の場合は強支配とはなりません。一方で弱支配はイコールを認めるので今回の場合でもOKです。
プレイヤー1の戦略2と戦略3のように相手がどの戦略をとっても自身の利得が変わらない場合は弱支配されるとは言いません。弱支配するためには少なくとも1つの戦略においては利得が大きい必要があります。
戦略の逐次消去ってなに？
いよいよ戦略の逐次消去の説明をしたいと思います。戦略の逐次消去を簡単に説明すると、
「支配される戦略を1つずつ消去して合理的な戦略を求めること」
です。強支配を例にして上の問題を使って説明したいと思います。
まず最初にプレイヤー1の戦略を見ると、戦略1が戦略2に強支配されていますね。合理的に考えるとプレイヤー1は戦略1を取らないはずです。ということでプレイヤー1の戦略1を消去します。
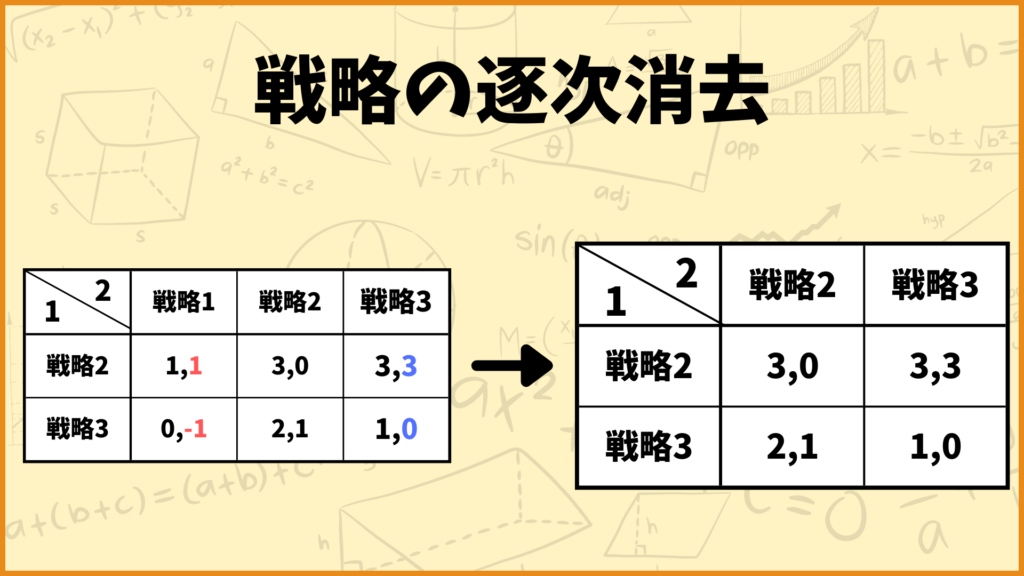
次にプレイヤー2の戦略を見てみると、戦略1が戦略3に強支配されていますね。合理的に考えるとプレイヤー2は戦略1を取らないはずです。ということでプレイヤー2の戦略1を消去します。
プレイヤー1の戦略を見てみると、戦略3が戦略2に強支配されていますね。合理的に考えるとプレイヤー1は戦略3を取らないはずです。ということでプレイヤー1の戦略3を消去しましょう。
プレイヤー2の戦略を見てみると、戦略2が戦略3に強支配されていますね。合理的に考えるとプレイヤー2は戦略2を取らないはずです。ということでプレイヤー2の戦略2を消去しましょう。
このように支配される戦略を1つずつ消去していくことを逐次消去と言います。最終的に残った戦略の組（プレイヤー1は戦略2、プレイヤー2は戦略3）は合理的な戦略と言えますね。
戦略の逐次消去のやり方は2種類ある
戦略の逐次消去のやり方は2種類あるのでそれぞれ説明したいと思います。
1つずつ戦略を消去
1つ目のやり方は先ほどやったように戦略を1つずつ消去していく方法です。
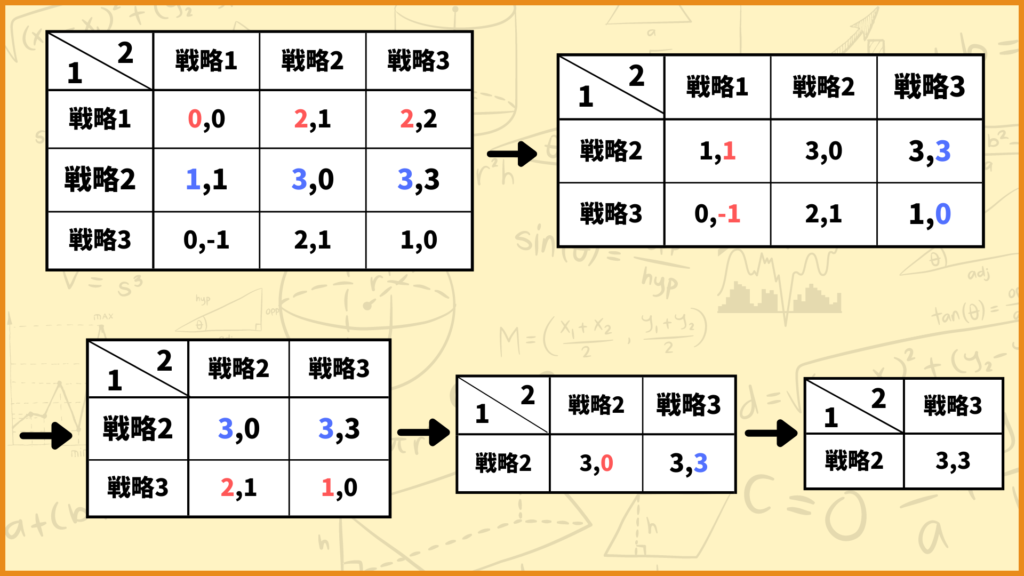
まとめて戦略を消去
2つ目のやり方はまとめて戦略を消去する方法です。さきほどと同じ問題を使って説明します。
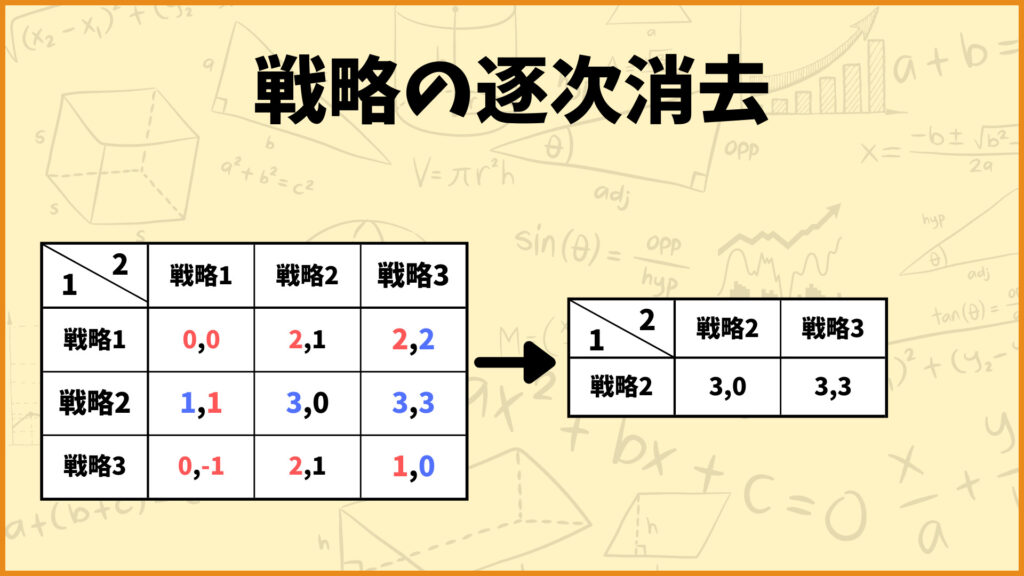
プレイヤー1の戦略を見ると戦略1が戦略2に強支配されていますね。1つ目のやり方ではこの時点で戦略2を消去して次のステップに進みました。
しかしプレイヤー1の戦略をよく見てみると実は戦略3も戦略2に強支配されていますね。さらにプレイヤー2の戦略を見てみると戦略1が戦略3に強支配されていることが分かります。
2つ目のやり方ではこれらの戦略をまとめて消去します。
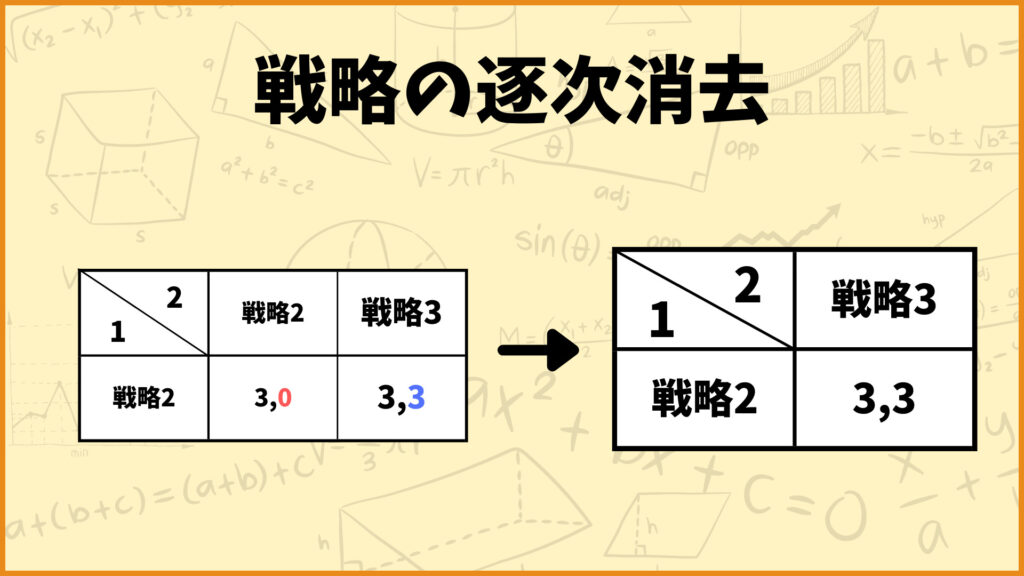
次にプレイヤー2の戦略見てみると戦略2が戦略3に強支配されているので戦略2を消去します。ということで今回の問題の場合は1つ目と2つ目の逐次消去の結果得られる戦略の組が同じになりました。
このように2つの逐次消去で得られる結果はいつでも同じなのでしょうか？
2つのやり方で何が変わるの？
強支配の場合
強支配される戦略を消去していく場合1つ目の逐次消去のやり方と2つ目の逐次消去のやり方で得られる結果は一致することが知られています。
弱支配の場合
弱支配される戦略を消去していく場合1つ目の逐次消去のやり方と2つ目の逐次消去のやり方で得られる結果が違う場合があります。
例えば下の例を見てみましょう。
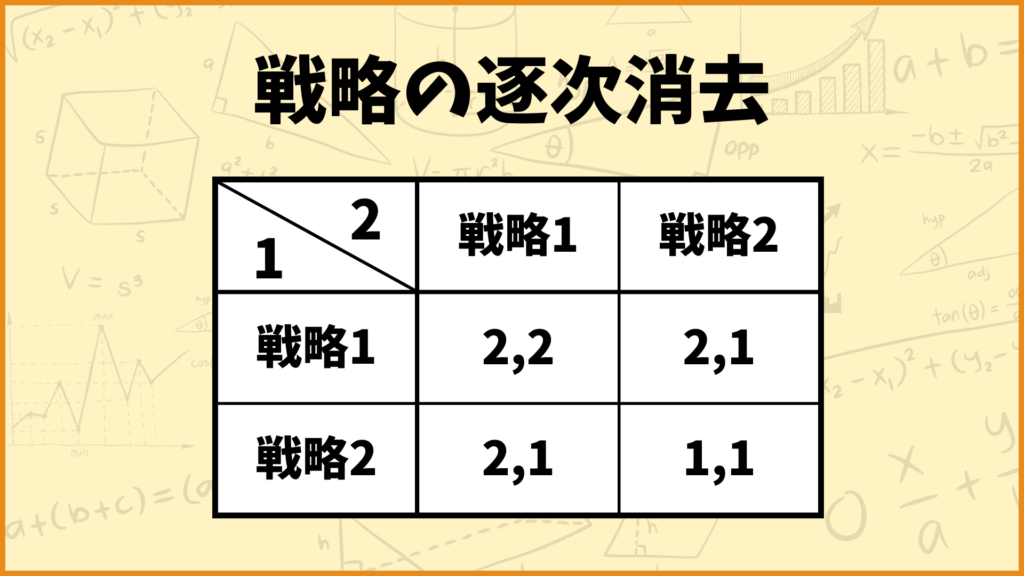
まずは1つ目のやり方で逐次消去をしていきましょう。プレイヤー2の戦略を見てみると戦略2が戦略1に弱支配されていることが分かります。ということで戦略2を消去しましょう。
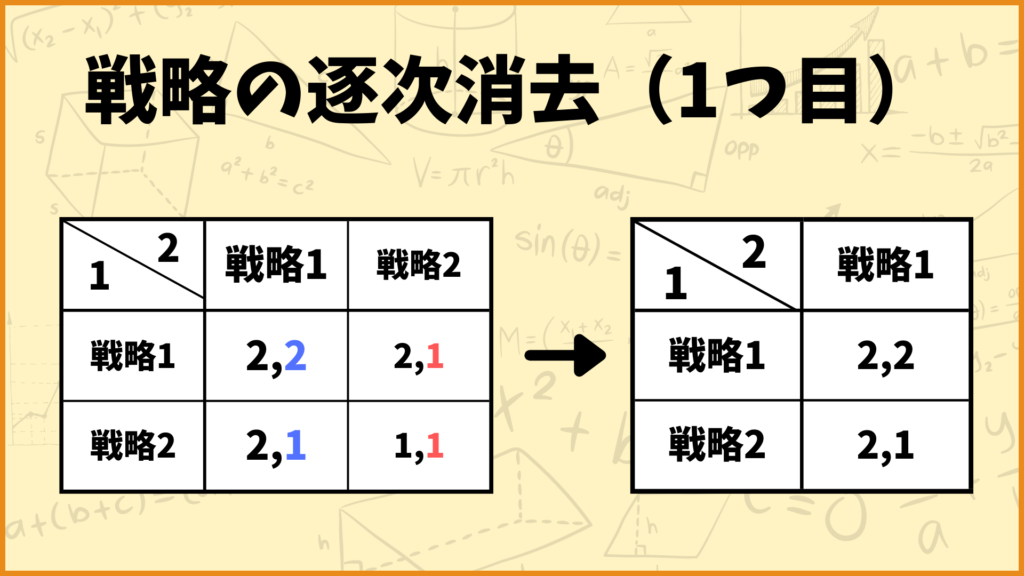
実はこの時点でもう弱支配される戦略がありません。ということで1つ目の逐次消去をした結果は上のようになります。
次に同じ問題に対して2つ目のやり方で逐次消去を行っていきましょう。
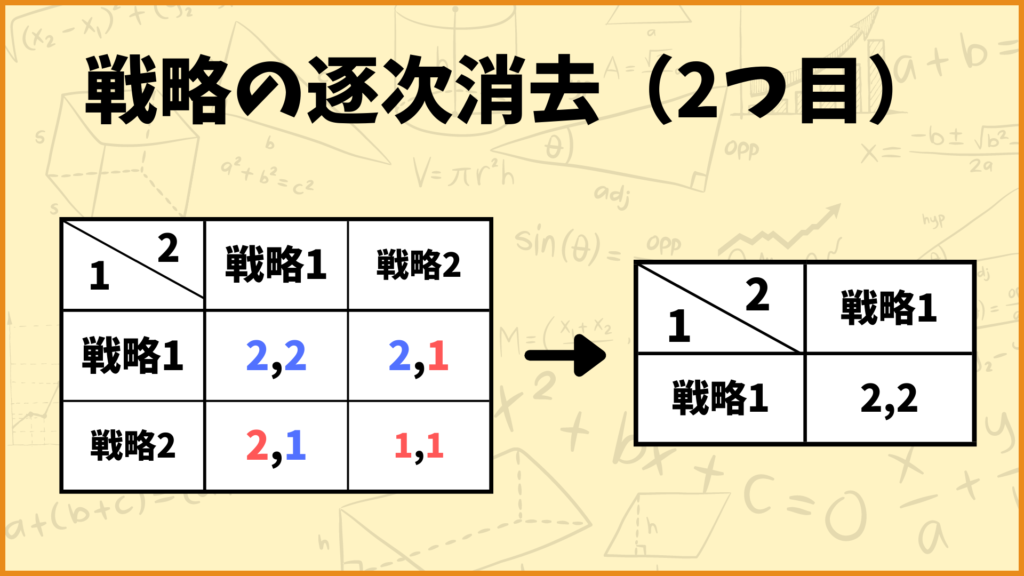
プレイヤー2を見ると戦略2が戦略1に弱支配されていることは1つ目のから分かりました。それに加えてプレイヤー1を見ると戦略2が戦略1に支配されていますね。ということで両方消去しましょう。
2つ目の逐次消去を行うと残った戦略の組は上の図のようになりました。これは1つ目の結果とは異なりますね。
このように弱支配の場合は1つ目の方法と2つ目の方法で得られる結果が異なる場合があります。
おわりに
いかがでしたか。
今回の記事では戦略の逐次消去について解説していきました。
今後もこのような経営工学に関する記事を書いていきます！
最後までこの記事を読んでくれてありがとうございました。
