こんにちは!しゅんです!
中学の数学を勉強すると下のような公式を覚えさせられます。
\((x+a)(x+b) = x^2 + (a+b)x + ab\)
\((x+a)^2 = x^2 + 2ax + a^2\)
\((x-a)^2 = x^2 – 2ax + a^2\)
\((x-a)(x+a) = x^2 – a^2\)
左の状態から右の状態に式変形することを展開と言い、右の状態から左の状態に式変形することを因数分解と言います。おそらく中学数学ではこれを暗記させられると思います。
この記事では上の4つの公式を図形的に理解してみたいと思います。それではやっていきましょう。
1つ目の公式を理解する
1つ目の公式:
\((x+a)(x+b) = x^2 + (a+b)x + ab\)
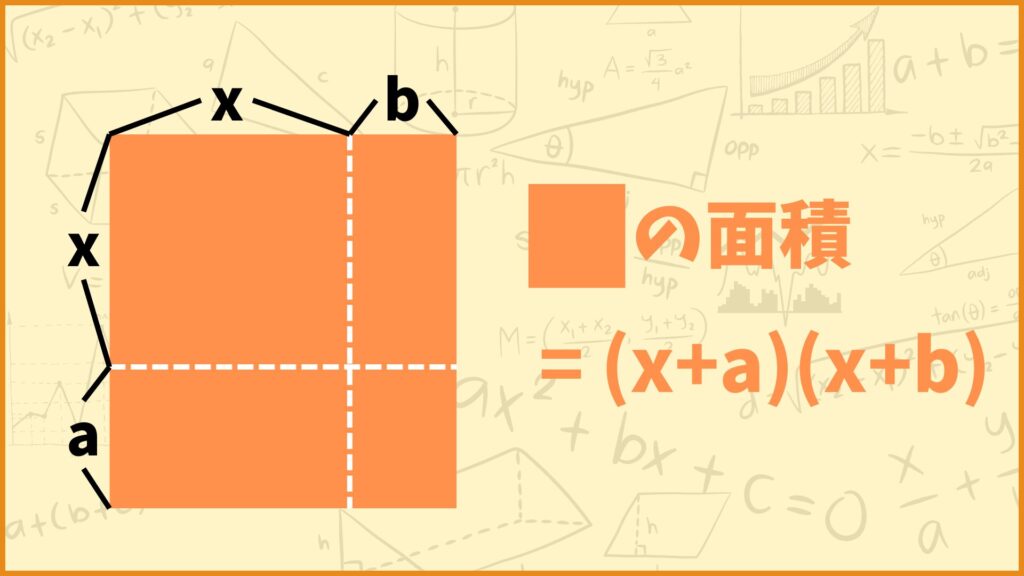
上図のようなオレンジの長方形を考えます。上の長方形は縦の長さが\((x+a)\)、横の長さが\((x+b)\)です。この図形の面積は
\((x+a)(x+b)\)
と表すことができます。それでは次に下図のように点線の白線で分けた4つの図形の面積について考えてみましょう。
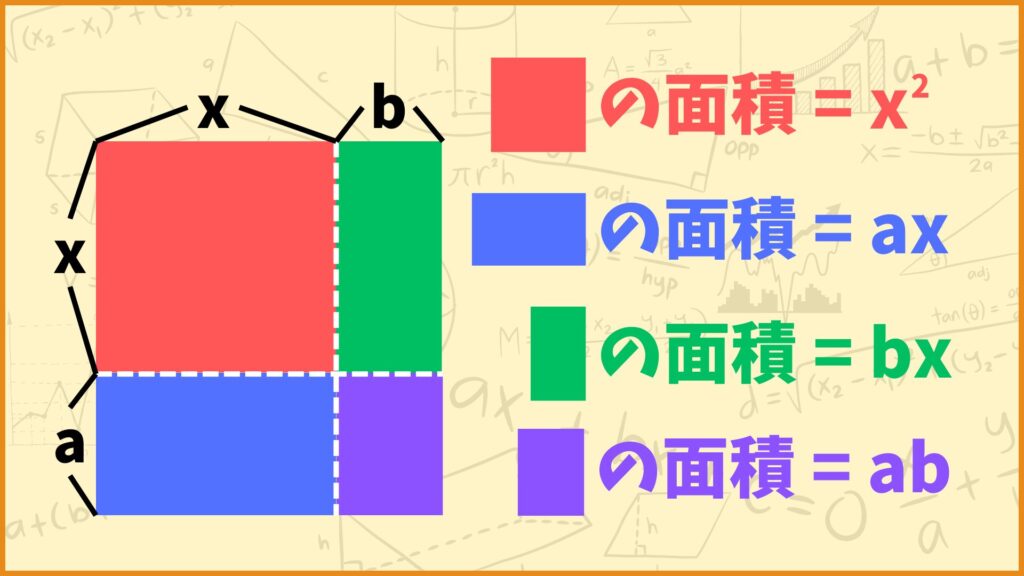
ということで赤、青、緑、紫の4つの図形に分けてみました。オレンジの図形の面積は赤、青、緑、紫の図形の面積を全部足した値と等しくなります。
まず赤い図形について考えてみましょう。赤い図形は縦の長さ、横の長さがともに\(x\)の正方形です。よって赤い図形の面積は
\(x \times x = x^2\)
となります。次に青い図形について考えてみましょう。青い図形は縦の長さが\(a\)、横の長さが\(x\)の長方形です。よって青い図形の面積は
\(a \times x = ax\)
となります。次に緑の図形について考えてみましょう。緑の図形は縦の長さが\(x\)、横の長さが\(b\)の長方形です。よって緑の図形の面積は
\(x \times b = bx\)
となります。最後に紫の図形について考えてみましょう。紫の図形は縦の長さが\(a\)、横の長さが\(b\)の長方形です。よって紫の図形の面積は
\(a \times b = ab\)
となります。これら4つの図形の面積を全部足してみましょう。
\(x^2 + ax + bx + ab = x^2 + (a+b)x + ab\)
これがオレンジの図形の面積\((x+a)(x+b)\)と同じになれば良いので、
\((x+a)(x+b) = x^2 + (a+b)x + ab\)
が成り立ちます。
1つ目の公式:
\((x+a)(x+b) = x^2 + (a+b)x + ab\)
2つ目の公式を理解する
2つ目の公式:
\((x+a)^2 = x^2 + 2ax + a^2\)
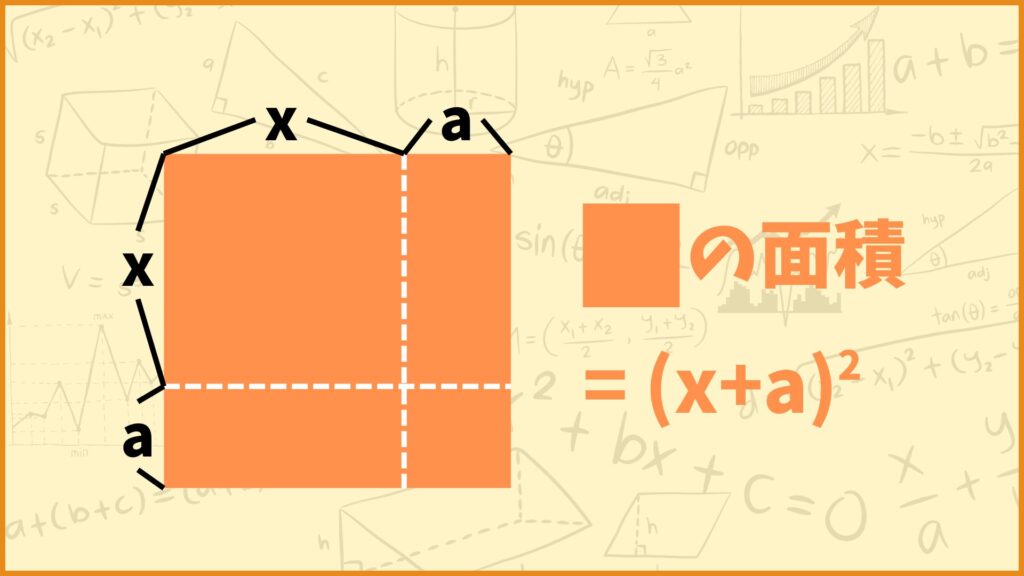
上図のような正方形を考えます。上の正方形は縦の長さ、横の長さがともに\((x+a)\)です。この図形の面積は
\((x+a)^2\)
と表すことができます。それでは次に点線の白線で分けた4つの図形の面積について考えてみましょう。
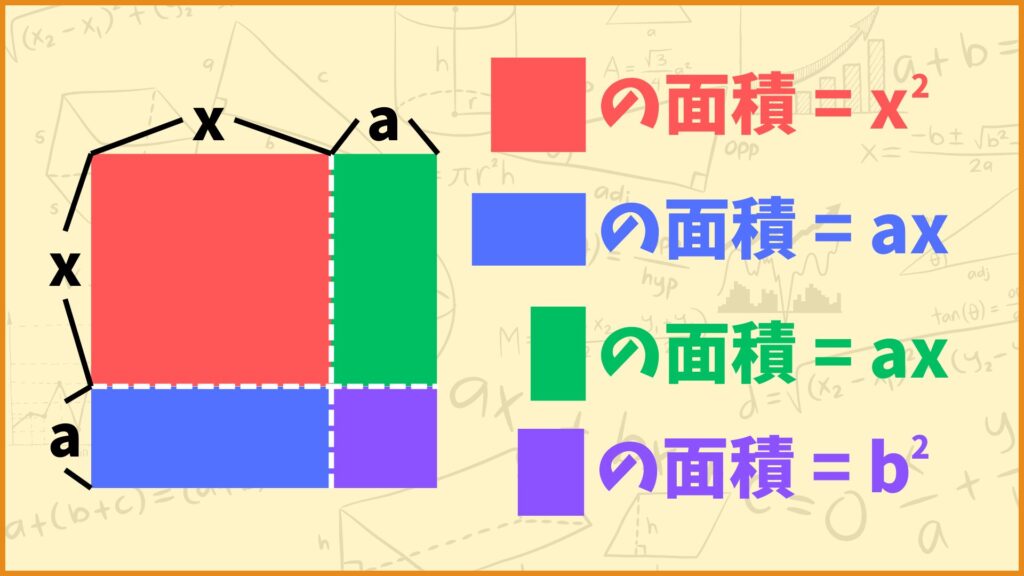
ということで赤、青、緑、紫の4つの図形に分けてみました。オレンジの図形の面積は赤、青、緑、紫の図形の面積を全部足した値と等しくなります。
まず赤い図形について考えてみましょう。赤い図形は縦の長さ、横の長さがともに\(x\)の正方形です。よって赤い図形の面積は
\(x \times x = x^2\)
となります。次に青い図形について考えてみましょう。青い図形は縦の長さが\(a\)、横の長さが\(x\)の長方形です。よって青い図形の面積は
\(a \times x = ax\)
となります。次に緑の図形について考えてみましょう。緑の図形は縦の長さが\(x\)、横の長さが\(a\)の長方形です。よって緑の図形の面積は
\(x \times a = ax\)
となります。最後に紫の図形について考えてみましょう。紫の図形は縦の長さ、横の長さがともに\(a\)の正方形です。よって紫の図形の面積は
\(a \times a = a^2\)
となります。これら4つの図形の面積を全部足してみましょう。
\(x^2 + ax + ax + a^2 = x^2 + 2ax + a^2\)
これがオレンジの図形の面積\((x+a)^2\)と同じになれば良いので、
\((x+a)^2 = x^2 + 2ax + a^2\)
が成り立ちます。
2つ目の公式:
\((x+a)^2 = x^2 + 2ax + a^2\)
3つ目の公式を理解する
3つ目の公式:
\((x-a)^2 = x^2 – 2ax + a^2\)
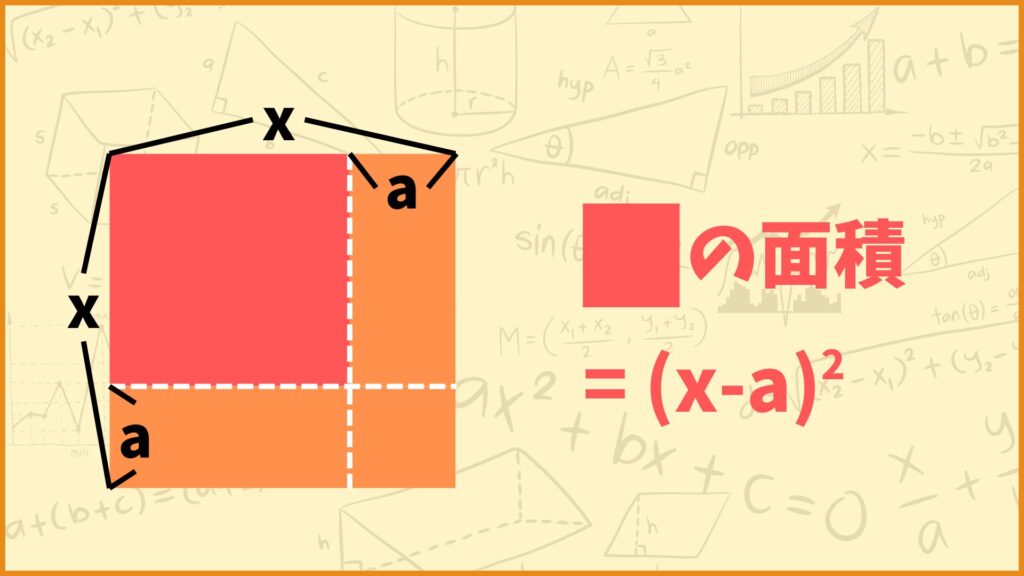
上図のような赤い正方形を考えます。上の赤い正方形は縦の長さ、横の長さがともに\((x-a)\)です。よって赤い正方形の面積は
\((x-a)^2\)
と表すことができます。次にこの赤い長方形を別の見方で考えてみましょう。
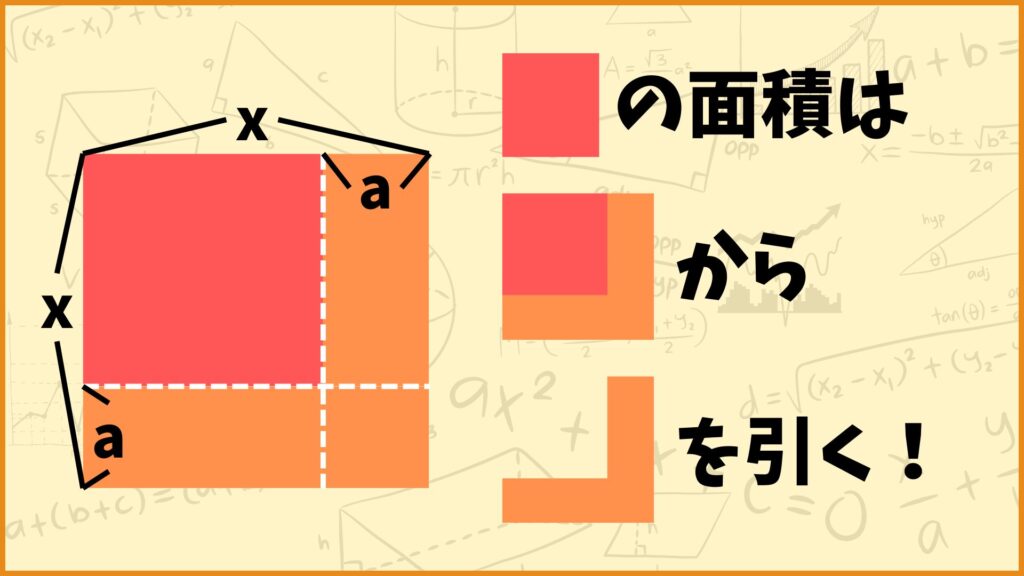
この赤い正方形の面積はでっかい正方形からL字の図形を引き算することで求めることができます。でっかい正方形は縦の長さ、横の長さがともに\(x\)なので面積は
\(x \times x = x^2\)
となります。次にL字の面積を考えてみましょう。L字の面積をそのまま計算するのは難しいので2つの長方形に分割して考えましょう。
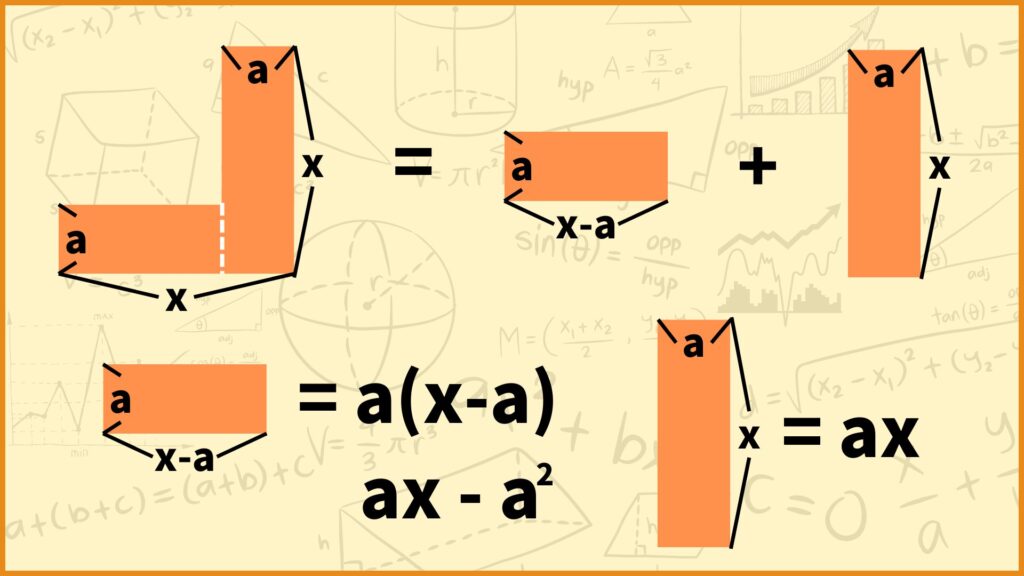
L字の図形を上のように2つの長方形に分割しました。1つ目の長方形は縦の長さが\(a\)、横の長さが\((x-a)\)なので面積は
\(a \times (x-a) = a(x-a) = ax – a^2\)
と計算できます。2つ目の長方形は縦の長さが\(x\)、横の長さが\(a\)なので面積は
\(x \times a= ax\)
と計算できます。よってでっかい正方形からこの2つの長方形を引き算すると
\(x^2 – (ax – a^2) – ax = x^2 – 2ax + a^2\)
これが赤い図形の面積\((x-a)^2\)と同じになれば良いので、
\((x-a)^2 = x^2 – 2ax + a^2\)
が成り立ちます。
3つ目の公式:
\((x-a)^2 = x^2 – 2ax + a^2\)
4つ目の公式を理解する
4つ目の公式:
\((x-a)(x+a) = x^2 – a^2\)
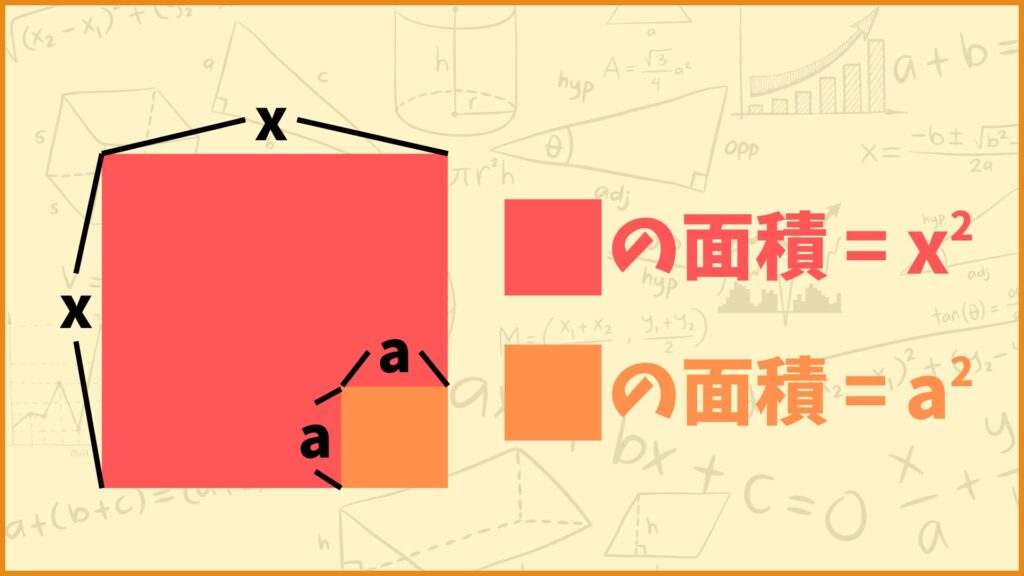
上図のような赤い正方形とオレンジの正方形を考えます。赤い正方形は縦の長さ、横の長さがともに\(x\)で、オレンジの正方形は縦の長さ、横の長さがともに\(a\)です。よってそれぞれの正方形の面積は
赤い正方形の面積:\(x^2\)
オレンジの正方形の面積:\(a^2\)
と表すことができます。よって赤い正方形からオレンジの正方形を除いた図形の面積は
\(x^2 – a^2\)
と表すことができます。次にこの赤い正方形からオレンジの正方形を除いた図形の面積を別の方法で求めてみましょう。
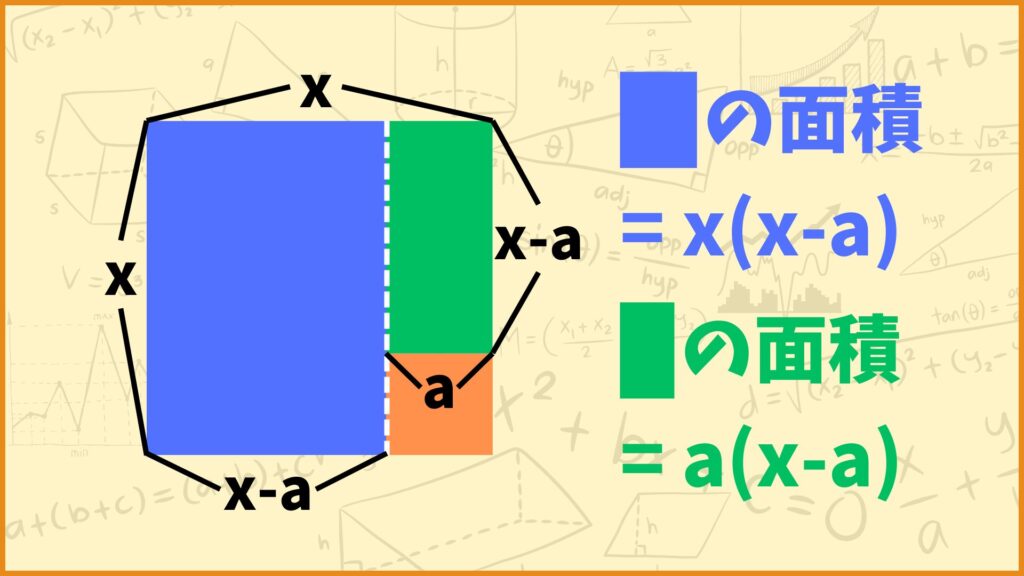
上図のように求めたい図形を青い長方形と緑の長方形の2つに分割します。この2つの長方形の面積をそれぞれ求めてみましょう。
青い長方形は縦の長さが\(x\)、横の長さが\(x-a\)なので面積は
\(x(x-a)\)
となります。緑の長方形は縦の長さが\(x-a\)、横の長さが\(a\)なので面積は
\(a(x-a)\)
となります。よって青い長方形と緑の長方形を合わせた図形の面積は
\(x(x-a) + a(x-a) = (x-a)(x+a)\)
と計算できます。
\(x(x-a)+a(x-a)\)は\((x-a)\)でくくることができるので上のように式変形できます。
となります。これが赤い正方形からオレンジの正方形を除いた図形の面積と等しくなるので
\((x-a)(x+a) = x^2 – a^2\)
が成立します。
4つ目の公式:
\((x-a)(x+a) = x^2 – a^2\)
おわりに
いかがでしたか。
今回の記事では展開・因数分解の公式について解説していきました。
最後までこの記事を読んでくれてありがとうございました。
普段は大学数学の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。



