こんにちは!しゅんです!
今回はラプラス行列について解説していきます!
ラプラス行列はグラフ理論で登場する数学用語です。ラプラス行列はグラフの全域木の数を数えるときに使える便利な行列なんです。
ということでこの記事ではラプラス行列がどんな行列なのか、そしてラプラス行列と接続行列の関係式について説明していきたいと思います。
それでは解説していきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
ラプラス行列ってなに?
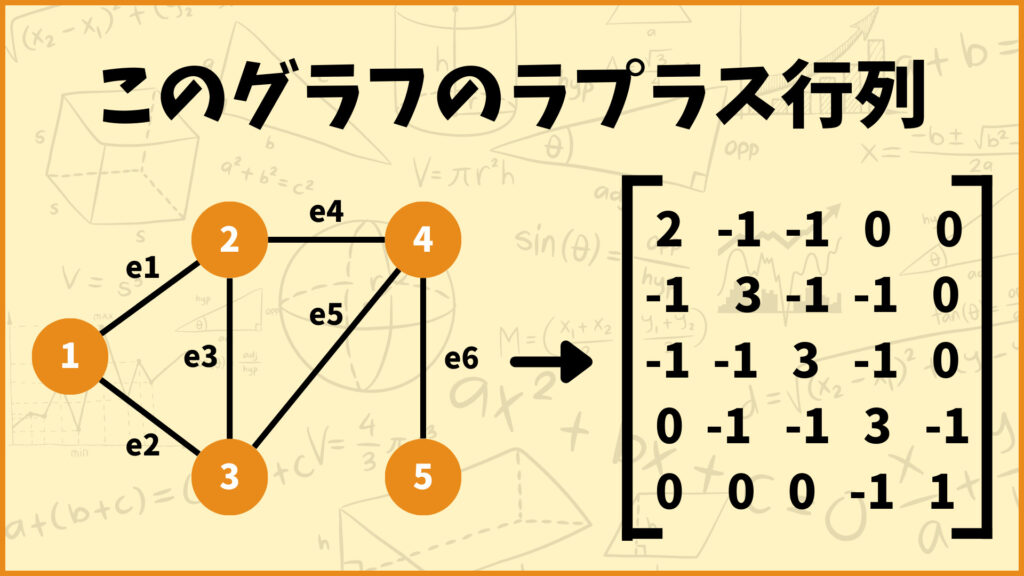
下のグラフを使ってラプラス行列を考えてみましょう。
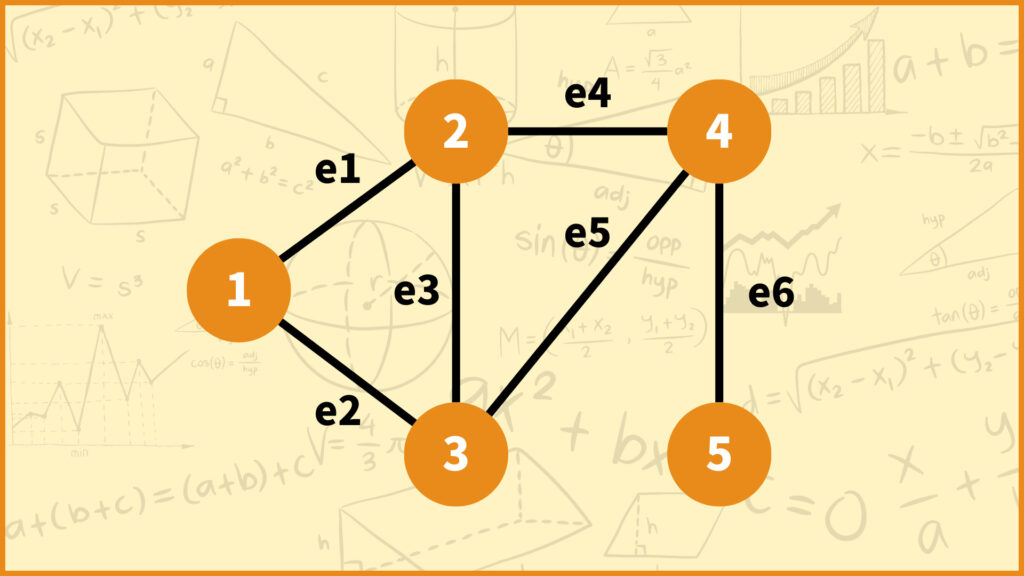
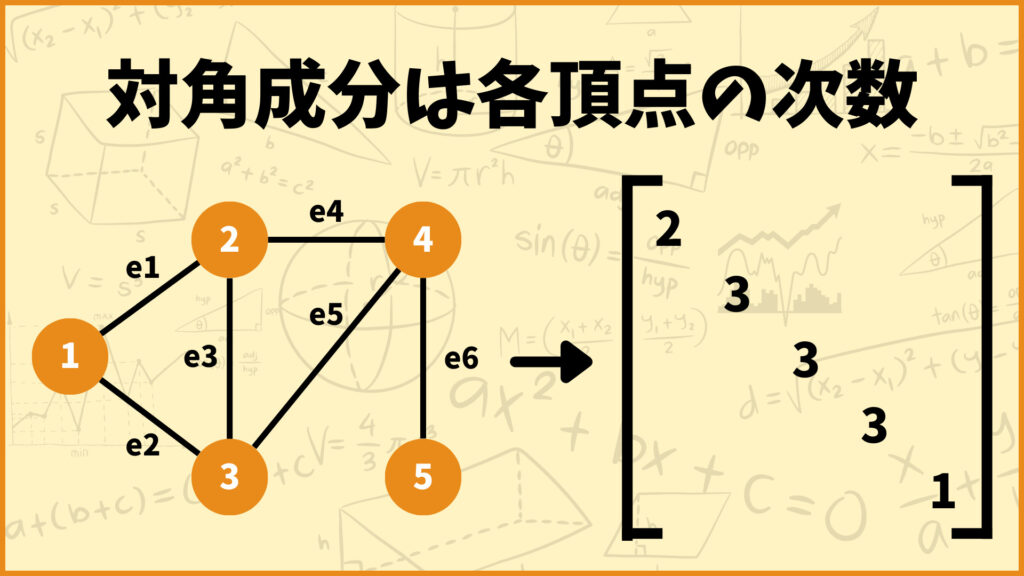
ラプラス行列の対角成分は各頂点の次数になります。次数とはその頂点に接続している辺の本数のことです。
例えば頂点1には辺\(e_1,\;e_2\)が接続しているので頂点1の次数は2となります。他にも例えば頂点3には辺\(e_2,\;e_3,e_5\)が接続しているので頂点3の次数は3となります。
頂点1 : 2
頂点2 : 3
頂点3 : 3
頂点4 : 3
頂点5 : 1
次に対角成分以外の\((i,j)\)成分は、辺\((i,j)\)が存在すれば-1、存在しなければ0となります。例えば\((1,2)\)成分は辺\((1,2) = e_1\)が存在するので-1となります。
また\((5,3)\)成分は辺\((5,3)\)が存在しないので0となります。以上のことをまとめるとこのグラフのラプラス行列は下図のようになります。
より厳密な定義は以下のようになります。
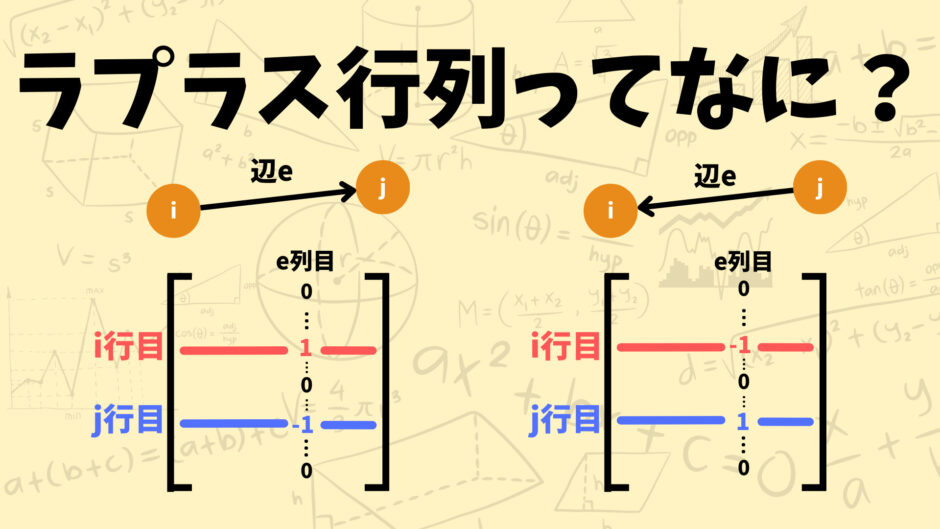
単純無向グラフ\(G=(V,E)\)に対して以下のように定義される正方行列\(L=(l_{ij})\in \mathbb{Z}\)を\(G\)のラプラス行列という。
\(l_{ij}=\left\{\begin{array}{l}\text{deg}(i) \;\;\; (i=j)\\ \;-1 \;\;\;\;\;\;\;\;\; (i\ne j \;\;\text{and} \;\;(i,j) \in E) \\ \;\;\;0 \;\;\;\;\;\;\;\;\;\;(\text{otherwise})\end{array}\right.\)
但し\(\text{deg}(i)\)は頂点\(i\)の次数。
接続行列ってなに?
無向グラフの場合
次に接続行列について考えたいと思います。こちらもさきほどのグラフを使って考えてみましょう。
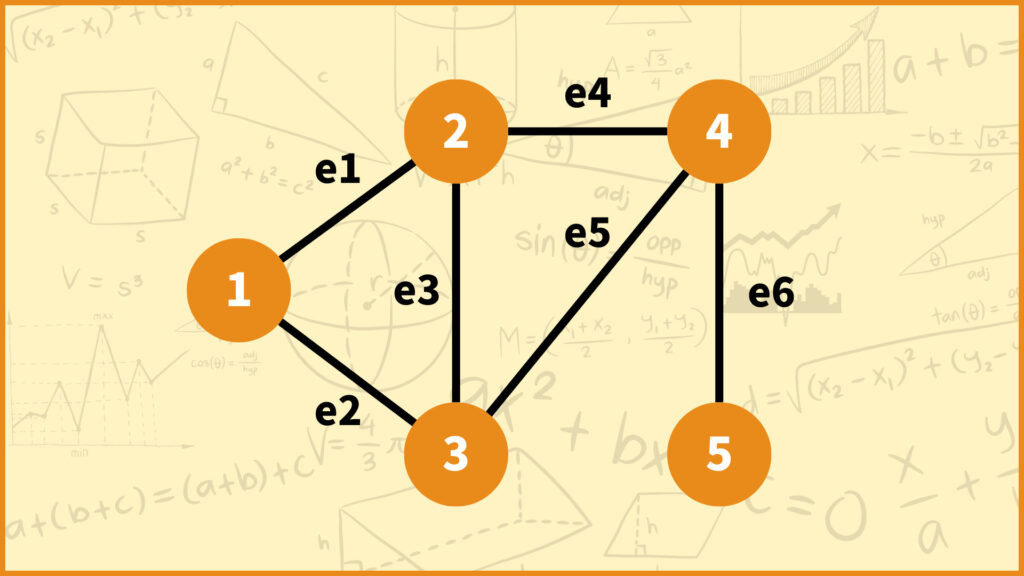
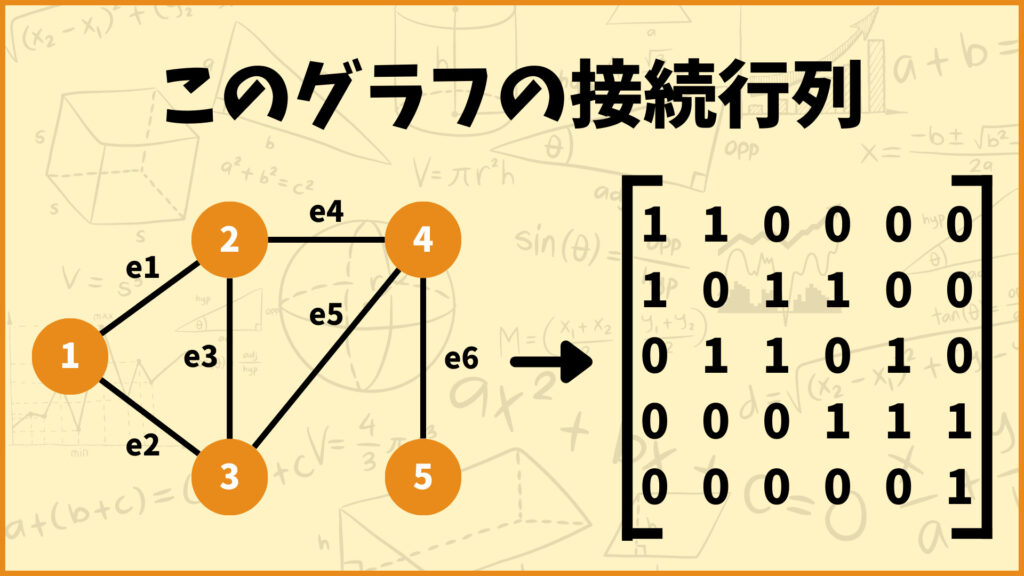
接続行列は各行が頂点、各列が辺を表しており、頂点に辺が接続していたら1、そうじゃなければ0をとります。例えば上のグラフを見てみると頂点2と辺\(e_3\)が接続しているので2行3列目の成分は1になります。
一方で頂点3と辺\(e_1\)は接続していません。そのため3行1列目の成分は0になります。このように考えていくと、このグラフの接続行列は下の図のようになります。
有向グラフの場合
接続行列は有向グラフの場合でも考えることができますが、無向グラフの場合と比べて少し面倒くさくなります。
無向グラフのときと同じように頂点と辺が接続しているかを考えるんですけど、有向グラフの場合は辺の向きがあるのでその頂点に向かう辺なのかその頂点から出ていく辺なのかを分けて考えます。
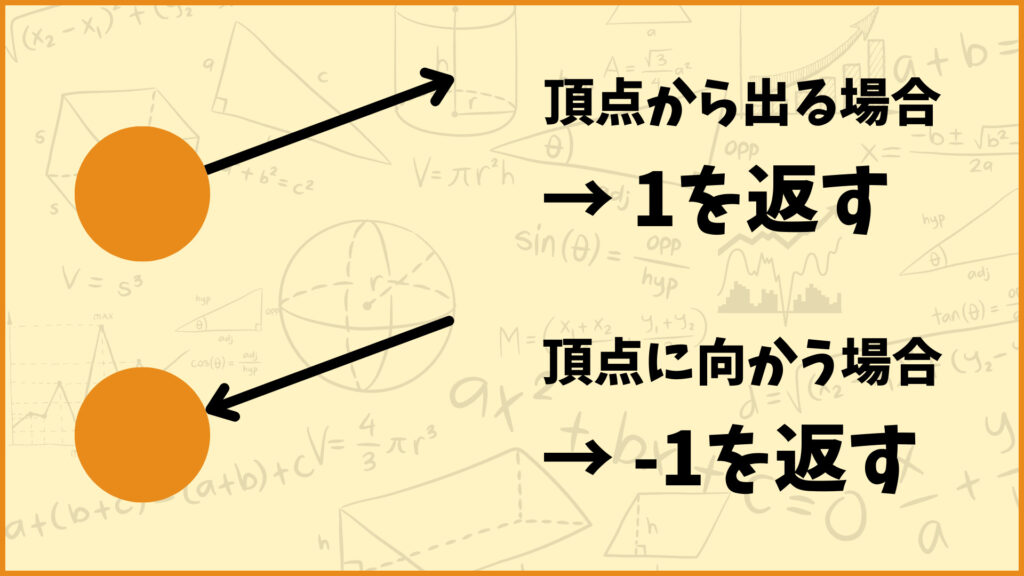
辺が頂点から出ていく場合は1、辺が頂点に向かう場合は-1を返します。例えば下の有向グラフの接続行列を考えてみましょう。
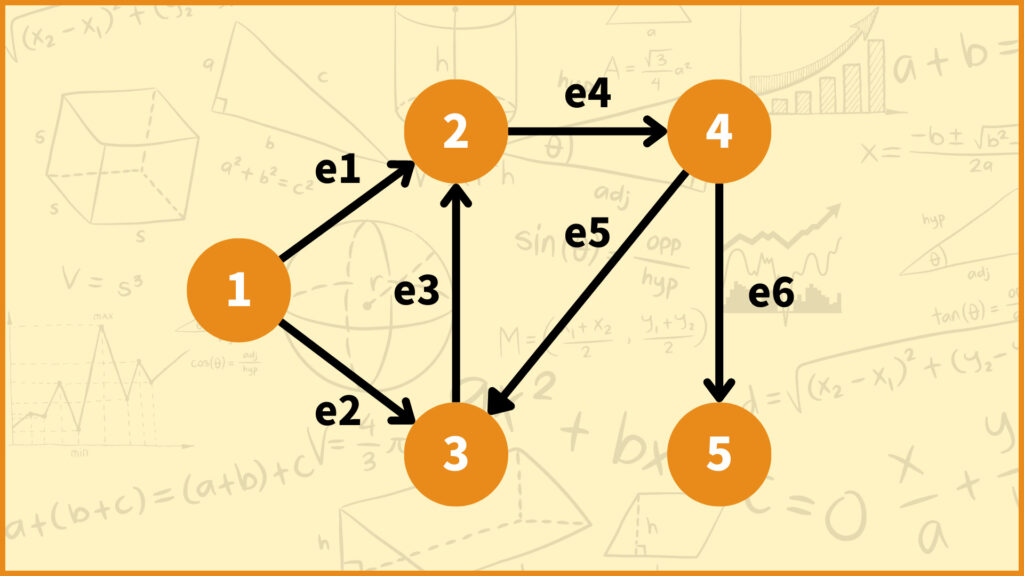
頂点1と辺\(e_1\)を見ると、辺\(e_1\)は頂点1から出ていく辺になっています。そのため1行1列目の成分は1となります。
頂点2と辺\(e_3\)を見ると、辺\(e_3\)は頂点2に向かう辺になっています。そのため2行3列目の成分は-1となります。
頂点4と辺\(e_2\)を見ると、そもそも接続していません。そのため4行2列目の成分は0となります。このように考えていくと、上のグラフの接続行列は下の図のようになります。
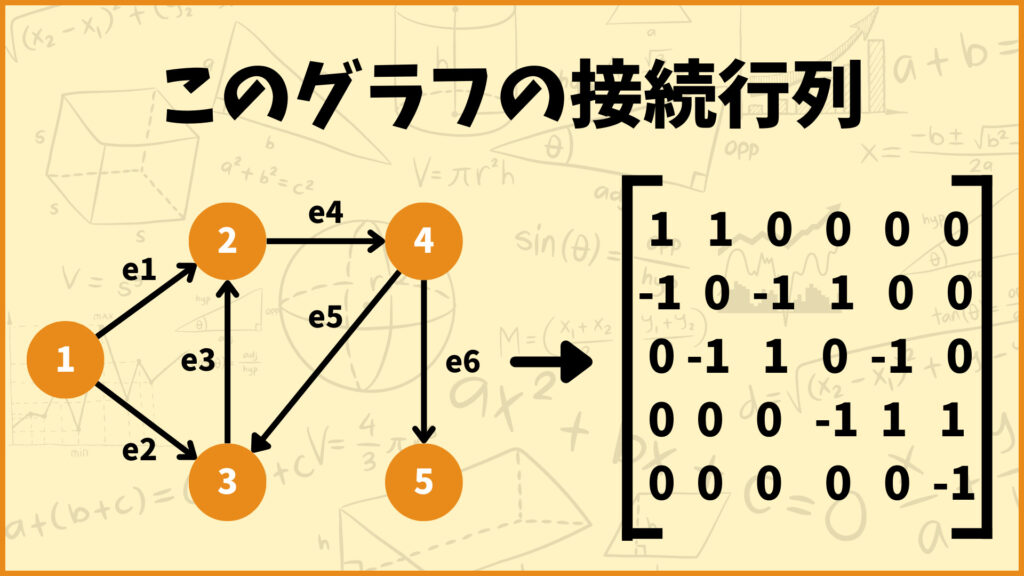
ラプラス行列と接続行列の関係
ラプラス行列と接続行列には非常に興味深い関係があります。ある無向グラフのラプラス行列を\(L\)、そのグラフを適当に向き付けしたグラフの接続行列を\(\overrightarrow{M}\)とすると以下の式が成立します。
\(L=\overrightarrow{M}\overrightarrow{M}^\top\)
先ほどのグラフを使って確かめてみましょう。
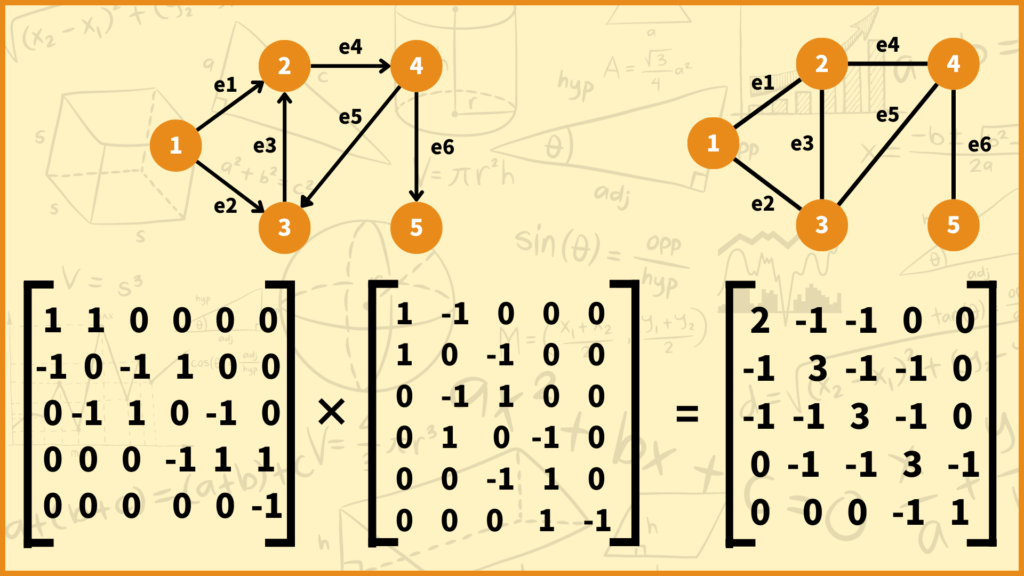
さきほど求めた有向グラフの接続行列とその転置の積を計算すると、たしかに無向グラフのラプラス行列となっていますね。
今回は上図のような向き付けをしましたが、別にどんな向き付けにしても必ず成り立ちます。
ラプラス行列と接続行列の関係を証明する
それでは最後になぜこんなことが成り立つのかを証明していきたいと思います。行列の知識を使うので少し難しいかもしれませんが、なるべく分かりやすく解説したいと思います!
証明の流れ
証明したいのは以下の式です。
\(L=\overrightarrow{M}\overrightarrow{M}^\top\)
この式を証明するために、\(\overrightarrow{M}\overrightarrow{M}^\top\)のすべての\((i,j)\)成分の値がラプラス行列\(L\)の\((i,j)\)成分と一致することを示します。
つまり第二章で説明したラプラス行列の定義式と一致することを示します。\(\overrightarrow{M}\overrightarrow{M}^\top\)の\((i,j)\)成分を\((\overrightarrow{M}\overrightarrow{M}^\top)_{ij}\)と表すと証明したい式は以下のようになります。
\((\overrightarrow{M}\overrightarrow{M}^\top)_{ij}=\left\{\begin{array}{l}\text{deg}(i) \;\;\; (i=j)\\ \;-1 \;\;\;\;\;\;\;\;\; (i\ne j \;\;\text{and} \;\;(i,j) \in E) \\ \;\;\;0 \;\;\;\;\;\;\;\;\;\;(\text{otherwise})\end{array}\right.\)
但し\(\text{deg}(v_i)\)は頂点\(v_i\)の次数。
1. 事前準備
証明をするためにいくつか文字を設定します。\(\overrightarrow{M}\)の\((i,j)\)成分を\(\overrightarrow{M}_{ij}\)、\(\overrightarrow{M}^\top\)の\((i,j)\)成分を\((\overrightarrow{M}^\top)_{ij}\)とします。
2. \(\overrightarrow{M}\overrightarrow{M}^\top\)の\((i,j)\)成分を考える
\(\overrightarrow{M}\overrightarrow{M}^\top\)の\((i,j)\)成分を求めるためには、\(\overrightarrow{M}\)の\(i\)行目と\(\overrightarrow{M}^\top\)の\(j\)列目を使います。
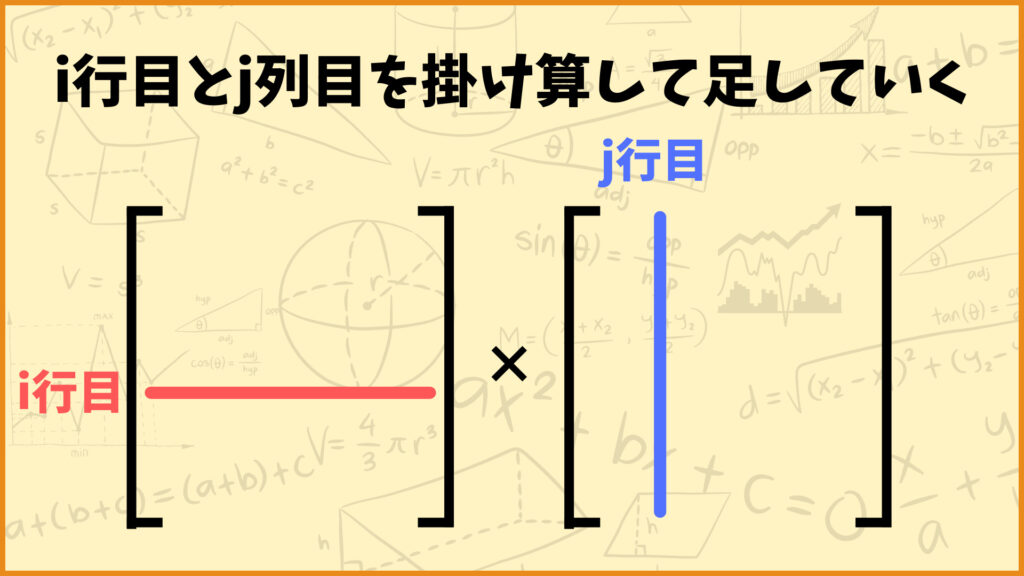
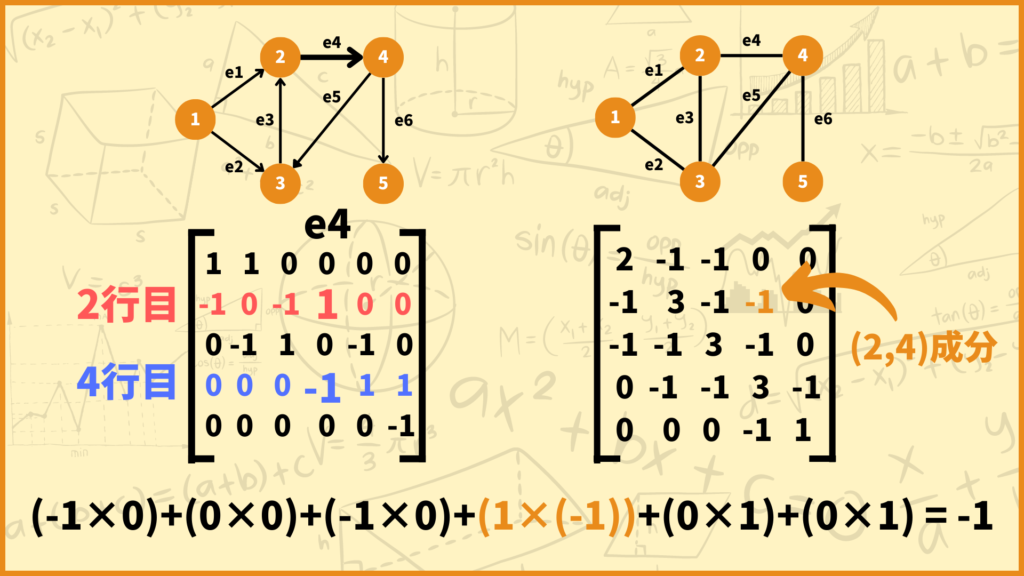
ここでポイントとなるのが、積を求めている行列が\(\overrightarrow{M}\)と\(\overrightarrow{M}^\top\)であるということです。転置の性質から\(\overrightarrow{M}^\top\)の\(j\)列目は\(\overrightarrow{M}\)の\(j\)行目と等しいので、\(\overrightarrow{M}\overrightarrow{M}^\top\)の\((i,j)\)成分は\(\overrightarrow{M}\)の\(i\)行目と\(j\)行目をかけて足していけば求めることができます。
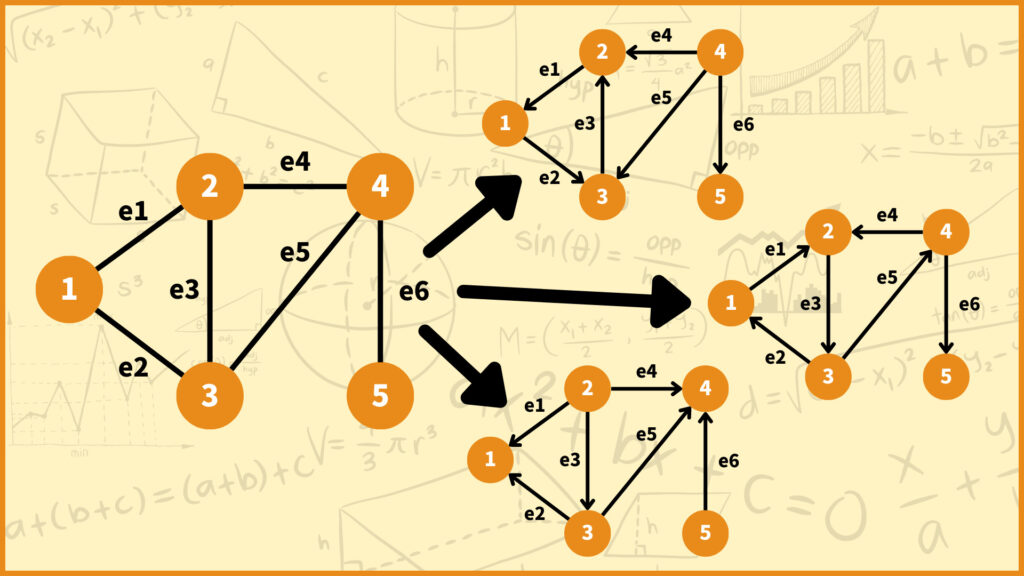
さっきのグラフを使って考えてみます。例えばあのグラフのラプラス行列の\((2,4)\)成分は-1でしたが、接続行列の2行目と4行目をかけて足し算したらちゃんと-1になっています。
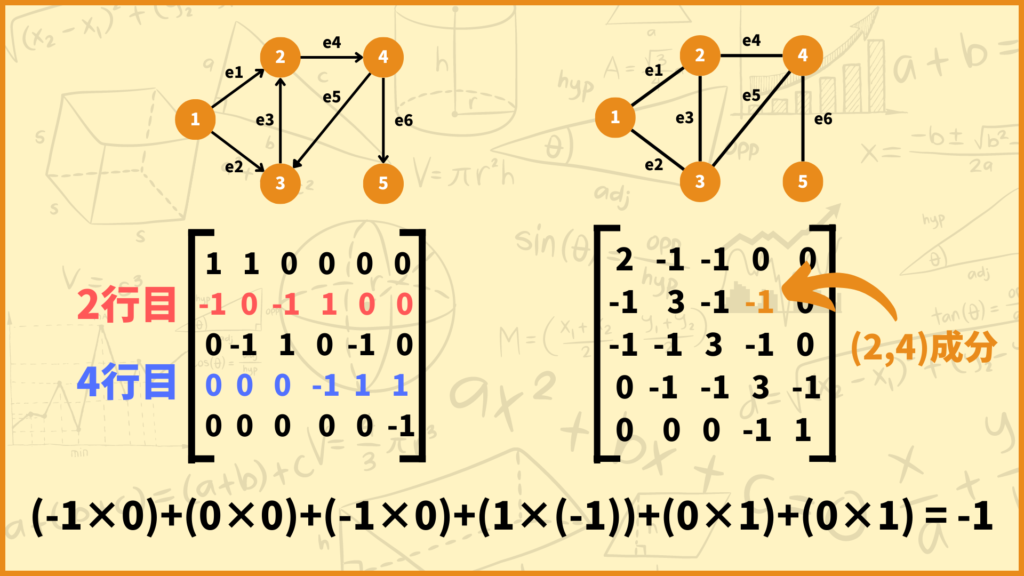
このことを式で表すと以下のようになります。
\((\overrightarrow{M}\overrightarrow{M}^\top)_{ij}\)
\(=\sum\limits^d_{e=1}\overrightarrow{M}_{ie}(\overrightarrow{M}^\top)_{ej}\)
\(=\sum\limits^d_{e=1}\overrightarrow{M}_{ie}\overrightarrow{M}_{je}\)
但し\(d\)は辺の数
3. 3パターンに場合分けする
次に下のように3パターンに場合分けをします。
1. \(i=j\)のとき
2. \(i \ne j\)かつ\((i,j) \in E\)のとき
3. それ以外
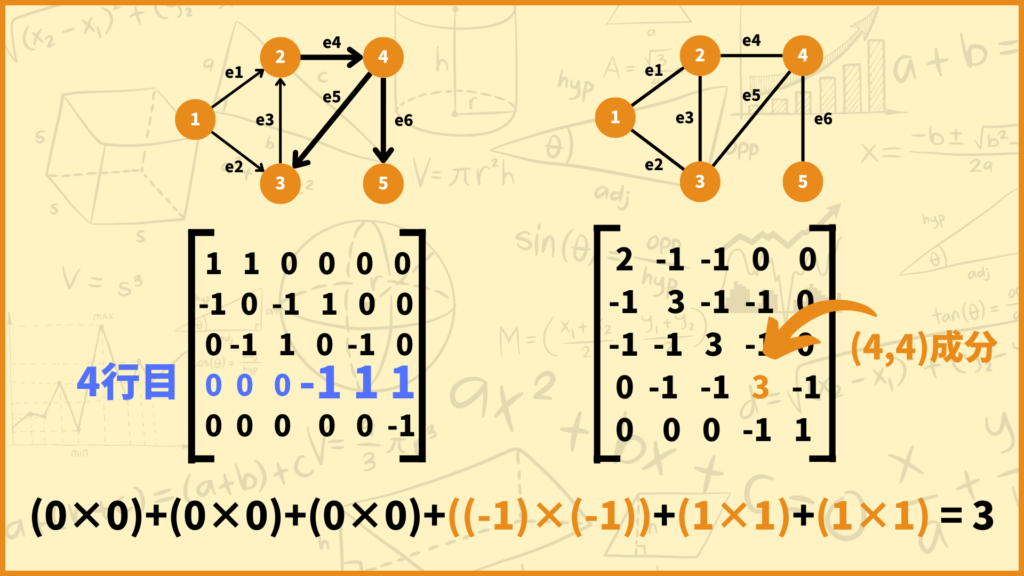
まず\(i=j\)のときは\(\overrightarrow{M}_{ie}\)と\(\overrightarrow{M}_{je}\)は同じ値になります。さっきのグラフを使うと以下のようになります。
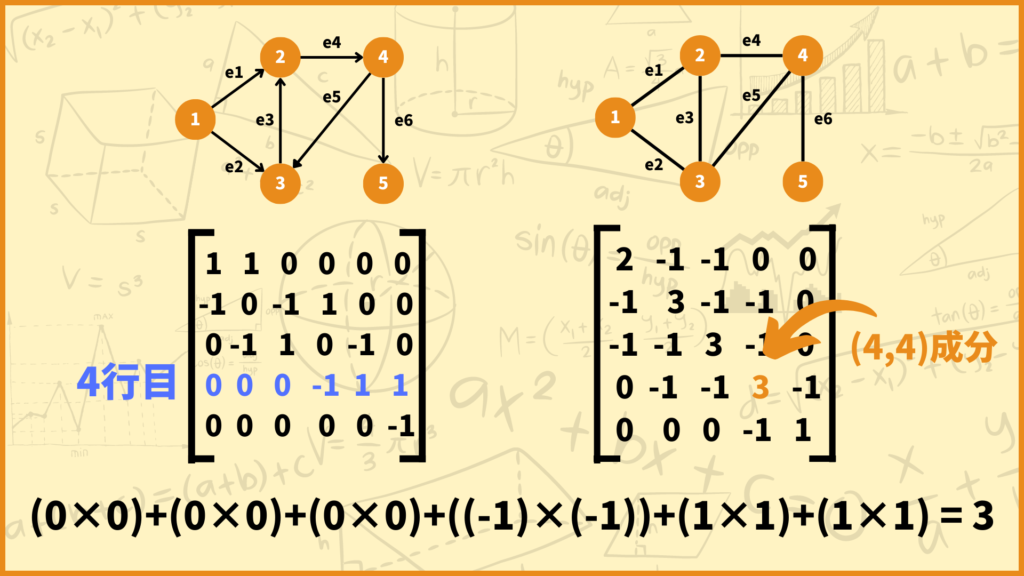
\(i=j=4\)の場合を考えてみましょう。\((4,4)\)成分を計算したいときは、4行目と4行目の数字をかけて足していきます。式で表すと下のようになります。
\(\sum\limits^d_{e=1}\overrightarrow{M}_{ie}\overrightarrow{M}_{je}=\sum\limits^d_{e=1}(\overrightarrow{M}_{ie})^2\) (\(i=j\)のとき)
次に\(i \ne j\)かつ\((i,j) \in E\)のときを考えてみましょう。
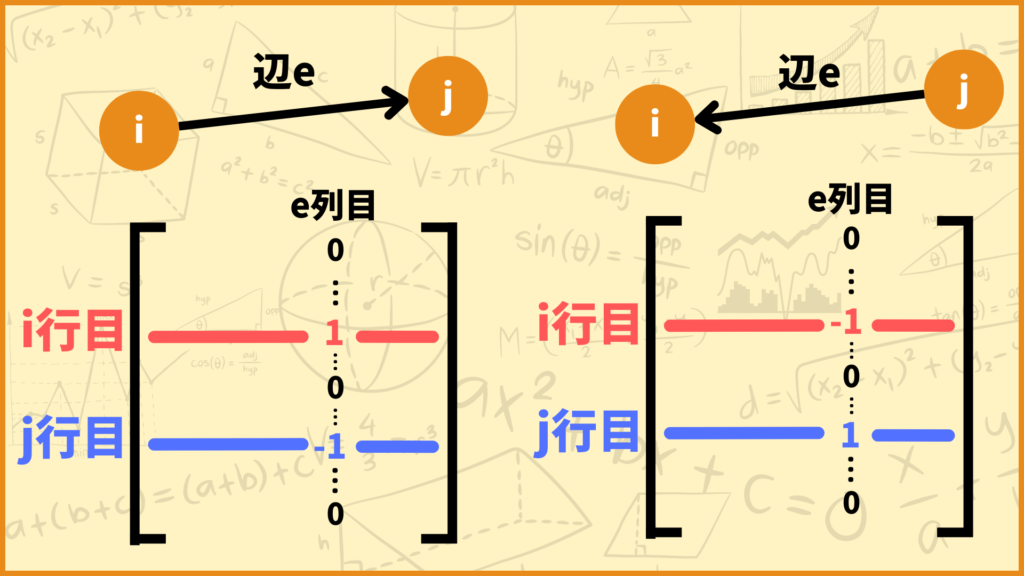
頂点\(i\)と頂点\(j\)の間に辺\(e\)があるとします。接続行列を作るときには辺\(e\)に向きを付ける必要があります。
頂点\(i\)から頂点\(j\)に向かって辺\(e\)が伸びていると仮定しましょう。このとき接続行列の\((i,e)\)成分の値が1になり、\((j,e)\)成分の値が-1になります。
またほかの列は\(i\)行目か\(j\)行目のどちらかの値が必ず0になります。すなわち\(\sum\limits^d_{e=1}\overrightarrow{M}_{ie}\overrightarrow{M}_{je}\)の値が-1になります。
もし両方とも0じゃなかったら単純グラフであることに矛盾してしまいますね。
頂点\(j\)から頂点\(i\)に向かって辺\(e\)が伸びている場合は、接続行列の\((i,e)\)成分が-1、\((j,e)\)成分が1となりますね。
いずれの場合でも\(\sum\limits^d_{e=1}\overrightarrow{M}_{ie}\overrightarrow{M}_{je}\)の値が-1になることが分かります。
さっきのグラフを使うと以下のようになります。
最後にそれ以外の場合を考えてみましょう。つまり\(i \ne j\)かつ\((i,j)\notin E\)の場合を考えます。このときは先ほど考えていたように、接続行列の\(i\)と\(j\)行目の値のどちらかが必ず0になります。
どちらも0でなかったら\((i,j)\notin E\)に矛盾しますね。
ということで\(\sum\limits^d_{e=1}\overrightarrow{M}_{ie}\overrightarrow{M}_{je}\)の値が0になります。
以上のことをまとめると下のようになります。
\((\overrightarrow{M}\overrightarrow{M}^\top)_{ij}=\left\{\begin{array}{l}\sum\limits^d_{e=1}(\overrightarrow{M}_{ie})^2 \;\;\; (i=j)\\ \;-1 \;\;\;\;\;\;\;\;\; (i\ne j \;\;\text{and} \;\;(i,j) \in E) \\ \;\;\;0 \;\;\;\;\;\;\;\;\;\;(\text{otherwise})\end{array}\right.\)
4. \(\sum\limits^d_{e=1}(\overrightarrow{M}_{ie})^2=\text{deg}(i)\)を示す
\(\sum\limits^d_{e=1}(\overrightarrow{M}_{ie})^2\)について考えてみましょう。例えば下の図の頂点\(i\)について\(\sum\limits^d_{e=1}(\overrightarrow{M}_{ie})^2\)を計算すると4になります。
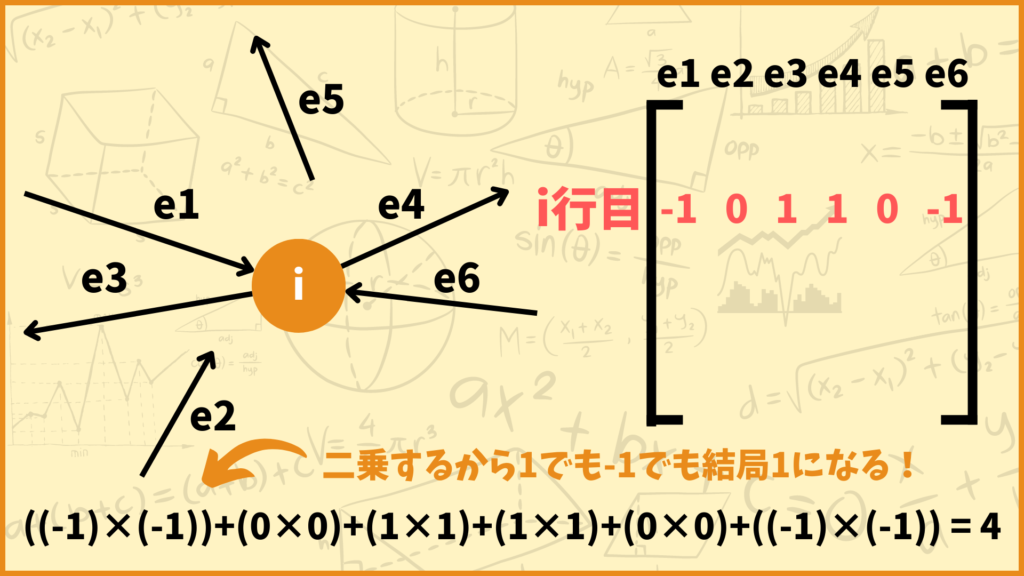
ある辺\(e\)が頂点\(i\)に接続していると\(\overrightarrow{M}_{ie}\)の値は1か-1になります。そのため\((\overrightarrow{M}_{ie})^2\)の値は1になります。(上図で言うと辺\(e_1,\;e_3,\;e_4,\;e_6\))
逆に辺\(e\)が頂点\(i\)に接続していないと\(\overrightarrow{M}_{ie}\)の値は0になるので\((\overrightarrow{M}_{ie})^2\)の値は0になります。(上図で言うと辺\(e_2,\;e_5\))
つまりすべての辺\(e\)に対して\((\overrightarrow{M}_{ie})^2\)を足し算していくと、頂点\(i\)に接続している辺の数だけ大きくなります。上の図でいうと頂点\(i\)に4本の辺が接続しているので\(\sum\limits^d_{e=1}(\overrightarrow{M}_{ie})^2=4\)となります。
例えばさっきのグラフだと下図のようになります。
頂点\(i\)に接続している辺の本数を次数と呼び、\(\text{deg}(i)\)と表します。
以上より\(\sum\limits^d_{e=1}(\overrightarrow{M}_{ie})^2=\text{deg}(i)\)が成り立ちます。ということで以下の式が成り立つのでラプラス行列と接続行列の関係式を証明することができました。
\((\overrightarrow{M}\overrightarrow{M}^\top)_{ij}=\left\{\begin{array}{l}\text{deg}(i) \;\;\; (i=j)\\ \;-1 \;\;\;\;\;\;\;\;\; (i\ne j \;\;\text{and} \;\;(i,j) \in E) \\ \;\;\;0 \;\;\;\;\;\;\;\;\;\;(\text{otherwise})\end{array}\right.\)
但し\(\text{deg}(v_i)\)は頂点\(v_i\)の次数。
おわりに
いかがでしたか。
今回の記事ではラプラス行列について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。