こんにちは!しゅんです!
今回はマージソートについて解説していきます!
データを分析するときに小さい順に数字を並べる操作は頻繁に行います。そんなときに使うのがマージソートという手法です。
この記事ではマージソートというアルゴリズムについて、基本的な考え方や実装方法を分かりやすく解説していきます。
また今回はpythonを使って実際にマージソートを実装していきたいと思います。
それでは解説していきましょう!
普段はNBAのデータ分析をしたりしています。
ぜひこちらの記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
マージソートの基本的な考え方
マージソートの基本的な考え方は「大きな問題は分割して考える」です。この考え方を基にして2つのステップを実行することで並べ替えができます。
それでは1つずつ解説していきましょう。
説明では以下の例を使って考えてみます。下の数字列を小さい順に並べることを考えます。
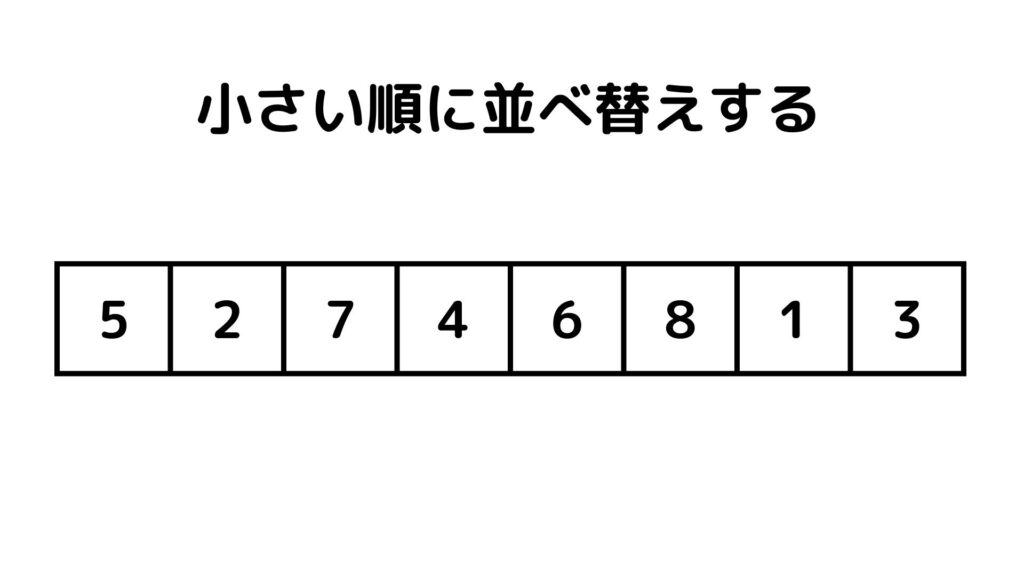
STEP. 1 分割
STEP. 1は分割です。上の数字列をそのまま並べ替えするのは大変なので、2つの数字列に分割するところからマージソートは始まります。
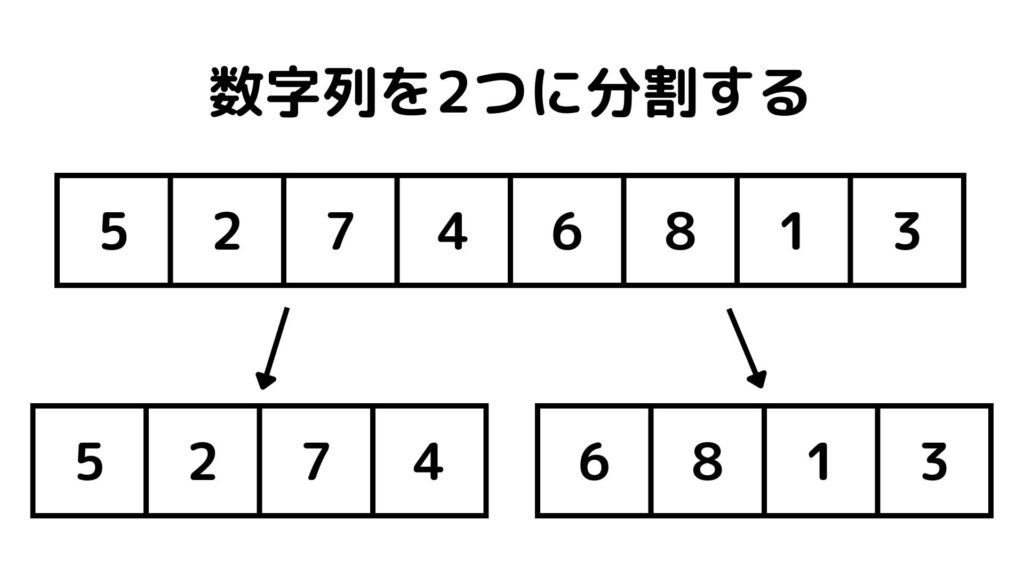
分割することで8個の数字を並べ替える問題が4個の数字を並べ替える問題に変わりました。
マージソートではさらにこれらの数字列を分割して、最終的に1個しか数字がない列を8個作ります。(数字が1つだと数字列とは呼べないかもしれませんが…)
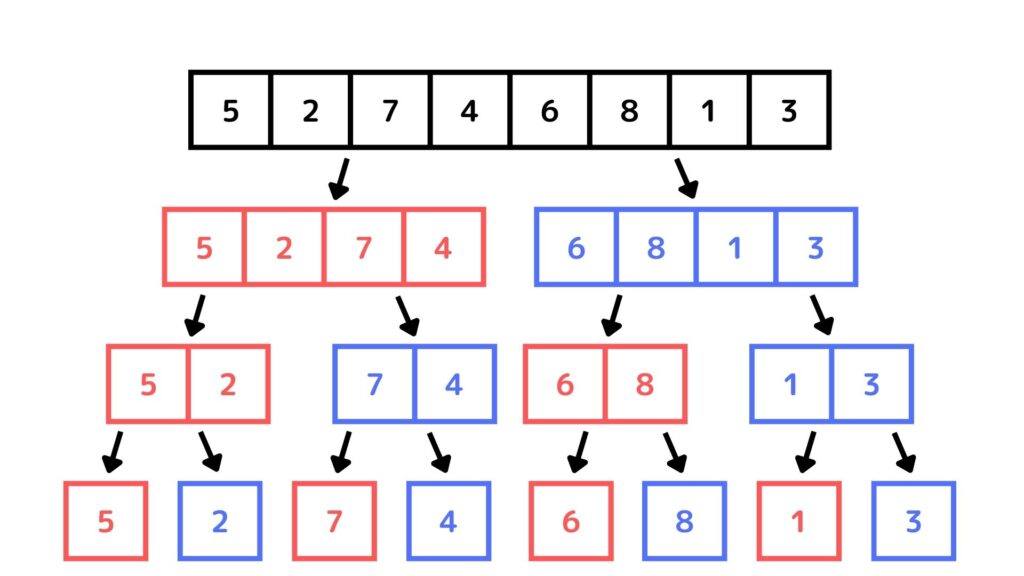
ということでSTEP. 1の分割が完了しました。ここからは次のステップである統合について解説します。
STEP. 2 統合
ここからは分割した数字列をまた統合していきます。この際統合の仕方に以下の工夫が必要なので注意しましょう。
統合するときには必ず数字が小さい順になるようにしましょう。
例えば5と2を統合する際には2,5の順番になるように統合します。一見当たり前のように見えますね。
なぜ数字が1つになるまで分割して統合するのかという疑問が出てくるかもしれませんが、このようにすることで後々非常に楽になります。

この操作をさっきの分割とは逆方向に行っていくわけです。次に要素数が2個の数字列同士を統合して4個の数字列を作る場合を考えてみましょう。
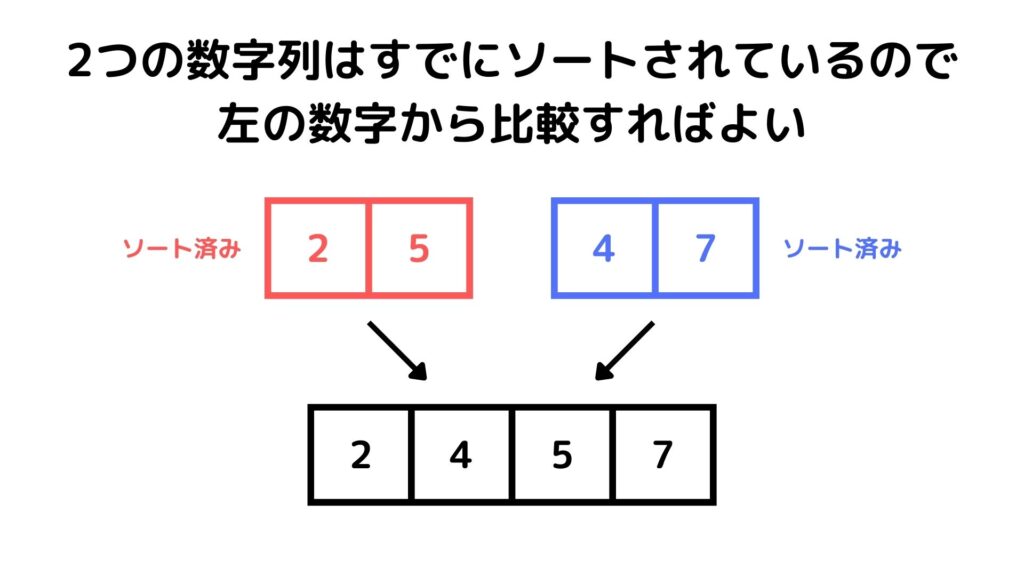
このときも数字が小さい順になるように統合するんですが、統合する2つの数字列は既に小さい順に統合されているはずです。
つまり各列の左から順番に比較すれば良いのです。これが文字列を要素数が1つになるまで分割する理由です。
すでにソートされている数字列同士を統合するのか、それともランダムな順番の数字列同士を統合するのかでは計算量が大きく変わります。
マージソートの魅力は普通に並べるのに比べて計算量が少なくなるという点にあります。
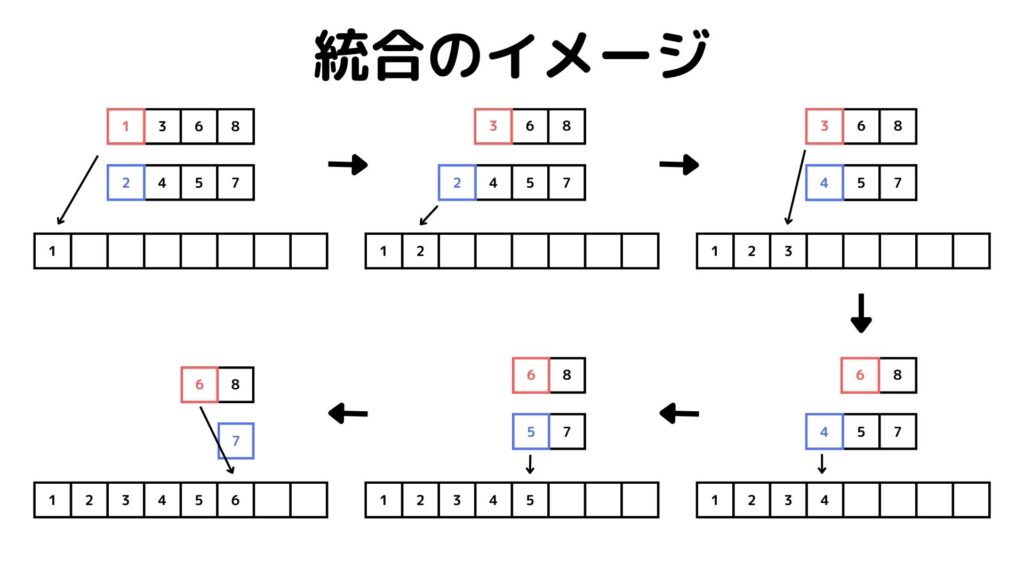
上の図のように左から順に赤と青の数字を比較して統合することで、計算量を少なくソートできます。
それでは次にpythonを使ってマージソートを実装してみましょう。
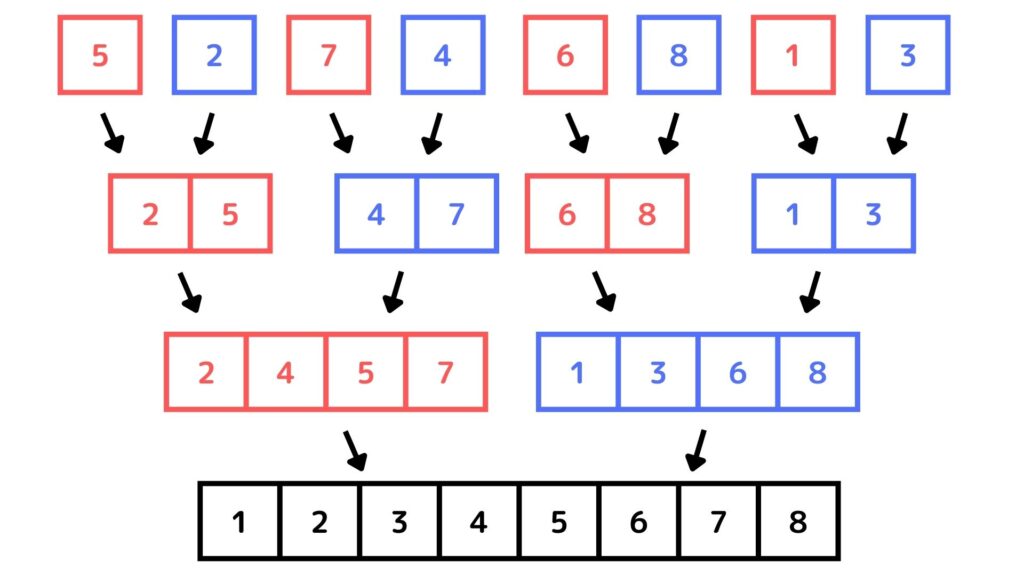
マージソートのようにそのままでは解決しづらい問題を分割して、それぞれで最適解を見つけてそれを統合することによって全体の最適解を見つける方法を分割統治法(divide-and-conquer method)と言います。
pythonでマージソートを実装する
コードは以下のようになります。
def Merge_Sort(A):
if len(A) <= 1: # リストの長さが1以下ならそのまま返す(ソートする必要がないため)
return A
mid = len(A)//2 # リストの真ん中の番号を取得
# リストをLeftとRightに分割する
Left = A[:mid]
Right = A[mid:]
Left_Sort = Merge_Sort(Left) # Leftというリストに対して再びMerge_Sort(分割)を実行する
Right_Sort = Merge_Sort(Right) # Rightというリストに対して再びMerge_Sort(分割)を実行する
Sorted_A = Merge(Left_Sort, Right_Sort) # Left_SortとRight_Sortを統合する(この下でMergeは定義してます)
return(Sorted_A) # ソートしたリストを返す
def Merge(Left, Right):
result = []
i = j = 0
while i < len(Left) and j < len(Right): # LeftとRightのどちらかの数字をすべて追加するまで以下の操作を行う
# Leftのi番目の数字がRightのj番目の数字より大きい場合にLeftのi番目の数字をresultに追加する
if Left[i] <= Right[j]:
result.append(Left[i])
i += 1
# そうじゃない場合はRightのj番目の数字をresultに追加する
else:
result.append(Right[j])
j += 1
result += Left[i:] # resultにLeftの残りを追加する
result += Right[j:] # resultにRightの残りを追加する
return result # resultを返す試しに実行してみましょう。
test = [3,2,1,4,5]
Merge_Sort(test)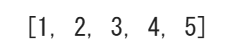
ということで小さい順に並び替えることができましたね。まずはMerge_Sort関数から説明していこうと思います。
Merge_Sort関数の説明
def Merge_Sort(A):
if len(A) <= 1: # リストの長さが1以下ならそのまま返す(ソートする必要がないため)
return A
mid = len(A)//2 # リストの真ん中の番号を取得
# リストをLeftとRightに分割する
Left = A[:mid]
Right = A[mid:]
Left_Sort = Merge_Sort(Left) # Leftというリストに対して再びMerge_Sort(分割)を実行する
Right_Sort = Merge_Sort(Right) # Rightというリストに対して再びMerge_Sort(分割)を実行する
Sorted_A = Merge(Left_Sort, Right_Sort) # Left_SortとRight_Sortを統合する(この下でMergeは定義してます)
return(Sorted_A) # ソートしたリストを返すMerge_Sort関数は1次元のリストAが入力されたときに中身を小さい順に並べ替えて返す関数です。
2~3行目は入力されたリストAに要素数が1個以下の場合の操作を表しています。
if len(A) <= 1: # リストの長さが1以下ならそのまま返す(ソートする必要がないため)
return A要素数がが0個、1個のときは並べ替える必要が無いのでそのままAを返します。
4行目からはリストの分割操作を行っています。リストのちょうど真ん中をmidと名付けて、それより左の要素をLeft、右の要素をRightとします。
mid = len(A)//2 # リストの真ん中の番号を取得
# リストをLeftとRightに分割する
Left = A[:mid]
Right = A[mid:]8, 9行目ではLeft、Rightそれぞれに対して再びMerge_Sort関数を適用しています。つまりLeft、Rightをさらに分割していくわけです。最終的にリストの要素数が1になるまで分割しますが、そうなると2~3行目の条件に一致するためそのまま返すわけです。
このように1つの関数の中に同じ関数を呼び出すことを再帰呼び出しと言います。
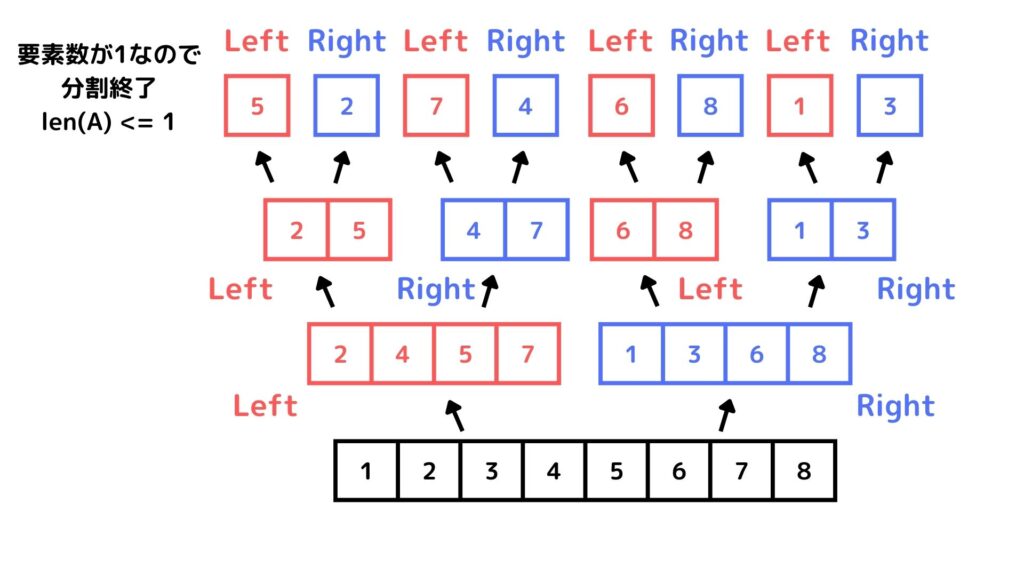
11行目ではこの後解説するMerge関数を使ってLeft_SortとRight_Sortを統合します。このときに小さい順に並べるわけです。
Sorted_A = Merge(Left_Sort, Right_Sort) # Left_SortとRight_Sortを統合する(この下でMergeは定義してます)そして12行目で並べ替えたリストAを返しています。
Merge関数の説明
def Merge(Left, Right):
result = []
i = j = 0
while i < len(Left) and j < len(Right): # LeftとRightのどちらかの数字をすべて追加するまで以下の操作を行う
# Leftのi番目の数字がRightのj番目の数字より大きい場合にLeftのi番目の数字をresultに追加する
if Left[i] <= Right[j]:
result.append(Left[i])
i += 1
# そうじゃない場合はRightのj番目の数字をresultに追加する
else:
result.append(Right[j])
j += 1
result += Left[i:] # resultにLeftの残りを追加する
result += Right[j:] # resultにRightの残りを追加する
return result # resultを返すMerge関数はLeft、Rightの2つのリストが入力されたときに、数字が小さい順になるように統合して返す関数です。
2行目では空のリストを作っています。この後この空リストに数字を追加します。
result = []3行目から12行目では2つのリストを左から順に比べていって、数字が小さい方をresultに追加しています。
i = j = 0
while i < len(Left) and j < len(Right): # LeftとRightのどちらかの数字をすべて追加するまで以下の操作を行う
# Leftのi番目の数字がRightのj番目の数字より大きい場合にLeftのi番目の数字をresultに追加する
if Left[i] <= Right[j]:
result.append(Left[i])
i += 1
# そうじゃない場合はRightのj番目の数字をresultに追加する
else:
result.append(Right[j])
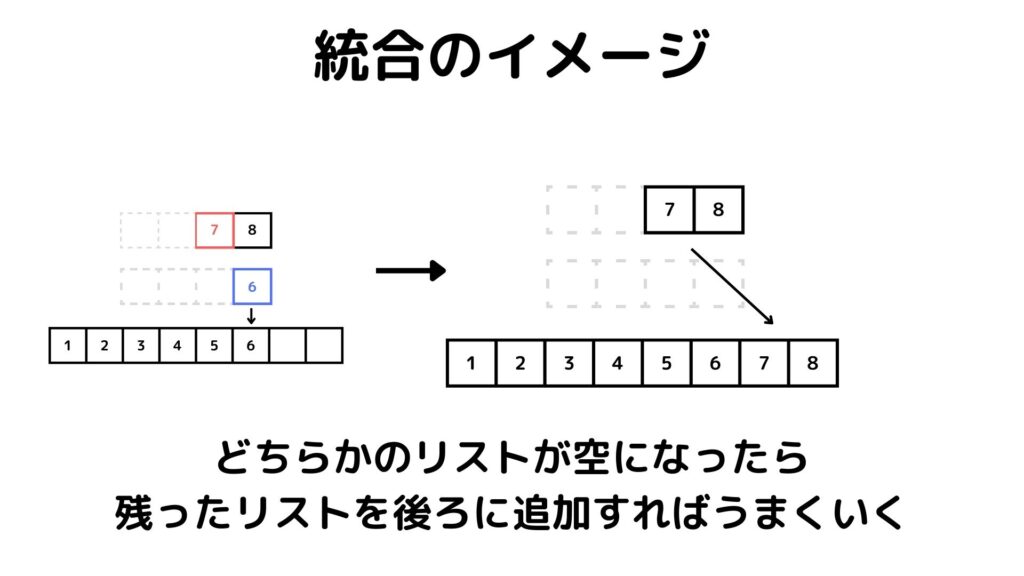
j += 113, 14行目はリストに残っている数字をすべて追加します。というのも、統合するリストは既にソートされているので、どちらかのリストの要素が空になった時点で残りのリストの要素をそのまま追加していけば上手くいくのです。
どちらかは必ず空リストになるので下のコードのどちらかは要素を追加しない意味ない行になっています。
result += Left[i:] # resultにLeftの残りを追加する
result += Right[j:] # resultにRightの残りを追加する下の図のようなイメージです。
最後の行でresultを返しています。
return result # resultを返すpythonでマージソートを実行する
ランダムで50個の数字を生み出してそれをマージソートで小さい順に並べてみました。
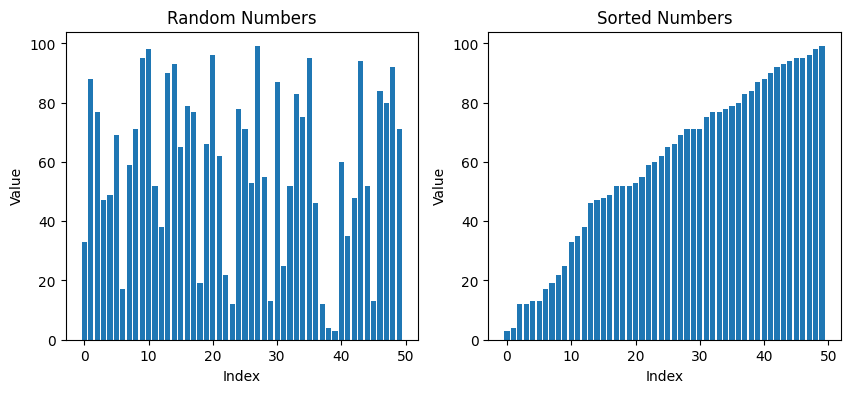
左図がランダムに生成された50この数字で、右図がそれをマージソートを使用した結果です。
ちゃんと小さい順に並べられていますね。
おわりに
いかがでしたでしょうか。
今回の記事ではpythonを使ってマージソートについて解説していきました
こんな感じでプログラミングを使えばいろいろなことができます。非常に興味深いですよね。
これからもこのようにプログラミングで色々やっていきたいと思います。ぼくが一番勉強になるので続けていきたいです!
最後までこの記事を読んでくれてありがとうございました。



