こんにちは!しゅんです!
今回の記事ではマージソートとバブルソートでどれくらい計算時間が変わるのかを、pythonを使って調べていきたいと思います。

この記事ではアルゴリズムの説明やpythonのコードの説明はせず、計算時間に着目していきます。
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
マージソートをpythonで実装する
def Merge_Sort(A):
if len(A) <= 1: # リストの長さが1以下ならそのまま返す(ソートする必要がないため)
return A
mid = len(A)//2 # リストの真ん中の番号を取得
# リストをLeftとRightに分割する
Left = A[:mid]
Right = A[mid:]
Left_Sort = Merge_Sort(Left) # Leftというリストに対して再びMerge_Sort(分割)を実行する
Right_Sort = Merge_Sort(Right) # Rightというリストに対して再びMerge_Sort(分割)を実行する
Sorted_A = Merge(Left_Sort, Right_Sort) # Left_SortとRight_Sortを統合する(この下でMergeは定義してます)
return(Sorted_A) # ソートしたリストを返す
def Merge(Left, Right):
result = []
i = j = 0
while i < len(Left) and j < len(Right): # LeftとRightのどちらかの数字をすべて追加するまで以下の操作を行う
# Leftのi番目の数字がRightのj番目の数字より大きい場合にLeftのi番目の数字をresultに追加する
if Left[i] <= Right[j]:
result.append(Left[i])
i += 1
# そうじゃない場合はRighMtのj番目の数字をresultに追加する
else:
result.append(Right[j])
j += 1
result += Left[i:] # resultにLeftの残りを追加する
result += Right[j:] # resultにRightの残りを追加する
return result # resultを返す
上のコードがpythonでマージソートを実行するためのコードです。簡単に説明します。
まずこのコードでは2つの関数を定義しています。1つ目の関数がMerge_Sort()で2つ目の関数がMerge()です。引数はそれぞれリストAと2つのリストleft,rightです。
Merge_Sort()関数ではリストAを入力すると、Aをどんどん分割して最終的に分割したリストの要素数が1になるまで分割します。そしたら2つ目の関数であるMerge()関数を使って分割したリストをどんどんくっつけていきます。
Merge()関数は2つのリストLeftとRightが与えられたらそれを1つのリストにくっつける関数です。このときに各リストの左側から要素を見ていき、小さい方を先に追加するという操作を繰り返しています。
詳しい話はこちらの記事で解説しています!
バブルソートをpythonで実装する
def Bubble_Sort(A):
n = len(A)
for i in range(n):
for j in range(0, n-i-1):
if A[j] > A[j+1]:
A[j], A[j+1] = A[j+1], A[j]
return A
上のコードがpythonでバブルソートを実行するためのコードです。簡単に説明します。
このコードではBubble_Sort()という関数を定義しています。引数はリストAです。

例えば[5,7,4,8,6,3,2,1]のリストをソートすることを考えます。今「i=0」とします。「for j in range(0, n-i-1)」は「for j in range(0,n-1)」となり、j=0,1,2,3,4,5,6について考えます。
「if A[j] > A[j+1]:」でA[j]とA[j+1]の大小関係を調べています。j=0のときA[0]=5,A[1]=7となり、A[j]>A[j+1]となりません。そのためリストには何も変化を加えません。
j=1のときA[1]=7,A[2]=4となり、A[j]>A[j+1]となります。そのため「A[j], A[j+1] = A[j+1], A[j]」で7と4の順番を入れ替えます。
このような操作を繰り返していくことでリストを小さい順にソートするのがバブルソートです。
詳しい話はこちらの記事で解説しています!
現在制作中
計算時間がどれくらい変わるかを調べる
それではpythonを使ってマージソートとバブルソートでどれくらい計算時間が変わるかを調べてみます。
## 事前準備
import time
import random
import matplotlib.pyplot as plt
##関数の定義
# マージソート
def Merge_Sort(A):
if len(A) <= 1: # リストの長さが1以下ならそのまま返す(ソートする必要がないため)
return A
mid = len(A)//2 # リストの真ん中の番号を取得
# リストをLeftとRightに分割する
Left = A[:mid]
Right = A[mid:]
Left_Sort = Merge_Sort(Left) # Leftというリストに対して再びMerge_Sort(分割)を実行する
Right_Sort = Merge_Sort(Right) # Rightというリストに対して再びMerge_Sort(分割)を実行する
Sorted_A = Merge(Left_Sort, Right_Sort) # Left_SortとRight_Sortを統合する(この下でMergeは定義してます)
return(Sorted_A) # ソートしたリストを返す
def Merge(Left, Right):
result = []
i = j = 0
while i < len(Left) and j < len(Right): # LeftとRightのどちらかの数字をすべて追加するまで以下の操作を行う
# Leftのi番目の数字がRightのj番目の数字より大きい場合にLeftのi番目の数字をresultに追加する
if Left[i] <= Right[j]:
result.append(Left[i])
i += 1
# そうじゃない場合はRightのj番目の数字をresultに追加する
else:
result.append(Right[j])
j += 1
result += Left[i:] # resultにLeftの残りを追加する
result += Right[j:] # resultにRightの残りを追加する
return result # resultを返す
# バブルソート
def Bubble_Sort(A):
n = len(A)
for i in range(n):
for j in range(0, n-i-1):
if A[j] > A[j+1]:
A[j], A[j+1] = A[j+1], A[j]
return A
## マージソートとバブルソートの計算時間を比較する
time_list_merge = []
time_list_bubble = []
N_list = [i for i in range(100,5001,100)] # 要素数100から5000まで100刻み
for N in N_list:
for i in range(10): # 各Nに対して10回ソートする
t_m = []
t_b = []
A = [random.randint(0,100) for _ in range(N)] # ソートするリストを用意する
# マージソートの計算時間を記録する
start_time_m = time.time()
Merge_Sort(A)
end_time_m = time.time()
t_m.append(end_time_m-start_time_m)
# バブルソートの計算時間を記録する
start_time_b = time.time()
Bubble_Sort(A)
end_time_b = time.time()
t_b.append(end_time_b-start_time_b)
#10回の平均値を求めてtime_listに追加する
avg_time_m = sum(t_m)/len(t_m)
time_list_merge.append(avg_time_m)
avg_time_b = sum(t_b)/len(t_b)
time_list_bubble.append(avg_time_b)
## 結果のグラフを表示する
plt.figure(figsize = (10,6))
plt.plot(N_list,time_list_merge, marker = "o", color = "blue", label = "Merge Sort")
plt.plot(N_list,time_list_bubble, marker = "o", color = "red", label = "Bubble Sort")
plt.xlabel("length of list")
plt.ylabel("time (s)")
plt.legend()
plt.show()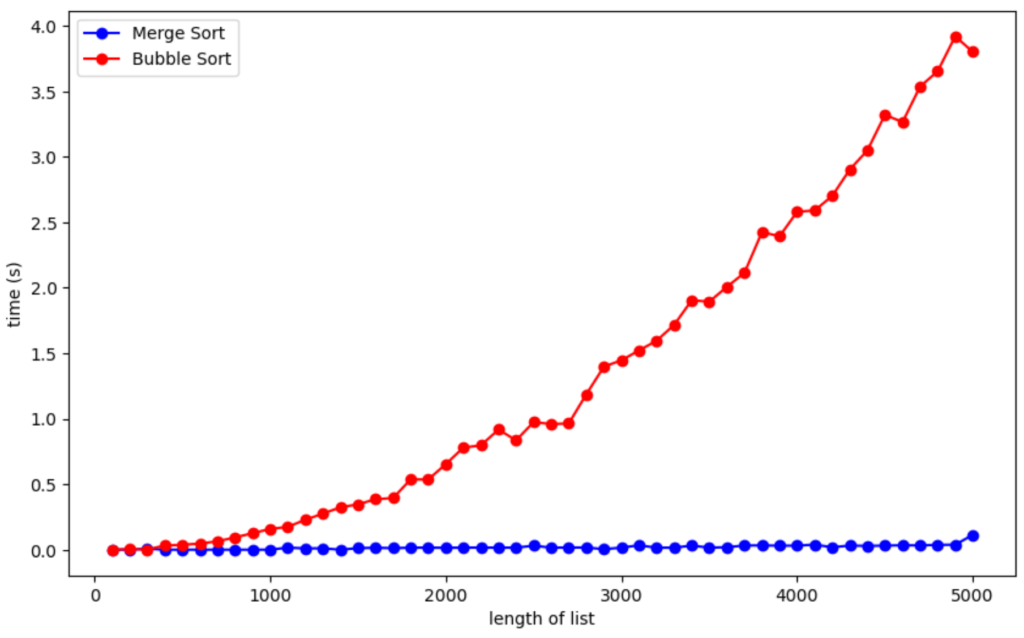
このコードを実行したら上のグラフが表示されました。それではコードについて1つずつ説明していきます。
事前準備
## 事前準備
import time
import random
import matplotlib.pyplot as plt
計算時間を調べるための事前準備としてtime,random,matplotlibモジュールをインポートしています。
timeは時間を測るために使います。
randomはランダムな数字列を生成するために使います。
matplotlibはグラフを描画するために使います。
関数の定義
##関数の定義
# マージソート
def Merge_Sort(A):
if len(A) <= 1: # リストの長さが1以下ならそのまま返す(ソートする必要がないため)
return A
mid = len(A)//2 # リストの真ん中の番号を取得
# リストをLeftとRightに分割する
Left = A[:mid]
Right = A[mid:]
Left_Sort = Merge_Sort(Left) # Leftというリストに対して再びMerge_Sort(分割)を実行する
Right_Sort = Merge_Sort(Right) # Rightというリストに対して再びMerge_Sort(分割)を実行する
Sorted_A = Merge(Left_Sort, Right_Sort) # Left_SortとRight_Sortを統合する(この下でMergeは定義してます)
return(Sorted_A) # ソートしたリストを返す
def Merge(Left, Right):
result = []
i = j = 0
while i < len(Left) and j < len(Right): # LeftとRightのどちらかの数字をすべて追加するまで以下の操作を行う
# Leftのi番目の数字がRightのj番目の数字より大きい場合にLeftのi番目の数字をresultに追加する
if Left[i] <= Right[j]:
result.append(Left[i])
i += 1
# そうじゃない場合はRightのj番目の数字をresultに追加する
else:
result.append(Right[j])
j += 1
result += Left[i:] # resultにLeftの残りを追加する
result += Right[j:] # resultにRightの残りを追加する
return result # resultを返す
# バブルソート
def Bubble_Sort(A):
n = len(A)
for i in range(n):
for j in range(0, n-i-1):
if A[j] > A[j+1]:
A[j], A[j+1] = A[j+1], A[j]
return A
ここではマージソートとバブルソートを関数で定義しています。ここの説明は飛ばします。
マージソートとバブルソートの計算時間を比較する
## マージソートとバブルソートの計算時間を比較する
time_list_merge = []
time_list_bubble = []
N_list = [i for i in range(100,5001,100)] # 要素数100から5000まで100刻み
for N in N_list:
for i in range(10): # 各Nに対して10回ソートする
t_m = []
t_b = []
A = [random.randint(0,100) for _ in range(N)] # ソートするリストを用意する
# マージソートの計算時間を記録する
start_time_m = time.time()
Merge_Sort(A)
end_time_m = time.time()
t_m.append(end_time_m-start_time_m)
# バブルソートの計算時間を記録する
start_time_b = time.time()
Bubble_Sort(A)
end_time_b = time.time()
t_b.append(end_time_b-start_time_b)
#10回の平均値を求めてtime_listに追加する
avg_time_m = sum(t_m)/len(t_m)
time_list_merge.append(avg_time_m)
avg_time_b = sum(t_b)/len(t_b)
time_list_bubble.append(avg_time_b)
ここではマージソートとバブルソートの計算時間を比較しています。この部分は少し詳しく説明したいと思います。
2~4行目
time_list_merge = []
time_list_bubble = []
N_list = [i for i in range(100,5001,100)] # 要素数100から5000まで100刻み
2行目ではマージソートの計算時間のデータを取っておくための初期リストを定義しています。
3行目ではバブルソートの計算時間のデータを取っておくための初期リストを定義しています。
4行目では数字列の長さを定義しています。今回は数字列の長さを100,200,300,…,4800,4900,5000と100刻みで100から5000までにしています。
5~19行目
for N in N_list:
for i in range(10): # 各Nに対して10回ソートする
t_m = []
t_b = []
A = [random.randint(0,100) for _ in range(N)] # ソートするリストを用意する
# マージソートの計算時間を記録する
start_time_m = time.time()
Merge_Sort(A)
end_time_m = time.time()
t_m.append(end_time_m-start_time_m)
# バブルソートの計算時間を記録する
start_time_b = time.time()
Bubble_Sort(A)
end_time_b = time.time()
t_b.append(end_time_b-start_time_b)
5行目ではさっき4行目で定義したN_list中の要素をfor文で回しています。
6行目ではN_list中の各要素に対して10回実験を行っています。つまり
「長さ100の数字列を10回ソートする」
「長さ200の数字列を10回ソートする」
・・・
「長さ4900の数字列を10回ソートする」
「長さ5000の数字列を10回ソートする」
という実験を行っています。
7,8行目では各Nに対して実験を10回行ったときの、マージソートとバブルソートの計算時間を保管しておくリストをそれぞれ作っています。
9行目ではソートするリストAを生成しています。リストは0以上100以下の整数をランダムにN個並べています。
11~13行目でマージソートの計算時間を計測して、14行目で保管リストに時間を追加しています。
16~18行目でバブルソートの計算時間を計測して、19行目で保管リストに時間を追加しています。
21~24行目
avg_time_m = sum(t_m)/len(t_m)
time_list_merge.append(avg_time_m)
avg_time_b = sum(t_b)/len(t_b)
time_list_bubble.append(avg_time_b)
21行目でマージソートの10回の実験結果の平均値を求め、22行目でtime_list_mergeに平均値を追加しています。
23行目でバブルソートの10回の実験結果の平均値を求め、24行目でtime_list_mergeに平均値を追加しています。
結果のグラフを表示する
## 結果のグラフを表示する
plt.figure(figsize = (10,6))
plt.plot(N_list,time_list_merge, marker = "o", color = "blue", label = "Merge Sort")
plt.plot(N_list,time_list_bubble, marker = "o", color = "red", label = "Bubble Sort")
plt.xlabel("length of list")
plt.ylabel("time (s)")
plt.legend()
plt.show()
ここでは実験結果を折れ線グラフとして表示しています。
「plt.plot(N_list,time_list_merge, marker = “o”, color = “blue”, label = “Merge Sort”)」でマージソートの計算時間の折れ線グラフを作ってます。「marker=”o”」でグラフに点が付き、「color=”blue”」でグラフの色を青にし、「label=”Merge Sort”」でラベルをMerge Sortとしています。
「plt.plot(N_list,time_list_bubble, marker = “o”, color = “red”, label = “Bubble Sort”)」でバブルソートの計算時間の折れ線グラフを作ってます。「marker=”o”」でグラフに点が付き、「color=”red”」でグラフの色を赤にし、「label=”Bubble Sort”」でラベルをBubble Sortとしています。
グラフを見て結果を解釈する

この図を見ると、明らかにバブルソートの方が計算時間がかかっているということが分かります。バブルソートはリストの長さが大きくなるにつれて計算時間が明確に大きくなっていて、長さ5000程度でソートするのに4秒ほどかかっています。
一方マージソートは長さ5000程度では計算時間はほぼ0秒であることが分かります。このことから計算時間において、マージソートはバブルソートよりも優れているということが分かります。
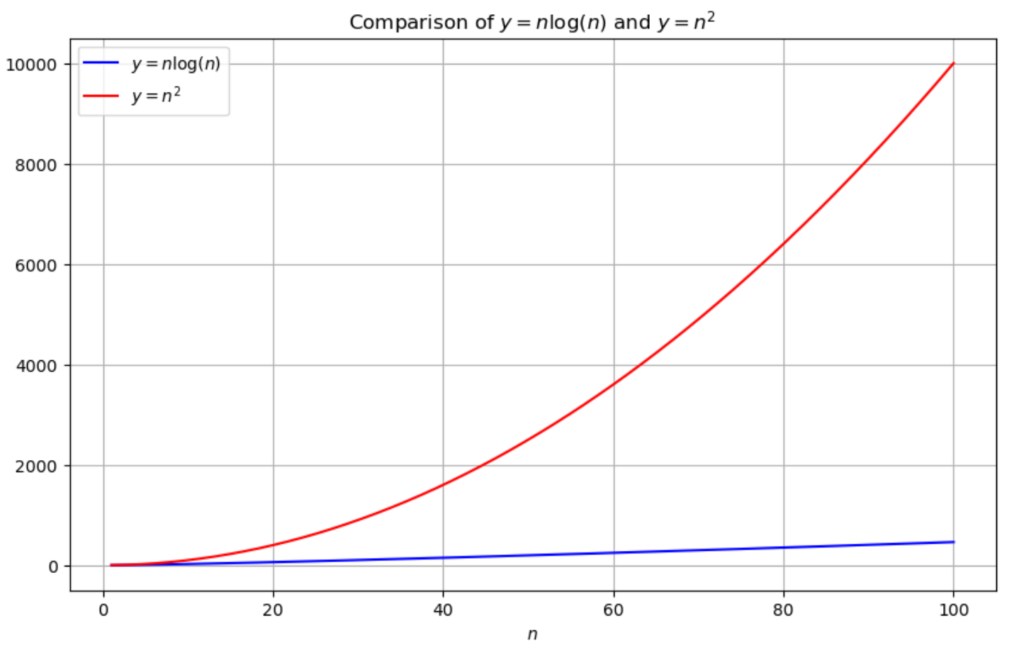
もう少し詳しく説明します。リストの長さを\(n\)とするとマージソートの計算量は\(O(n\log n)\)であるのに対し、バブルソートの計算量は\(O(n^2)\)であることが知られています。
そのためリストの長さが大きくなるにつれて2つのソートの計算時間は大きく変わってしまうのです。
もう少し数字列を長くしてマージソートの計算時間を測ってみる
それでは最後にもう少しだけ数字列を長くしてマージソートの計算時間を測ってみます。
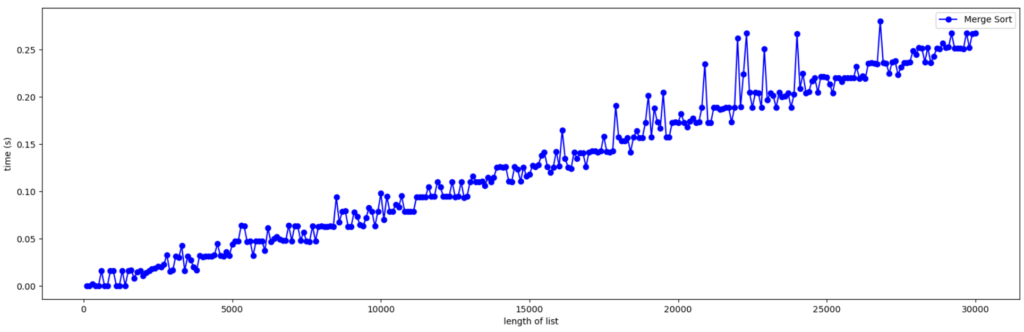
数字列の長さを100から30000まで100刻みにして、マージソートの計算時間を測ってグラフにしてみました。今回も各長さに対して10回計算して平均値を求めました。
これを見ると、バブルソートに比べたら緩やかですが数字列が長くなるにつれてマージソートも計算時間が大きくなっていることが分かります。それでも30000個の数字を並べるのに0.3秒くらいしかかかってないので結構速いですね。
おわりに
いかがでしたか。
今回の記事ではマージソートとバブルソートの計算時間について調べてみました。
今後もこのようなアルゴリズムに関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。





