- 巡回セールスマン問題ってなに?
- MTZ制約ってなに?
- MTZ制約を使うと計算時間が短くなるの?
こんにちは!しゅんです!
今回は巡回セールスマン問題とMTZ制約について解説していきます!
以前の記事で、MTZ制約を使って巡回セールスマン問題を定式化しましたが、そのときの説明でMTZ制約は制約の本数が少なくて済むという説明をしました。そこで今回の記事ではMTZ制約を使うと本当に計算時間が短くなるのかを検証してみたいと思います!
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
巡回セールスマン問題ってなに?

巡回セールスマン問題とは、スタート地点から全ての地点に丁度1回ずつ訪れてまたスタート地点に戻ってくるルートを考える問題です。
上の例で言うと紫色の〇がスタート地点で、全ての黄色の〇を通ってまた紫の〇に戻ってくるルートを考えます。

一番よくある問題は、
「移動距離が最小となるルートを求める」
という問題です。上図の2つのルートを見てみると、左側のルートの方が移動距離が短いように見えます。
この記事でも、考えられるルートの中で移動距離が最小となるようなルートを求める巡回セールスマン問題を考えていきたいと思います。
整数計画問題として定式化する
部分巡回路除去制約としてDFJ制約を使うパターンとMTZ制約を使うパターンの2つを紹介します。
DFJ制約を使って定式化する
パラメータ:
\(V\) : 地点の集合
\(d_{ij}\) : 地点 \(i\) と地点 \(j\) 間の距離
変数:
\(x_{ij} \in \{0,1\}\) : 地点 \(i\) から地点 \(j\) に向かうなら1、そうでないなら0を取る0-1変数
定式化:
\( \min \;\;\; \sum\limits_{i \in V}\sum\limits_{j \in V , i \ne j} d_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall i \in V)\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall j \in V)\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij} \leq |S| -1 \;\;\; (\forall S \subset V, |S| \geq 2)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;\; (\forall i \in V, \forall j \in V, i \ne j)\)
DFJ制約:
\(\sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij} \leq |S| -1 \;\;\; (\forall S \subset V, |S| \geq 2)\)
過去の記事で上の定式化について詳しく説明しているので、ここでは説明を省略します。
MTZ制約を使って定式化する
パラメータ:
\(V\) : 地点の集合
\(d_{ij}\) : 地点 \(i\) と地点 \(j\) 間の距離
変数:
\(x_{ij} \in \{0,1\}\) : 都市\(i\)から都市\(j\)に向かうなら1、そうでないなら0を取る0-1変数
\(y_{i}\) : MTZ制約で用いる連続変数
定式化:
\( \min \;\;\; \sum\limits_{i \in V}\sum\limits_{j \in V , i \ne j} d_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall i \in V)\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall j \in V)\)
\(\;\;\;\;\;\;\;\;\; y_{i}-y_{j}+|V|x_{ij} \leq |V|-1\)
\((\forall i \in V/\{0\}, \; \forall j \in V/\{0\}, \; i \ne j)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;\; (\forall i \in V, \forall j \in V, i \ne j)\)
MTZ制約:
\(y_{i}-y_{j}+|V|x_{ij} \leq |V|-1\)
\((\forall i \in V/\{0\}, \; \forall j \in V/\{0\}, \; i \ne j)\)
この定式化も過去の記事で詳しく説明しているので、ここでは説明を省略します。
2つの制約では制約の本数に差がある
今DFJ制約とMTZ制約の2つを紹介しましたが、この2つの制約の違いとして制約の本数が挙げられます。地点数が大きくなるとDFJ制約は地点数の指数オーダーで増加しますが、MTZ制約は地点数の多項式オーダーで増加します。
そのため直観的に考えたら
DFJ制約を使った定式化:計算時間 大
MTZ制約を使った定式化:計算時間 小
となりそうです。ということでこの記事では本当に計算時間に差が出るのかを確かめたいと思います!
MTZ制約を使うと計算時間がどうなるかpythonを使って検証してみた
それでは実際にpythonを使って計算時間がどうなるかを確かめてみましょう。検証に使うコードの説明と結果を図示して確認してみましょう。
検証は以下のように行いました。
検証方法
・地点数を2から16に変更してDFJ制約verとMTZ制約verのそれぞれで計算時間を計測する。
・各地点数に対して5回計算を行い、その平均値を出力する。
検証環境
プロセッサ:Intel(R) Core(TM) i5-1035G7 CPU @ 1.20GHz 1.50 GHz
実装RAM:16.0 GB
ソルバー:PULP_CBC_CMD
検証に使用したコードはけっこう長いので、結果だけ確認したい方は「結果をグラフで図示する」の所まで飛んでください。
コードの解説
## 必要なライブラリをインポート
import time
import random
import pulp
from pulp import LpMinimize, LpVariable, lpSum
from itertools import chain, combinations
random.seed(1)
## DFJ制約を用いて定式化して解く
def TSP_DFJ(V, subsets, d):
prob = pulp.LpProblem(sense = LpMinimize) # 問題を最小化に設定
x = LpVariable.dicts("x", [(i, j) for i in V for j in V if i != j], cat="Binary") # 変数xを定義
prob += lpSum(d[(i,j)] * x[i,j] for i in V for j in V if i != j) # 目的関数を設定
for i in V:
prob += lpSum(x[i,j] for j in V if i != j) == 1 # 1つ目の制約
for j in V:
prob += lpSum(x[i,j] for i in V if i != j) == 1 # 2つ目の制約
for S in subsets:
if 2 <= len(S) < len(V):
prob += lpSum(x[i,j] for i in S for j in S if i != j) <= len(S) - 1 # 3つ目の制約
start_time = time.time()
result = prob.solve() # 問題を解く
end_time = time.time()
elapsed_time = end_time - start_time # 計算時間を求める
return elapsed_time # 計算時間を返す
## MTZ制約を用いて定式化して解く
def TSP_MTZ(V, V_0, d):
prob = pulp.LpProblem(sense = LpMinimize) # 問題を最小化に設定
x = LpVariable.dicts("x", [(i, j) for i in V for j in V if i != j], cat="Binary") # 変数xを定義
y = LpVariable.dicts("y", V_0, cat="Continuous") # 変数yを定義
prob += lpSum(d[(i,j)] * x[i,j] for i in V for j in V if i != j) # 目的関数を定義
for i in V:
prob += lpSum(x[i,j] for j in V if i != j) == 1 # 1つ目の制約条件を設定
for j in V:
prob += lpSum(x[i,j] for i in V if i != j) == 1 # 2つ目の制約条件を設定
for i in V_0:
for j in V_0:
if i != j:
prob += y[i] - y[j] + len(V)*x[i,j] <= len(V) - 1 # 3つ目の制約条件を設定
start_time = time.time()
result = prob.solve() # 問題を解く
end_time = time.time()
elapsed_time = end_time - start_time # 計算時間を求める
return elapsed_time # 計算時間を返す
## Vの冪集合を返す関数を定義
def powerset(V):
return list(map(list, chain.from_iterable(combinations(V, r) for r in range(len(V)+1))))
## 地点数ごとの計算時間を求めて表示する
n_list= [n for n in range(2,17)] # 地点数(depoを含む)を2~16で計算する
time_list_DFJ = [] # DFJ制約verの計算時間を格納するリスト
time_list_MTZ = [] # MTZ制約verの計算時間を格納するリスト
for n in n_list: # for文でnをまわす
times_DFJ = [] # 各nでのDFJ制約verの計算時間を格納するリスト
times_MTZ = [] # 各nでのMTZ制約verの計算時間を格納するリスト
V = [i for i in range(n)] # 各地点のリスト
V_0 = V[1:] # 頂点を除いたリスト
subsets = powerset(V) # Vの冪集合を2次元リスト形式で設定
for _ in range(5): # 各nに対して5回計算する
pos = [(random.uniform(0,1), random.uniform(0,1)) for _ in range(n)] # 各地点の座標をランダムに生成する
d = {(i, j): ((pos[i][0]-pos[j][0])**2 + (pos[i][1]-pos[j][1])**2)**0.5
for i in range(n) for j in range(n) if i != j} # 都市間の距離を計算
times_DFJ.append(TSP_DFJ(V, subsets, d)) # 各nでの時間を格納するリストにDFJ制約verの計算時間を追加する
times_MTZ.append(TSP_MTZ(V, V_0 ,d)) # 各nでの時間を格納するリストにMTZ制約verの計算時間を追加する
avg_DFJ = sum(times_DFJ)/len(times_DFJ) # 5回の計算の平均値を計算する
avg_MTZ = sum(times_MTZ)/len(times_MTZ) # 5回の計算の平均値を計算する
time_list_DFJ.append(avg_DFJ) # DFJ制約verの計算時間を格納するリスト
time_list_MTZ.append(avg_MTZ) # MTZ制約verの計算時間を格納するリスト
print(f"{n}地点の計算が終了しました") # 計算が終了したことを知らせる
print(time_list_DFJ) # DFJ制約verの時間リストを表示する
print(time_list_MTZ) # MTZ制約verの時間リストを表示する
かなり長いので分割して説明します。
必要なライブラリをインポート
## 必要なライブラリをインポート
import time
import random
import pulp
from pulp import LpMinimize, LpVariable, lpSum
from itertools import chain, combinations
random.seed(1)
ここでは必要なライブラリをインポートします。
2行目では「time」をインポートしています。「time」は時間を計測するのに使います。
3行目では「random」をインポートしています。「random」は各地点の座標をランダムに設定するために使います。
4~5行目では「pulp」から「LpMinimize」、「LpVariable」、「lpSum」をインポートしています。「pulp」は数理計画問題を扱うために使います。
6行目では「itertools」から「chain」、「combinations」をインポートしています。これらはある集合の部分集合を取得するために使います。
7行目ではシード値を固定しています。これがあることで毎回同じ結果が出力されます。
DFJ制約を用いて定式化して解く
## DFJ制約を用いて定式化して解く
def TSP_DFJ(V, subsets, d):
prob = pulp.LpProblem(sense = LpMinimize) # 問題を最小化に設定
x = LpVariable.dicts("x", [(i, j) for i in V for j in V if i != j], cat="Binary") # 変数xを定義
prob += lpSum(d[(i,j)] * x[i,j] for i in V for j in V if i != j) # 目的関数を設定
for i in V:
prob += lpSum(x[i,j] for j in V if i != j) == 1 # 1つ目の制約
for j in V:
prob += lpSum(x[i,j] for i in V if i != j) == 1 # 2つ目の制約
for S in subsets:
if 2 <= len(S) < len(V):
prob += lpSum(x[i,j] for i in S for j in S if i != j) <= len(S) - 1 # 3つ目の制約
start_time = time.time()
result = prob.solve() # 問題を解く
end_time = time.time()
elapsed_time = end_time - start_time # 計算時間を求める
return elapsed_time # 計算時間を返す
ここではDFJ制約を用いて定式化して解いています。下記の定式化に従ってコードを書いています。
2行目で関数を定義しています。
3行目で問題を最小化に設定しています。問題の最小化は「LpMinimize」でできます。
4行目で0-1変数「x」を定義しています。引数は左から(変数名、添字の集合、変数の種類)となっています。上の書き方だと変数名が「x」、引数はリスト「V」中の要素「i」「j」の組合せ(「i」と「j」は異なる)、変数の種類は「Binary」(0-1変数)となります。
5行目で目的関数を設定しています。
6~7行目で1つ目の制約条件を設定しています。
8~9行目で2つ目の制約条件を設定しています。
10~12行目で3つ目の制約条件を設定しています。
13~16行目で計算時間を記録しています。14行目の「prob.solve()」で問題を解いており、13行目で計算開始時間、15行目で計算終了時間を記録し、16行目でその差分を求めて計算時間を取得しています。
17行目で計算時間を返しています。
パラメータ:
\(V\) : 地点の集合
\(d_{ij}\) : 地点 \(i\) と地点 \(j\) 間の距離
変数:
\(x_{ij} \in \{0,1\}\) : 地点 \(i\) から地点 \(j\) に向かうなら1、そうでないなら0を取る0-1変数
定式化:
\( \min \;\;\; \sum\limits_{i \in V}\sum\limits_{j \in V , i \ne j} d_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall i \in V)\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall j \in V)\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij} \leq |S| -1 \;\;\; (\forall S \subset V, |S| \geq 2)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;\; (\forall i \in V, \forall j \in V, i \ne j)\)
MTZ制約verについても同じことが言えますが、今回の目的はどんな解が得られたかを見ることではなく計算時間を求めることです。そのため返すものは解ではなく計算時間にしています。ちゃんとこのコードで最適解が得られることは確認済みです。
MTZ制約を用いて定式化して解く
## MTZ制約を用いて定式化して解く
def TSP_MTZ(V, V_0, d):
prob = pulp.LpProblem(sense = LpMinimize) # 問題を最小化に設定
x = LpVariable.dicts("x", [(i, j) for i in V for j in V if i != j], cat="Binary") # 変数xを定義
y = LpVariable.dicts("y", V_0, cat="Continuous") # 変数yを定義
prob += lpSum(d[(i,j)] * x[i,j] for i in V for j in V if i != j) # 目的関数を定義
for i in V:
prob += lpSum(x[i,j] for j in V if i != j) == 1 # 1つ目の制約条件を設定
for j in V:
prob += lpSum(x[i,j] for i in V if i != j) == 1 # 2つ目の制約条件を設定
for i in V_0:
for j in V_0:
if i != j:
prob += y[i] - y[j] + len(V)*x[i,j] <= len(V) - 1 # 3つ目の制約条件を設定
start_time = time.time() # 計算開始時刻を記録
result = prob.solve() # 問題を解く
end_time = time.time() # 計算終了時刻を記録
elapsed_time = end_time - start_time # 計算時間を求める
return elapsed_time # 計算時間を返す
ここではMTZ制約を用いて定式化して解いています。下記の定式化に従ってコードを書いています。
2行目で関数を定義しています。
3行目で問題を最小化に設定しています。問題の最小化は「LpMinimize」でできます。
4行目で0-1変数「x」を定義しています。引数は左から(変数名、添字の集合、変数の種類)となっています。上の書き方だと変数名が「x」、添字はリスト「V」中の要素「i」「j」の組合せ(「i」と「j」は異なる)、変数の種類は「Binary」(0-1変数)となります。
5行目で連続変数「y」を定義しています。各引数が何を表しているかは「x」のときと基本同じです。名前が「y」、添字はリスト「V_0」中の要素、変数の種類は「Continuous」(連続変数)となります。
6行目で目的関数を設定しています。
7~8行目で1つ目の制約条件を設定しています。
9~10行目で2つ目の制約条件を設定しています。
11~14行目で3つ目の制約条件を設定しています。
15~18行目で計算時間を記録しています。16行目の「prob.solve()」で問題を解いており、15行目で計算開始時間、17行目で計算終了時間を記録し、18行目でその差分を求めて計算時間を取得しています。
19行目で計算時間を返しています。
パラメータ:
\(V\) : 地点の集合
\(d_{ij}\) : 地点 \(i\) と地点 \(j\) 間の距離
変数:
\(x_{ij} \in \{0,1\}\) : 都市\(i\)から都市\(j\)に向かうなら1、そうでないなら0を取る0-1変数
\(y_{i}\) : MTZ制約で用いる連続変数
定式化:
\( \min \;\;\; \sum\limits_{i \in V}\sum\limits_{j \in V , i \ne j} d_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall i \in V)\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall j \in V)\)
\(\;\;\;\;\;\;\;\;\; y_{i}-y_{j}+|V|x_{ij} \leq |V|-1\)
\((\forall i \in V/\{0\}, \; \forall j \in V/\{0\}, \; i \ne j)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;\; (\forall i \in V, \forall j \in V, i \ne j)\)
Vの冪集合を返す関数を定義
## Vの冪集合を返す関数を定義
def powerset(V):
return list(map(list, chain.from_iterable(combinations(V, r) for r in range(len(V)+1))))
ここではVの冪集合を2次元リスト型で返す関数を定義しています。例えばこの関数に
V = [0,1,2,3]を入力すると
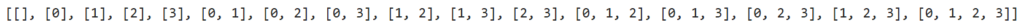
が返されます。
もう少し詳しく説明すると、「combinations(V,r)」を使ってリスト「V」から「r」個の要素を選ぶときの選び方を列挙しています。冪集合は「r = 0」から「r = len(V)」まで「combinations(V,r)」で得られたものを合わせればよいので「for r in range(len(V)+1)」で「r」を回しています。例えば
V = [0,1,2,3]
print(list(combinations(V, 2)))というコードを実行すると
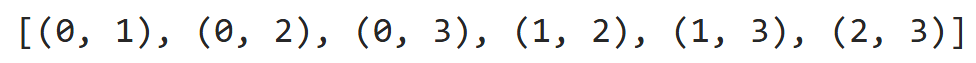
上図のように出力されます。
「chain.from_iterable()」を使えば複数のリストの要素を1つにまとめることができます。例えば
V = [0,1,2,3]
print(list(chain.from_iterable(combinations(V, r) for r in range(len(V)+1))))というコードを実行すると
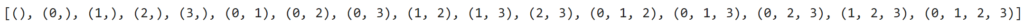
上図のように出力されます。
「map(list,~)」を使えば「~」中の要素をリスト型に変更することができます。「chain.from_iterable(combinations(V, r) for r in range(len(V)+1))」中の要素はタプルなのでこれをリストに変更します。以上より
V = [0,1,2,3]
print(list(map(list, chain.from_iterable(combinations(V, r) for r in range(len(V)+1)))))というコードを実行すると
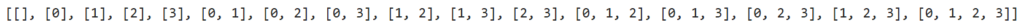
上図のように出力されます。
地点数ごとの計算時間を求めて表示する
## 地点数ごとの計算時間を求めて表示する
n_list= [n for n in range(2,17)] # 地点数(depoを含む)を2~16で計算する
time_list_DFJ = [] # DFJ制約verの計算時間を格納するリスト
time_list_MTZ = [] # MTZ制約verの計算時間を格納するリスト
for n in n_list: # for文でnをまわす
times_DFJ = [] # 各nでのDFJ制約verの計算時間を格納するリスト
times_MTZ = [] # 各nでのMTZ制約verの計算時間を格納するリスト
V = [i for i in range(n)] # 各地点のリスト
V_0 = V[1:] # 頂点を除いたリスト
subsets = powerset(V) # Vの冪集合を2次元リスト形式で設定
for _ in range(5): # 各nに対して5回計算する
pos = [(random.uniform(0,1), random.uniform(0,1)) for _ in range(n)] # 各地点の座標をランダムに生成する
d = {(i, j): ((pos[i][0]-pos[j][0])**2 + (pos[i][1]-pos[j][1])**2)**0.5
for i in range(n) for j in range(n) if i != j} # 都市間の距離を計算
times_DFJ.append(TSP_DFJ(V, subsets, d)) # 各nでの時間を格納するリストにDFJ制約verの計算時間を追加する
times_MTZ.append(TSP_MTZ(V, V_0 ,d)) # 各nでの時間を格納するリストにMTZ制約verの計算時間を追加する
avg_DFJ = sum(times_DFJ)/len(times_DFJ) # 5回の計算の平均値を計算する
avg_MTZ = sum(times_MTZ)/len(times_MTZ) # 5回の計算の平均値を計算する
time_list_DFJ.append(avg_DFJ) # DFJ制約verの計算時間を格納するリスト
time_list_MTZ.append(avg_MTZ) # MTZ制約verの計算時間を格納するリスト
print(f"{n}地点の計算が終了しました") # 計算が終了したことを知らせる
print(time_list_DFJ) # DFJ制約verの時間リストを表示する
print(time_list_MTZ) # MTZ制約verの時間リストを表示する
この部分ではこれまで定義してきた関数を使って計算時間を計測しています。
2行目で地点数のリストを作成しています。今回はデポ含んだ地点数が2~16の場合について巡回セールスマン問題を解いて計算時間を計測しようと思います。
3行目でDFJ制約を使った場合の計算時間を格納するリストの初期設定をしています。
4行目でDFJ制約を使った場合の計算時間を格納するリストの初期設定をしています。
5行目では2行目で生成した「n_list」からfor文で1つずつ要素を取り出しています。
6行目では各「n」に対してランダムに生成した5個の問題をDFJ制約verで解いたときの計算時間を格納するリストの初期設定をています。
7行目では各「n」に対してランダムに生成した5個の問題をMTZ制約verで解いたときの計算時間を格納するリストの初期設定をています。
8行目では地点のリスト「V」を生成しています。
9行目ではデポを除いた地点のリスト「V_0」を生成しています。
10行目では「V」の冪集合を取得しています。
11行目では各「n」に対してfor文で5回それ以降の計算を行っています。
12行目では各地点の座標をランダムに生成しています。「random.uniform(0,1)」で0以上1以下の実数をランダムに出力しています。
13~14行目で2地点間のユークリッド距離を辞書形式で計算しています。
15行目ではDFJ制約verの計算時間を取得して6行目で生成したリストに追加しています。
16行目ではMTZ制約verの計算時間を取得して7行目で生成したリストに追加しています。
17行目ではDFJ制約verの計算時間5回の平均値を求めています。
18行目ではMTZ制約verの計算時間5回の平均値を求めています。
19行目では3行目で生成したリストに平均値を追加しています。
20行目では4行目で生成したリストに平均値を追加しています。
21行目では「n」地点の計算が完了したことを知らせています。
22行目ではDFJ制約verの計算時間を格納したリストを表示しています。
23行目ではMTZ制約verの計算時間を格納したリストを表示しています。
結果をグラフで図示する
このコードを実行すると下図の結果が得られました。
1~15行目までは各地点数における計算が終了したことを知らせています。
16~17行目がDFJ制約verの計算時間、18~19行目がMTZ制約verの計算時間をそれぞれ表しています。
と言っても文字だけじゃよく分からないのでグラフで図示してみましょう。
import matplotlib.pyplot as plt
plt.figure(figsize = (8,5))
plt.plot(n_list, time_list_DFJ, marker = "o", color = "hotpink", label = "DFJ constraint")
plt.plot(n_list, time_list_MTZ, marker = "o", color = "lightskyblue", label = "MTZ constraint")
plt.xticks(n_list)
plt.xlabel("number of cities")
plt.ylabel("time (s)")
plt.grid()
plt.legend()
plt.show()
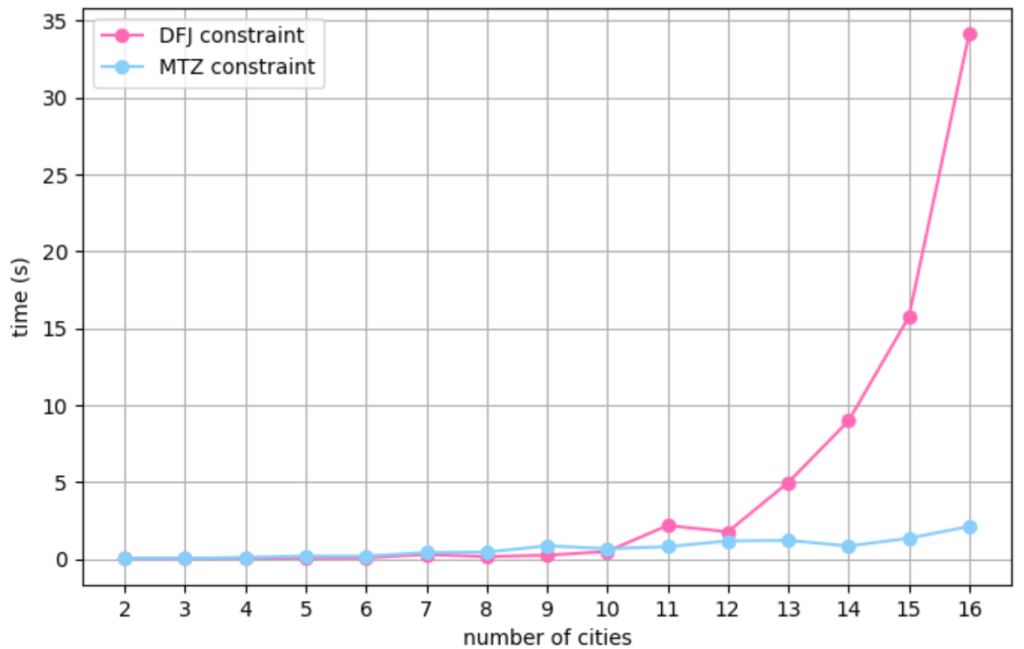
これを見ると地点数が13辺りから違いが顕著に表れています。やはり想定通りDFJ制約を使う方が計算時間が長くなりました。
16地点におけるそれぞれの計算時間を見てみると
16地点におけるそれぞれの計算時間
DFJ制約:約34.12秒
MTZ制約:約2.11秒
となり、MTZ制約を使えば30秒以上も計算時間が短くなるという結果になりました。
おわりに
いかがでしたか。
今回の記事では巡回セールスマン問題について解説しました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。





