- MTZ制約ってなに?
- MTZ制約を使って巡回セールスマン問題を定式化したい…
- 巡回セールスマン問題をpythonで解きたい…
こんにちは!しゅんです!
今回はMTZ制約を使って巡回セールスマン問題を解いてみたいと思います。
この記事ではMTZ制約が意味していること、定式化の方法、pythonでの解き方を紹介しています。
それではやっていきましょう!
組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
今回解く問題の設定
それではまず最初に今回考えたい問題をちゃんと設定しましょう
問題設定
・世界一周旅行を行う。
・東京から出発して合計5カ国を回ってまた東京に戻ってくる。
・旅行で行く都市は以下の通りである。
ニューヨーク(アメリカ)
ブエノスアイレス(アルゼンチン)
ソウル(韓国)
ロンドン(イギリス)
カイロ(エジプト)
目的
移動距離の合計が最小となるような旅行ルートを求めたい。
例えば以下のような旅行ルートがあります。
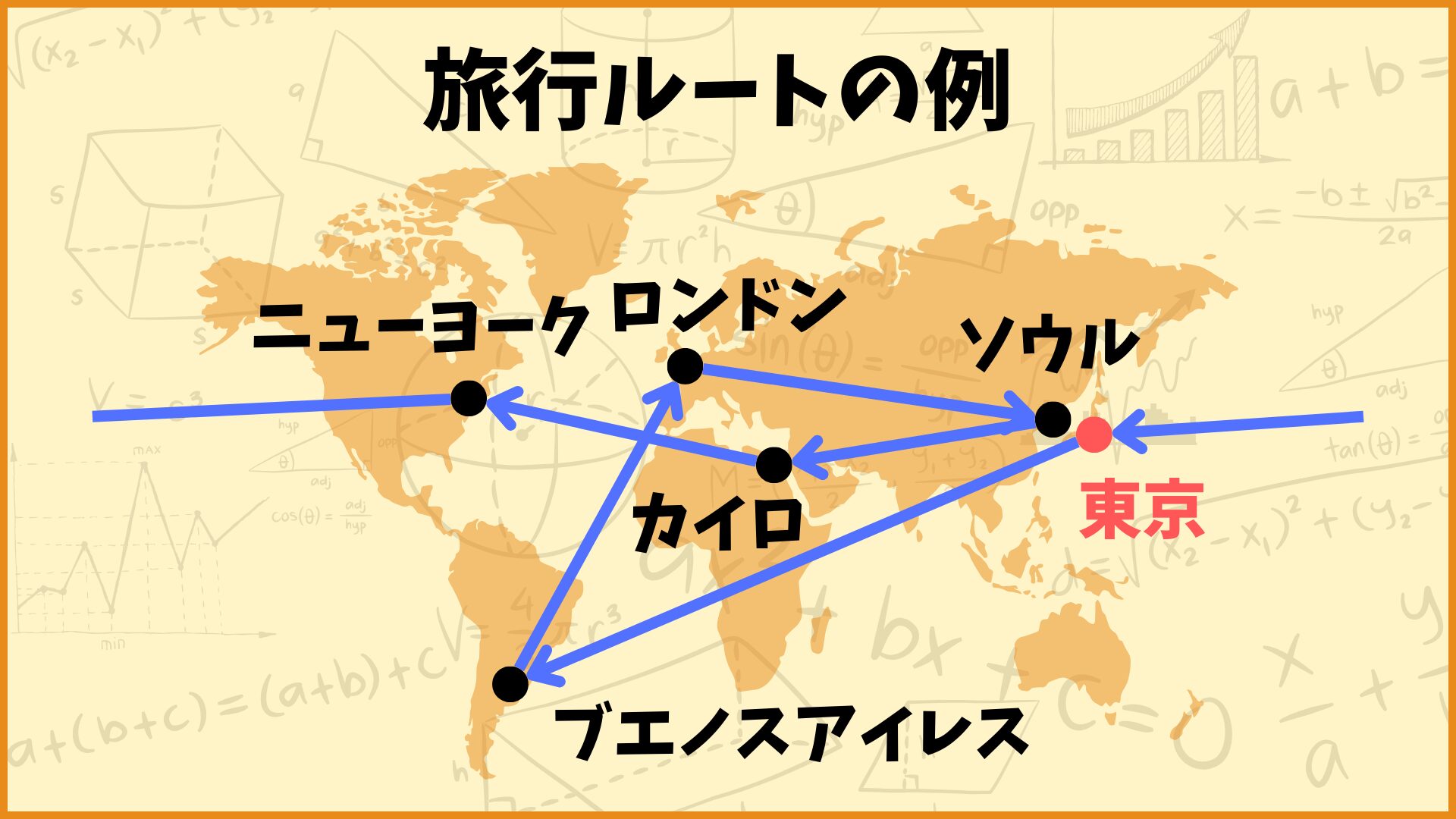
上図の例は
東京→ブエノスアイレス→ロンドン→ソウル→カイロ→ニューヨーク→東京
の旅行ルートです。
現実の旅行ではおそらく他にも色々考えてルートを決めると思いますが、今回は単純に移動距離の合計が最小となる旅行ルートを考えます。
整数計画問題として定式化
「記号の設定」、「目的関数の設定」、「制約条件の設定」の3つに分けて説明したいと思います。
記号の設定
パラメータとして都市の集合と各都市間の距離を設定します。変数は0-1変数\(x_{ij}\)と連続変数\(y_i\)を使いたいと思います。
パラメータ:
\(V = \{0,1,2,3,4,5\}\) : 都市の集合
\(d_{ij}\) : 都市 \(i\) と都市 \(j\) 間の距離
変数:
\(x_{ij} \in \{0,1\}\) : 都市 \(i\) から都市 \(j\) に向かうなら1、そうでないなら0を取る0-1変数
\(y_{i}\) : MTZ制約で用いる連続変数
なお、各都市と数字の対応は以下の通りです。
0 : 東京
1 : ニューヨーク
2 : ブエノスアイレス
3 : ソウル
4 : ロンドン
5 : カイロ
各都市間の距離は以下のサイトを使って求めました。
2都市間の距離と方位角 – 高精度計算サイト (casio.jp)
目的関数の設定
この問題の目的は
「移動距離の合計が最小となるような旅行ルートを求めたい」
です。よって以下のように表すことができます。
目的関数:
\(\sum\limits_{i \in V}\sum\limits_{j \in V , i \ne j} d_{ij}x_{ij} \)
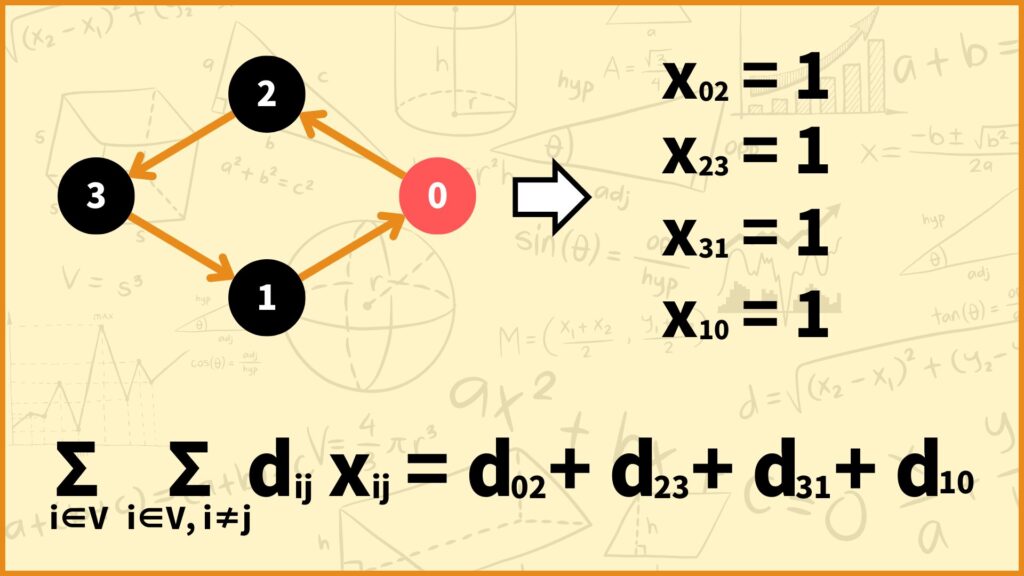
例えば \(V = \{0,1,2,3\}\) だとして0→2→3→1→0の順に回るとします。このとき変数の値は
\(x_{02} = x_{23} = x_{31} = x_{10} = 1\)
で他の変数の値は0となります。また目的関数値は
\(\sum\limits_{i \in V}\sum\limits_{j \in V , i \ne j} d_{ij}x_{ij}\)
\( = d_{02}x_{02} + d_{23}x_{23} + d_{31}x_{31} + d_{10}x_{10}\)
\( = d_{02}+d_{23}+d_{31}+d_{10}\)
となります。この値はこの旅行ルートの移動距離の合計と対応しています。回る都市の数 \(|V|\) が変わっても同じように考えることができます。今回はこれを最小化します。
2つ目の \(\sum\) の所が \(i \ne j\) となっているのは自己ループを防ぐためです。仮に \(x_{22} = 1\) とすると都市2から都市2に向かうということになってしまいます。
この後の「pythonで解いてみる」の所でも説明しますが、そもそも変数を作る段階で \(x_{ii} \; (\forall i \in V)\) は作らないので \(i \ne j\) としないとエラーが出てしまいます。今後登場する \(i \ne j\) はすべて同じ理由です。
今回はこの目的関数を最小化する問題を考えます。
\( \min \;\;\; \sum\limits_{i \in V}\sum\limits_{j \in V , i \ne j} d_{ij}x_{ij} \)
制約条件の設定
制約条件:
\(\sum\limits_{j \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall i \in V)\) → ①
\(\sum\limits_{i \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall j \in V)\) → ②
\(y_{i}-y_{j}+|V|x_{ij} \leq |V|-1\)
\((\forall i \in V/\{0\}, \; \forall j \in V/\{0\}, \; i \ne j)\) → ③
3つ目の制約がMTZ制約です。1つずつ解説していきます。
1つ目の制約
1つ目の制約:
\(\sum\limits_{j \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall i \in V)\)
1つ目の制約は「全ての都市に関して、必ずその都市から別の1つの都市に向かう」ことを表しています。
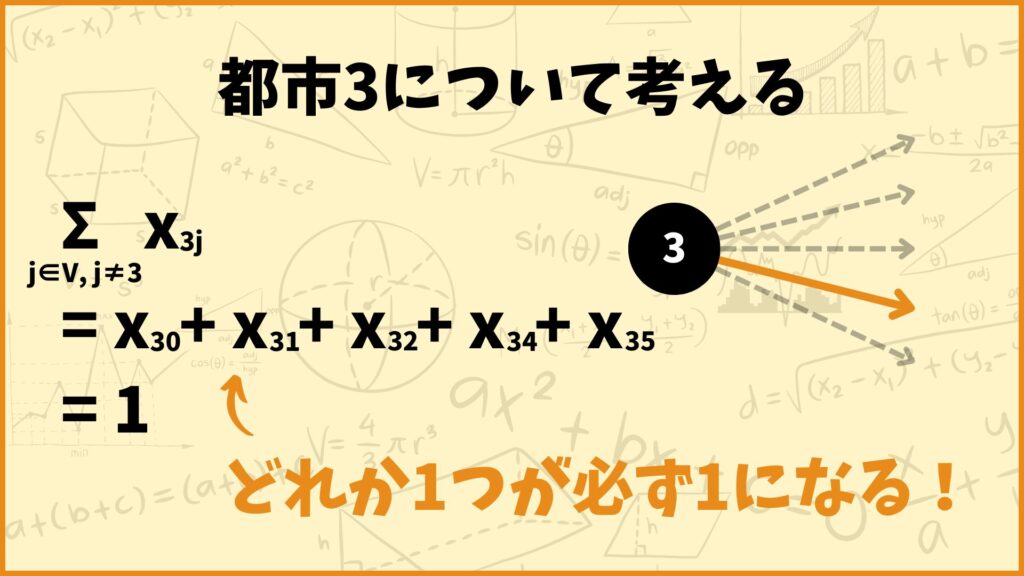
例えば都市3(ソウル)について考えてみましょう。制約式の左辺は
\(\sum\limits_{j \in V, j \ne 3}x_{3j}\)
\( = x_{30} + x_{31} + x_{32} + x_{34} + x_{35}\)
となります。変数 \(x_{ij}\) は0か1しか取らないので、制約式が成り立つためには上記の5個の変数のうちどれか1つだけが1を取ることを表します。これは
「必ず都市3から他の都市に向かう」
「都市3から2つ以上の都市に訪れることはできない」
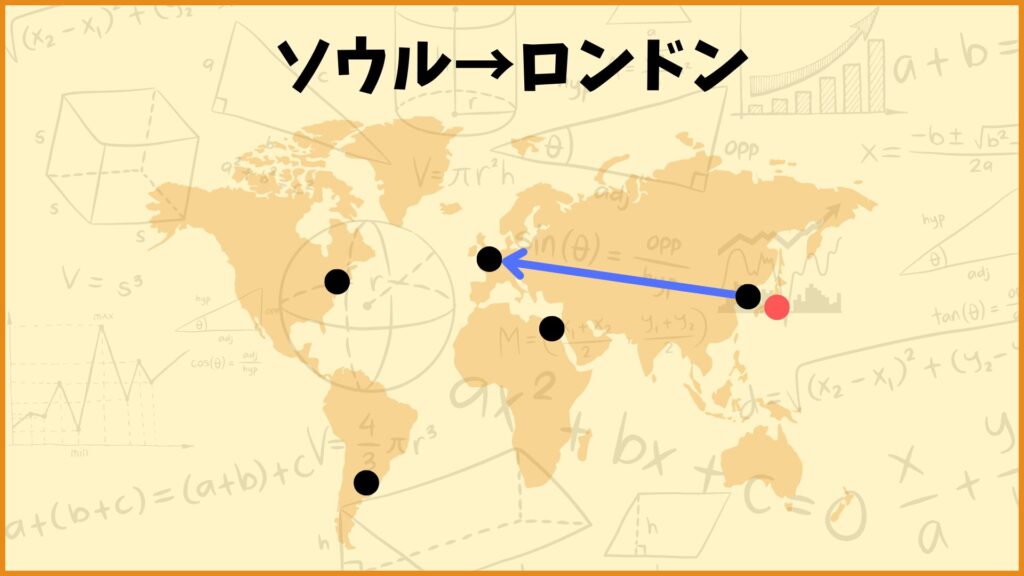
ということを表しています。例えば \(x_{34} = 1\) としましょう。これは
「都市3(ソウル)から都市4(ロンドン)に向かう」
ということを表しています。
2つ目の制約
2つ目の制約:
\(\sum\limits_{i \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall j \in V)\)
2つ目の制約は「全ての都市に関して、別の都市のうちどれか1つから必ずその都市に向かう」ことを表しています。
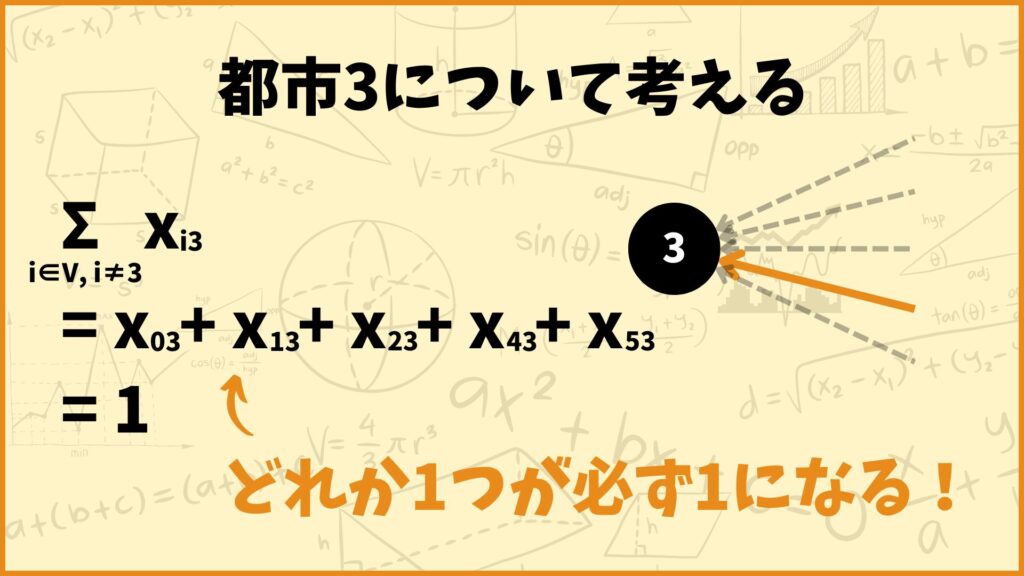
これも例えば都市3(ソウル)について考えてみましょう。制約式の左辺は
\(\sum\limits_{i \in V, i \ne 3}x_{i3}\)
\( = x_{03} + x_{13} + x_{23} + x_{43} + x_{53}\)
となります。変数 \(x_{ij}\) は0か1しか取らないので、制約式が成り立つためには上記の5個の変数のうちどれか1つだけが1を取ることを表します。これは
「必ず他の都市から都市3に向かう」
「2つ以上の都市から都市3に向かうことはできない」
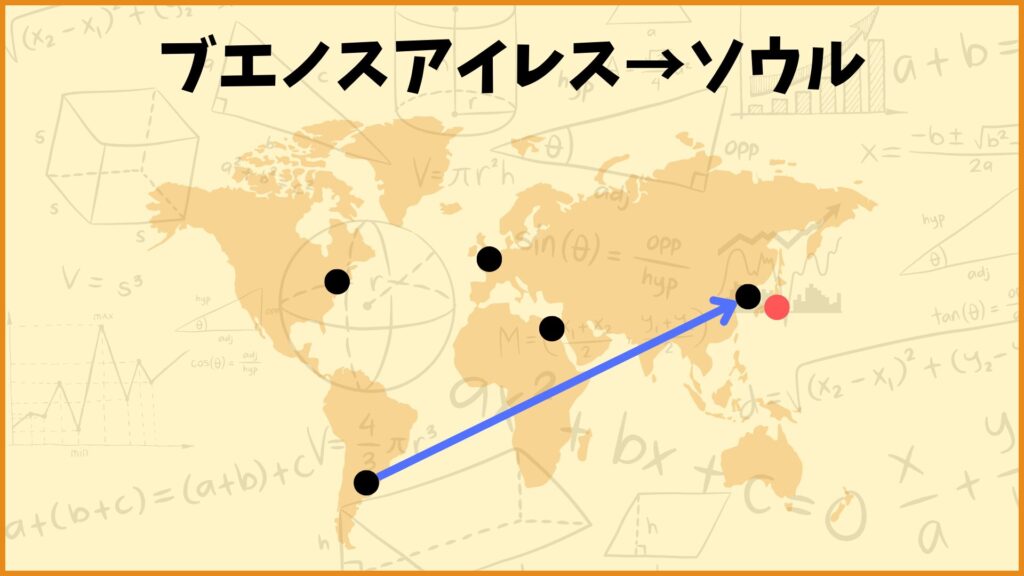
ということを表しています。例えば \(x_{23} = 1\) としましょう。これは
「都市2(ブエノスアイレス)から都市3(ソウル)に向かう」
ということを表しています。
3つ目の制約
3つ目の制約:
\(y_{i}-y_{j}+|V|x_{ij} \leq |V|-1\)
\((\forall i \in V/\{0\}, \; \forall j \in V/\{0\}, \; i \ne j)\)
3つ目の制約はMTZ制約という部分巡回路除去制約です。
部分巡回路とMTZ制約がなんなのかについては第4節の所で詳しく説明しています。
整数計画問題としてまとめる
以上のことを踏まえて整数計画問題として定式化しましょう。
パラメータ:
\(V = \{0,1,2,3,4,5\}\) : 都市の集合
\(d_{ij}\) : 都市\(i\)と都市\(j\)間の距離
変数:
\(x_{ij} \in \{0,1\}\) : 都市\(i\)から都市\(j\)に向かうなら1、そうでないなら0を取る0-1変数
\(y_{i}\) : MTZ制約で用いる連続変数
定式化:
\( \min \;\;\; \sum\limits_{i \in V}\sum\limits_{j \in V , i \ne j} d_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall i \in V)\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall j \in V)\)
\(\;\;\;\;\;\;\;\;\; y_{i}-y_{j}+|V|x_{ij} \leq |V|-1\)
\((\forall i \in V/\{0\}, \; \forall j \in V/\{0\}, \; i \ne j)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;\; (\forall i \in V, \forall j \in V, i \ne j)\)
ということで巡回セールスマン問題(travelling salesman problem)を整数計画問題として定式化することができました。
部分巡回路ってなに?
それでは先ほど説明を飛ばしたMTZ制約について説明していきます。MTZ制約を理解するためにはまず部分巡回路が何なのかを知っておく必要があるので、まず部分巡回路について説明します。
部分巡回路ってなに?
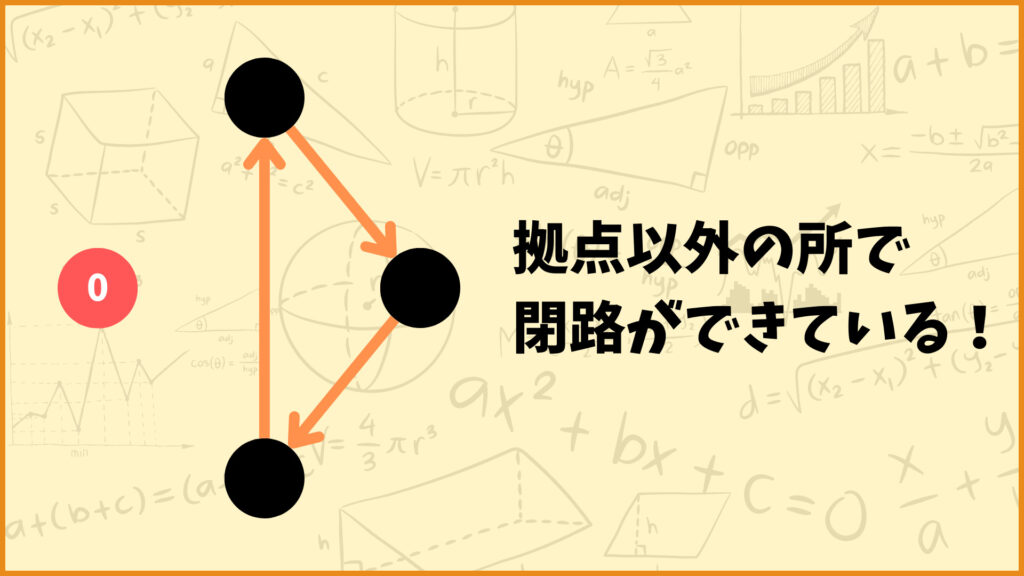
部分巡回路は上図のようなルートです。本当は拠点からスタートして拠点に戻ってくるルートを考えたいのですが、上図は拠点以外の所で閉路ができています。これが部分巡回路です。
旅行ルートの最適化では部分巡回路はできてほしくないので、部分巡回路を除去する必要があります。
MTZ制約は部分巡回路を除去する制約
MTZ制約:
\(y_{i}-y_{j} + |V|x_{ij} \leq |V|-1\)
\((\forall i \in V/\{0\}, \; \forall j \in V/\{0\}, \; i \ne j)\)
上記の制約で部分巡回路を除去することができます。この制約をMTZ制約と言います。それではなぜこの制約で部分巡回路を除去できるのかを説明していきます。
前提として \(x_{ij} = 0\) の場合、つまり地点 \(i\) から地点 \(j\) に行かない場合MTZ制約は
\(y_{i}-y_{j} \leq |V|-1 = 6-1 = 5\)
と表せます。ですが右辺の値が大きいので今回の問題においてこれは制約として意味を持たないです。そのため以下では \(x_{ij} = 1\) の場合に関して考えます。

例えば地点3から地点4に向かう場合を考えましょう。このとき \(x_{34} = 1\) となるのでMTZ制約は
\(y_{3}-y_{4} +|V| \times 1 \leq |V|-1\)
\(\Leftrightarrow y_{3}-y_{4} \leq-1\)
となります。この式から \(y_3\) より \(y_4\) の方が大きいことが分かります。つまりMTZ制約のイメージとしては
「\(y_i\) が小さい程初めの方に到達する都市である」
って感じです。これを踏まえて部分巡回路を持たない場合と持つ場合の両方について考えてみましょう。
部分巡回路を持たない場合
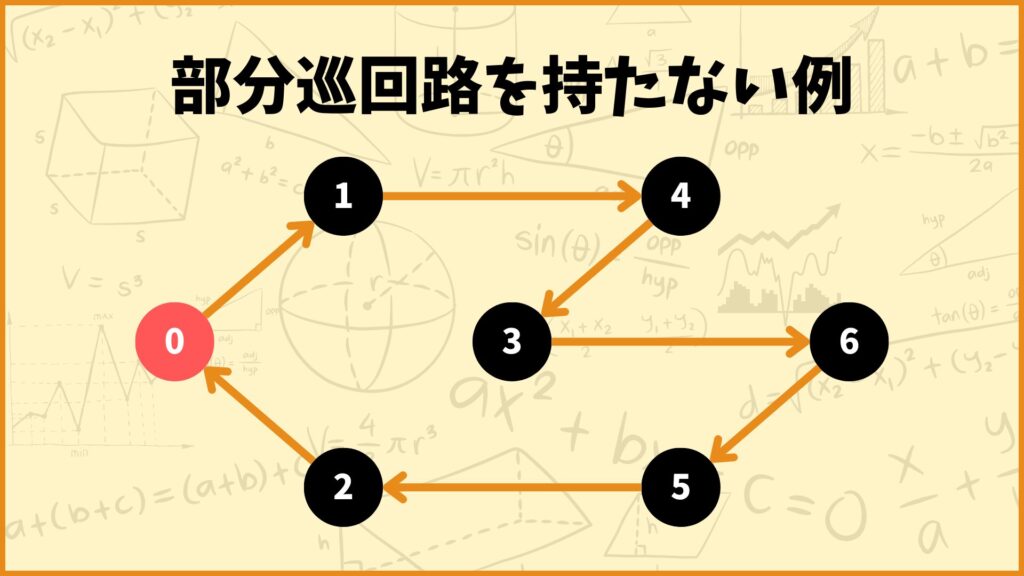
上記のようなルートを考えると、
\(x_{01} = x_{14} = x_{13} = x_{36} = x_{65} = x_{52} = x_{20} = 1\)
となります。よってMTZ制約は
\(y_{1}-y_{4} \leq -1\)
\(y_{4}-y_{3} \leq -1\)
\(y_{3}-y_{6} \leq -1\)
\(y_{6}-y_{5} \leq -1\)
\(y_{5}-y_{2} \leq -1\)
となります。例えば各都市の到達順に
\((y_1,y_2,y_3,y_4,y_5,y_6) = (1,6,3,2,5,4)\)
とすればMTZ制約を満たします。(代入すると不等式が成立していることが分かります。)
部分巡回路を持つ場合
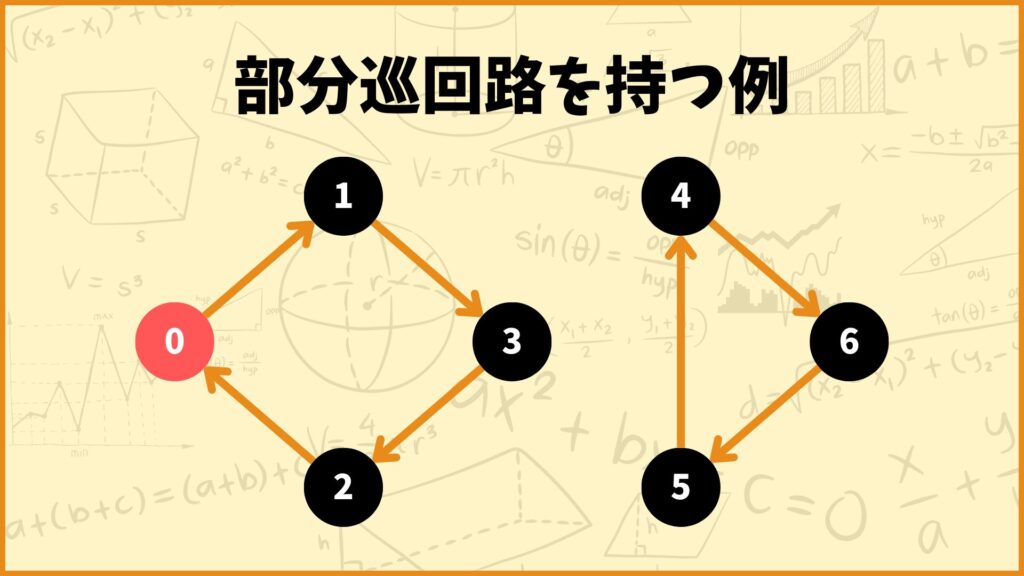
上図は制約式①,②を満たすルートですが4→6→5→4の部分巡回路を持っています。
このとき \(x_{46} = x_{65} = x_{54} = 1\) となりMTZ制約は
\(y_{4}-y_{6} \leq -1\)
\(y_{6}-y_{5} \leq -1\)
\(y_{5}-y_{4} \leq -1\)
となります。ちょっと考えてみると上の式を満たす \(y_4,y_5,y_6\) が存在しないことが分かります。というわけで部分巡回路を除去できるという訳です。
3つの不等式を全部足すと
\((y_4 – y_6) + (y_6 -y_5) + (y_5-y_4) = 0 \leq -1 -1 -1 = -3\)
と矛盾した式が得られます。
MTZ制約の利点ってなに?
MTZ制約の利点は
「制約の本数が少なくて済む」
ということです。もっとちゃんと言うと、旅行で行く都市の数が増えても制約の本数が多項式オーダーでしか増加しないというのがMTZ制約の利点です。
MTZ制約の本数:\(|V|^2 -3|V| + 2\)本
MTZ制約の本数を実際に数えてみましょう。制約式の本数は \(\forall i \in V/\{0\}, \; \forall j \in V/\{0\}, \; i \ne j\)を満たす \(i,\;j\) の組合せの数だけ存在します。
\(|V/\{0\}|=|V|-1\) なので \(\forall i \in V/\{0\}, \; \forall j \in V/\{0\}\) を満たす \(i,j\) の組合せの数は
\((|V|-1)^2 = |V|^2 -2|V| + 1\) → (※)
となります。ここから \(i =j\) となるの組合せの数を引き算すればOKです。\(i = j\) を満たす\(i,j\) の組合せの数は \(|V/\{0\}| = |V|-1\) 個なので(※)の式から引き算すればMTZ制約の本数は
\((|V|-1)^2 – (|V|-1) = |V|^2 -3|V| + 2\)
となることが分かります。つまり訪れる都市の数が増えてもそこまでMTZ制約の本数は増えないということが分かります。
部分巡回路除去制約はMTZ制約の他にもいくつかあります。例えば下記の制約式はDFJ制約と呼ばれる部分巡回路除去制約です。
\(\sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij} \leq |S| -1 \;\;\; (\forall S \subset V, |S| \geq 2)\)
DFJ制約の本数は\(2^{|V|}-|V|-2\)本なので訪れる都市の数が大きくなると制約式が指数オーダーで増加してしまいます。
具体的に本数を求めてみると
MTZ制約
\(|V| = 6 \Rightarrow 6^2-3\times 6 + 2 = 20\)本
\(|V| = 10 \Rightarrow 2^{10}-10-2 = 72\)本
\(|V| = 15 \Rightarrow 2^{15}-15-2 = 182\)本
\(|V| = 20 \Rightarrow 2^{20}-20-2 = 342\)本
DFJ制約
\(|V| = 6 \Rightarrow 2^6-6-2 = 56\)本
\(|V| = 10 \Rightarrow 2^{10}-10-2 = 1012\)本
\(|V| = 15 \Rightarrow 2^{15}-15-2 = 32751\)本
\(|V| = 20 \Rightarrow 2^{20}-20-2 = 1048554\)本
となります。都市の数が大きくなると違いがはっきりしますね。制約式の本数が多い程計算時間が長くなるのでMTZ制約を使うと計算時間を少なくすることができます。
pythonで解いてみる
それでは実際にこの問題をpythonで解いてみましょう。以下のプログラムを実行することで問題を解くことができます。
## 事前準備
from pulp import *## 記号の設定
V = [0,1,2,3,4,5]
V_0 = [1,2,3,4,5]
## 各都市間の距離を設定
d = {}
d[0,1] = 10862
d[0,2] = 18388
d[0,3] = 1152
d[0,4] = 9570
d[0,5] = 9575
d[1,2] = 8536
d[1,3] = 11070
d[1,4] = 5577
d[1,5] = 9030
d[2,3] = 19454
d[2,4] = 11142
d[2,5] = 11829
d[3,4] = 8873
d[3,5] = 8498
d[4,5] = 3513
# 距離dを対称にする
for i in V:
for j in V:
if i > j:
d[i,j] = d[j,i]## 整数計画問題として定式化したものを解く
prob = pulp.LpProblem(sense = LpMinimize)
x = LpVariable.dicts("x", [(i, j) for i in V for j in V if i != j], cat="Binary")
y = LpVariable.dicts("y", V_0, cat="Continuous")
prob += lpSum(d[(i,j)] * x[i,j] for i in V for j in V if i != j)
for i in V:
prob += lpSum(x[i,j] for j in V if i != j) == 1
for j in V:
prob += lpSum(x[i,j] for i in V if i != j) == 1
for i in V_0:
for j in V_0:
if i != j:
prob += y[i] - y[j] + len(V)*x[i,j] <= len(V) - 1
result = prob.solve()
## 結果の表示
print(LpStatus[result]) # 解の状態を表示
# 最適解の表示(値が1の変数だけ表示)
for i in V:
for j in V:
if i != j:
if x[i,j].value() == 1:
print(f"x_{i}_{j} =", x[i,j].value())
print("最適値 :",prob.objective.value()) # 最適値の表示
これらのプログラムを実行したら上の結果が得られました。それでは1つずつ説明していきます。
プログラムの説明
事前準備
## 事前準備
from pulp import *
問題を解く前に必要なライブラリをインポートしましょう。「pulp」はpythonで数理計画問題を解くのに使います。
記号の設定
## 記号の設定
V = [0,1,2,3,4,5]
V_0 = [1,2,3,4,5]
# # 各都市間の距離を設定
d = {}
d[0,1] = 10862
d[0,2] = 18388
d[0,3] = 1152
d[0,4] = 9570
d[0,5] = 9575
d[1,2] = 8536
d[1,3] = 11070
d[1,4] = 5577
d[1,5] = 9030
d[2,3] = 19454
d[2,4] = 11142
d[2,5] = 11829
d[3,4] = 8873
d[3,5] = 8498
d[4,5] = 3513
# 距離dを対称にする
for i in V:
for j in V:
if i > j:
d[i,j] = d[j,i]
次に記号の設定の所を説明します。
2行目では都市の集合を設定しています。各数字が表している年は以下の通りです。
0 : 東京
1 : ニューヨーク
2 : ブエノスアイレス
3 : ソウル
4 : ロンドン
5 : カイロ
3行目では \(V/\{0\}\) を設定しています。
6~21行目では各都市間の距離を設定しています。単位はkmで距離の計算は以下のサイトで行っています。
2都市間の距離と方位角 – 高精度計算サイト (casio.jp)
24~27行目では \(d_{ij} = d_{ji}\) と設定しています。
整数計画問題として定式化したものを解く
## 整数計画問題として定式化したものを解く
prob = pulp.LpProblem(sense = LpMinimize)
x = LpVariable.dicts("x", [(i, j) for i in V for j in V if i != j], cat="Binary")
y = LpVariable.dicts("y", V_0, cat="Continuous")
prob += lpSum(d[(i,j)] * x[i,j] for i in V for j in V if i != j)
for i in V:
prob += lpSum(x[i,j] for j in V if i != j) == 1
for j in V:
prob += lpSum(x[i,j] for i in V if i != j) == 1
for i in V_0:
for j in V_0:
if i != j:
prob += y[i] - y[j] + len(V)*x[i,j] <= len(V) - 1
# 問題を解く
result = prob.solve()
## 結果の表示
print(LpStatus[result]) # 解の状態を表示
# 最適解の表示(値が1の変数だけ表示)
for i in V:
for j in V:
if i != j:
if x[i,j].value() == 1:
print(f"x_{i}_{j} =", x[i,j].value())
print("最適値 :",prob.objective.value()) # 最適値の表示
2行目で問題を最小化に設定しています。
4行目で0-1変数 \(x_{ij}\) の定義をしています。\(i \ne j\) にしたいので「if i != j」としています。これ以降に出てくる「if i != j」はすべて同じ意味です。
5行目で連続変数 \(y_i\) の定義をしています。
7行目で目的関数を設定しています。
9~10行目で1つ目の制約条件
\(\sum\limits_{j \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall i \in V)\)
を設定しています。
12~13行目では2つ目の制約条件
\(\sum\limits_{i \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall j \in V)\)
を設定しています。
15~17行目では3つ目の制約条件(MTZ制約)
\(y_{i}-y_{j}+|V|x_{ij} \leq |V|-1\)
を設定しています。
21行目で問題を解いています。
24行目で解の状態を表示しています。「Optimal」と表示されたら最適解を求めることができています。
27~31行目で最適解を表示しています。値が1の変数のみ表示するようにしています。
33行目で最適値を表示しています。
結果の解釈

1行目が解の状態、2~7行目は最適解を表しています。8行目が最適値を表しています。1行目を見ると「Optimal」と表示されているのでちゃんと最適解が得られていることが分かります。
最適解を見ると、
0(東京)→1(ニューヨーク)→2(ブエノスアイレス)
→4(ロンドン)→5(カイロ)→3(ソウル)→0(東京)
というルートが最も移動距離の合計が短い旅行ルートということが分かりました。
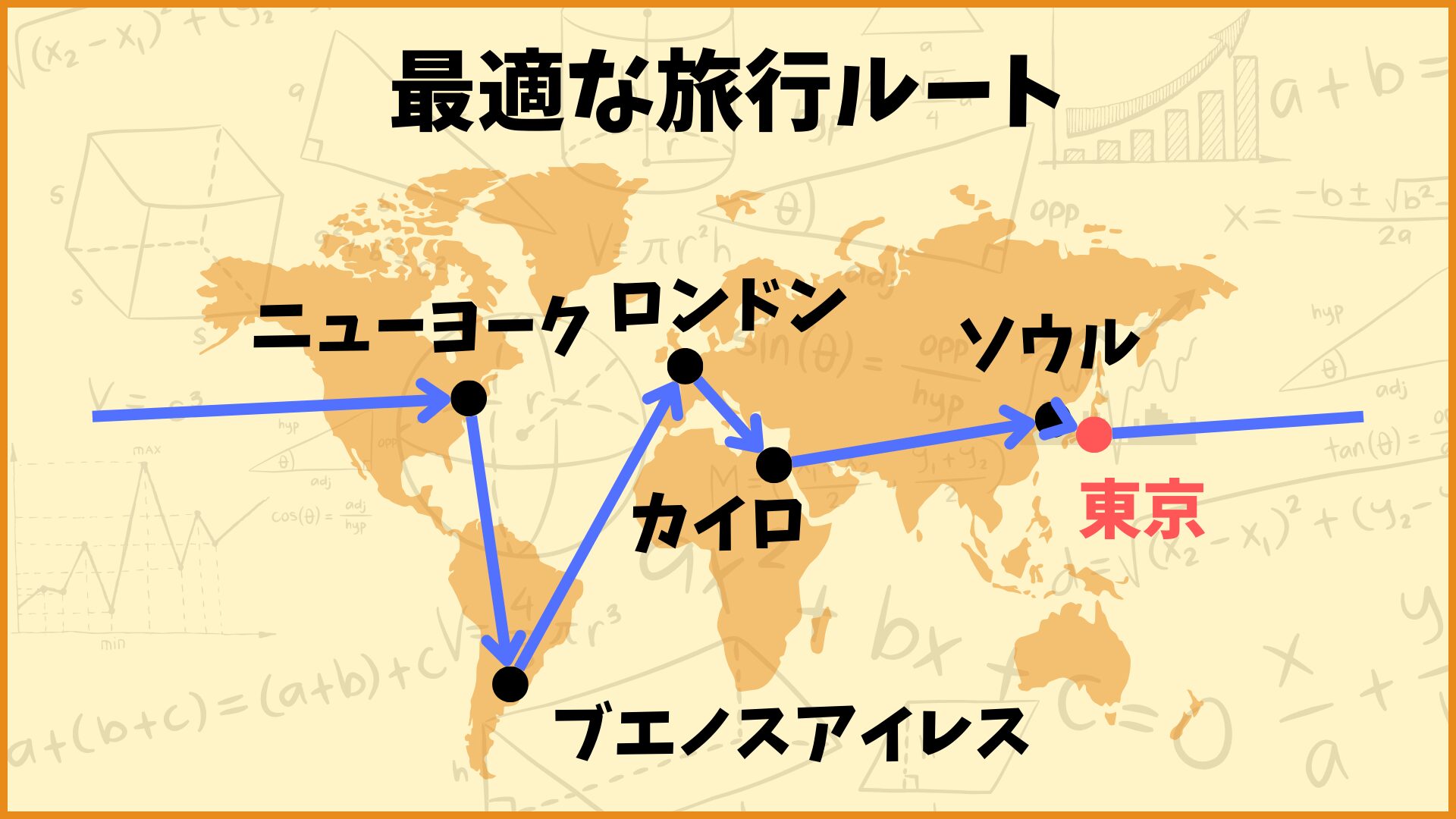
最適値を見ると43703と表示されていますが、これはこの世界一周旅行では43703km移動するということを表しています。
おわりに
いかがでしたか。
今回の記事ではMTZ制約について解説していきました。
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
参考文献
Kulkarni, R. V., and Pramod R. Bhave. “Integer programming formulations of vehicle routing problems.” European journal of operational research 20.1 (1985): 58-67.




