- ORがどんな学問かが分かる
- 世の中でORが使われている例が分かる
こんにちは!しゅんです!
今回の記事では世の中のどんなところにオペレーションズ・リサーチが使われているかを紹介していきます!
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
オペレーションズ・リサーチってなに?
まず最初にオペレーションズ・リサーチ(OR)がどんな学問なのかを説明します。一言で説明すると
「数式を使って世の中に存在する問題を解決する学問」
です。

例えば駅Aから電車で駅Gまで行きたいときに、どのようなルートで行けば最短で着くのかという問題はORの手法で解くことができるんです。
高校で勉強する数学の中に線形計画法というものがありますが、線形計画法はORの手法の1つです。
上記の例以外にも世の中で使われているORはたくさんあります。いくつか見ていきましょう!
路線案内アプリ
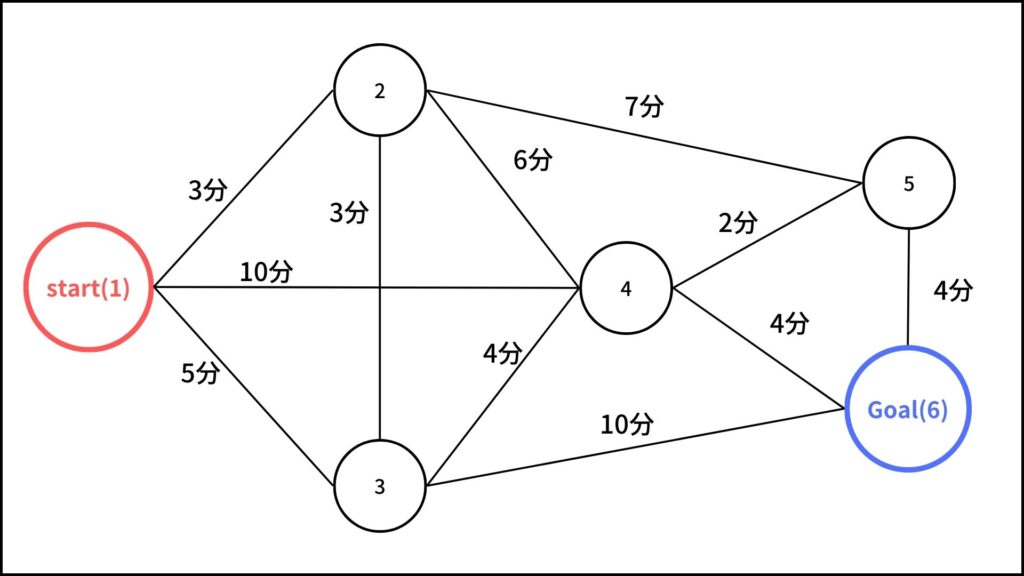
今さっき簡単に紹介しましたが、ある駅から別の駅に行くときに、路線案内アプリを使って最短ルートを検索したりしますよね。これはORの手法を使えば最短ルートを計算できるんです。
この図のようにある駅から別の駅に行くまでに必要な時間はデータとしてあるので、それを用いて最短時間を求めます。
ある駅から別の駅までの最短ルートを求める問題は、ORの最短経路問題という問題に分類されます。この問題の解き方は色々ありますが、その中でもダイクストラ法が一番有名な解法だと思います。
ダイクストラ法を簡単に説明するとスタート地点から近い順に各地点に行く最短経路を逐一求めてGoalまで求める方法です。
例えば上の図で説明すると駅1~駅2間の最短経路の時間は3分で、駅1~駅3間の最短経路の時間は5分であることはすぐにわかります。
そして駅1~駅4間の最短経路は2を通るか3を通るか直接行くかの3パターンになります。その中で最短時間になるのは駅1~駅2~駅4の経路か駅1~駅3~駅4の経路で、この経路で行けば駅4まで9分でたどり着くことができます。
これを繰り返すことによって駅1~駅6までの最短経路を求めることができます。
もっと知りたい場合は「最短経路問題」や「ダイクストラ法」で検索すると詳しく説明されているサイトが見つかると思います!ぼくも別の記事で解説しているのでぜひ見てみてください!
例えば時間のデータの代わりに値段のデータを使えば最小金額で行くルートも求めることができますね。上の例は一番単純な例で、実際は乗換時の待ち時間などを考慮する必要があり、もっと難しい問題を解くことになります。
アルバイトのシフト作成

実はバイトのシフトもORで作成することができます!
各曜日に必要な人数、バイトの従業員の人数、従業員の出勤希望日といったデータがあればどの曜日にどの従業員が出勤するかを計算することができます。
例えば4連勤を禁止する制約を追加したり、必ず男女1人ずつはシフトに入る制約を追加したり、必ずバイトリーダーが入る制約を追加したり、いろいろ制約条件を追加することもできます。
もっと知りたい方は「シフト作成 オペレーションズリサーチ」や「シフト作成 整数計画問題」などで検索すると、詳しい説明をしているサイトが見つかると思います!ぼくも別の記事で解説しているのでぜひ見てみてください!
スポーツチームの強さの算定
あるスポーツにおいて、スタッツがデータとしてあればそれを基にした選手やチームの強さを数値化することができたりします。
例えばバスケットボールでいうと、3P成功数、シュート成功数やブロック成功数、出場時間といったスタッツの情報があればそれらを基に強さ(効率値)を求めることができるんです。
入力値を3P成功率の代わりにアシスト数に変更すればまた別の評価軸での強さを算定することもできます。
さらに言うと同じ強さの選手でも、この選手は3P成功数が強みだとか、シュート成功数が強みだとかを知ることもできます。
ここでは詳しいアルゴリズムの解説は難しいので行いませんが、もし具体的にどうやって解くのか知りたい方は「DEA法」や「データ包絡分析法」で調べてみてください!
例えば仮に強さを算定して理想のチームができたとして、それが本当に最強のチームかどうかはどうやって調べるのでしょうか。
実はそれもORで出来てしまいます。1回のオフェンスとディフェンスの中でシュートを決める確率がどれくらいなのかなどが分かれば5回目のシュートが入る確率などが求められるので、それらを組み合わせて最終的に勝利する確率が求められたりします。
更に詳しく知りたい方は「マルコフモデル」や「マルコフ連鎖」で調べてみてください!
物流の配送ルートを決定する
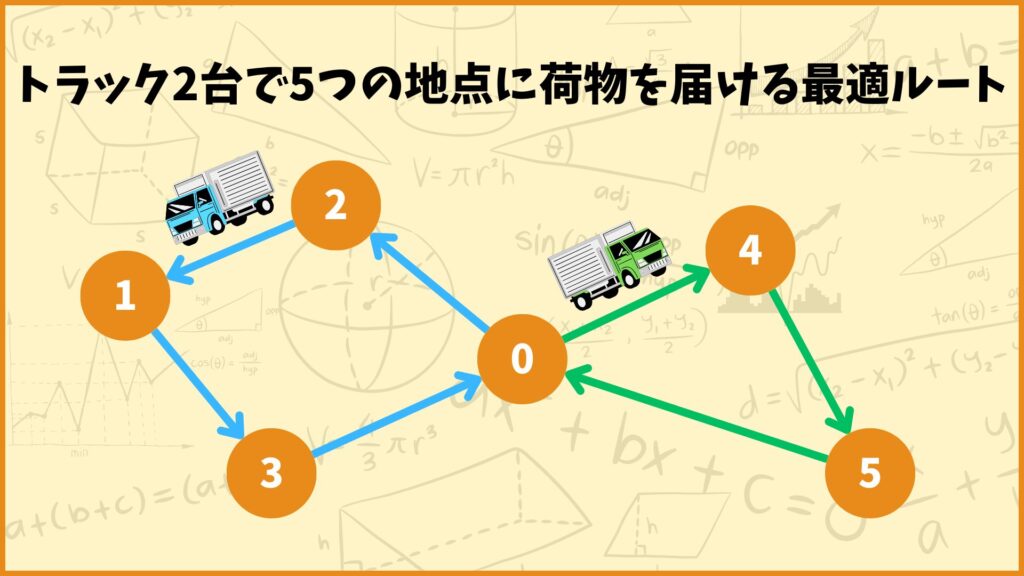
トラックで荷物を配送するときに、どんなルートで配送すれば良いかを計算するのもORを使って解決できます。
例えば地点0を出発地点として2台のトラックで5つの地点に荷物を届けるときに、トラックの移動距離の合計が最小となるような配送ルートを求める問題はよくあるORの問題の1つです。
このような問題は配送計画問題やVRP(Vehicle Routing Problem)と呼ばれます。もっと知りたい方は「配送計画問題」や「VRP」などで検索すると、詳しい説明をしているサイトが見つかると思います!ぼくも別の記事で解説しているのでぜひ見てみてください!
数独を解く

実はORを使って数独を解くことができちゃいます。数独は縦、横、太線で区切られた3×3のブロックに1から9の数字を1つずつ入れていくゲームですが、このことを数式で表すことで解くことができます。
もっと知りたい方は「数独 組合せ最適化」や「数独 整数計画問題」で検索すると詳しく説明しているサイトが出てくると思います。ぼくも別の記事で解説しているのでぜひ見てみてください!
おわりに
いかがでしたでしょうか。今回紹介したものはごく一部で、実際にはもっといろんなところでORが使われています。
今までたくさんORの話をしておいてあれですが、注意しておきたいのは仮に答えが出たとしてもあくまでそれは完璧ではないということです。
実際にORを使って出た答えと現実問題を比較してみると意外と実現不可能な答えになっていることはよくあります。
現実問題を100%数式再現するのは難しいし、仮に再現できたとしてもそれを計算し終わるのに莫大な時間がかかってしまってはあまり意味はありません。
ORを使って出た答えを鵜呑みにするのではなく、現実問題と照らし合わせて修正すべき箇所がないか検討することが重要です。
とはいえORで出た答えは現実問題を検討するうえで参考になるのでやはり非常に便利だと思っています。
最後までこの記事を読んでくれてありがとうございました!
この記事が役に立ったら幸いです。











