こんにちは!しゅんです!
いきなりですが皆さんはいまからポスティングをしようと思っています。
ポスティングを簡単に説明すると家のポストにチラシを配ることです。仕事はなるべく早く終わらせたいので、できれば最短のルートでチラシを配りたいですよね。
この記事では移動距離が最小となるようなポスティングの経路を、数学を使って求めてみたいと思います!
組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
問題設定
それではまず最初に今回考えたい問題をちゃんと設定しましょう
問題設定
・ポスティングを2人で行い、2人で合計2000枚のチラシを配りたい。
・1人当たり最大1200枚までチラシを持てる。
・合計で5つのマンションにチラシを配ることを考える。
・ポスティングは拠点をスタート地点とし、いくつかのマンションを経由して拠点に戻ってくるルートを考える。
・各マンションは1度しか訪れない。(複数の人が同じマンションにポスティングすることはない。)
・各マンションには、何枚チラシを配れるかの見込みがあり、以下の通りである。
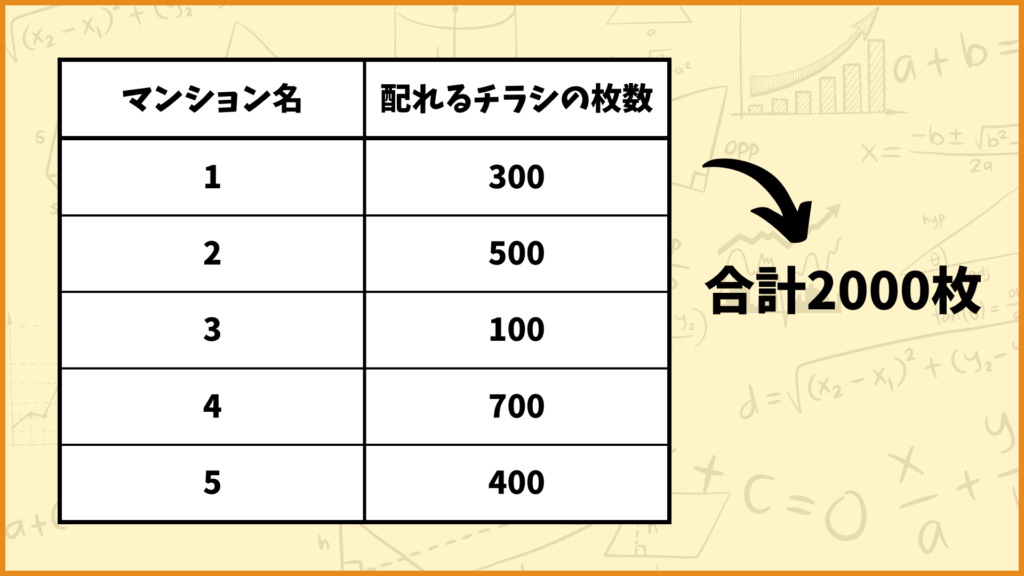
・各マンションの位置関係は以下の通りである。(なお0は拠点とする)
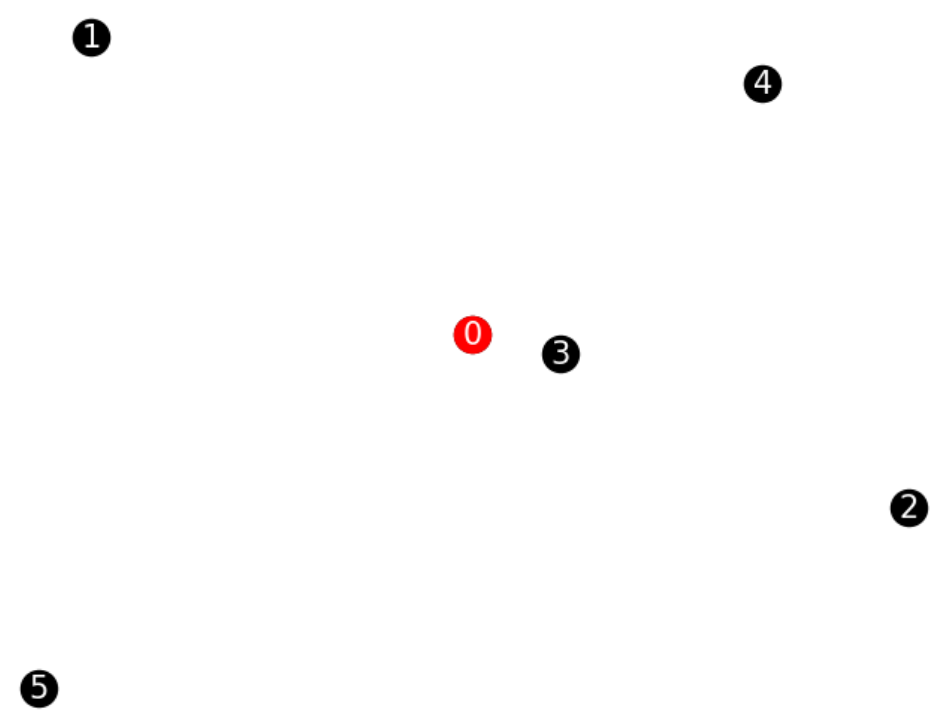
目的
2人の移動距離の合計が最小となるようなポスティングのルートを求めたい。
要は以下のようなルートを考える訳です。
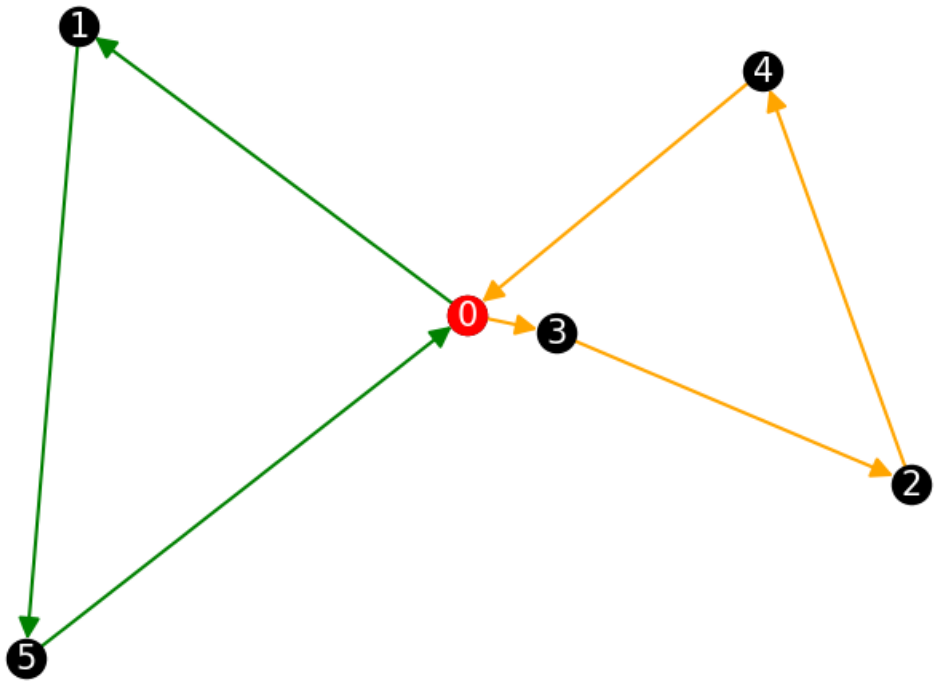
拠点からスタートして、それぞれ緑のルートとオレンジのルートでチラシを配ってまた拠点に帰ってきます。それでは実際に求めてみましょう。
ちなみにこのルートはNGなルートの例です。オレンジのルートではマンション2,3,4にチラシを配ることになっていますが、そうすると合計1300枚のチラシを配ることになります。
ところが1人当たり最大で1200枚までしかチラシを持てないのでこのルートはダメなルートとなります。
整数計画問題として定式化
「記号の設定」、「目的関数の設定」、「制約条件の設定」の3つに分けて説明したいと思います。
記号の設定
パラメータとして地点の集合と、チラシを配る人の集合、各地点で配るチラシの枚数、1人が持てるチラシの枚数の最大値、各地点間の距離を設定します。変数は0-1変数\(x_{iuv}\)を使いたいと思います。
パラメータ:
\(V\) : 地点の集合
\(T\) : チラシを配る人の集合
\(p_u\) : 地点\(u\)で配るチラシの枚数
\(P\) : 1人が持てるチラシの枚数の最大値
\(d_{uv}\) : 地点\(u\)と地点\(v\)間の距離
変数:
\(x_{iuv} \in \{0,1\}\) : 人\(i\)が地点\(u\)から地点\(v\)に向かうなら1、そうでないなら0を取る0-1変数
より一般的な議論をするために全て文字で表しています。今回の問題だけで言えば
\(V = \{0,1,2,3,4,5\}\)(0は拠点を表す)
\(T = \{1,2\}\)
\(p_1 = 300, p_2 = 500, p_3 = 100, p_3 = 700, p_5 = 400\)
\(P = 1200\)
また各地点は\([0,10] \times [0,10]\)の2次元ユークリッド平面上に配置し、\(d_{uv}\)はユークリッド距離、すなわち
\(d_{uv} = \sqrt{(x_u – x_v)^2 + (y_u – y_v)^2}\)
で定義します。(\((x_u,y_u)\)は地点\(u\)のx座標とy座標を表しています。)
目的関数の設定
この問題の目的は
「2人の移動距離の合計が最小となるようなルートを求めたい」
です。よって以下のように表すことができます。
目的関数:
\(\sum\limits_{i \in T}\sum\limits_{u \in V}\sum\limits_{v \in V , u \ne v} d_{uv}x_{iuv} \)
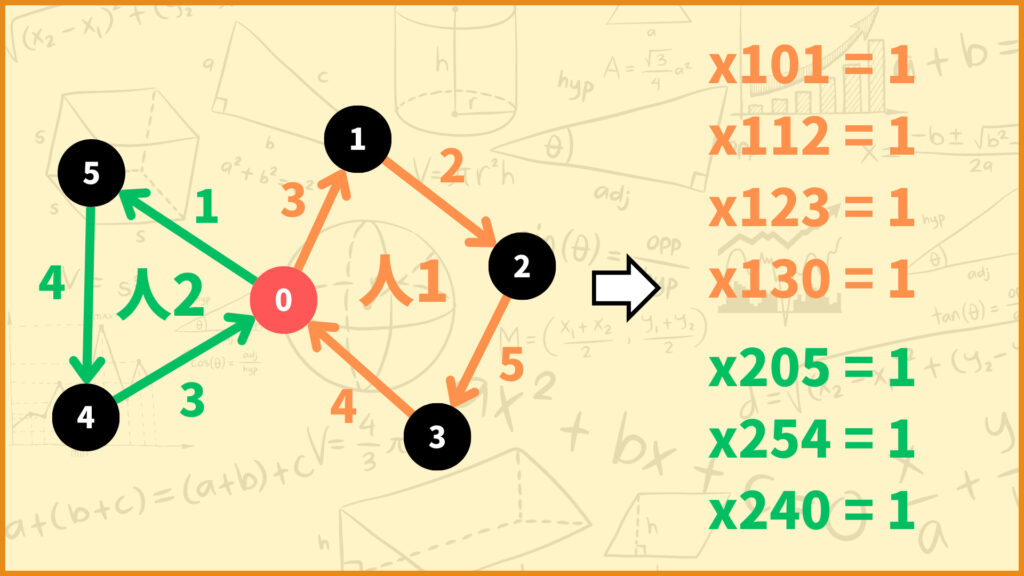
例えば人1が0→1→2→3→0のルート、人2が0→5→4→0のルートでチラシを配るとします。このとき変数の値は
\(x_{101} = x_{112} = x_{123} = x_{130} = x_{205} = x_{254} = x_{240} = 1\)
で他の変数の値は0となります。また、目的関数値は
\(\sum\limits_{i = T}\sum\limits_{u \in V}\sum\limits_{v \in V, u \ne v} x_{ijk}\)
\( = 3 x_{101} + 2x_{112} + 5x_{123} + 4x_{130} + x_{205} + 4x_{254} + 3x_{240}\)
\( = 22\)
となります。この値は2人の移動距離の合計と対応します。今回はこれを最小化することを考えます。
3つ目の\(\sum\)の所が\(u \ne v\)となっているのは自己ループを防ぐためです。仮に\(x_{122} = 1\)とすると人1が地点2から地点2に向かうということになってしまいます。
この後の「pythonで解いてみる」の所でも説明しますが、そもそも変数を作る段階で\(x_{iuu} \; (\forall u \in V)\)は作らないので\(u \ne v\)としないとエラーが出てしまいます。
今後登場する\(u \ne v\)はすべて同じ理由です。
\( \min \;\;\; \sum\limits_{i \in T}\sum\limits_{u \in V}\sum\limits_{v \in V, u \ne v} d_{uv}x_{iuv} \)
制約条件の設定
制約条件:
\(\sum\limits_{i \in T}\sum\limits_{v \in V, u \ne v}x_{iuv} = 1 \;\;\; (\forall u \in V \backslash \{0\})\) → ①
\(\sum\limits_{v \in V\backslash \{0\}}x_{i0v}=1 \;\;\; (\forall i \in T)\) → ②
\(\sum\limits_{u \in V, u \ne v}x_{iuv} – \sum\limits_{w \in V, v \ne w}x_{ivw} =0 \;\;\; (\forall i \in T, \forall v \in V)\) → ③
\( \sum\limits_{u \in V}\sum\limits_{v \in V\backslash\{0\}, u \ne v}p_vx_{iuv} \leq P \;\;\; (\forall i \in T)\) → ④
\(\sum\limits_{i \in T}\sum\limits_{u \in S}\sum\limits_{v \in S, u \ne v}x_{iuv} \leq |S| -1 \;\;\; (\forall S \subseteq V\backslash\{0\}, |S| \geq 2)\) → ⑤
1つずつ解説していきます。
1つ目の制約
1つ目の制約:
\(\sum\limits_{i \in T}\sum\limits_{v \in V, u \ne v}x_{iuv} = 1 \;\;\; (\forall u \in V \backslash\{0\})\)
1つ目の制約はどの地点にも必ず1回だけ配達しに行くということを表しています。

例えば地点3について考えてみましょう。制約式の左辺は
\(\sum\limits_{i \in T}\sum\limits_{v \in V, v \ne 3}x_{i3v}\)
\( = x_{130} + x_{131} + x_{132} + x_{134} + x_{135}\)
\( + x_{230} + x_{231} + x_{232} + x_{234} + x_{235}\)
となります。変数\(x_{iuv}\)は0か1しか取らないので、制約式が成り立つためには上記の10個の変数のうちどれか1つだけが1を取ることを表します。
例えば\(x_{134} = 1\)としましょう。これは
「人1が地点3から地点4に向かう」
ということを表しています。つまり人1が地点3にチラシを配ることができますね。
\((\forall u \in V /\{0\})\)は「地点0(拠点)以外の全ての地点に対して」ということを表します。例えば人1が拠点から地点1に、人2が拠点から地点3に向かう場合\(x_{101} = x_{203} = 1\)となります。
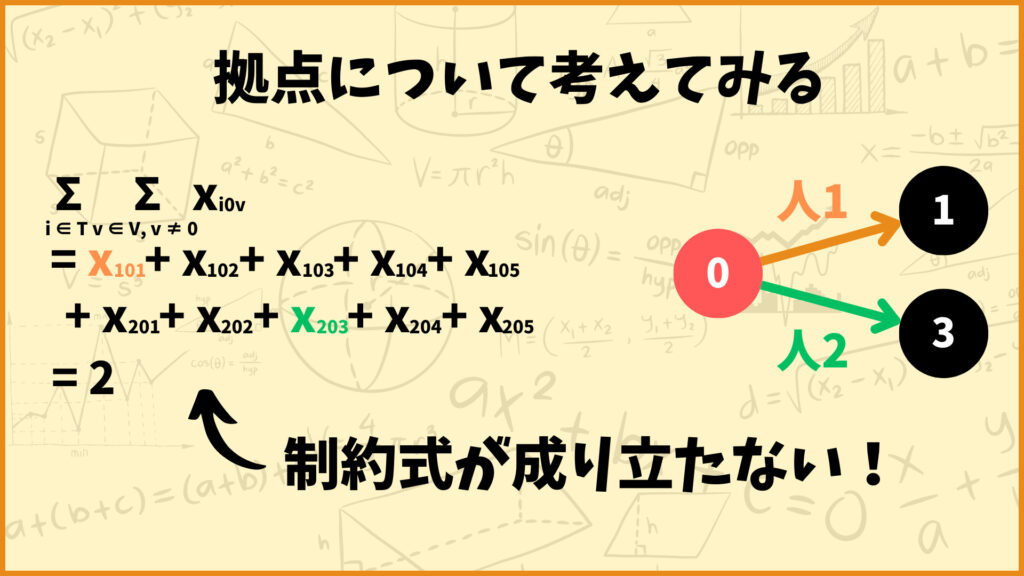
つまり左辺の値が2になるので等式が成り立ちません。そのため\((\forall u \in V /\{0\})\)として拠点を除いているわけです。
2つ目の制約
2つ目の制約:
\(\sum\limits_{v \in V\backslash\{0\}}x_{i0v}=1 \;\;\; (\forall i \in T)\)
2つ目の制約はチラシを配る人が拠点から出発するということを表しています。
例えば人1について考えて見ましょう。左辺は
\(x_{101} + x_{102} + x_{103} + x_{104} + x_{105}\)
となります。これが1を取るので、上記の5つの変数のいずれか1つが1を取ります。例えば\(x_{102}=1\)としましょう。これは
「人1が拠点から地点2に向かう」
ということを表します。
3つ目の制約
3つ目の制約:
\(\sum\limits_{u \in V, u \ne v}x_{iuv} – \sum\limits_{w \in V, v \ne w}x_{ivw} =0 \;\;\; (\forall i \in T, \forall v \in V)\)
3つ目の制約はその地点に向かう回数とその地点から出ていく回数が一致することを表しています。
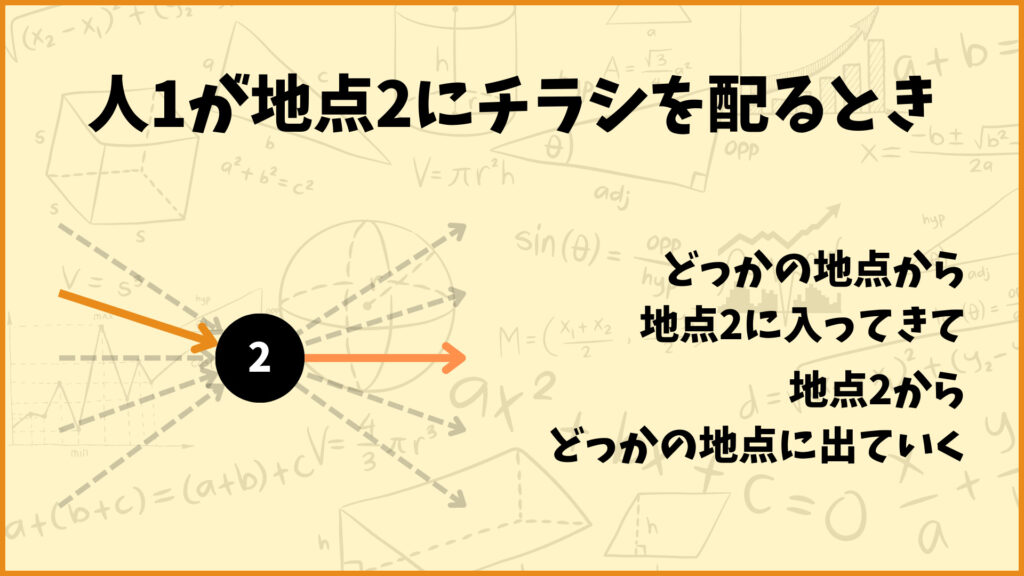
例えば人1が地点2にチラシを配るときを考えましょう。このときは地点2に向かうためにどっか他の地点から地点2に向かいます。そのため
\(\sum\limits_{u \in V, u \ne 2}x_{1u2} = 1\)
となります。また地点2にチラシを配り終わったらどっか他の地点に向かいます。そのため
\(\sum\limits_{w \in V, w \ne 2}x_{12w} = 1\)
となります。したがって
\(\sum\limits_{u \in V, u \ne v}x_{1u2} – \sum\limits_{w \in V, w \ne 2}x_{12w} = 0\)
が成立します。逆にこのとき人2は地点2にチラシを配らないですね。そのため同じように考えると
\(\sum\limits_{u \in V, u \ne 2}x_{2u2} = 0, \;\; \sum\limits_{w \in V, w \ne 2}x_{22w} = 0\)
となり
\(\sum\limits_{u \in V, u \ne 2}x_{2u2} – \sum\limits_{w \in V, w \ne 2}x_{22w} = 0\)
が成り立ちます。
4つ目の制約
4つ目の制約:
\( \sum\limits_{u \in V}\sum\limits_{v \in V\backslash\{0\}, u \ne v}p_vx_{iuv} \leq P \;\;\; (\forall i \in T)\)
4つ目の制約はチラシの重量制限を満たすということを表しています。
例えば人1が地点0(拠点)→地点1→地点3→地点4→地点0(拠点)というルートでチラシを配るとします。
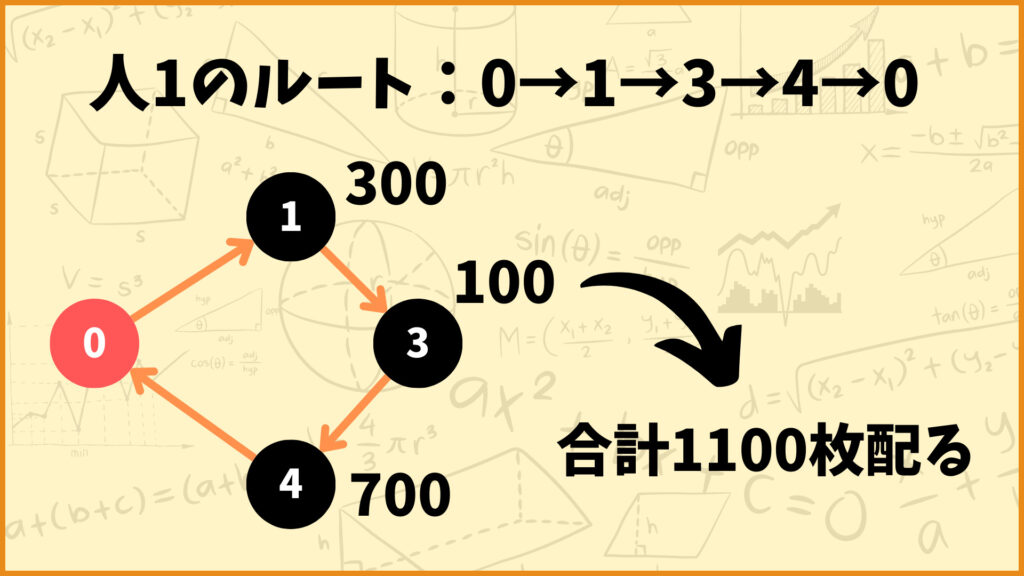
このとき\(x_{101} = x_{113} = x_{134} = x_{140} = 1\)となります。また左辺の値は
\(\sum\limits_{\forall u \in V}\sum\limits_{v \in V\backslash\{0\}, u \ne v}p_vx_{1uv}\)
\(=p_1x_{101} + p_3x_{113} + p_4x_{134}=300 + 100 + 700=1100\)
となります。これは人1が配るチラシの枚数の合計と対応します。1人当たり最大で\(P\)枚までチラシを持てるのでこの左辺の式が\(P\)以下になれば良いですね。(今回の場合だと\(P=1200\)です。)
5つ目の制約
5つ目の制約:
\(\sum\limits_{i \in T}\sum\limits_{u \in S}\sum\limits_{v \in S, u \in v}x_{iuv} \leq |S| – 1 \;\;\; (\forall S \subseteq V\backslash\{0\}, |S| \geq 2)\)
5つ目の制約は部分巡回路除去制約です。
この制約は第4節の所で詳しく説明しています。
整数計画問題としてまとめる
以上のことを踏まえて整数計画問題として定式化しましょう。
パラメータ:
\(V\) : 地点の集合
\(T\) : チラシを配る人の集合
\(p_u\) : 地点\(u\)で配るチラシの枚数
\(P\) : 1人が持てるチラシの枚数の最大値
\(d_{uv}\) : 地点\(u\)と地点\(v\)間の距離
変数:
\(x_{iuv} \in \{0,1\}\) : 人\(i\)が地点\(u\)から地点\(v\)に向かうなら1、そうでないなら0を取る0-1変数
定式化:
\( \min \;\;\; \sum\limits_{i \in T}\sum\limits_{u \in V}\sum\limits_{v \in V, u \ne v} d_{uv}x_{iuv} \)
\(\;\text{s.t.}\;\;\;\sum\limits_{i \in T}\sum\limits_{v \in V, u \ne v}x_{iuv} = 1 \;\;\; (\forall u \in V \backslash\{0\})\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{v \in V\backslash\{0\}}x_{i0v}=1 \;\;\; (\forall i \in T)\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{u \in V, u \ne v}x_{iuv} – \sum\limits_{w \in V, v \ne w}x_{ivw} =0 \;\;\; (\forall i \in T, \forall v \in V)\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{u \in V}\sum\limits_{v \in V\backslash\{0\}, u \ne v}p_vx_{iuv} \leq P \;\;\; (\forall i \in T)\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in T}\sum\limits_{u \in S}\sum\limits_{v \in S, u \ne v}x_{iuv} \leq |S| -1 \;\;\; (\forall S \subseteq V\backslash\{0\}, |S| \geq 2)\)
\(\;\;\;\;\;\;\;\;\; x_{iuv} \in \{0,1\} \;\;\; (\forall i \in T, \forall u \in V, \forall v \in V, u \ne v)\)
この問題は配送計画問題(vehicle routing problem)としてみなすことができます。
部分巡回路ってなに?
それでは先ほど説明を飛ばした部分巡回路除去制約について説明していきます。今回のようにルートの最適化を考える場合は、部分巡回路というものを考慮する必要があります。
部分巡回路ってなに?
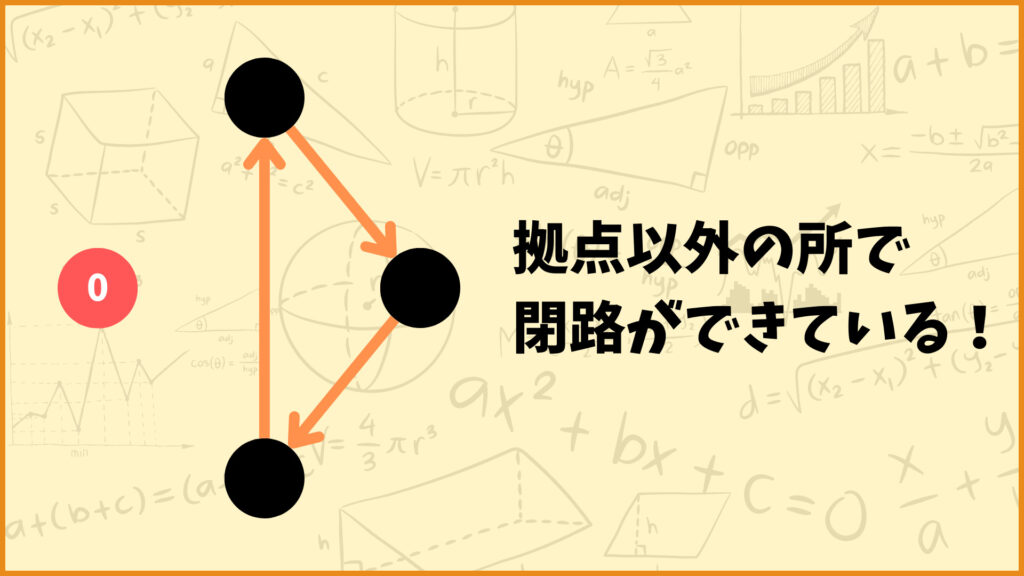
部分巡回路は上図のようなルートです。本来は拠点からスタートして拠点に戻ってくるルートを考えたいのですが、上図は拠点以外の所で閉路ができています。これが部分巡回路です。
ポスティングのルート最適化では部分巡回路はできてほしくないので、除去する必要があります。
どうやって部分巡回路を除去する?
部分巡回路除去制約:
\(\sum\limits_{i \in T}\sum\limits_{u \in S}\sum\limits_{v \in S, u \ne v}x_{iuv} \leq |S| -1 \;\;\; (\forall S \subseteq V/\{0\}, |S| \geq 2)\)
結論上記の制約で部分巡回路を除去することができます。まず記号の説明をします。\(S\)は拠点を除いた地点の集合\(V\backslash\{0\}\)の部分集合です。例えば\(S = \{1,2\}\)とします。部分巡回路を持たないルートと持つルートをそれぞれ考えてみましょう。
部分巡回路を持たない場合
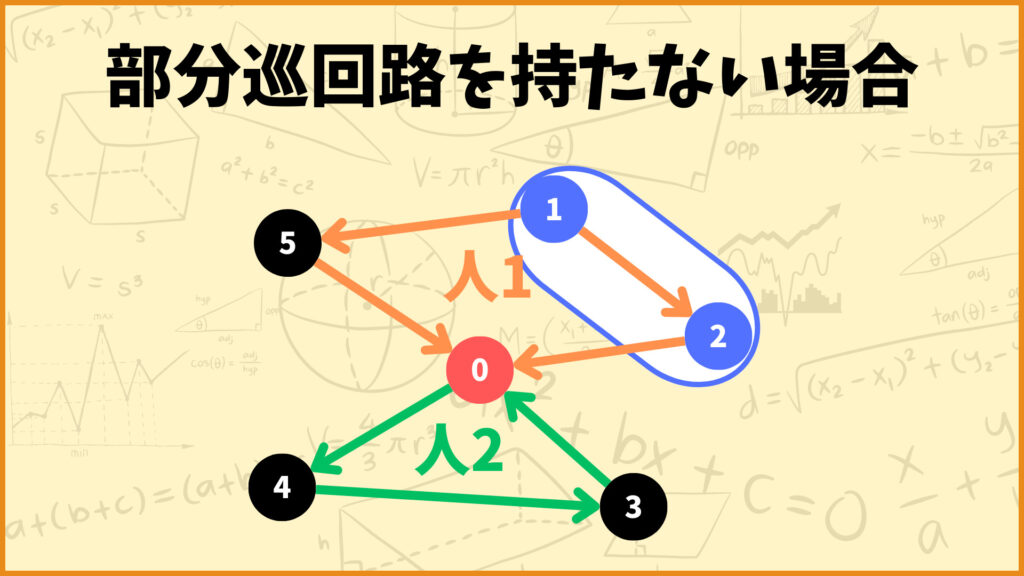
上記のようなルートを考えると、\(x_{112} = 1\)となるので、左辺は
\(\sum\limits_{i \in T}\sum\limits_{u \in S}\sum\limits_{v \in S, u \ne v}x_{iuv}\)
\( = x_{112} + x_{121} + x_{212} + x_{221}\)
\( = x_{112} = 1\)
となり、右辺は
\(|S|-1 = 2 -1 =1\)
となるので制約式を満たします。
部分巡回路を持つ場合
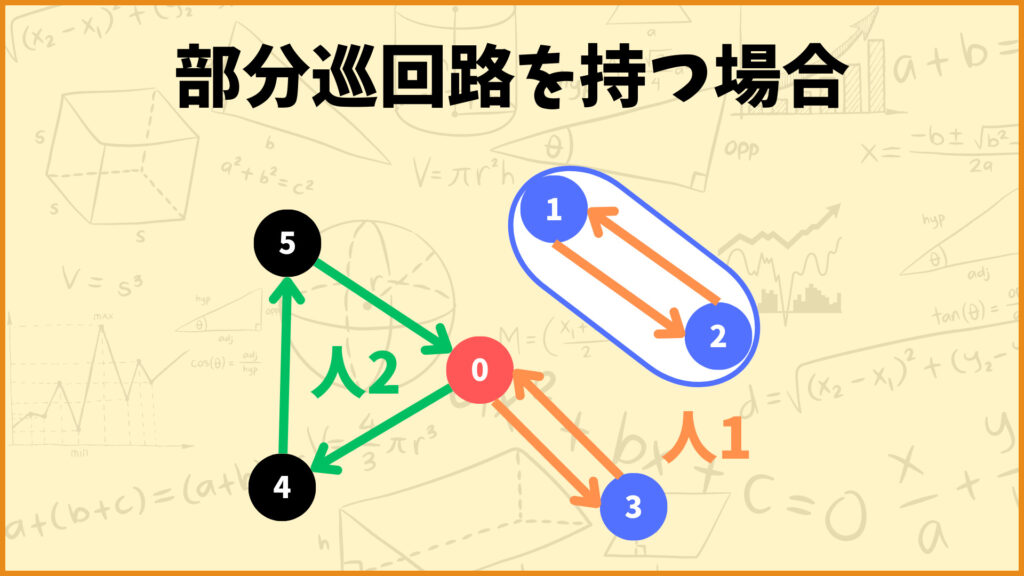
上の例は制約式①~⑤を満たすルートですが部分巡回路を持っています。(地点1と地点2の間が部分巡回路です)
このとき\(x_{112} = x_{121} = 1\)となり、制約式の左辺は
\(\sum\limits_{i \in T}\sum\limits_{u \in S}\sum\limits_{v \in S, u \ne v}x_{iuv}\)
\( = x_{112} + x_{121} + x_{212} + x_{221}\)
\( = x_{112} + x_{121} = 2\)
となり、右辺は
\(|S|-1 = 2 -1 =1\)
となるので制約式を満たしません。
\(|S| \geq 2\)な理由を考えてみましょう。まず\(|S|=0\)は明らかに必要ないですね。次に\(|S|=1\)の場合を考えてみましょう。例えば\(S = \{1\}\)とすると左辺は
\(\sum\limits_{i \in T}\sum\limits_{u \in \{1\}}\sum\limits_{v \in \{1\}, u \ne v}x_{iuv}\)
となります。しかしこれは
\(u = 1,v = 1, u \ne v\)
っていう矛盾した式になってしまいます。そのため\(|S| \geq 2\)となります。
部分巡回路除去制約(DFJ制約)の問題点
今回用いた部分巡回路除去制約はDFJ制約と呼ばれます。この制約の問題点は、
「制約の本数がめっちゃ多い」
ということです。もっとちゃんと言うと、チラシを配る地点の数が増えるにつれて制約の本数が指数的に増加してしまうのがDFJ制約の問題点です。制約の本数を数えてみましょう。
制約式の本数は以下の条件を満たす集合\(S\)の総数と同じになります。
\(S \subseteq V\backslash\{0\}, \; |S| \geq 2.\)
\(V\backslash\{0\}\)の部分集合の総数は\(2^{|V|-1}\)個あります。
要素数が1の\(V\backslash\{0\}\)の部分集合の総数は\(|V|-1\)個あり、それらは上記の条件を満たしません。
\(\emptyset\)は\(V\)の部分集合で、これも上記の条件を満たしません。
以上より条件を満たす集合\(S\)の総数は
\(2^{|V|-1} – |V|\)
となり、これがDFS制約の本数となります。具体的な本数を求めてみると
\(|V| = 6 \Rightarrow 2^5 – 6 = 26\)本
\(|V| = 10 \Rightarrow 2^{9} – 10 = 502\)本
\(|V| = 15 \Rightarrow 2^{14} – 15 = 16369\)本
\(|V| = 20 \Rightarrow 2^{19} – 20 = 524268\)本
制約式の本数が多い分計算時間も長くなってしまいます。今回は\(|V| =6\)なのでそんなに制約式の本数は多くないですが、チラシを配る地点の数が大きくなるとこの定式化では現実的な時間で最適解を求めるのは難しくなります。
pythonで解いてみる
それでは実際にこの問題をpythonで解いてみましょう。結論以下のプログラムを実行することで問題を解くことができます。
## 事前準備
from pulp import *
import random
from itertools import chain, combinations## 記号の設定
random.seed(1)
V = [0,1,2,3,4,5] # 地点の集合V(拠点を含む)
V_0 = [1,2,3,4,5] # 地点の集合V(拠点を含まない)
T = [1,2] # チラシを配る人の集合
p = [300, 500, 100, 700, 400] # 各地点で配るチラシの数
P = 1200 # 1人が持てるチラシの枚数の最大値
# 各地点の座標をランダムに設定
Pos = {}
for v in V_0:
Pos[v] = [random.uniform(0,10), random.uniform(0,10)]
# 地点0の座標を他の地点の平均値に設定
average_x = sum(pos[0] for pos in Pos.values()) / len(Pos)
average_y = sum(pos[1] for pos in Pos.values()) / len(Pos)
Pos[0] = [average_x, average_y]
# # 各地点間の距離を設定
d = {}
for u in V:
for v in V:
d[(u,v)] = ((Pos[u][0] - Pos[v][0])**2 + (Pos[u][1] - Pos[v][1])**2)**(1/2) # ユークリッド距離
# V_0の部分集合Sの集合を返す関数を定義
def powerset(iterable):
s = list(iterable)
return list(map(list, chain.from_iterable(combinations(s, r) for r in range(len(s)+1))))
subsets = powerset(V_0) # V_0の部分集合Sを2次元リスト形式で設定## 整数計画問題として定式化したものを解く
prob = pulp.LpProblem(sense = LpMinimize) # 問題を最小化に設定
x = LpVariable.dicts("x", [(i, u, v) for i in T for u in V for v in V if u != v], cat="Binary") # 0-1変数を設定
prob += lpSum(d[(u,v)] * x[i,u,v] for i in T for u in V for v in V if u != v) # 目的関数を設定
# 制約式1を設定
for v in V_0:
prob += lpSum(x[i,u,v] for i in T for u in V if u != v) == 1
# 制約式2を設定
for i in T:
prob += lpSum(x[i,0,v] for v in V_0) == 1
# 制約式3を設定
for i in T:
for v in V:
prob += lpSum(x[i,u,v] for u in V if u != v) - lpSum(x[i,v,w] for w in V if v != w) == 0
# 制約式4を設定
for i in T:
prob += lpSum(p[v-1] * x[i,u,v] for u in V for v in V_0 if u != v) <= P
# 制約式5を設定
for S in subsets:
if len(S) >= 2:
prob += lpSum(x[i,u,v] for i in T for u in S for v in S if u != v) <= len(S) - 1
# 問題を解く
result = prob.solve()
## 結果の表示
# 解の状態を表示(Optimalと返されたら最適解が得られている)
print(LpStatus[result])
# 最適解の表示(値が1の変数のみ表示)
for i in T:
for u in V:
for v in V:
if u != v:
if x[i,u,v].value() == 1:
print(f"x_{i}_({u},{v}) =", x[i,u,v].value())
# 最適値の表示
print(prob.objective.value())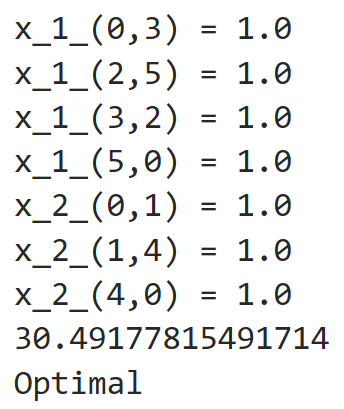
これらのプログラムを実行したら上の結果が得られました。それでは1つずつ説明していきます。
プログラムの説明
事前準備
## 事前準備
from pulp import *
import random
from itertools import chain, combinations
問題を解く前に事前準備をしましょう。pulpはpythonで数理計画問題を解くのに使います。randomは各地点の座標をランダムに設定するときに使います。itertoolsは部分集合\(S\)を作るときに使います。
記号の設定
## 記号の設定
random.seed(1)
V = [0,1,2,3,4,5] # 地点の集合V(拠点を含む)
V_0 = [1,2,3,4,5] # 地点の集合V(拠点を含まない)
T = [1,2] # チラシを配る人の集合
p = [300, 500, 100, 700, 400] # 各地点で配るチラシの数
P = 1200 # 1人が持てるチラシの枚数の最大値
# 各地点の座標をランダムに設定
Pos = {}
for v in V_0:
Pos[v] = [random.uniform(0,10), random.uniform(0,10)]
# 地点0の座標を他の地点の平均値に設定
average_x = sum(pos[0] for pos in Pos.values()) / len(Pos)
average_y = sum(pos[1] for pos in Pos.values()) / len(Pos)
Pos[0] = [average_x, average_y]
# # 各地点間の距離を設定
d = {}
for u in V:
for v in V:
d[(u,v)] = ((Pos[u][0] - Pos[v][0])**2 + (Pos[u][1] - Pos[v][1])**2)**(1/2) # ユークリッド距離
# V_0の冪集合の集合を返す関数を定義
def powerset(iterable):
s = list(iterable)
return list(map(list, chain.from_iterable(combinations(s, r) for r in range(len(s)+1))))
subsets = powerset(V_0) # V_0の冪集合を2次元リスト形式で設定
次に記号の設定の所を説明します。
2行目ではランダム値を固定しています。これを書かないとプログラムを実行するごとに各地点の座標が変わってしまいます。
3~7行目では上から順に「各地点の集合V」、「拠点以外の地点の集合V_0」、「チラシを配る人の集合T」、「各地点で配るチラシの枚数p」、「1人が持てるチラシの枚数の最大値P」を設定しています。
9~16行目では各地点の座標Posを設定しています。座標は辞書形式で設定し、\([0,10] \times [0,10]\)のユークリッド平面上にランダムに配置します。地点0(拠点)の座標は地点1~地点5の座標の平均値にしています。
18~22行目では各地点間の距離dを設定しています。距離はユークリッド距離で計算しています。
24~29行目ではV_0の冪集合を求めています。イメージとしてはV_0の部分集合を全部持ってきたみたいな感じです。
整数計画問題として定式化したものを解く
## 整数計画問題として定式化したものを解く
prob = pulp.LpProblem(sense = LpMinimize) # 問題を最小化に設定
x = LpVariable.dicts("x", [(i, u, v) for i in T for u in V for v in V if u != v], cat="Binary") # 0-1変数を設定
prob += lpSum(d[(u,v)] * x[i,u,v] for i in T for u in V for v in V if u != v) # 目的関数を設定
# 制約式1を設定
for v in V_0:
prob += lpSum(x[i,u,v] for i in T for u in V if u != v) == 1
# 制約式2を設定
for i in T:
prob += lpSum(x[i,0,v] for v in V_0) == 1
# 制約式3を設定
for i in T:
for v in V:
prob += lpSum(x[i,u,v] for u in V if u != v) - lpSum(x[i,v,w] for w in V if v != w) == 0
# 制約式4を設定
for i in T:
prob += lpSum(p[v-1] * x[i,u,v] for u in V for v in V_0 if u != v) <= P
# 制約式5を設定
for S in subsets:
if len(S) >= 2:
prob += lpSum(x[i,u,v] for i in T for u in S for v in S if u != v) <= len(S) - 1
# 問題を解く
result = prob.solve()
## 結果の表示
# 解の状態を表示(Optimalと返されたら最適解が得られている)
print(LpStatus[result])
# 最適解の表示(値が1の変数のみ表示)
for i in T:
for u in V:
for v in V:
if u != v:
if x[i,u,v].value() == 1:
print(f"x_{i}_({u},{v}) =", x[i,u,v].value())
# 最適値の表示
print(prob.objective.value())
2行目で問題を最小化に設定しています。
4行目で0-1変数\(x_{iuv}\)の定義をしています。\(u \ne v\)にしたいのでif u != vとしています。これ以降に出てくるif u != vはすべて同じ意味です。
6行目で目的関数を設定しています。
8~28行目で制約条件を設定しています。
30~31行目で問題を解いています。
36~48行目で結果を表示しています。37行目で解の状態、40~45行目で最適解、48行目で最適値をそれぞれ表示しています。
結果の解釈
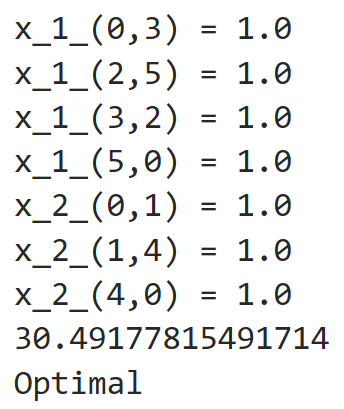
1~7行目は最適解を表しています。8行目が最適値、9行目が解の状態を表しています。Optimalと表示されているのでちゃんと最適解が得られていることが分かります。
最適解を見ると、
人1:0→3→2→5→0
人2:0→1→4→0
というルートが最も距離が短いルートということが分かりました。
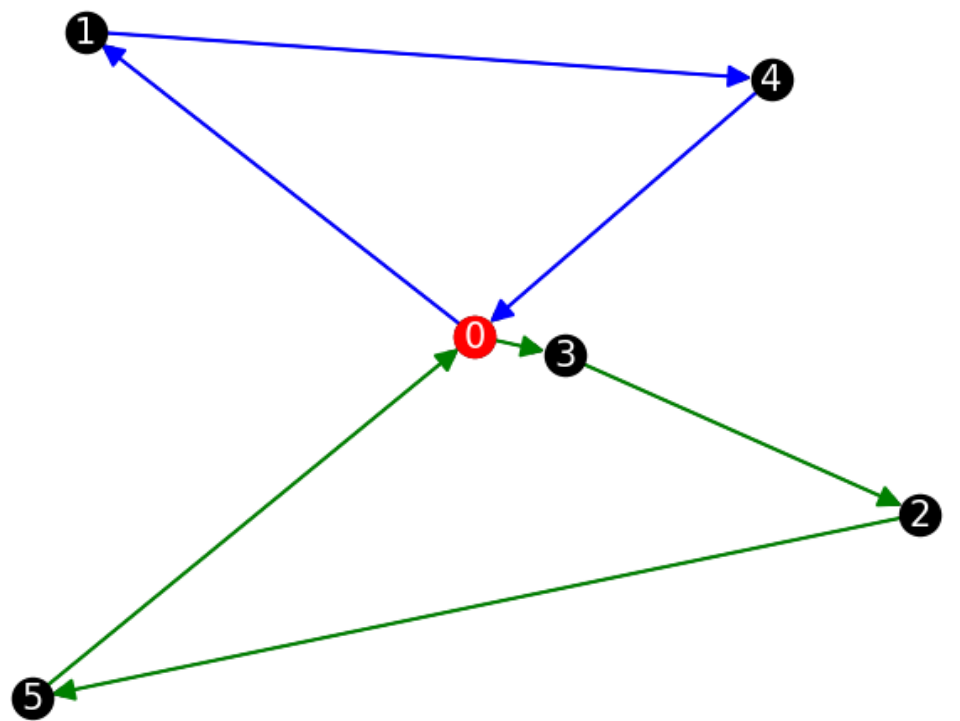
図示したらこんな感じです。
地点数を増やしてみた
遊び感覚ですが、最後に地点数やチラシを配る人数を色々変えて計算してみました。
実行環境:
Python 3.9.1, CPU model: Intel(R) Core(TM) i5-1035G7 CPU @ 1.20GHz, メモリ:16.0 GB、ソルバーはデフォルトのCBCっていうやつです。
\(|V| = 8\)
\(|T| = 3\)
\(p_v \in [100,500]\)
\(P = 1000\)
実行時間:0.673(s)
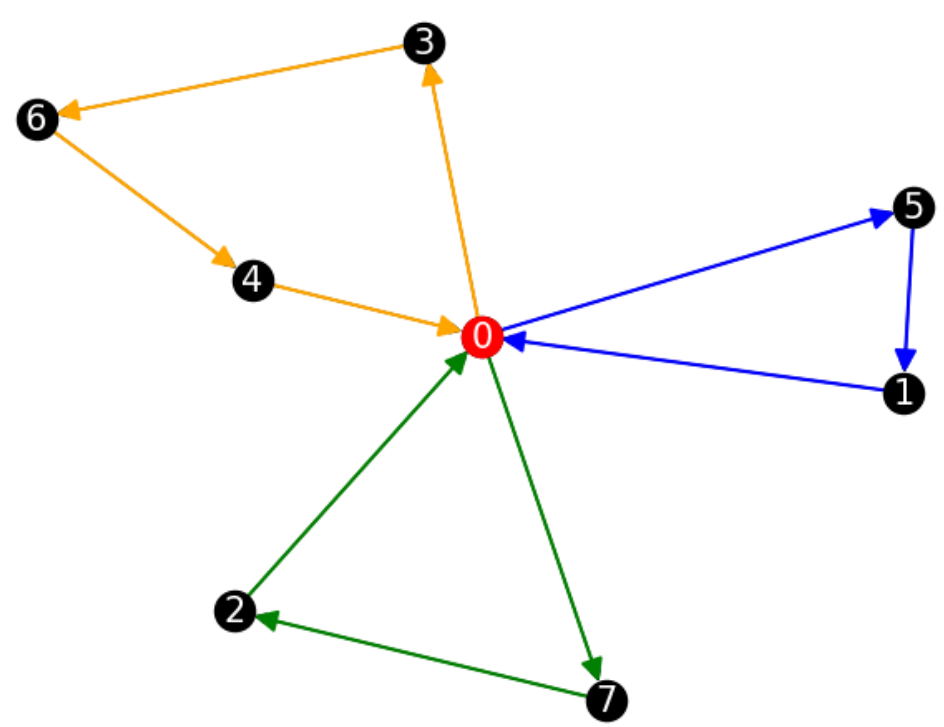
\(|V| = 8\)
\(|T| = 4\)
\(p_v \in [100,500]\)
\(P = 1000\)
実行時間:0.166(s)
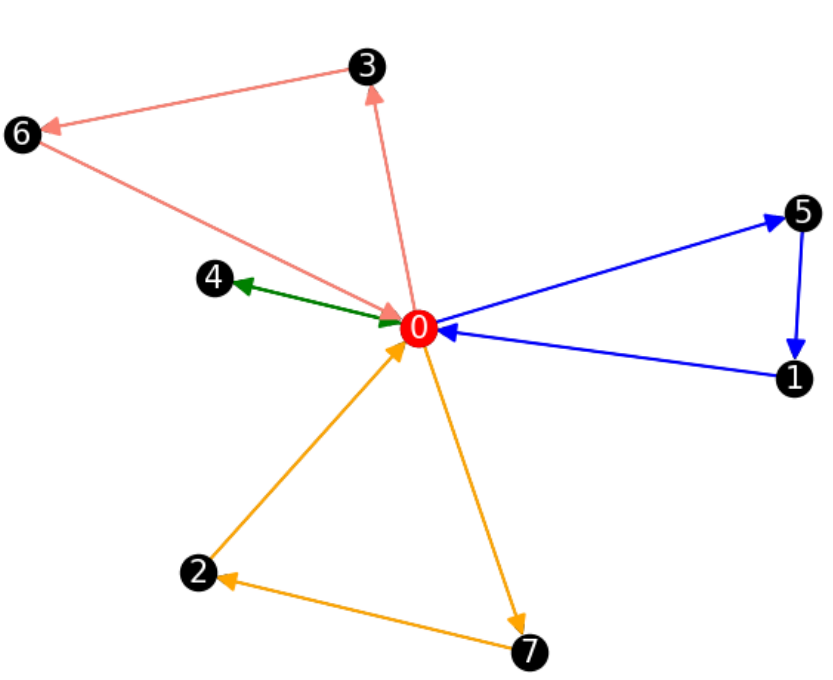
\(|V| = 9\)
\(|T| = 3\)
\(p_v \in [100,500]\)
\(P = 1000\)
実行時間:8.56(s)
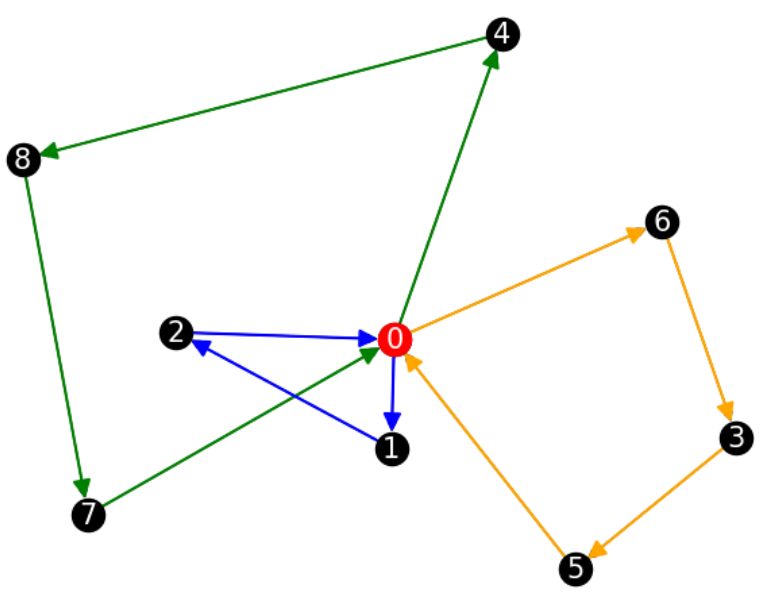
\(|V| = 10\)
\(|T| = 2\)
\(p_v \in [100,500]\)
\(P = 2000\)
実行時間:0.330(s)
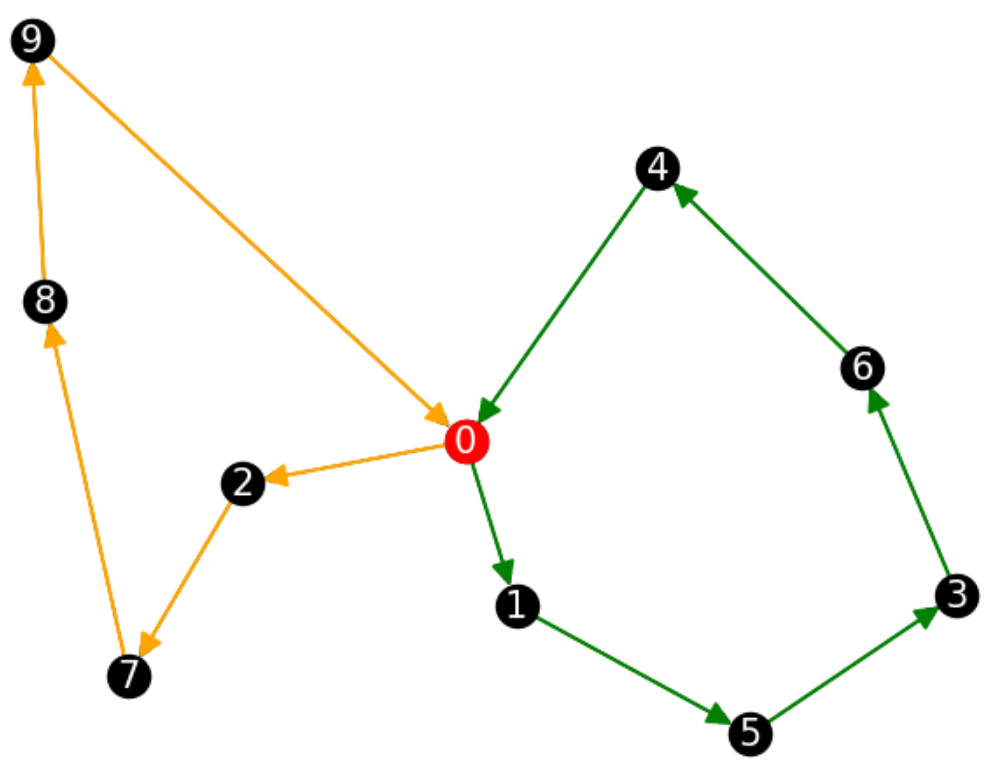
\(|V| = 10\)
\(|T| = 3\)
\(p_v \in [100,500]\)
\(P = 1000\)
実行時間:14.8(s)
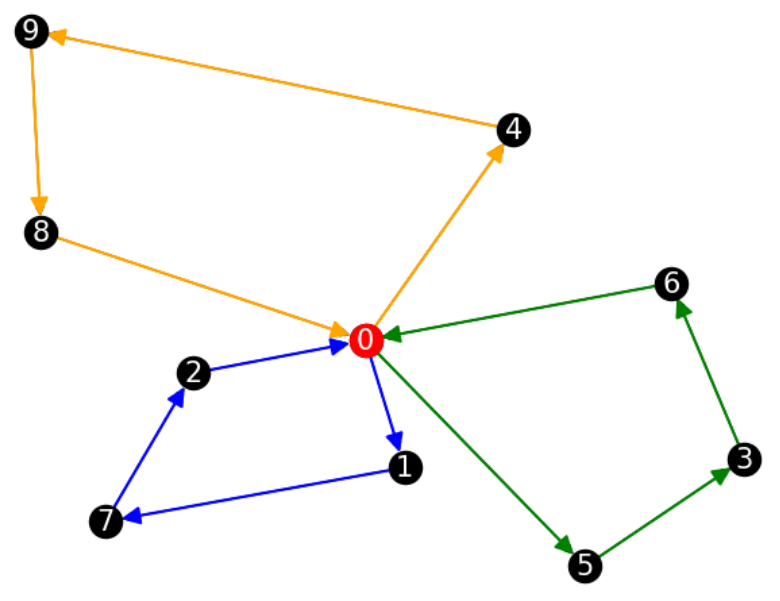
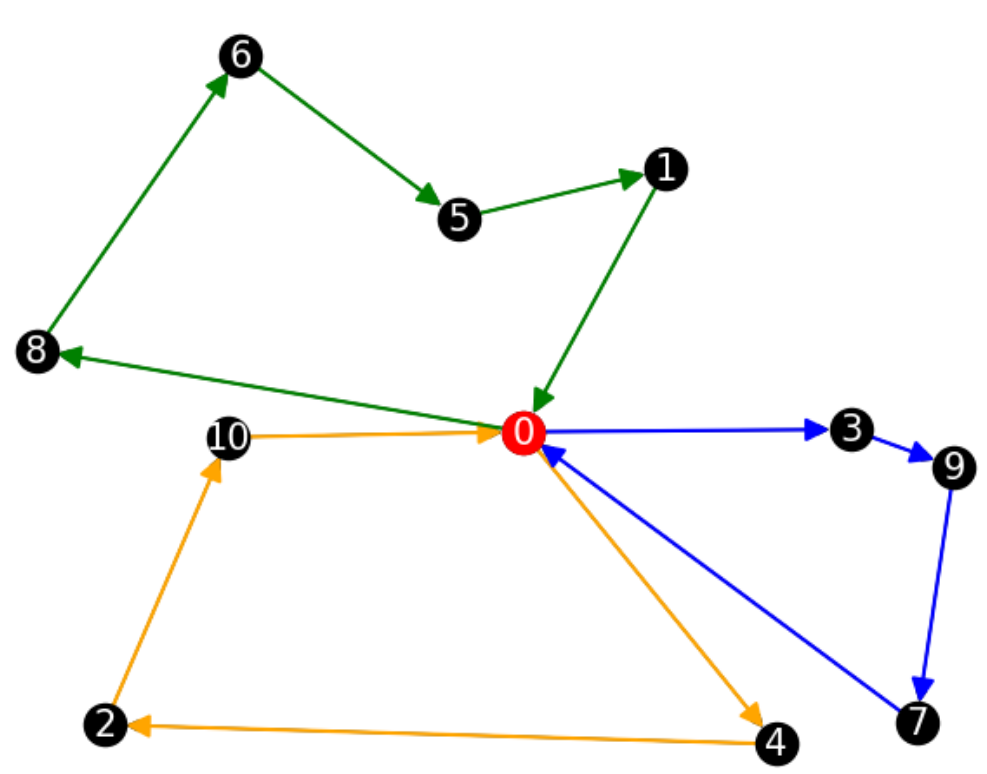
\(|V| = 11\)
\(|T| = 3\)
\(p_v \in [100,500]\)
\(P = 1200\)
実行時間:270(s)
おわりに
いかがでしたか。
今回の記事では数学が世の中で使える例について解説していきました。
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。



