こんにちは!しゅんです!
今回はプリム法について解説していきます!
プリム法はグラフ理論で登場する数学用語です。プリム法はグラフの最小全域木を求めるときに使える便利な手法です。
ということでこの記事ではプリム法がどんな手法なのか、そしてなぜプリム法で最小全域木が求まるのかについて説明していきたいと思います。
それでは解説していきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
プリム法ってなに?
プリム法の簡単な説明
まずはプリム法がどんな手法なのかを説明したいと思います。下のグラフについて考えてみましょう。
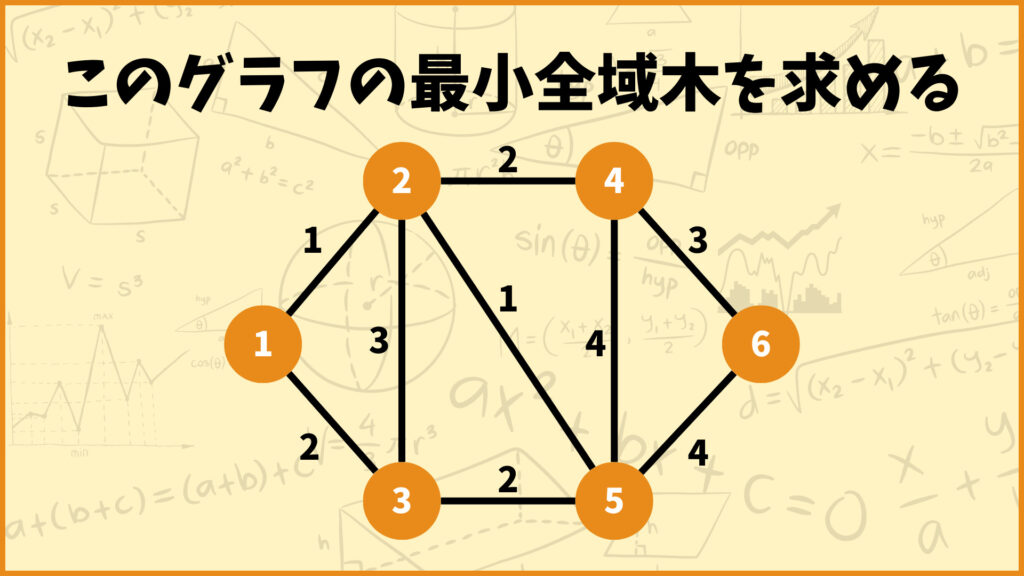
各頂点には1から6までの番号がついており、各辺にはそれぞれ正の重みが付いています。例えば頂点2から頂点3に向かう辺\((2,3)\)の重みは3になります。
このグラフの最小全域木は下のようになります。
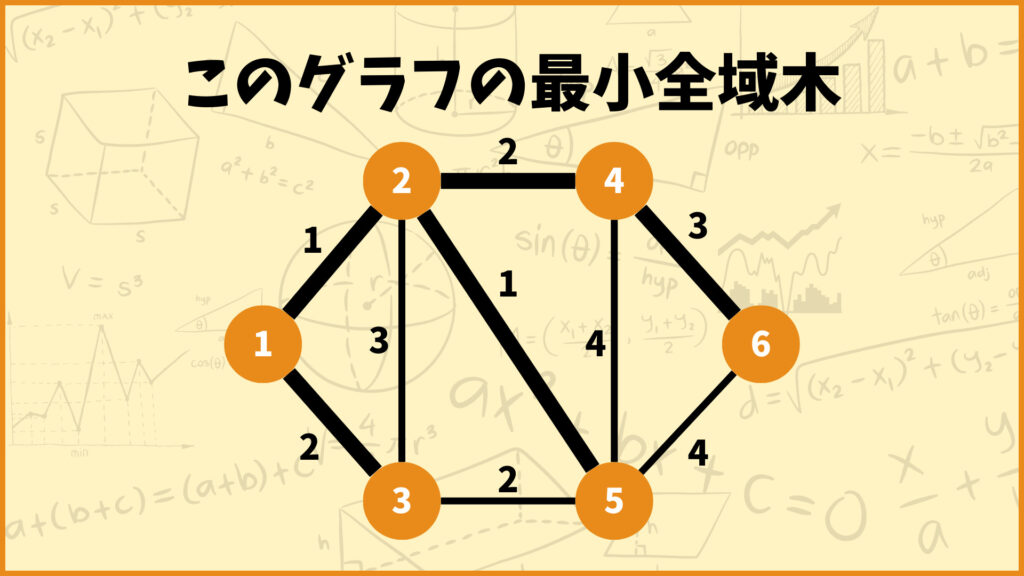
プリム法はこの最小全域木を求める手法の1つです。
プリム法の手順
それでは実際にプリム法の手順を説明していきます。
まず初めに適当にスタートの頂点を決めます。別にどの頂点を選んでもよいですが、今回は頂点1をスタート地点とします。選ばれた頂点は赤色で表し、まだ選ばれてない頂点はオレンジ色で表します。
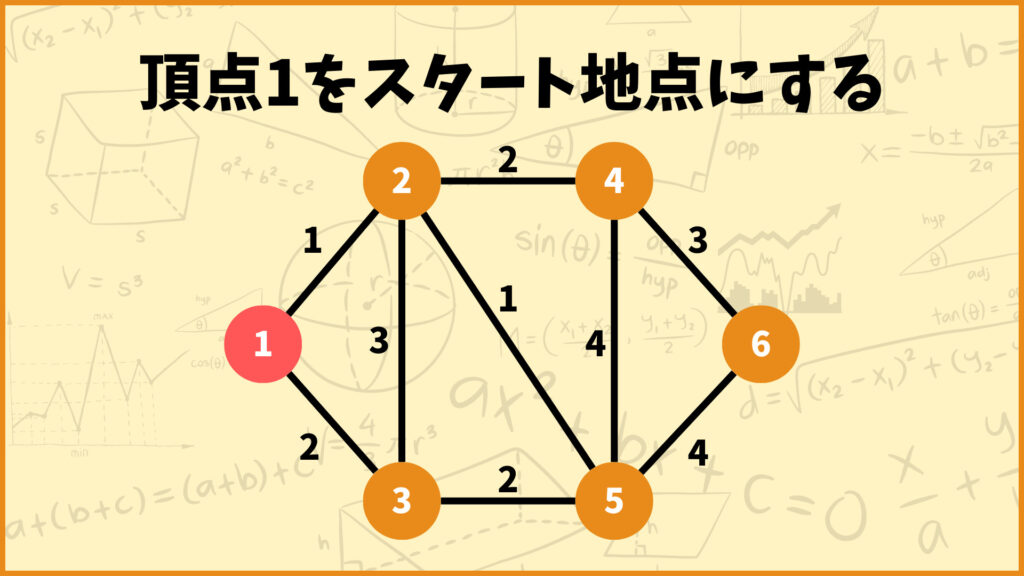
次に頂点1とそれ以外の頂点の間にある辺の中で重みが最も小さい辺を選びます。例えば下の図で言うと頂点1とそれ以外のオレンジ色の頂点の間には辺\((1,2)\)と辺\((1,3)\)の2つの辺があります。
そのうち辺の重みが小さいのは辺\((1,2)\)の方なので、辺\((1,2)\)を選び頂点2を赤色にします。
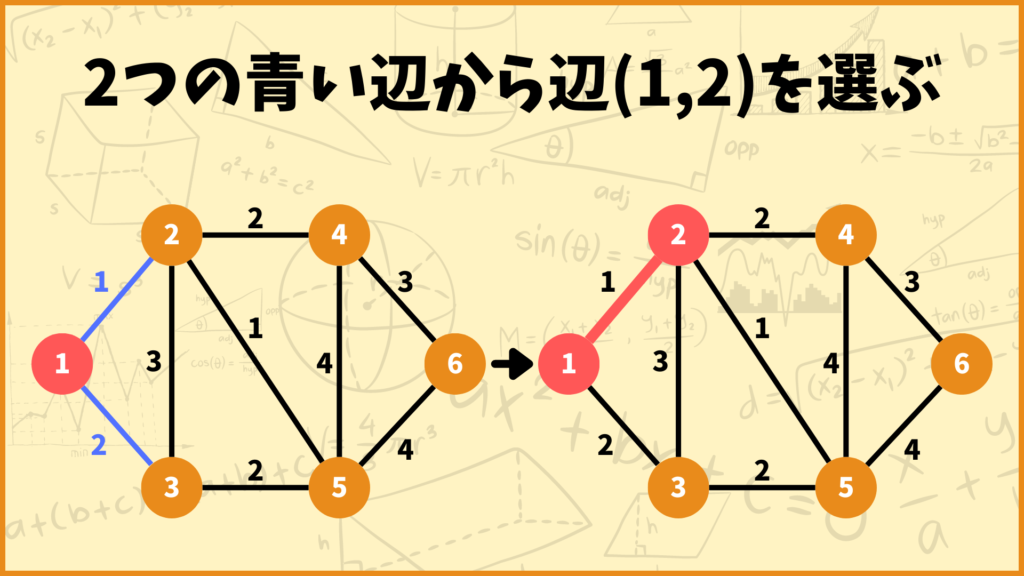
次に頂点1、頂点2とそれ以外の頂点の間にある辺の中で重みが最小のものを選びます。下のグラフで言うと、選択肢として辺\((1,3)\)、辺\((2,3)\)、辺\((2,4)\)、辺\((2,5)\)の4つがあります。
その中で辺の重みが最小なのは辺\((2,5)\)なので、辺\((2,5)\)を選び頂点5を赤色にします。
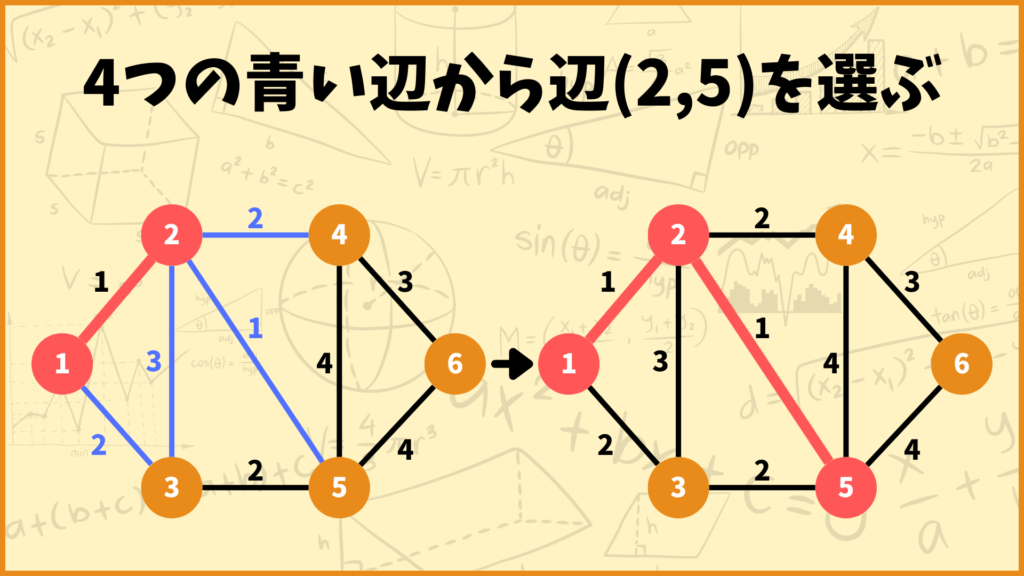
次に頂点1,2,5とそれ以外の頂点の間にある辺の中で重みが最小のものを選びます。下のグラフで言うと、選択肢として辺\((1,3)\)、辺\((2,3)\)、辺\((2,4)\)、辺\((5,3)\)、辺\((5,4)\)、辺\((5,6)\)の6つがあります。
その中で重みが最小なのは辺\((1,3)\)、辺\((2,4)\)、辺\((5,3)\)の3つです。実はプリム法では重みが最小であればどれを選んでもOKです。
今回は辺\((1,3)\)を選び、頂点3を赤色にします。
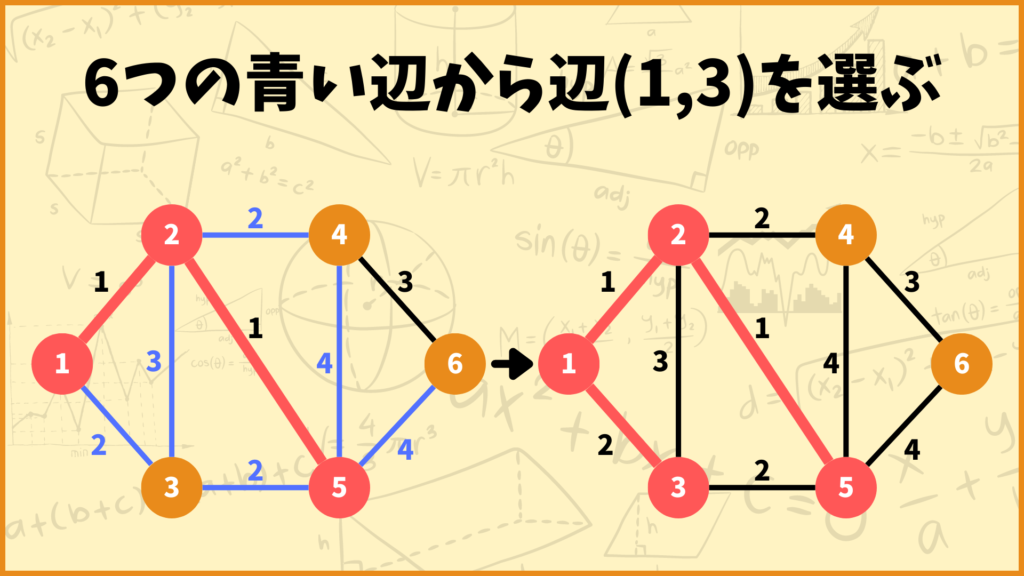
このような操作を全ての頂点が赤色になるまで実行します。ここからは言葉を省略して図だけで説明していきます。
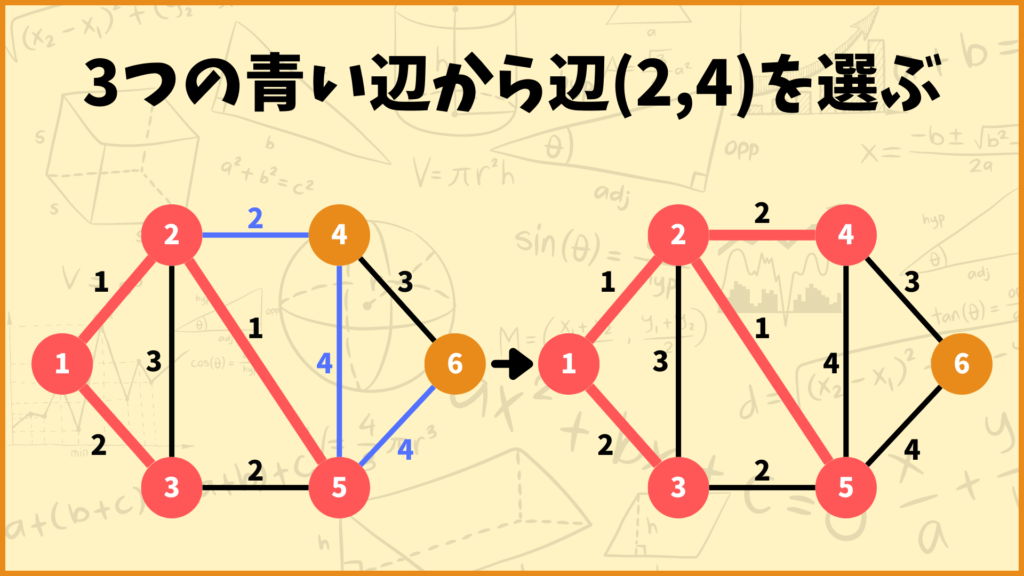
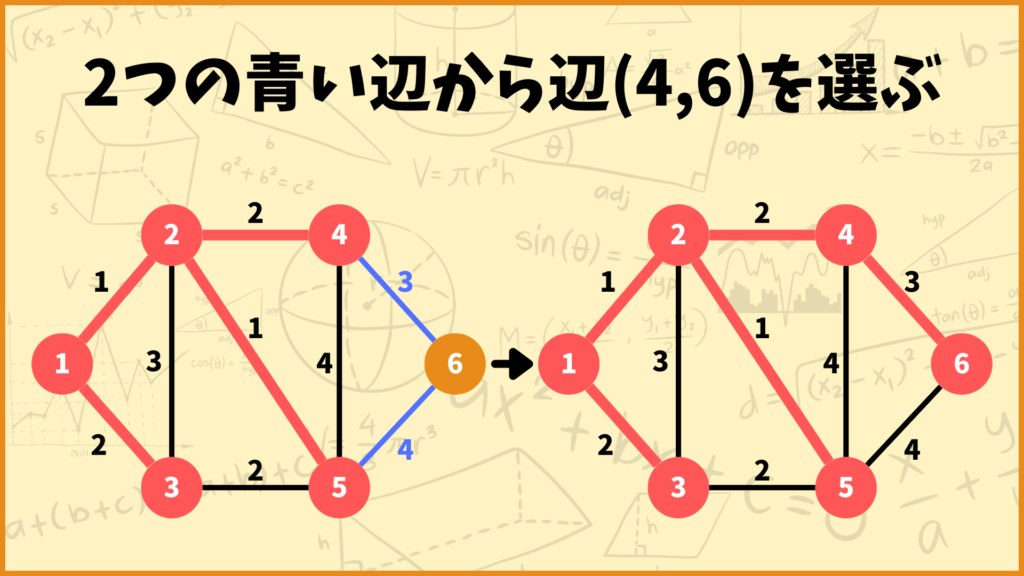
このようにして出来上がった最小全域木が一番最初の図になると言うことです。
辺の選び方を変えることで異なる最小全域木ができます。例えば先ほどの説明では辺\((1,3)\)を選びましたが、代わりに辺\((3,5)\)を選ぶとまた違った最小全域木が出来上がります。
なんでプリム法で最小全域木が求まるの?
ここからはなぜプリム法で最小全域木が求まるかについて説明していきたいと思います。この説明をするためにはいくつか事前知識が必要になるのでまずはそれらの説明からしたいと思います。
カットってなに?
まずはカットについて説明したいと思います。ある全域木\(T\)を考えたときに、全域木\(T\)中の辺を除去すると2つのグラフに分割することができます。
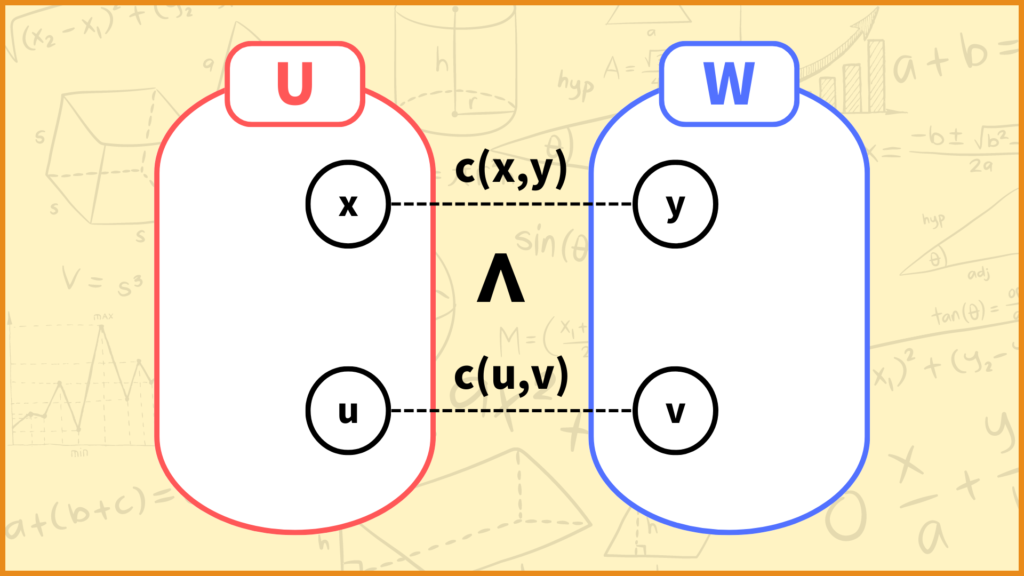
このとき2つのグラフの頂点集合をそれぞれ\(U,\;W\)としたときに\((U,W)\)のことをカットと言います。
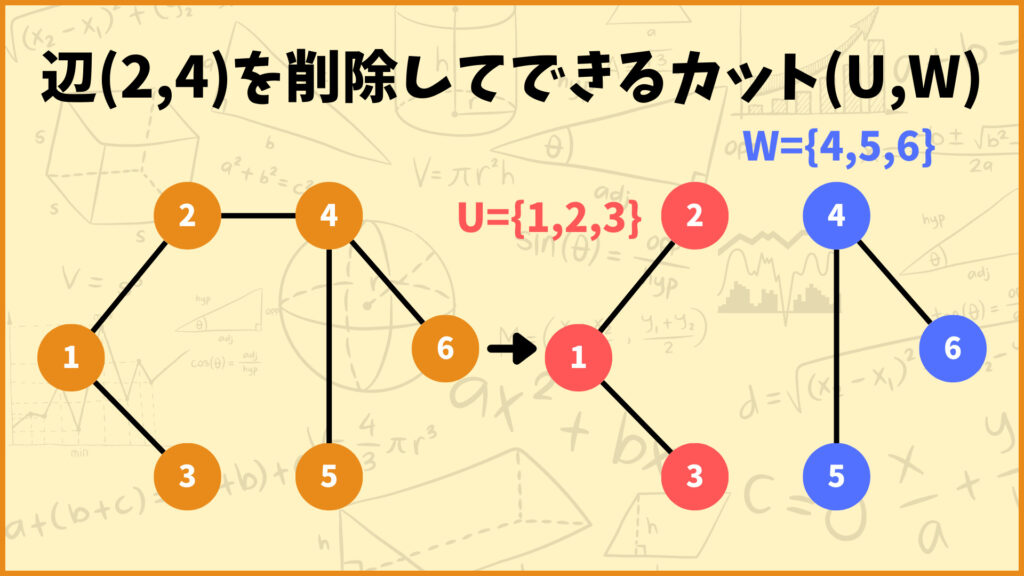
例えば上の図の全域木の辺\((2,4)\)を除去して得られるカット\((U,W)\)は\(U=\{1,2,3\}\), \(W=\{4,5,6\}\)となります。
最小全域木とカット
それでは次に最小全域木とカットについて見ていきましょう。下の最小全域木とそのカットについて考えてみます。
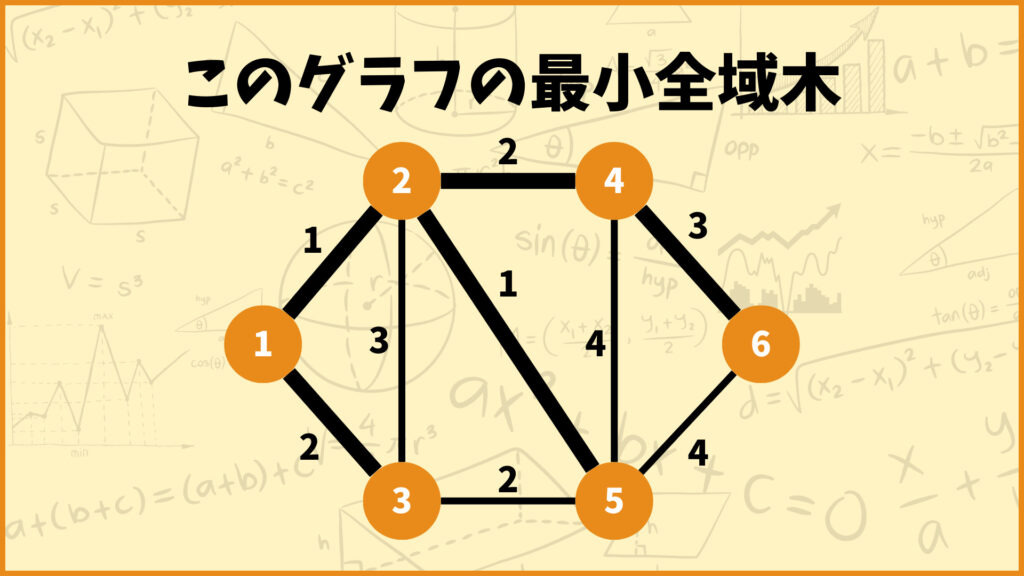
例えば辺\((1,2)\)を除去して得られるカットを考えてみましょう。
このときカット中には辺\((1,2)\)、辺\((2,3)\)、辺\((3,5)\)の3つが含まれていますね。その中で重みが最も小さい辺は辺\((1,2)\)で最小全域木に含まれている辺ですね。
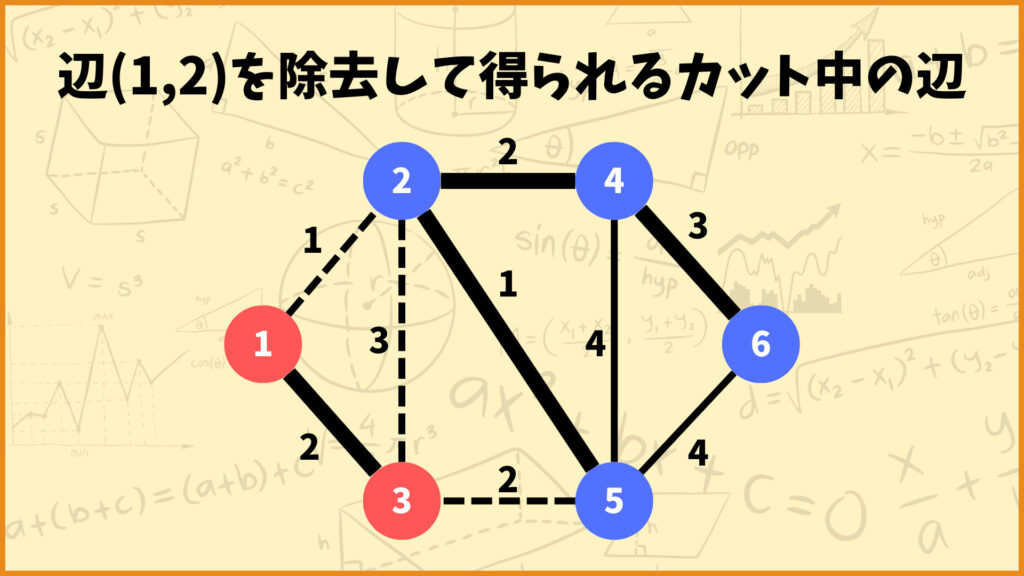
他にも例えば辺\((2,5)\)を除去して得られるカットについて考えてみましょう。
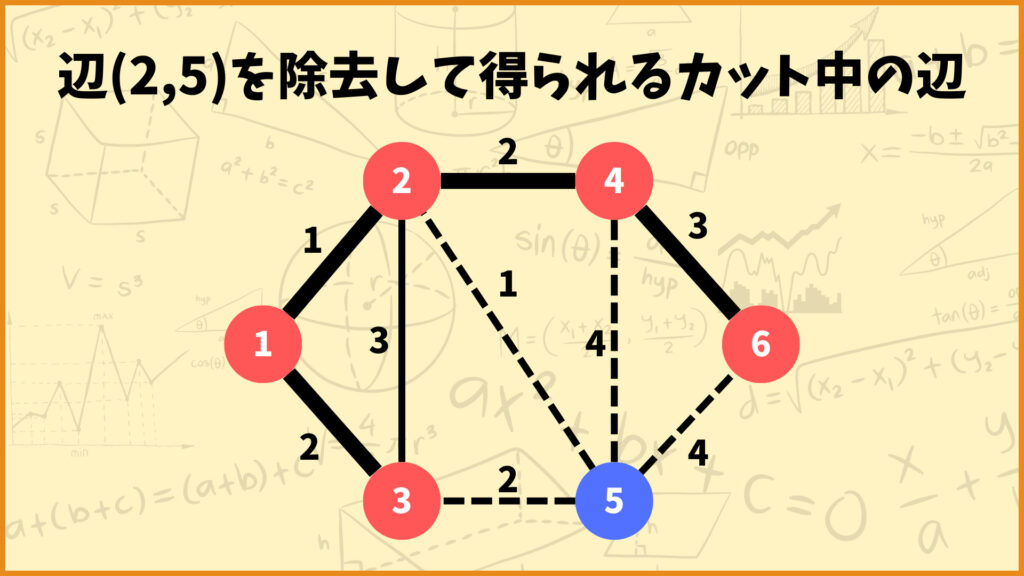
このときカット中には辺\((2,5)\)、辺\((3,5)\)、辺\((4,5)\)、辺\((5,6)\)の4つが含まれていますね。その中で重みが最も小さい辺は辺\((2,5)\)で、これもやはり最小全域木に含まれている辺ですね。
どうやらどのカットについて考えてみても、最小全域木に含まれている辺がカット中で重み最小の辺になっているようです。
このことを定理として表したのが以下の記述です。
全域木\(T\)が最小全域木であることの必要十分条件は\(T\)が以下の条件を満たすことある。
\(T\)中の任意の辺\((u,v)\)について、辺\((u,v)\)を除去して得られるカットに含まれる任意の辺\((x,y)\)に対して\(c(u,v) \leq c(x,y)\)が成立する。
但し\(c(u,v)\)は辺\((u,v)\)の重み
証明はこの下に書いてあるので興味があれば見てみてください。
「全域木\(T\)が最小全域木⇒あの条件を満たす」の証明
背理法で証明する。
\(T\)から辺\((u,v)\)を除去して得られるカット中の辺\((x,y)\)の中に\(c(u,v)>c(x,y)\)を満たすものが存在すると仮定する。
このときTから辺\((u,v)\)を除去して辺\((x,y)\)を加えたものを\(T’\)とすると、\(T’\)は\(T\)より重みの合計が小さい全域木になるので\(T\)が最小全域木であることに矛盾する。□
「あの条件を満たす⇒全域木\(T\)が最小全域木」の証明
背理法で証明する。
\(T’\)を\(T\)との共通辺が最も多い最小全域木と仮定する。(\(T \ne T’\))
\(T\backslash T’\)中の辺\((u,v)\)を考える。\(p\)を\(T’\)中の\(u-v\)路とすると\(p\)は\(T\)から辺\((u,v)\)を除去することによって生じるカット中の辺\((x,y)\)を少なくとも1つ含む。
このときあの条件より\(c(u,v)\leq c(x,y)\)となるので、\(T’\)から辺\((x,y)\)を除去して辺\((u,v)\)を加えたものを\(T”\)とすると\(T”\)も最小全域木になり仮定に矛盾する。□
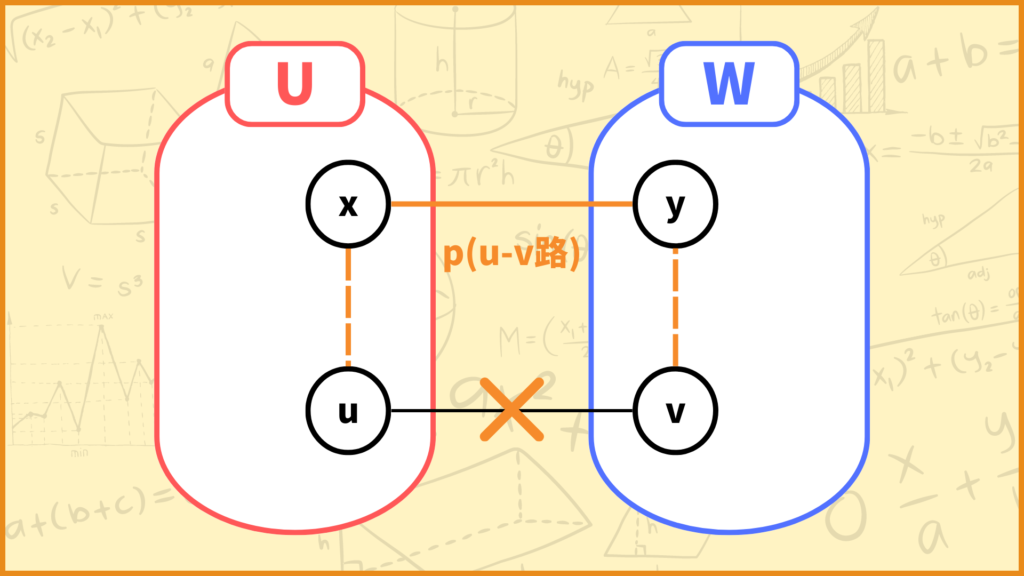
条件を満たすように辺を選ぶ
ここまでの議論から、あの条件を満たすように辺を選んでいくことで最小全域木を作ることができると言うわけです。つまりカット中の重みが最小の辺を選んでいけば最小全域木になるはずです。
これってまさにプリム法で辺を選ぶときに考えていたことですよね。
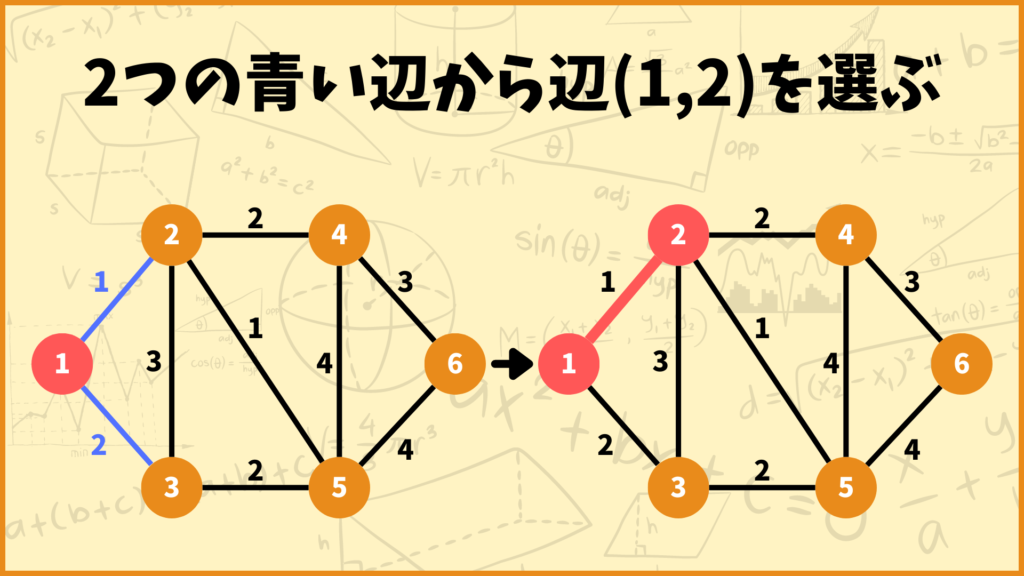
第二章でプリム法を説明したときに使った図をもう一回見てみましょう。この赤い頂点の集合とオレンジの頂点の集合をカットだと考えます。
例えばこの図で言うとカット\((U,W)\)は\(U=\{1\},\;W=\{2,3,4,5,6\}\)となります。この\((U,W)\)中には辺\((1,2)\)と辺\((1,3)\)がありますが、さっきの条件を満たすような辺、つまり重みが最小になる辺を選びたいので辺\((1,2)\)を選びます。
実はプリム法はこのように、さっきの条件を満たすように辺をどんどん選んでいるんです。そのため最終的には最小全域木を作ることができるんですね。
おわりに
いかがでしたか。
今回の記事ではプリム法について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。