こんにちは!しゅんです!
いきなりですが皆さんはいま運送会社の従業員で、これからトラックにどんな荷物を積めば良いかを考えてもらいます。

積みたい荷物はたくさんあるけどトラックの容量は決まっているので全部を積むことはできません。こんなときはどの荷物を積むのがいちばん良いのでしょうか。今回の記事ではこんな問題を数学を使って解いてみたいと思います!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
問題設定
それではまず今回考える問題をちゃんと設定しましょう。
問題設定
・倉庫に20個の荷物があり、それらの中からいくつかをトラックで運ぶことを考える。
・トラックに積める荷物は合計で300kgまで。
・荷物は「書籍」、「食料品」、「家電」、「家具」の4つのグループのいずれかに属す。
・それぞれの荷物は既知であり、以下の通りである。

目的
・なるべく多くの荷物を詰め込みたい。
今回は上記の問題を整数計画問題として定式化してpythonで解いてみたいと思います!
整数計画問題として定式化
「記号の設定」、「目的関数の設定」、「制約条件の設定」の3つに分けて説明したいと思います。
記号の設定
パラメータとして荷物の集合と荷物の重さを設定します。変数は0-1変数\(x_i\)を使いたいと思います。
パラメータ:
\(I\) : 荷物の集合
\(w_i\) : 荷物\(i\)の重さ
変数:
\(x_i \in \{0,1\}\) : 荷物\(i\)をトラックに積むなら1、そうでないなら0をとる変数
目的関数の設定
目的関数:\(\sum\limits_{i \in I}x_i \)

例えば荷物4,8,10をトラックに積む場合を考えましょう。このとき\(x_4 = x_8 = x_{10} = 1\)となります。そして目的関数値は
\(\sum\limits_{i \in I}x_i = x_4 + x_8 + x_{10} = 3\)
となります。この値はトラックに積んだ荷物の個数と対応していますね。今回はなるべく荷物を積みたいので、目的関数を最大化することを考えます。
\( \max \;\;\; \sum\limits_{i \in I}x_{i}\)
制約条件の設定
制約条件:\(\sum\limits_{i \in I}w_ix_i \leq 300 \)
制約条件は
「トラックに積める荷物の重さの合計は300kg以下」
です。これを数式で表すと上記のようになります。

例えば荷物3,8,10をトラックに積む場合を考えましょう。このとき\(x_4 = x_8 = x_{10} = 1\)となります。そして制約条件の左辺は
\(\sum\limits_{i \in I}w_i x_i = w_4 x_4 + w_8 x_8 + w_{10}x_{10} = 44\)
となり、荷物4,8,10の重さの合計を表しています。これが300以下になれば良いので上記のような制約条件になります。
整数計画問題としてまとめる
以上のことを踏まえて整数計画問題として定式化しましょう。
パラメータ:
\(I\) : 荷物の集合
\(w_i\) : 荷物\(i\)の重さ
変数:
\(x_i \in \{0,1\}\) : 荷物\(i\)をトラックに積むなら1、そうでないなら0をとる変数
\(\max \;\;\; \sum\limits_{i \in I}x_i\)
\(\;\text{s.t.}\;\;\;\sum\limits_{i \in I} w_ix_i \leq 300\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;( \forall i \in I)\)
pythonで解いてみる
それでは実際にこの問題をpythonで解いてみましょう。結論以下のコードを実行することで問題を解くことができます。
## 事前準備
!pip install pulp # pulpをインストール
from pulp import *
## 記号の定義
I = [i for i in range(20)] # 荷物の集合
w = [5, 19, 25, 3, 9, 4, 16, 25, 15, 16, 46, 38, 32, 29, 41, 26, 38, 39, 45, 50] # 重さの集合
## 整数計画問題として定式化
prob = pulp.LpProblem(sense = LpMaximize) # 問題をMaximizeに設定
x = LpVariable.dict("x",I, cat = "Binary") # 0-1変数の設定
prob += lpSum(x[i] for i in I) # 目的関数の設定
prob += lpSum(w[i] * x[i] for i in I) <= 300 # 制約条件を設定
result = prob.solve() # 問題を解く
## 結果の表示
print(LpStatus[result]) # 得られた結果の状態を表示(Optimalなら最適解が得られている)
for i in I:
if x[i].value() == 1:
print(f"x{i} =",x[i].value()) # 最適解(変数の値が1のものだけ)を表示
print("最適値 :", prob.objective.value()) # 最適値を表示
このコードを実行したら以下の結果が得られました。

コードの説明と結果の解釈の2つに分けて話したいと思います。
コードの説明
事前準備
## 事前準備
!pip install pulp # pulpをインストール
from pulp import *
問題を解くための事前準備としてpulpをインストール、インポートします。pulpはpythonで数理計画問題を解くのに便利なやつです。2行目でpulpのインストール、3行目でpulpのインポートを行っています。
記号の定義
## 記号の定義
I = [i for i in range(20)] # 荷物の集合
w = [5, 19, 25, 3, 9, 4, 16, 25, 15, 16, 46, 38, 32, 29, 41, 26, 38, 39, 45, 50] # 重さの集合
5~7行目では記号の定義をしています。6行目で荷物の集合\(I\)、7行目で荷物\(i\)の重さ\(w_i\)をそれぞれリスト形式で設定しています。
整数計画問題として定式化
## 整数計画問題として定式化
prob = pulp.LpProblem(sense = LpMaximize) # 問題をMaximizeに設定
x = LpVariable.dict("x",I, cat = "Binary") # 0-1変数の設定
prob += lpSum(x[i] for i in I) # 目的関数の設定
prob += lpSum(w[i] * x[i] for i in I) <= 300 # 制約条件を設定
result = prob.solve() # 問題を解く
9~15行目で整数計画問題として定式化しています。
10行目では問題を最大化(Maximize)に設定しています。
11行目では変数の設定をしています。かっこの中身は左から順に(“変数名”, 添字の集合, 変数の種類)となっています。変数名はx、添字の集合はさっき定義したI、cat = “Binary”で変数を0-1変数としています。
12行目では目的関数を設定しています。\(\sum\)はlpSumで表現できます。
13行目では制約条件を設定しています。
15行目で問題を解いています。
結果の表示
## 結果の表示
print(LpStatus[result]) # 得られた結果の状態を表示(Optimalなら最適解が得られている)
for i in I:
if x[i].value() == 1:
print(f"x{i} =",x[i].value()) # 最適解(変数の値が1のものだけ)を表示
print("最適値 :", prob.objective.value()) # 最適値を表示
17~22行目で計算結果を表示しています。
18行目で解の状態を表示しています。Optimalと表示されたら最適解が得られています。
19~21行目で最適解を表示しています。for文で全ての荷物のインデックスを取得して、変数の値が1のものだけ表示するようにしています。
22行目で最適値を表示しています。
結果の解釈

1行目は無視して大丈夫です。(pulpがちゃんとインストールされていることを示しています。)
2行目でOptimalと返されているのでちゃんと最適解が得られていることが分かります。
3~17行目は最適解を表しています。pythonはデフォルトだと0から数字が始まるので、x0=1.0は荷物1をトラックに積むことを表しています。

18行目は最適値が表示されています。最適値が15なので最大で15個の荷物をトラックに積めることが分かりました。
荷物のグループに偏りがある
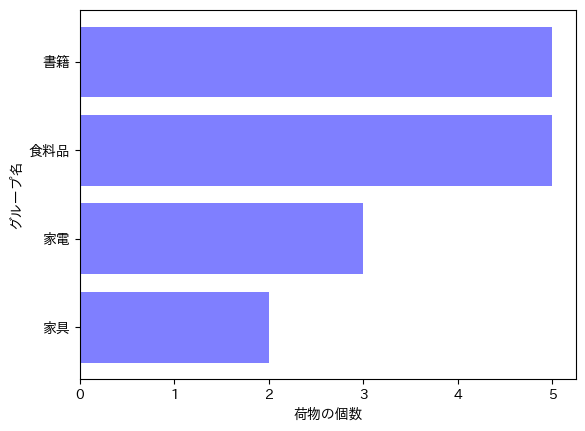
最適解が得られたんですけど、これだと書籍と食料品は5つ全てトラックに積める一方で、家具は2つしか積めていないですね。この問題を解決するために、「最も荷物を積むことができていないグループに属す、トラックに積む荷物の個数を最大にする」という定式化をする必要がありそうです。
結論以下のように混合整数計画問題として定式化することで目的が達成されます。
パラメータ:
\(G\) : グループの集合
\(I\) : 荷物の集合
\(I_g\) : グループ\(g\)に属す荷物の集合
\(w_i\) : 荷物\(i\)の重さ
変数:
\(x_i \in \{0,1\}\)
\(t\)
\(\max \;\;\; t\)
\(\;\text{s.t.}\;\;\;\sum\limits_{i \in I_g} x_i \geq t \;\;( \forall g \in G)\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in I} w_ix_i \leq 300\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;( \forall i \in I)\)
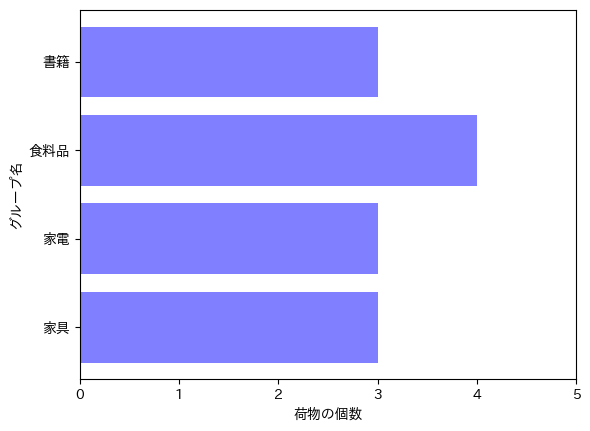
上記の問題を解いた結果が上図です。これを見るとどのグループの荷物も満遍なく積めていることが分かりますね。
詳しい説明はこちらの記事で解説しています!
おわりに
いかがでしたか。
今回の記事では数学が世の中で使える例について解説していきました。
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。




