- 時系列データってなに?
- 相互相関ってなに?
- 相互相関をpythonで実装したい…
こんにちは!しゅんです!
今回は相互相関について解説していきます!またpythonでの実装方法についても解説します!
それではやっていきましょう!
【Udemy講座公開のお知らせ】
このたびUdemyで数理最適化の講座を公開しました!この講座は「数理最適化を勉強してみたいけど数式が多くて難しい…」という方向けに、どうやって最適化問題を定式化すれば良いかを優しく丁寧に解説しています!
時系列データってなに?
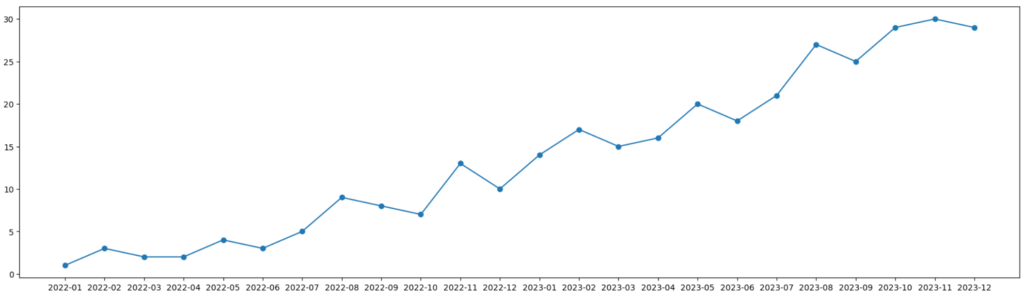
時系列データを簡単に説明すると時間軸に沿って順番に並んだデータのことです。例えば上図のデータは時系列データです。横軸が月で、その月ごとにデータがプロットされていますね。
時系列データの例としては
- 毎日の気温
- 毎月の売上高
- 毎週の交通量
などが挙げられます。今回は2つの異なる時系列データ間の関係を調べる手法の1つである、相互相関について解説していきます。
相互相関ってなに?
相互相関を一言で説明すると
時間差を考慮した2つの時系列データ間の類似度
です。相互相関は-1から1のいずれか値を取ります。相互相関の大きさと時系列データ間の類似度の関係は以下の通りです。
- 相互相関が1に近い:データがほぼ同じ動きをする
- 相互相関が0に近い:2つのデータの動きがほぼ無関係
- 相互相関が-1に近い:データがほぼ逆動きをする
相互相関は複数の時系列データの関係を調査したり、時系列データの予測などで使用されます。言葉で説明されてもよく分からないので、具体例を使って相互相関を見ていきましょう。
もう少し正確に言うと、正規化した相互相関は-1以上1以下の値を取ります。
具体例を使って相互相関を説明する
具体例その1
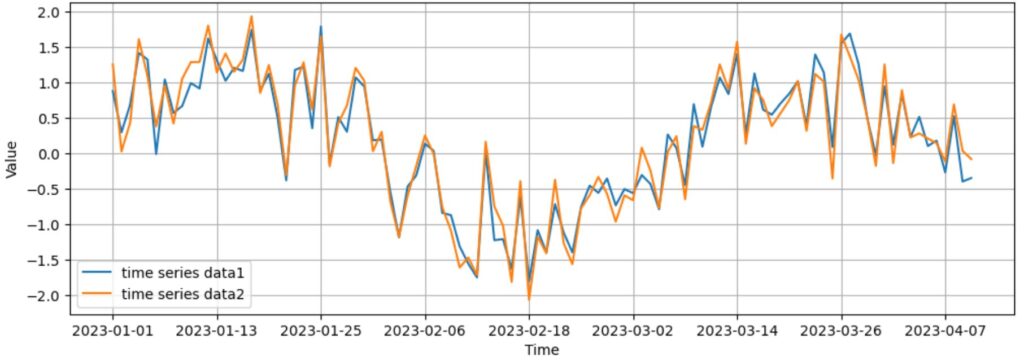
例えば上のグラフを見てみましょう。上のグラフは2種類の時系列データをグラフにしたものです。横軸が日付、縦軸がデータ値を表しています。これを見るとこの2つの時系列データが同じような動きをしていることが分かりますね。
相互相関を計算することで上図のような時系列データがどれくらい類似しているかを知ることができます。上の2つのデータだと、おそらく相互相関の値は1に近いと思われます。
具体例その2
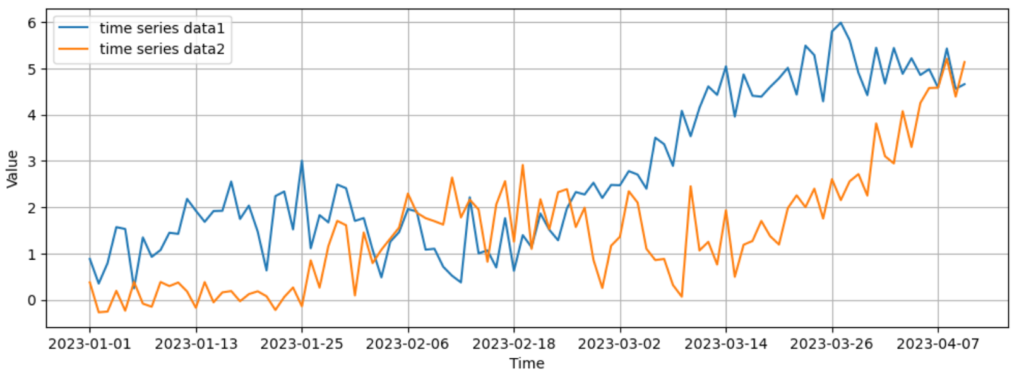
今度は上図のグラフを見てみましょう。こちらも2種類の時系列データをグラフにしたものです。一見するとこの2つの時系列データは同じ動きをしていないように見えますね。ここでオレンジのデータを左側に25日ずらしてみましょう。
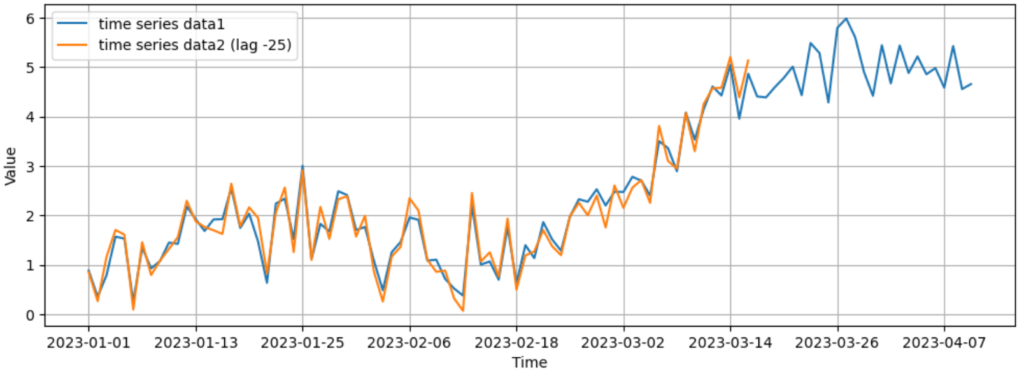
上図はオレンジのデータだけ左側に25日だけずらしたグラフです。これを見るとこの2つの時系列データが同じような動きをしていることが分かります。
上のデータの場合、時間差を25日にしたときの相互相関の値は1に近いと思われます。一方で時間差が0日のときの相互相関の値は大きくも小さくもないと思われます。
時間差のことをラグ(lag)と言ったりします。
自己相関と相互相関の違い
相互相関と似た用語で自己相関というものがあります。これらの違いは下記の通りです。
- 自己相関:過去の自分と今の自分がどれくらい似ているか?
- 相互相関:他のデータと自分がどれくらい似ているか?
自己相関は1種類の時系列データに対して計算するものですが、相互相関は2種類の異なる時系列データに対して計算するものです。ただどちらも時間差を考慮した時系列データの類似度を計算することは共通しています。
\\\ 自己相関はこちらの記事で詳しく解説しています! ///
具体例を使って相互相関を計算してみる
それでは具体例を使って相互相関を計算していきましょう。
相互相関の計算に使う2つの時系列データを用意する

今回は上記の2つの時系列データを使って相互相関を計算したいと思います。これらのデータは2つとも2023年1月1日~2023年1月20日までの20個のデータです。グラフにすると下図のようになります。
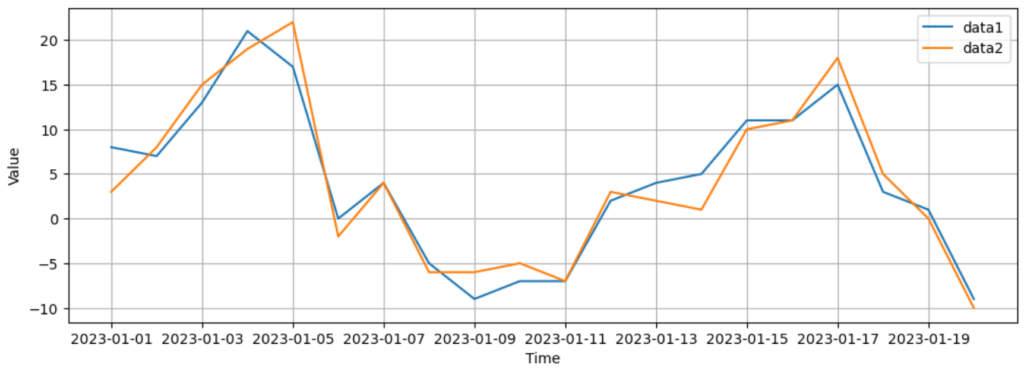
この2つのデータは同じような動きをしていますね。おそらく相互相関の値は1に近い値を取ると考えられます。
ラグを設定する
それでは次にラグを設定します。今回は簡単のためラグを0とします。これはラグ0で2つのデータが連動しているように見えるためです。
実際の分析ではラグを一定範囲で動かしたときの(例えば-10から10まで動かす)相互相関の値の変化をグラフ(コレログラム)にしたりします。この記事でも第5章のpythonでの実装の所で詳しく説明しています。
相互相関を計算する
それでは実際に相互相関を計算していきましょう。相互相関の計算式は下記の通りです。
2つの時系列データ \((x_1,x_2,…,x_n)\) と \((y_1,y_2,…,y_n)\) があるときに、ラグ0の相互相関は以下の式で計算できる。
\(\frac{\sum\limits_{i=1}^{n}x_iy_i}{\sqrt{\sum\limits_{i=1}^{n}x_i^2 \times \sum\limits_{i=1}^{n}y_i^2}}\)
なおこの計算式はpythonのmatplotlibのxcorr関数での計算方法を参考にしています。

ではまず分子の \(\sum\limits_{i=1}^nx_iy_i\) から計算していきましょう。上のデータを使うので \(n=20\) となります。また、例えば \(x_1=8,y_1=3\) となります。従って分子は
\(\sum\limits_{i=1}^nx_iy_i=(8\times3)+(7\times8)+…+((-9)\times(-10))=1857\)
と計算できます。次に分母の2つの式を計算しましょう。
\(\sum\limits_{i=1}^nx_i^2=8^2+7^2+…+(-9)^2=1835\)
\(\sum\limits_{i=1}^ny_i^2=3^2+8^2+…+(-10)^2=1993\)
従ってラグ0の相互相関は
\(\frac{\sum\limits_{i=1}^{n}x_iy_i}{\sqrt{\sum\limits_{i=1}^{n}x_i^2 \times \sum\limits_{i=1}^{n}y_i^2}} = \frac{1857}{\sqrt{1835\times1993}}=0.9710…\)
と計算することができます。これを見るとほぼ1に近い値を取っているので、この2つの時系列データはほぼ同じ動きをするということが分かりました。
ラグが \(k\)のとき(オレンジのデータを右に \(k\) だけずらすとき)の相互相関の計算式は
\(\frac{\sum\limits_{i=1}^{n-k}x_{i+k}y_i}{\sqrt{\sum\limits_{i=1}^{n}x_i^2 \times \sum\limits_{i=1}^{n}y_i^2}}\)
で計算できます。分子だけちょっと変わっていますね。
pythonで相互相関を計算してみる
## 事前準備
import numpy as np
import matplotlib.pyplot as plt
## 時系列データの準備
x = np.array([8, 7, 13, 21, 17, 0, 4, -5, -9, -7, -7, 2, 4, 5, 11, 11, 15, 3, 1, -9])
y = np.array([3, 8,15, 19, 22, -2, 4, -6, -6, -5, -7, 3, 2, 1, 10, 11, 18, 5, 0, -10])
## 相互相関を計算してグラフを表示する
xcorr = plt.xcorr(x, y, maxlags=10)
plt.xticks(np.arange(-10,11,2))
plt.xlabel("lag")
plt.ylabel("correlation coefficient")
plt.show()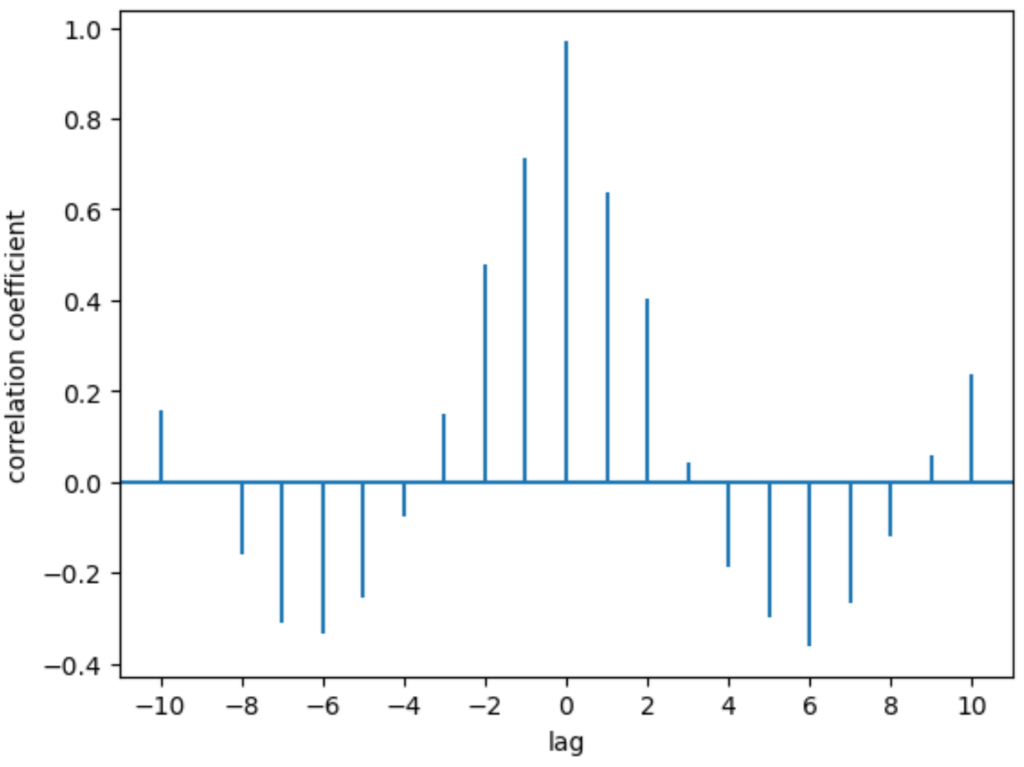
それでは実際にpythonで相互相関を計算していきましょう。上記のコードがpythonで相互相関を計算するコードです。このコードを実行したら上のグラフが得られました。コードと結果を1つずつ解説していきます。
事前準備
## 事前準備
import numpy as np
import matplotlib.pyplot as plt
事前準備として「numpy」と「matplotlib」をインポートします。
「numpy」はこの後時系列データを作成するときとグラフのx軸を設定するときに使います。
「matplotlib」は相互相関を計算し、結果をグラフで表示するために使います。
時系列データの準備
## 時系列データの準備
x = np.array([8, 7, 13, 21, 17, 0, 4, -5, -9, -7, -7, 2, 4, 5, 11, 11, 15, 3, 1, -9])
y = np.array([3, 8, 15, 19, 22, -2, 4, -6, -6, -5, -7, 3, 2, 1, 10, 11, 18, 5, 0, -10])
ここでは2つの時系列データを用意しています。第4章と同じデータを作成しました。データは「numpy」の「.array()」で作成しています。グラフにすると下図のようになります。
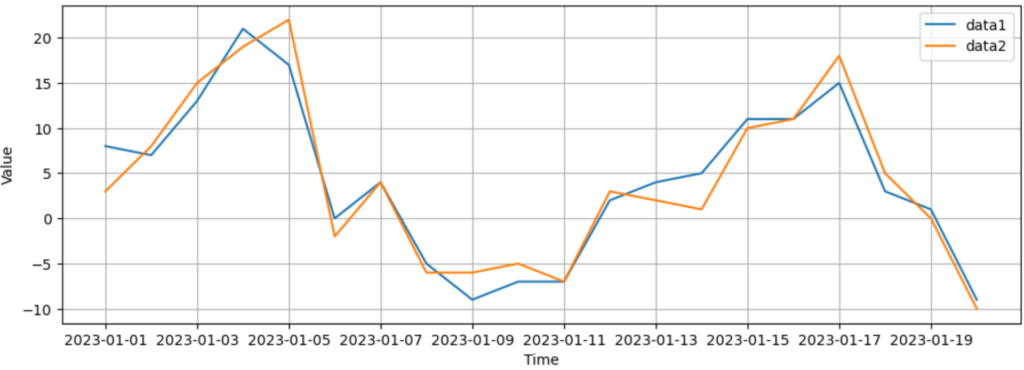
import datetime
import numpy as np
import matplotlib.pyplot as plt
## 時系列データの準備
x = np.array([8, 7, 13, 21, 17, 0, 4, -5, -9, -7, -7, 2, 4, 5, 11, 11, 15, 3, 1, -9])
y = np.array([3, 8, 15, 19, 22, -2, 4, -6, -6, -5, -7, 3, 2, 1, 10, 11, 18, 5, 0, -10])
## 日付データの作成
start_date = datetime.date(2023, 1, 1)
date_list = [start_date + datetime.timedelta(days=i) for i in range(len(x))]
## グラフを作成する
plt.figure(figsize=(12, 4))
plt.plot(date_list, x, label='data1')
plt.plot(date_list, y, label='data2')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.grid(True)
plt.show()相互相関を計算してグラフを表示する
## 相互相関を計算してグラフを表示する
xcorr = plt.xcorr(x, y, maxlags=10)
plt.xticks(np.arange(-10,11,2))
plt.xlabel("lag")
plt.ylabel("correlation coefficient")
plt.show()
この部分では相互相関を計算してグラフを表示しています。
2行目で相互相関を計算しています。相互相関は「matplotlib」の「.xcorr()」で計算できます。引数は相互相関を計算したい時系列データ「x」と「y」、そして「maxlag」です。
「maxlag」はラグの最大値を設定します。いま「maxlag=10」としているので、-10~10までのラグ(合計21個)で相互相関を計算します。
3行目ではx軸の目盛りを設定をしています。「np.arange(-10,11,2)」と設定することで目盛りを-10から10まで2刻みで表示するように設定しています。
4行目でx軸のラベルを「lag」としています。
5行目でy軸のラベルを「correlation coefficient」としています。
6行目でグラフを表示しています。
結果を確認する

結果を確認してみましょう。このグラフの横軸はラグ、縦軸は相互相関の値を表しています。これを見るとラグ0の時の値が1に近い値となっていますね。実際に数値を確認してみましょう。

for i in range(len(xcorr[1])):
print(f"ラグ{xcorr[0][i]}のときの相互相関の値:{xcorr[1][i]}")
これを見るとラグが0のときの相互相関の値は0.97104693…となっていて、第4章で計算した値と同じになっています。このことから今回用意した2つの時系列データはラグ0でほぼ同じ動きをしていることが分かりました。
他のデータを使って相互相関を計算する
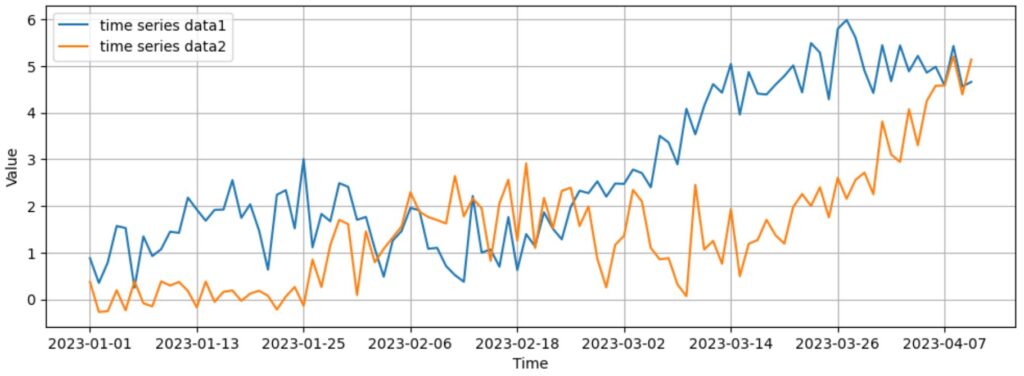
最後に他のデータを使って相互相関を計算してみましょう。今度は下の2つの時系列データを使います。
import numpy as np
import matplotlib.pyplot as plt
import datetime
# 時系列データの長さ
data_length = 100
# 乱数系列の生成 (共通のノイズ)
np.random.seed(0)
noise = np.random.randn(data_length)
# 長期的な上昇トレンド
trend = np.linspace(0, 5, data_length)
# 時系列データ1の作成
data1 = np.sin(np.linspace(0, 10, data_length)) + 0.5 * noise + trend
# 時系列データ2の作成 (データ1にラグを加えて若干のノイズを加える)
lag = 25
data2 = np.concatenate((np.zeros(lag), data1[:-lag])) + 0.2 * np.random.randn(data_length)
# 日付データの作成
start_date = datetime.date(2023, 1, 1)
date_list = [start_date + datetime.timedelta(days=i) for i in range(data_length)]
# 図示
plt.figure(figsize=(12, 4))
plt.plot(date_list, data1, label='time series data1')
plt.plot(date_list, data2, label='time series data2')
plt.xlabel('Time')
plt.ylabel('Value')
plt.xticks(date_list[::data_length // 8])
plt.legend()
plt.grid(True)
plt.show()
このデータは100日間の時系列データとなっています。このデータを使って相互相関を計算していきましょう。
トレンドがあるからそのまま相互相関を計算してもうまくいかない
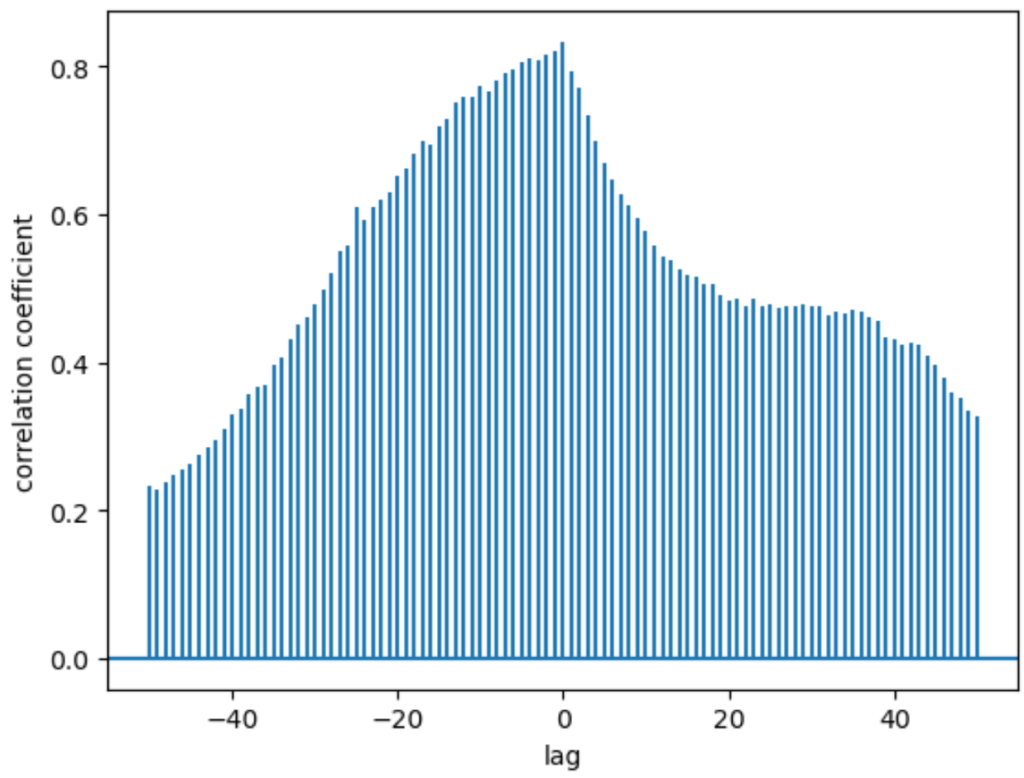
xcor_value = plt.xcorr(data1, data2, maxlags=50)
plt.xlabel("lag")
plt.ylabel("correlation coefficient")
plt.show()
ということでラグを-50から50まで動かして相互相関を計算してグラフにしてみました。これを見ると先ほどと異なる形をしていることが分かります。
結論これはうまくいってないです。なぜかと言うと
データに上昇トレンドが存在するから
です。
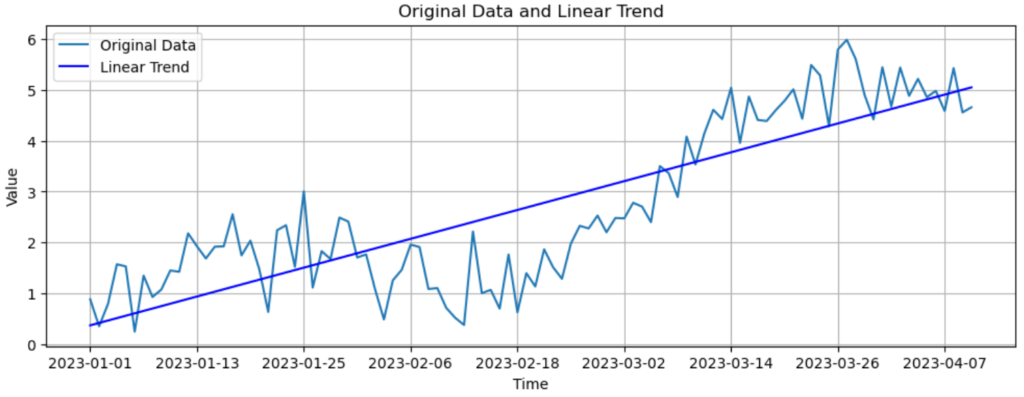
上図を見たら分かるように、今使ってる時系列データは長期的には値が上昇する傾向がありますね。これをトレンドと言いますが、このトレンドが相互相関に影響を及ぼしてしまい上手く分析ができないんです。
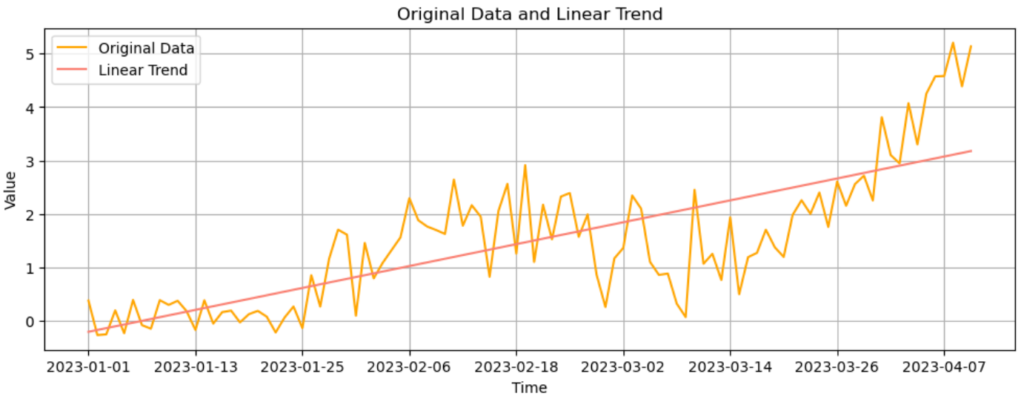
オレンジのデータも同じように上昇トレンドがありますね。
\\\ 時系列データのトレンドはこの記事で詳しく解説しています! ///
トレンドを除去して相互相関を計算する
この問題を解決するためには上昇トレンドを除去して相互相関を計算する必要があります。これは「xcorr」メソッドの引数「detrend」で設定できます。
例えば以下のように設定することで直線のトレンドを除去して相互相関を計算することができます。
from matplotlib import mlab
# 相互相関コレログラム(上昇トレンドを除去)
xcor_value = plt.xcorr(data1, data2, detrend=mlab.detrend_linear, maxlags=50)
plt.xlabel("lag")
plt.ylabel("correlation coefficient")
plt.xticks(np.arange(-50,51,25))
plt.show()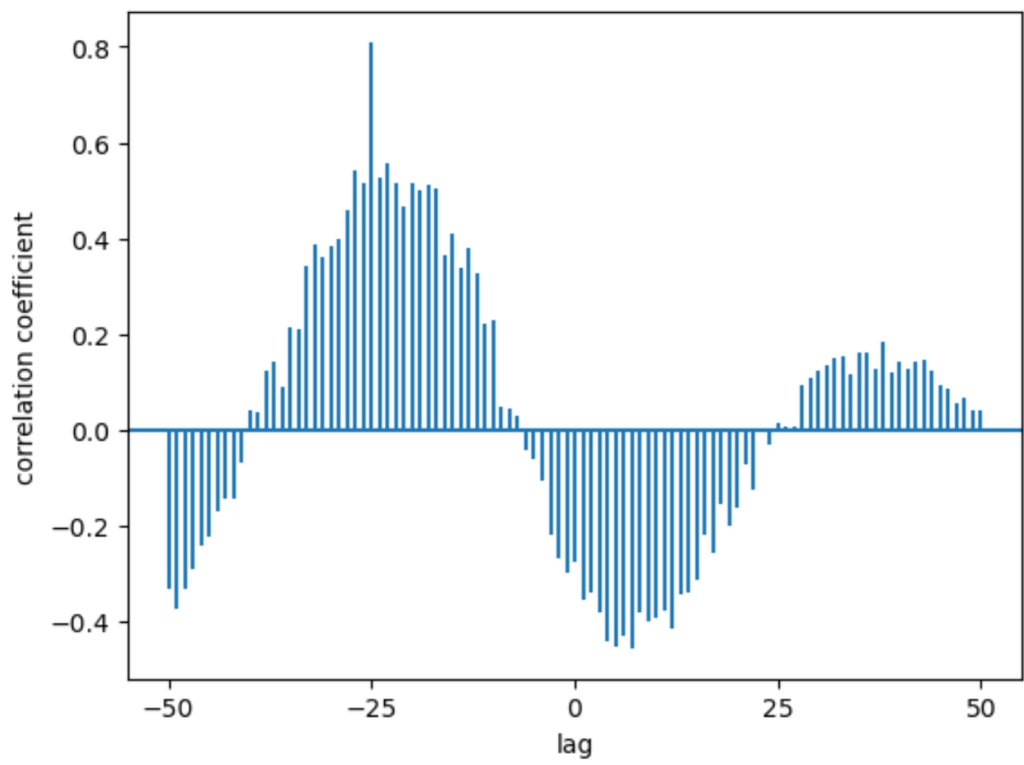
上図のグラフはトレンドを除去して相互相関を計算したときの結果を表しています。横軸がラグ(-50から50まで)縦軸が相互相関の値をそれぞれ表しています。
これを見るとlagが-25の所で相互相関が0.8辺りを取っていますね。これは2つのデータが25日ずれてほぼ同じ動きをしているということを表しています。

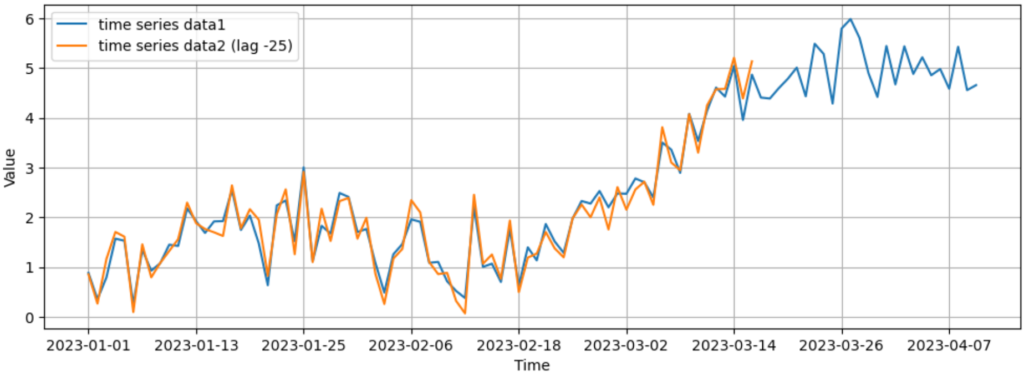
上側の図は元データを表しており、下側の図はオレンジのデータだけを25日左側にずらしたときを表しています。下側の図を見ると2つのデータが同じ動きをしていることが分かります。
このようにラグと相互相関の関係をグラフにすれば、一見連動していないように見える2つの時系列データが実は時期がずれて連動しているという事実を発見できます。
おわりに
いかがでしたか。
今回の記事では相互相関について解説しました。
今後もこのようなデータ分析に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。






