【これでわかる！】pythonで時系列データを季節性やトレンドに分解する方法をなるべくわかりやすく解説してみた

こんにちは！しゅんです！

今回は時系列データを季節性やトレンドに分解する方法について解説していきます！またpythonでの実装方法についても解説します！

それではやっていきましょう！

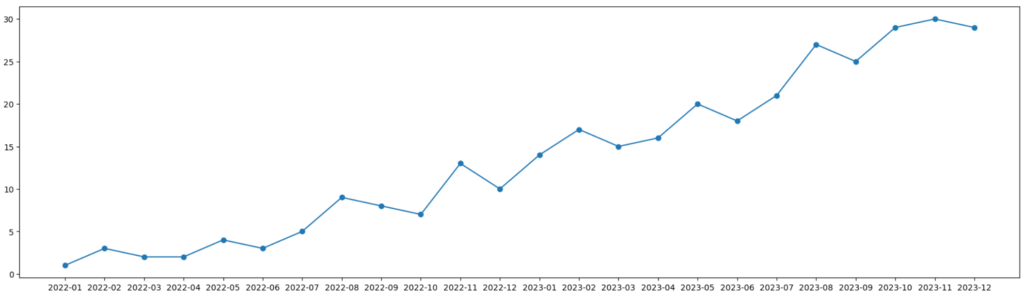
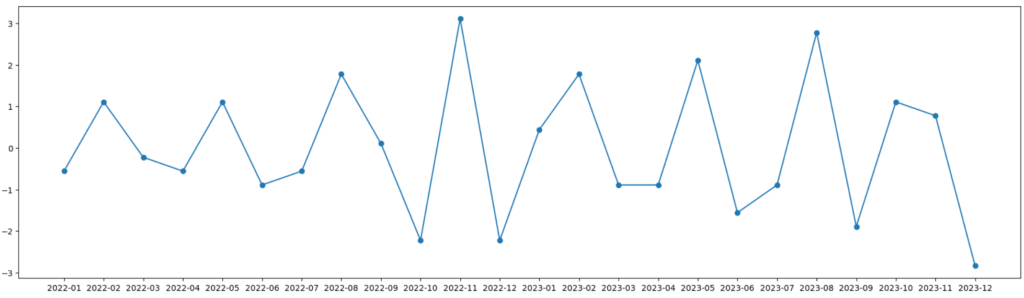
時系列データを簡単に説明すると時間軸に沿って順番に並んだデータのことです。例えば上図のデータは時系列データです。横軸が月で、その月ごとにデータがプロットされていますね。

時系列データの例としては

などが挙げられます。今回はこの時系列データを分析する手法の1つを説明していきます。

上図のような時系列データを見ると、上がったり下がったり複雑な動きをしているのが分かります。時系列データの分析手法の1つとして、この複雑な動きをトレンド、季節性、残差の3つに分解するという手法があります。

トレンドってなに？

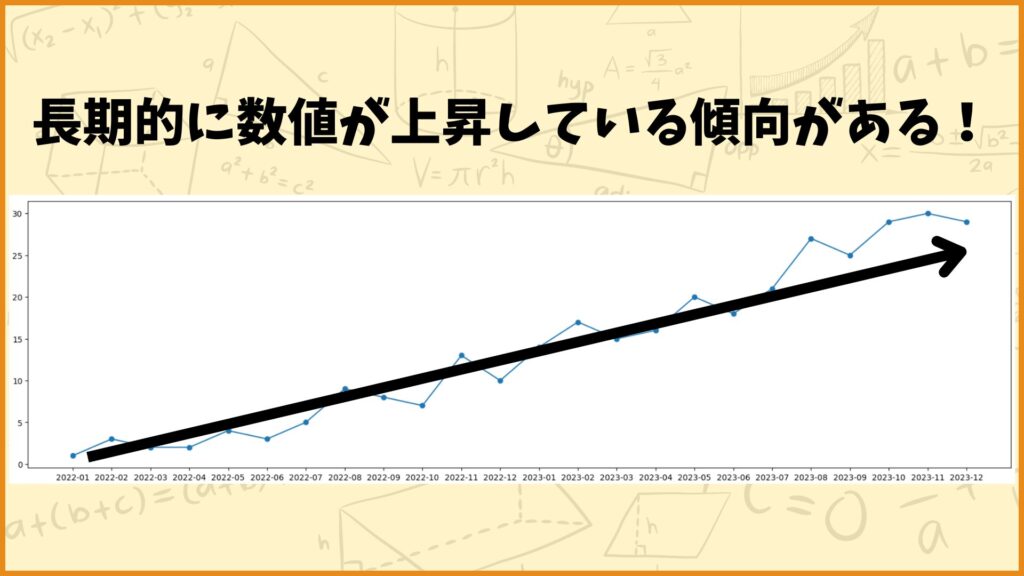
例えばさっきの時系列データを見てみましょう。このデータは短期的には上がったり下がったりしていますが、長期的に見ると数値が上昇している傾向が見られますね。このことをトレンドと言います。

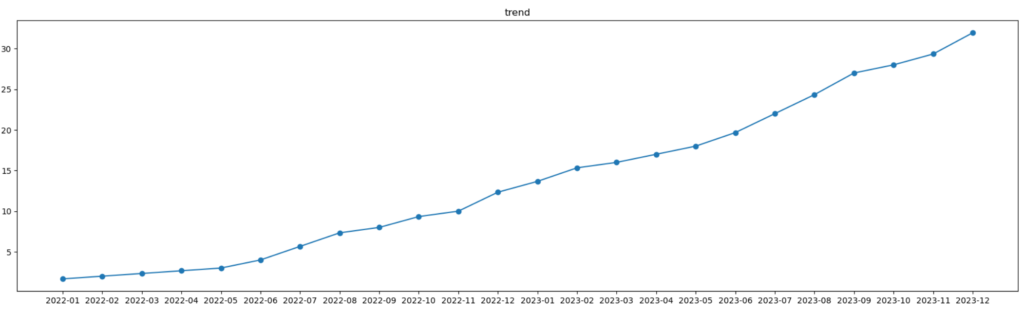
後で求め方は説明しますが、さっきの時系列データからトレンドだけを抽出すると上図のようなグラフになります。

季節性ってなに？

引き続きさっきの時系列データを見てみましょう。このデータをよく見てみると、3カ月周期で山が存在していることが分かります。

つまりこの時系列データは「低い→高い→低い」を繰り返すようなデータになっています。これを季節性と言います。

後で求め方は説明しますが、さっきの時系列データから季節性だけを抽出すると上図のようなグラフになります。季節性だけを抽出したデータは3カ月周期で同じデータを繰り返します。

残差ってなに？

残差はトレンドと季節性では説明できない不規則な変動で

\(\text{残差}=\text{元データ}-\text{トレンド}-\text{季節性}\)

で計算します。例えばある月の元データの値が\(5\)、トレンドデータの値が\(3\)、季節性データの値が\(4\)だとすると、その月の残差データの値は

\(\text{残差}=5-3-4=-2\)

と計算できます。

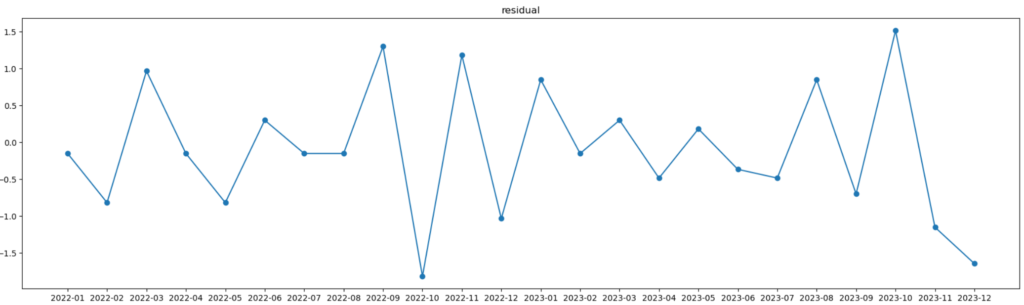
後で求め方は説明しますが、さっきの時系列データから残差だけを抽出すると上図のようなグラフになります。

それでは具体例を使って時系列データをトレンド、季節性、残差に分解してみましょう。なおこの記事では移動平均を用いた分解方法を解説します。

この後色々計算をしますが、実際にデータを分析する際はパソコンが全部計算してくれるので別に自分で一から計算出来る必要はないです。

元データを用意する

今回は上の時系列データを使います。このデータは2022年1月から2023年12月までの24カ月間のデータです。

グラフにすると上図のようになります。

周期を決定する

次にこの時系列データの周期（period）を決めます。第3章で説明したように、この時系列データは3カ月周期であると考えられるので、周期は3カ月と決定します。

トレンドを抽出する

次にトレンドを抽出しましょう。トレンドの抽出には移動平均を用います。簡単に説明すると移動平均とは

範囲をずらしながらデータの平均値を求めること

です。具体例を使って移動平均を求めていきます。今元データの2022年1月、2月、3月のデータ値はそれぞれ1,3,2なので、平均値を計算すると

(2022年1月、2月、3月の平均値)：\(\frac{1+3+2}{3}=2\)

と計算できます。次に元データの2022年2月、3月、4月のデータ値はそれぞれ3,2,2なので、平均値を計算すると

(2022年2月、3月、4月の平均値)：\(\frac{3+2+2}{3}=2.333333…\)

と計算できます。次に元データの2022年3月、4月、5月のデータ値はそれぞれ2,2,4なので、平均値を計算すると

(2022年3月、4月、5月の平均値)：\(\frac{2+2+4}{3}=2.666666…\)

と計算できます。次に元データの2022年4月、5月、6月、…というように、1カ月ずつ範囲をずらして3カ月の平均値を計算していきます。なぜ毎回3カ月の平均値を求めるかと言うと

周期が3カ月だから

です。もし元データの周期が4カ月だと思ったら4カ月の平均値を求めて1カ月ずつずらしていけば良いし、元データの周期が12カ月だと思ったら12カ月の平均値を求めて1カ月ずつずらしていけばOKです。

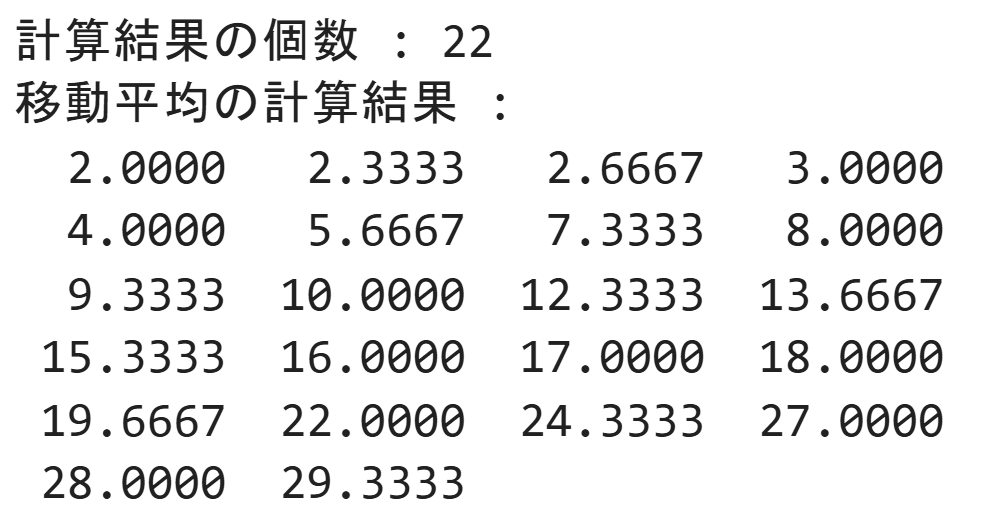
このように2023年10月、11月、12月まで移動平均を計算していくと、上のような計算結果になると思います。グラフにすると下図のようになります。

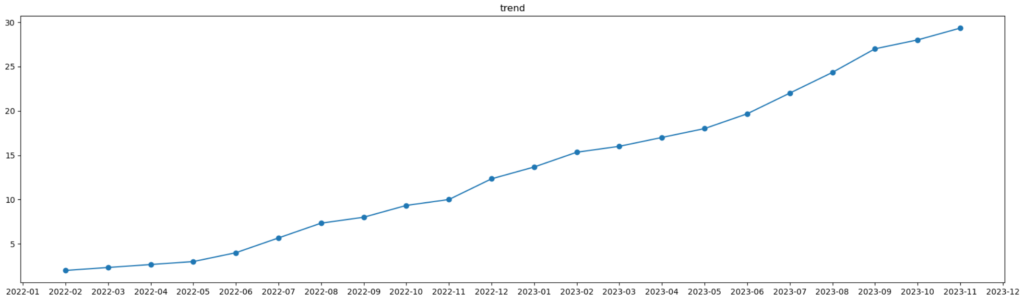
ここで注目すべきなのはトレンドデータの個数が22個しかないということです。これはトレンドデータを求めるために、24個のデータから3個ずつ平均値を計算しているためです。

トレンドデータも24か月分のデータにするために両端のデータ値を補完する必要がありますが、ここでは最小二乗法を使って2022年1月のデータと2023年12月のデータを推定する手法を採用します。

2022年1月のトレンドデータを推定する

2022年1月のトレンドデータを推定しましょう。推定方法の詳細を下記に記します。

それではまず2022年1月のデータの推定に用いるデータとして、2022年1月に最も近い3カ月の

2022年2月のデータ：\((x_1,y_1)=(2,2)\)
2022年3月のデータ：\((x_2,y_2)=(3,\frac{7}{3})\)
2022年4月のデータ：\((x_3,y_3)=(4,\frac{8}{3})\)

を用意します。なお計算を楽にするため小数ではなく分数で表しています。


次に最小二乗法によって線形回帰モデル\(y = ax+b\)の最適パラメータ\(a,b\)を求めます。すなわち

\(L = \sum\limits_{i=1}^{3}(y_i-ax_i-b)^2\)

として、\(L\)を\(a,b\)でそれぞれ偏微分した式が0となるような\(a,b\)を求めます。すなわち

\(\frac{\partial L}{\partial a} = -2 \sum\limits_{i=1}^{3} x_i (y_i-ax_i-b) = 0\)
\(\frac{\partial L}{\partial b} = -2 \sum\limits_{i=1}^{3} (y_i-ax_i-b) = 0\)

上の2つの連立方程式を解きます。この2式をもう少し簡単な式にすると

\(\sum\limits_{i=1}^3x_iy_i=a\sum\limits_{i=1}^3{x_i}^2+b\sum\limits_{i=1}^3x_i\) ー ①
\(\sum\limits_{i=1}^3y_i=a\sum\limits_{i=1}^3x_i+3b\) ー ②

となります。\(x_i,y_i\)に具体的な値を代入すると

\(\sum\limits_{i=1}^3x_i=2+3+4=9\)
\(\sum\limits_{i=1}^3y_i=2+\frac{7}{3}+\frac{8}{3}=7\)
\(\sum\limits_{i=1}^3x_i^2=2^2+3^2+4^2=29\)
\(\sum\limits_{i=1}^3x_iy_i=(2\times2)+(3\times\frac{7}{3})+(4\times\frac{8}{3})=\frac{65}{3}\)

となるので①,②式に代入すると

\(29a+9b=\frac{65}{3}\) ー ①
\(9a+3b=7\) ー ②

となります。これを解くと\(a = \frac{1}{3},b=\frac{4}{3}\)となります。

最後に今求めた線形回帰モデルに\(x=1\)を代入して2022年1月のトレンドデータの値を推定します。\(x=1\)を代入すると

\(y=ax+b=\frac{1}{3}\times1+\frac{4}{3}=\frac{5}{3}=1.666666…\)

となり、2022年1月のトレンドデータの値は\(\frac{5}{3}=1.666666…\)と推定できました。

2023年12月のトレンドデータを推定する

次に2023年12月のトレンドデータを推定しましょう。推定方法の詳細を下記に記します。

それではまず2023年12月のデータの推定に用いるデータとして、2023年12月に近い3カ月の

2023年8月のデータ：\((x_1,y_1)=(20,\frac{73}{3})\)
2023年9月のデータ：\((x_2,y_2)=(21,27)\)
2023年10月のデータ：\((x_3,y_3)=(22,28)\)

を用意します。なお計算を楽にするため小数ではなく分数で表しています。

次に最小二乗法によって線形回帰モデル\(y = ax+b\)の最適パラメータ\(a,b\)を求めます。先ほどと同じで以下の2式

\(\sum\limits_{i=1}^3x_iy_i=a\sum\limits_{i=1}^3{x_i}^2+b\sum\limits_{i=1}^3x_i\) ー ①
\(\sum\limits_{i=1}^3y_i=a\sum\limits_{i=1}^3x_i+3b\) ー ②

を解きます。\(x_i,y_i\)に具体的な値を代入すると

\(\sum\limits_{i=1}^3x_i=20+21+22=63\)
\(\sum\limits_{i=1}^3y_i=\frac{73}{3}+27+28=\frac{238}{3}\)
\(\sum\limits_{i=1}^3x_i^2=20^2+21^2+22^2=1325\)
\(\sum\limits_{i=1}^3x_iy_i=(20\times\frac{73}{3})+(21\times27)+(22\times28)=\frac{5009}{3}\)

となるので①,②式に代入すると

\(1325a+63b=\frac{5009}{3}\) ー ①
\(63a+3b=\frac{238}{3}\) ー ②

となります。これを解くと\(a = \frac{11}{6},b=-\frac{217}{18}\)となります。

最後に今求めた線形回帰モデルに\(x=24\)を代入して2023年12月のトレンドデータの値を推定します。\(x=24\)を代入すると

\(y=ax+b=\frac{11}{6}\times24-\frac{217}{18}=\frac{217}{18}=31.944444…\)

となり、2023年12月のトレンドデータの値は\(\frac{217}{18}=31.944444…\)と推定できました。

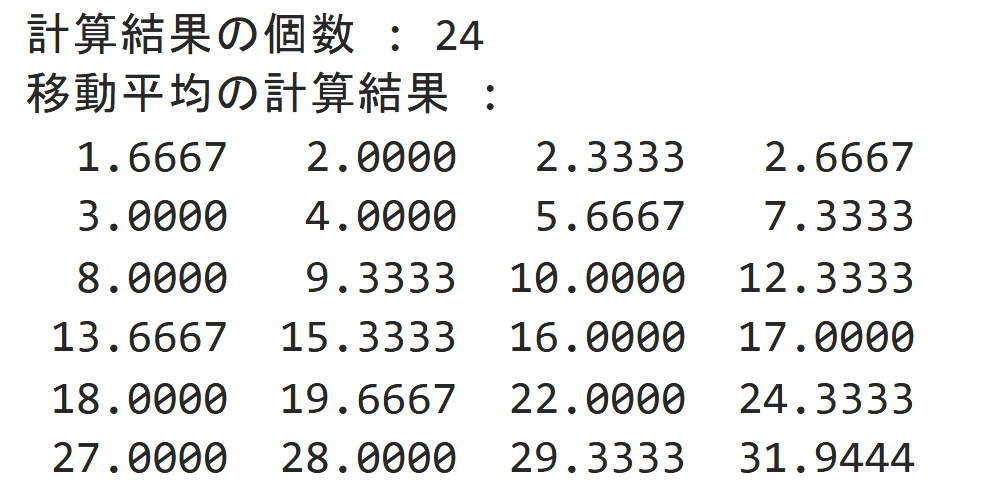
ということでトレンドデータが上のように計算できました。これをグラフにすると下図のようになります。

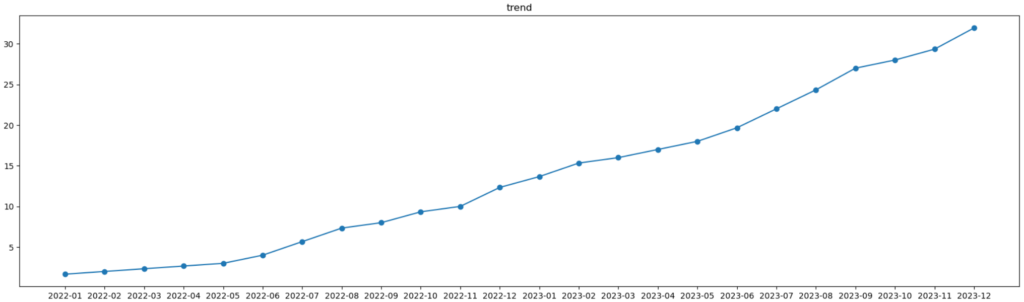
季節性を抽出する

それでは次に季節性を抽出しましょう。季節性を抽出するためには、まず元データの値からトレンドデータの値を引き算する必要があります。例えば2022年1月の元データ値は1、トレンドデータ値は1.666666…なので元データ値からトレンドデータ値を引き算すると

\(1-1.666666…=-0.666666\)

と計算できます。これを全ての月で計算すると以下のような計算結果が得られると思います。

そして次にこのデータから、このデータの平均値を引き算します。上のデータの平均値を計算すると

\(\frac{-0.6666…+1+…+0.6666…-2.9444…}{24}=-0.108796…\)

となります。これをこのデータの各値から引き算しましょう。引き算すると下のような計算結果が得られると思います。

グラフにすると下図のようになります。

続いてこのデータを周期でグループ分けして、各グループの平均値を求めます。今周期は3カ月なので、上のデータを3グループに分類します。

グループ1：2022年1月、4月、7月、10月、2023年1月、4月、7月、10月
グループ2：2022年2月、5月、8月、11月、2023年2月、5月、8月、11月
グループ3：2022年3月、6月、9月、12月、2023年3月、6月、9月、12月

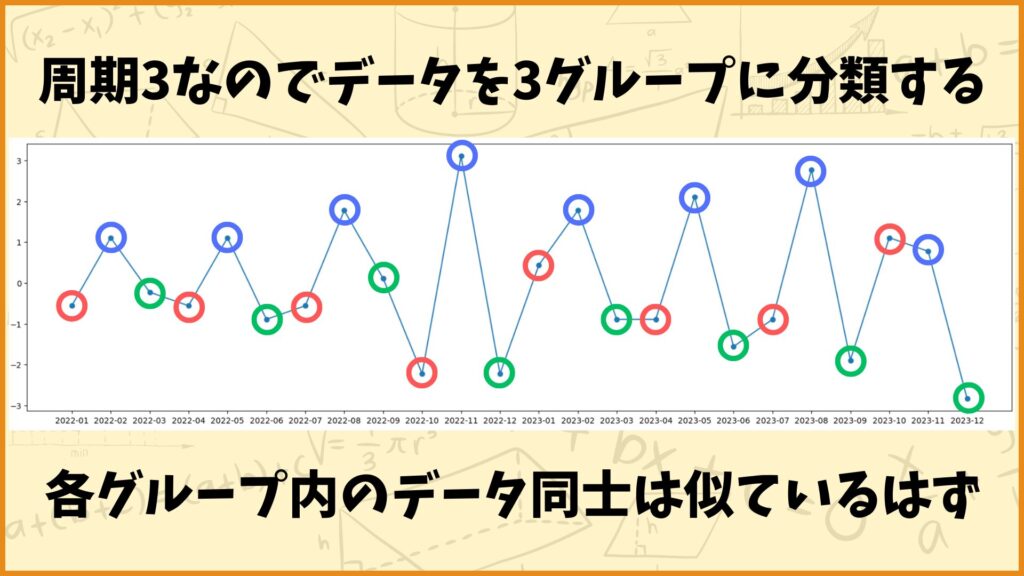
上図を見ると分かるように、同じグループ内のデータ同士は似ているはずです。例えばグループ2は値が大きい傾向があります。

各グループに対して平均値を求めることで、そのグループの傾向が分かります。今回の場合だと3カ月周期ですが、1カ月目は小さな値、2カ月目は大きな値、3カ月目は小さな値という傾向を計算することができます。

それでは実際に計算してみましょう。

グループ1：\(\frac{-0.55787…-0.55787…+…+1.10879…}{8}=-0.51620…\)
グループ2：\(\frac{1.10879…+1.10879…+…+0.77546…}{8}=1.81712…\)
グループ3：\(\frac{-0.22453…-0.89120+…-2.83564…}{8}=-1.30092…\)

このように計算できました。季節性データはこの3つのデータが何回も繰り返されます。今回はこの3カ月周期のデータが24か月分繰り返されるので、上のデータが8回繰り返されます。

以上のことから季節性データは下記のように計算することができました。

グラフにすると下図のようになります。

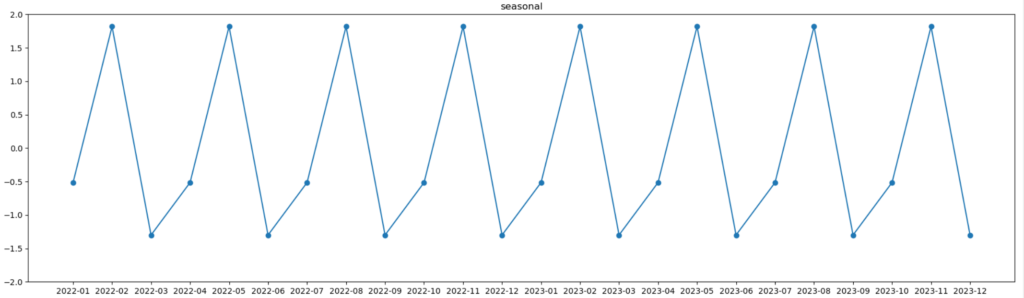
残差を抽出する

残差データの抽出方法は簡単で、元データからトレンドデータと季節性データを引き算すれば良いです。季節性データを計算するところで、既に元データからトレンドデータを引き算していました。

なのでこのデータから下図の季節性データを引き算すれば残差データが手に入ります。

例えば2022年1月の残差データ値は

\(-0.66666…+0.51620…=-0.15046…\)

と計算できます。他の月も同じように計算すると下のような結果が得られると思います。

グラフにすると下図のようになります。

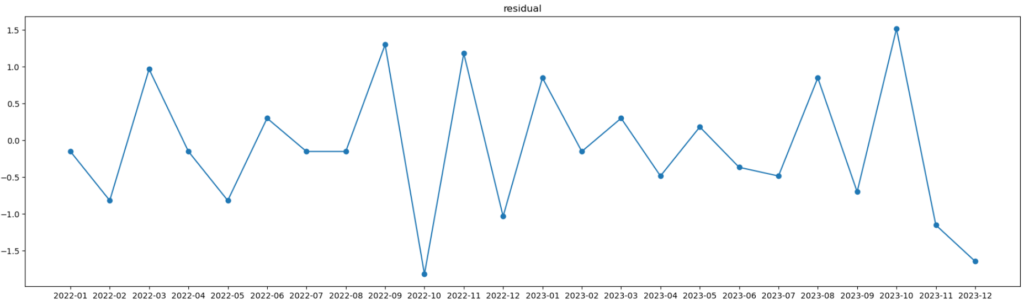
まとめ

ということで最終的に以下のように元データをトレンド、季節性、残差の3つに分解することができました。

元データ

トレンド

季節性

残差

それでは最後にpythonを使って時系列データをトレンド、季節性、残差の3つに分解してみましょう。今回はstatsmodelsライブラリを使います。statsmodelsを使えば時系列データの分解が超簡単にできます。

それでは「事前準備」、「時系列データの準備」、「時系列データの分解」、「分解結果を確認する」の順に説明していきます。

事前準備

## 事前準備
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose

まず最初に今回使用するライブラリやメソッドをインポートします。

matplotlib：pythonでグラフを作成するために使うライブラリ
statsmodels：pythonで時系列データを分解するために使うライブラリ
seasonal_decompose：statsmodelのメソッドの1つ。トレンド、季節性、残差の3つに分解するために使う。

各ライブラリ・メソッドの説明は上記の通りです。

時系列データの準備

## 時系列データの準備
data = [1,3,2,2,4,3,5,9,8,7,13,10,14,17,15,16,20,18,21,27,25,29,30,29]

# 日付のリストを作成
date_list = []
for year in range(2022, 2024):
  for month in range(1, 13):
    date_list.append(f"{year:04}-{month:02}")

続いて時系列データの準備をしていきます。

2行目で時系列データをリスト形式で用意しています。データの個数は24個にしました。

5行目～8行目で日付のリストを用意しています。日付は2022年1月～2023年12月の24カ月にしました。時系列データの分解自体に日付データは使いませんが、グラフの作成の際に使います。

本題とはあまり関係ないですが、この時系列データの折れ線グラフは下図のようになります。

plt.figure(figsize=(22,6))
plt.plot(date_list, data, marker="o")
plt.show()

時系列データの分解

## 時系列データの分解
period = 3
result = seasonal_decompose(data, model="additive", period=period, extrapolate_trend="freq")

それでは今回の本題である、時系列データの分解をしていきます。なんとseasonal_decomposeメソッドを使えばたったこれだけのコードで実装できちゃいます。

2行目で周期を設定しています。今回は3カ月周期なので「period = 3」としています。

3行目で時系列データの分解をしています。引数は左から順に

data：分解したいデータを指定する。
model：モデルを指定する。「additive」とすることで加法モデル（この記事で紹介した方法）に設定できる。
period：周期を指定する。
extrapolate_trend：外挿の設定をする。「freq」とすることで周期分（今回だと3つ分）を使って端のデータを推定する。

となっています。分解結果は「result」としておきました。この後結果を確認するときにこの「result」を使います。

分解結果を確認する

##結果の表示
print("---トレンド---")
print(result.trend)

print("---季節性---")
print(result.seasonal)

print("---残差---")
print(result.resid)

それでは分解結果を確認してみましょう。

2～3行目でトレンドを表示しています。トレンドは「.trend」で取り出せます。
5～6行目で季節性を表示しています。季節性は「.seasonal」で取り出せます。
8～9行目で残差を表示しています。残差は「.resid」で取り出せます。

これを見ると第4章で計算した値と同じになっていますね。自分で計算できて嬉しいと思う一方で、あんなに大変な計算をコンピュータなら一瞬で出来てしまうことの偉大さを感じます…

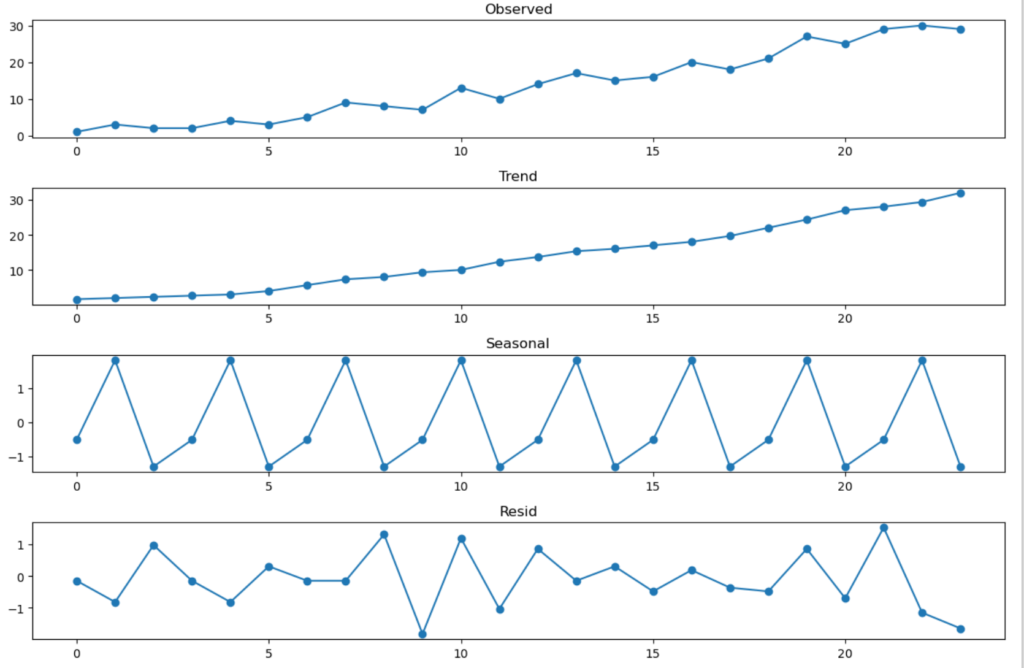
数字だけじゃよく分からないのでグラフにしてみましょう。

# グラフ描画
plt.figure(figsize=(12, 8)) # グラフのサイズ調整

# 元データのプロット
plt.subplot(4, 1, 1)
plt.plot(result.observed, marker = "o")
plt.title('Observed')

# トレンド成分のプロット
plt.subplot(4, 1, 2)
plt.plot(result.trend, marker = "o")
plt.title('Trend')

# 季節成分のプロット
plt.subplot(4, 1, 3)
plt.plot(result.seasonal, marker = "o")
plt.title('Seasonal')

# 残差成分のプロット
plt.subplot(4, 1, 4)
plt.plot(result.resid, marker = "o")
plt.title('Resid')

# グラフ間の余白調整
plt.tight_layout() 

# 表示
plt.show() 

別の時系列データを使って分解してみる

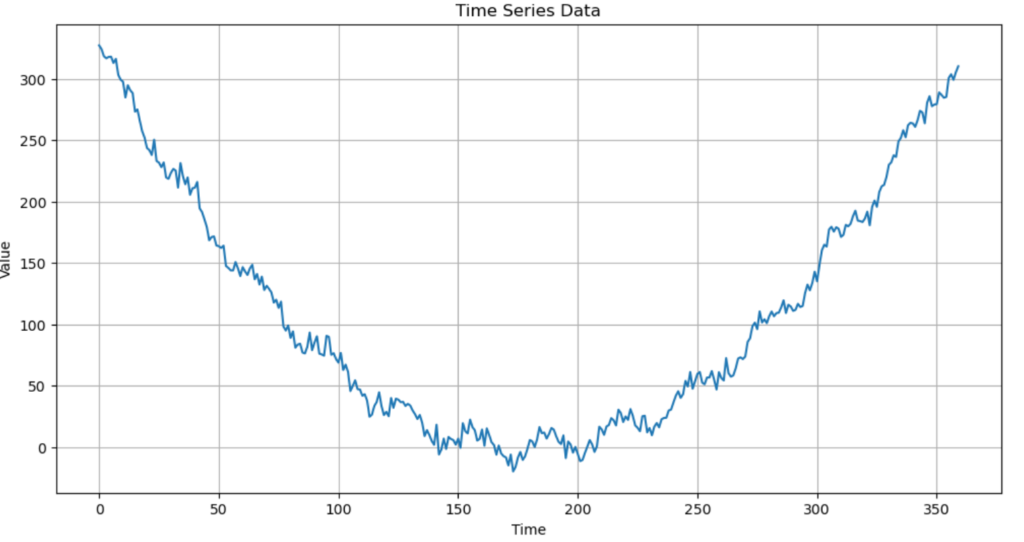
別の時系列データを使って分解してみました。時系列データの作成以外の手順は同じなので説明は省略します。

import numpy as np
import matplotlib.pyplot as plt

# パラメータ設定
n_samples = 360  # データ点数
period = 30      # 周期（日数）
noise_scale = 5   # ノイズの大きさ

# 時間軸の作成
time = np.arange(n_samples)

# トレンド成分（二次関数）
trend = 0.01 * (time - n_samples / 2)**2 

# 季節成分（sin関数）
seasonal = 10 * np.sin(2 * np.pi * time / period) 

# ホワイトノイズ
noise = np.random.normal(scale=noise_scale, size=n_samples)

# 時系列データの生成
data = trend + seasonal + noise

# グラフ描画
plt.figure(figsize=(12, 6)) 
plt.plot(data)
plt.title("Time Series Data")
plt.xlabel("Time")
plt.ylabel("Value")
plt.grid(True)
plt.show()

このデータの数は360個で、二次関数をベースにsin関数で30日周期の季節性を加え、最後にホワイトノイズを加えたデータとなっています。そのためトレンドが二次関数、季節性がsin関数となることが予想されます。

それでは実際に分解して結果を確認してみましょう。

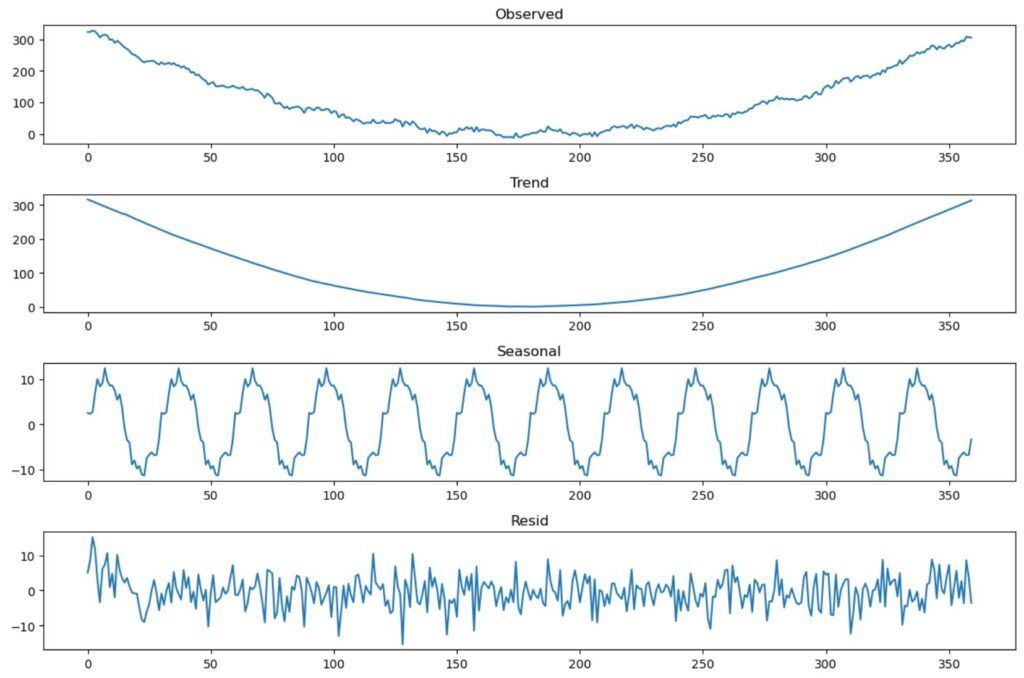
上から順に元データ、トレンド、季節性、残差のグラフとなっています。なお周期は30としています。これを見るとトレンドが二次関数ぽくなっていて、季節性がsin関数ぽくなっていますね。想定通りです。

いかがでしたか。

今回の記事では時系列データの分解について解説しました。

今後もこのようなデータ分析に関する記事を書いていきます！

最後までこの記事を読んでくれてありがとうございました。

参考文献

統計学基礎改訂版 日本統計学会公式認定統計検定2級対応 [ 日本統計学会 ]

created by Rinker

¥2,420 (2024/09/19 09:38:35時点 楽天市場調べ-詳細)

book:17718487

• 楽天市場