- SCIPってなに?
- 無料の最適化ソルバーのCBCだと遅い…
- SCIPってCBCと比べるとどれくらい速いの?
こんにちは!しゅんです!
普段最適化問題を解くときはデフォルトのCBCソルバーを使っていたんですが、どうやらSCIPという無償のソルバーが使えるらしいという話を聞きました。
ということでこの記事ではSCIPとCBCでどれくらい計算時間に差が出るのかを調べてみたいと思います!
それではやっていきましょう!
【Udemy講座公開のお知らせ】
このたびUdemyで数理最適化の講座を公開しました!この講座は「数理最適化を勉強してみたいけど数式が多くて難しい…」という方向けに、どうやって最適化問題を定式化すれば良いかを優しく丁寧に解説しています!
SCIPってなに?
SCIPはドイツのZuse Institute Berlinという所が提供している最適化ソルバーです。SCIPは無料で利用することができるソルバーで、線形計画問題、混合整数計画問題、そして非線形の混合整数計画問題も解けるそうです。
そしてSCIPは無料で利用できるのに結構計算が速いそうです。無料のソルバーと言うとまずCBCが思い浮かぶと思いますが、CBCよりも全然速いらしいです。
ということでこの記事では本当にCBCより速いのかを実験してみたいと思います!
SCIPを利用する方法
ぼくはWindowsを使っているのでWindowsで利用する方法を紹介します。またSCIPはPulpが対応しているソルバーなので、最適化問題のモデリングはPulpで書いて、ソルバーをSCIPに指定する方法を紹介します。
SCIPはPulpだけじゃなくてPySCIPOptというSCIP独自のPythonインターフェースも用意されているそうです。
まずSCIPの公式サイト (https://scipopt.org) に移動します。

Downloadの所に移動して「SCIPOptSuite-9.2.1-win64.exe」をクリックしてダウンロードします。
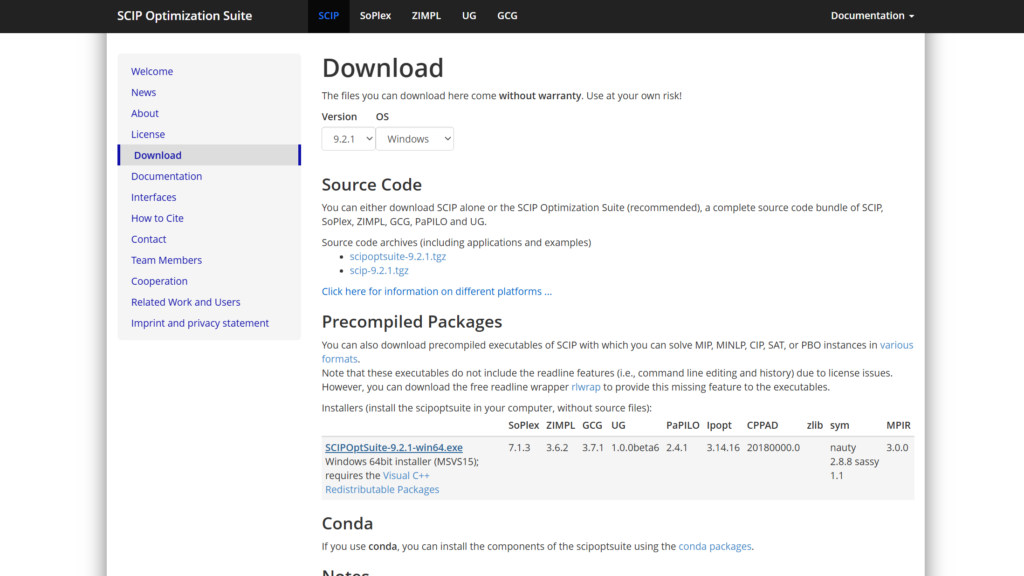
今ダウンロードした「SCIPOptSuite-9.2.1-win64.exe」をクリックしてインストールします。インストールするときにPATH環境変数を設定しておきます。

これでSCIPが使えるようになります。あとはPulpで最適化問題を記述してソルバーをSCIPに設定すればOKです。それでは適当に最適化問題を記述していきます。
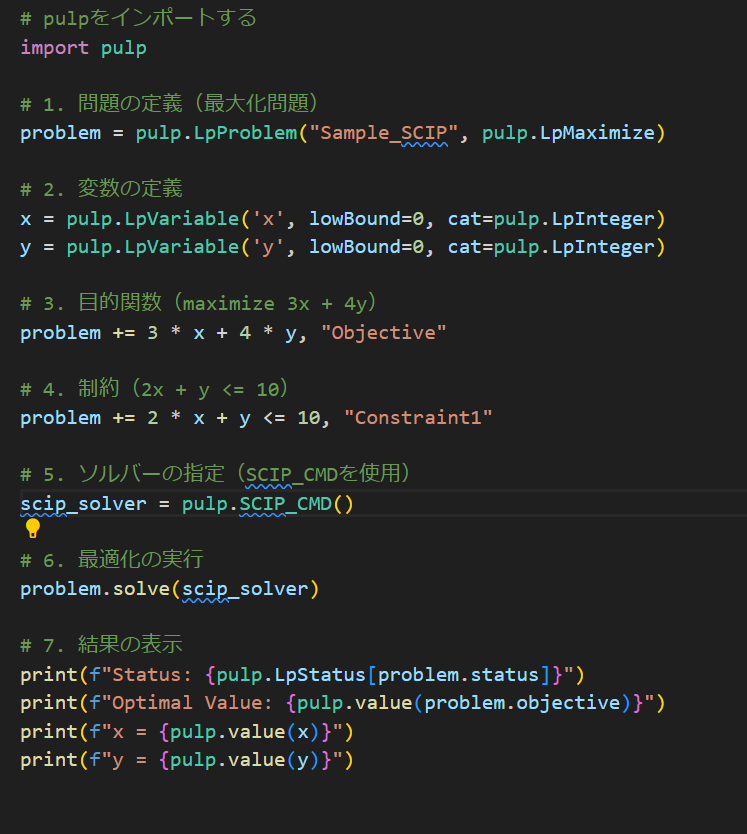
# pulpをインポートする
import pulp
# 1. 問題の定義(最大化問題)
problem = pulp.LpProblem("Sample_SCIP", pulp.LpMaximize)
# 2. 変数の定義
x = pulp.LpVariable('x', lowBound=0, cat=pulp.LpInteger)
y = pulp.LpVariable('y', lowBound=0, cat=pulp.LpInteger)
# 3. 目的関数(maximize 3x + 4y)
problem += 3 * x + 4 * y, "Objective"
# 4. 制約(2x + y <= 10)
problem += 2 * x + y <= 10, "Constraint1"
# 5. ソルバーの指定(SCIP_CMDを使用)
scip_solver = pulp.SCIP_CMD()
# 6. 最適化の実行
problem.solve(scip_solver)
# 7. 結果の表示
print(f"Status: {pulp.LpStatus[problem.status]}")
print(f"Optimal Value: {pulp.value(problem.objective)}")
print(f"x = {pulp.value(x)}")
print(f"y = {pulp.value(y)}")ソルバーの指定の所で「.SCIP_CMD()」と設定することでソルバーをSCIPに指定できます。このプログラムを実行するとSCIPを使った結果が得られると思います。

プログラムを実行したときに上図のようなエラーが出力されたらおそらくPATH環境変数が設定できていないんだと思います。そういうときは「scip.exe」が置いてあるディレクトリを探してPATH環境変数を設定してください。
上手くいったら下図のようなログが出力されると思います。
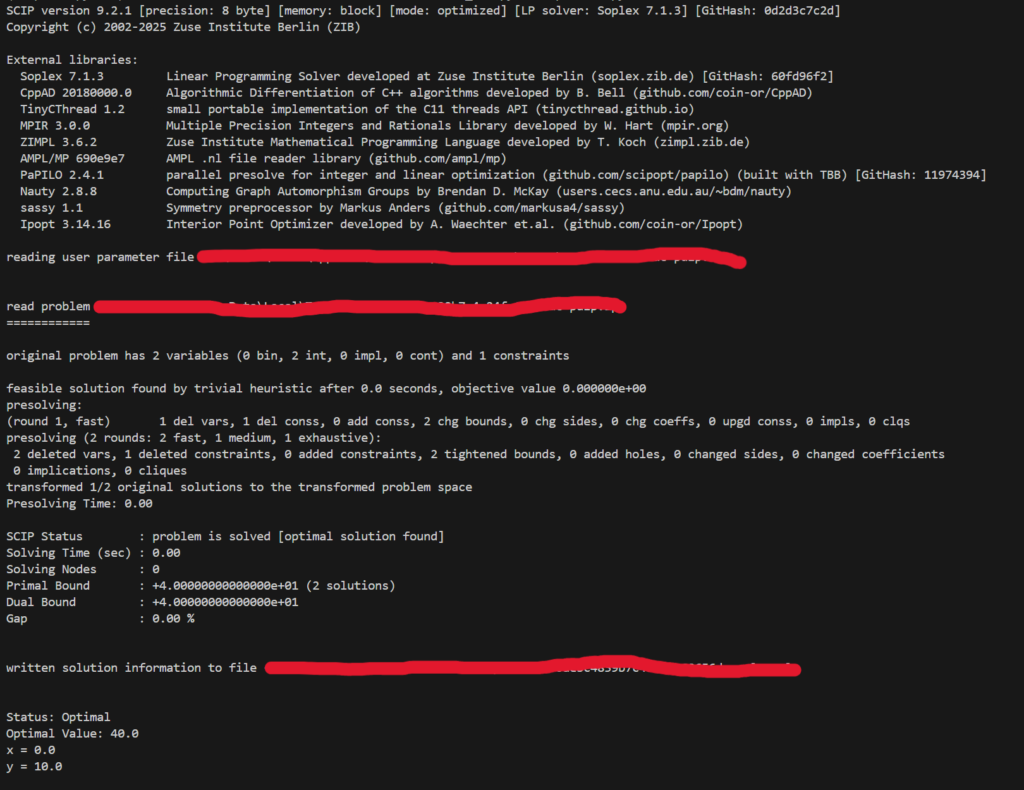
ということでこのようなログが出力されたら無事SCIPを利用することができたことになります。
SCIPとCBCを比較してみよう!(ベンチマーク問題での比較)
ここからが本題です。SCIPとCBCでどれくらい計算時間が変わるのかを調べてみましょう。自分で作った問題でSCIPとCBCの計算時間を比較をしたいんですが、その前にまずベンチマーク問題での比較を見てみましょう。
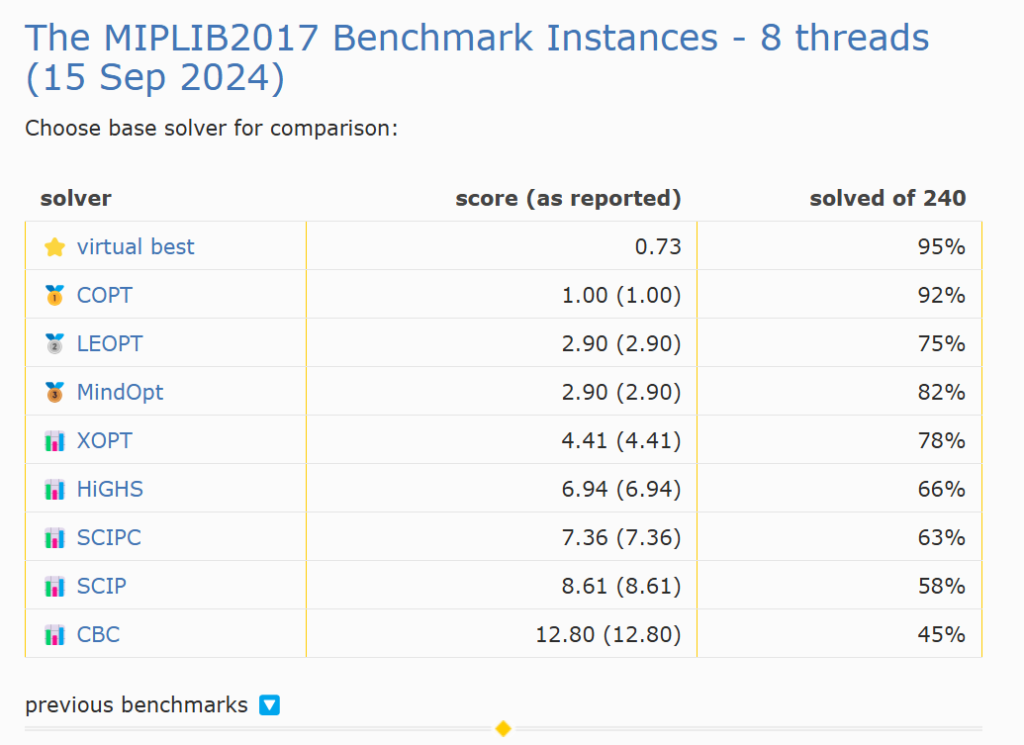
上図はMIPLIBのベンチマーク問題での性能比較をした結果のようですが、これを見ると確かにCBCよりSCIPの方が計算時間が速いようです。
一番上のCOPTというソルバーの計算時間を1としたときに何倍の時間がかかるのかというスコアを出しているのだと思われます。
SCIP:約8.61倍の時間を要し、全体の58%が解けた
CBC:約12.80倍の時間を要し、全体の45%が解けた
という結果になりました。SCIPはCBCより速いとはいえまだまだCOPTには敵わないことが分かります。ちなみにCOPTは有償ソルバーです。
SCIPとCBCを比較してみよう!(自分で作った問題での比較)
巡回セールスマン問題の詳しい話は過去の記事で詳しく解説しているのでこの記事では説明を省略します。
本題ではないですがディレクトリ構造は下図のような感じでimageフォルダに出力解の図を保存するようにしました。
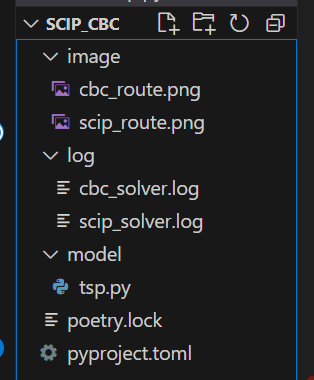
計算実験に用いたコードは下記の通りです。ちょっと長いので気になる人だけ見てみてください。
import random
import math
import os
import pulp
import matplotlib.pyplot as plt
def generate_tsp_instance(num_cities, seed=None):
"""
指定した都市数のTSPインスタンスを生成する関数。
ランダムな座標を生成し、各都市間のユークリッド距離を計算する。
Args:
num_cities (int): 都市の数。
seed (int, optional): 乱数シード。指定すれば再現性が得られる。
Returns:
cities (list): 都市番号のリスト(例: [0, 1, ..., num_cities-1])
dist (dict): 各ペア (i, j) についての距離 { (i,j): distance }(i != j)
coords (dict): 各都市の座標 { i: (x, y) }
"""
if seed is not None:
random.seed(seed)
cities = list(range(num_cities))
# 都市の座標を [0, 100] の範囲でランダムに生成
coords = {i: (random.uniform(0, 100), random.uniform(0, 100)) for i in cities}
# 各都市間のユークリッド距離を計算(i != j のみ)
dist = {}
for i in cities:
for j in cities:
if i != j:
xi, yi = coords[i]
xj, yj = coords[j]
distance = math.sqrt((xi - xj) ** 2 + (yi - yj) ** 2)
dist[(i, j)] = distance
return cities, dist, coords
def solve_tsp_instance(cities, dist, timelimit=300, solver="cbc"):
"""
与えられたTSPインスタンスをPuLPで解く関数。
Miller–Tucker–Zemlin (MTZ) 制約を用いてサブツアー除去を行う定式化を行う。
Args:
cities (list): 都市番号のリスト。
dist (dict): 各ペア (i,j) の距離 { (i,j): distance }。
timelimit (int, optional): ソルバーのタイムリミット(秒)。
solver (str, optional): 使用するソルバー。 "cbc" または "scip" を指定。
Returns:
problem (pulp.LpProblem): 解が格納されたPuLP問題オブジェクト。
x (dict): 経路決定変数の辞書(x[i][j] の値が1なら都市 i から都市 j へ移動)
"""
n = len(cities)
problem = pulp.LpProblem("TSP", pulp.LpMinimize)
# 変数 x[i][j]: 都市 i から都市 j への経路(0/1変数)
x = pulp.LpVariable.dicts("x", (cities, cities), cat=pulp.LpBinary)
# 補助変数 u[i]:MTZ制約用(各都市の訪問順序を表す)
u = pulp.LpVariable.dicts("u", cities, lowBound=0, upBound=n-1, cat=pulp.LpContinuous)
# 目的関数: 総移動距離の最小化
problem += pulp.lpSum(dist[(i, j)] * x[i][j]
for i in cities for j in cities if i != j), "Total_Distance"
# 各都市からは必ず1本の辺が出る
for i in cities:
problem += pulp.lpSum(x[i][j] for j in cities if i != j) == 1, f"Out_{i}"
# 各都市へは必ず1本の辺が入る
for j in cities:
problem += pulp.lpSum(x[i][j] for i in cities if i != j) == 1, f"In_{j}"
# サブツアー除去のためのMTZ制約(都市0以外の各 i,j に対して)
for i in cities:
for j in cities:
if i != j and i != 0 and j != 0:
problem += u[i] - u[j] + n * x[i][j] <= n - 1, f"MTZ_{i}_{j}"
# ログファイル名の設定。既存のファイルがあれば削除して上書きする
log_file = f"log\{solver}_solver.log"
if os.path.exists(log_file):
os.remove(log_file)
# ソルバーの選択(cbcまたはscip)
if solver == "cbc":
pulp_solver = pulp.PULP_CBC_CMD(timeLimit=timelimit, msg=False, logPath=log_file)
else:
pulp_solver = pulp.SCIP_CMD(timeLimit=timelimit, msg=False, logPath=log_file)
# 最適化実行
problem.solve(pulp_solver)
return problem, x
def extract_route(cities, x_vars):
"""
x_vars の値から、都市0を起点とした巡回ルートを抽出する関数。
Args:
cities (list): 都市番号のリスト。
x_vars (dict): x[i][j] の辞書(最適化解の値を持つ)
Returns:
route (list): 巡回ルート(例: [0, 3, 1, 2, 0])
"""
route = [cities[0]]
current = cities[0]
while True:
next_city = None
for j in cities:
if current != j and pulp.value(x_vars[current][j]) > 0.5:
next_city = j
break
if next_city is None or next_city == route[0]:
break
route.append(next_city)
current = next_city
# 巡回ルートなので最終的に起点に戻す
route.append(route[0])
return route
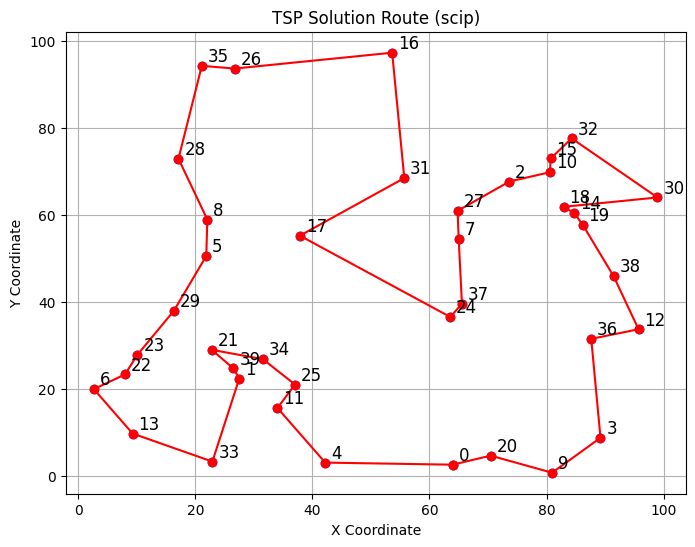
def plot_tsp_solution(cities, coords, x_vars, solver):
"""
抽出したTSP解のルートをmatplotlibで描画する関数。
Args:
cities (list): 都市番号のリスト。
coords (dict): 各都市の座標 { i: (x, y) }。
x_vars (dict): x[i][j] の最適解の値を持つ辞書。
solver (str): 使用するソルバー。 "cbc" または "scip" を指定。
"""
route = extract_route(cities, x_vars)
# 各都市の座標リストを作成
route_x = [coords[city][0] for city in route]
route_y = [coords[city][1] for city in route]
plt.figure(figsize=(8, 6))
# 都市を散布図でプロットし、都市番号も表示
for city in cities:
plt.scatter(coords[city][0], coords[city][1], color='blue')
plt.text(coords[city][0] + 1, coords[city][1] + 1, str(city), fontsize=12)
# ルートを赤い線で描画
plt.plot(route_x, route_y, color='red', linestyle='-', marker='o')
plt.title(f"TSP Solution Route ({solver})")
plt.xlabel("X Coordinate")
plt.ylabel("Y Coordinate")
plt.grid(True)
plt.savefig(f"image\{solver}_route.png", bbox_inches='tight')
plt.close()
# 例: 都市数を入力してインスタンスを生成し、最適化実行および解の描画を行う
num_cities = 20 # 例として20都市
solver = "cbc"
cities, dist, coords = generate_tsp_instance(num_cities, seed=42)
problem, x_vars = solve_tsp_instance(cities, dist, timelimit=300, solver=solver)
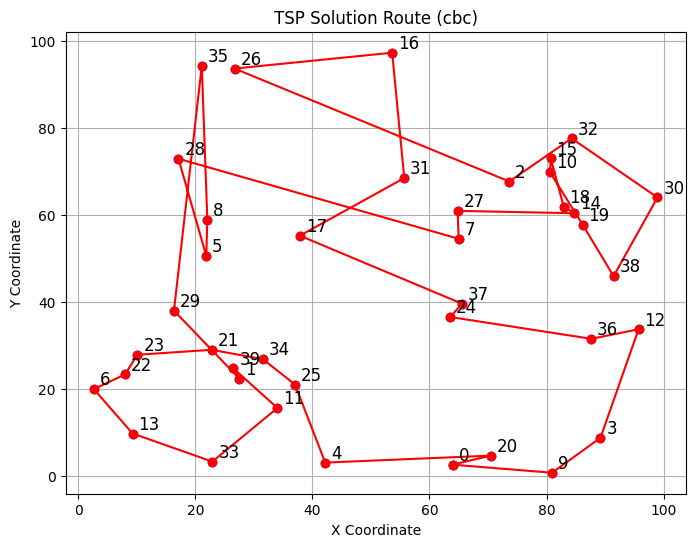
plot_tsp_solution(cities, coords, x_vars, solver=solver)制限時間5分で、今回は20地点、30地点、40地点の3つの問題例をCBCとSCIPで解いてみたいと思います。
| 問題例 | CBC | SCIP |
|---|---|---|
| 20地点 | 5.63秒 | 0.00秒 |
| 30地点 | 22.90秒 | 12.00秒 |
| 40地点 | 300秒(タイムリミット) | 95.00秒 |
ということで上の表のような結果になりました。これを見ると全然SCIPの方が計算が速いですね。40地点の問題例だとCBCはそもそも5分以内に最適解を見つけることができませんでしたが、SCIPは95秒で最適解を見つけることができました。
おわりに
いかがでしたか。
今回の記事では最適化ソルバーのSCIPについて解説していきました。
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。




