- SCIPを使いたい…
- PySCIPOptを使ってみたい…
- CBCよりも早い無料のソルバーを使いたい…
こんにちは!しゅんです!
以前数理最適化ソルバーのSCIPを紹介しましたが、そのときはPuLPでモデリングを行いました。しかしSCIPは専用のpythonインターフェースであるPySCIPOptというものがあります。
ということでこの記事ではPySCIPOptを使って問題を解いていきたいと思います。
\\ 前回の記事はこちら! //
それではやっていきましょう!
【Udemy講座公開のお知らせ】
このたびUdemyで数理最適化の講座を公開しました!この講座は「数理最適化を勉強してみたいけど数式が多くて難しい…」という方向けに、どうやって最適化問題を定式化すれば良いかを優しく丁寧に解説しています!
SCIPってなに?
SCIPはドイツのZuse Institute Berlinという所が開発している数理最適化ソルバーです。SCIPは無料で利用することができるソルバーで、線形計画問題、混合整数計画問題、そして非線形の混合整数計画問題も解けるそうです。
そしてSCIPは無料で利用できるのに結構計算が速いそうです。無料のソルバーと言うとまずCBCが思い浮かぶと思いますが、CBCよりも全然速いらしいです。
前回の記事でSCIPとCBCの比較をしてみましたが、やはりSCIPの方が速かったです。
\\ 前回の記事はこちら! //
PySCIPOptを使ってみよう!
前回の記事でSCIPの利用方法については紹介しているのでそれを参考にしてみてください。この記事ではPySCIPOptを使って数理最適化問題をモデリングする方法にフォーカスして紹介します。
pyscipoptのバージョンは5.4.1です。
モデリングに使用する構文を紹介する
それではまず最初にモデリングに使用する構文を紹介したいと思います。基本的な操作である
・モデルの作成
・変数の作成
・目的関数の作成
・制約条件の作成
・問題を解く
・最適解、最適値の取得
・時間制限の設定
のやり方について1つずつ紹介します。
モデルの作成
# モデルの作成
model = pyscipopt.Model("あいうえお")最適化問題をモデリングするためにはまずモデルを作成する必要があります。イメージとしては箱を作って、その中に変数とか目的関数とかを入れていくみたいな感じです。
pyscipoptでは「pyscipopt.Model()」でモデル(箱)を作成することができます。モデルには「model」という名前を付けました。
このモデル(箱)には名前を付けることができます。上の例では「あいうえお」って名前にしていますが、ここはどんな問題を解くかによって変えましょう。
変数の作成
# 変数の作成
x = model.addVar(vtype="C", name="x")次に変数を作成します。変数の作成は「.addVar()」で行うことができます。引数は
・vtype:変数の種類の設定(”C”:連続変数、”I”:整数変数、”B”:0-1変数)
・name:変数の名前
をそれぞれ表しています。上の例だと変数名が「x」で変数の種類が連続変数であることを表しています。例えば変数を0以上5以下にしたいときは
# 変数の作成
x = model.addVar(vtype="C", name="x", lb=0, ub=5)と書きます。もし \(x_{ij}\) みたいに変数をたくさん設定したいときは
n = 100
x = {}
for i in range(n):
for j in range(n):
x[i,j] = model.addVar(vtype="BINARY", name=f"x_{i}_{j}")みたいな感じで設定できます。ちなみに変数の種類の設定はC,I,Bの代わりに「CONTINUOUS」、「INTEGER」、「BINARY」を使ってもOKです。
目的関数の作成
# 目的関数
model.setObjective(x + 2*y - 3*z, sense = "maximize")
目的関数は「.setObjective()」で設定することができます。引数は左から順に最適化したい目的関数、最大化か最小化かを表しています。
上の例では「maximize」としているので最大化問題に設定しています。もし最小化問題にしたかったら「minimize」とすればOKです。
もし \(\sum\limits_{i \in I}c_ix_i\) みたいにシグマを使って目的関数を作成したいときは
# 目的関数
model.setObjective(quicksum(c[i]*x[i] for i in I, sense = "minimize")という感じで「quicksum()」を使って実装することができます。
制約条件の作成
# 制約条件
model.addCons(x + 2*y <= 3)制約条件は「.addCons()」を使って設定することができます。上の例は \(x+2y\leq 3\) という制約を設定しています。
もし \(w_{i}x_{i} \leq K\)のようにシグマを使って制約条件を設定したいときは
# 制約条件
model.addCons(quicksum(w[i]*x[i] for i in I) <= K)という感じで「quicksum」を使って実装できます。
問題を解く
# 問題を解く
model.optimize()問題を解くときは「.optimize()」を使います。
最適解、最適値の取得
# 解の状態(optimalなら最適値が得られている)
model.getStatus()
# 最適解
model.getVal(x)
# 最適値
model.getObjVal()得られた解が最適解かどうかを見るには「.getStatus()」を使えばOKです。もし返り値が「optimal」なら最適解が得られています。
最適解は「.getVal()」で得られます。また最適値は「.getObjVal()」で得られます。
時間制限の設定
# 時間制限の設定
model.setRealParam('limits/time', 300)時間制限の設定は上のコードで実装できます。上の例だと300秒で計算を中断します。
簡単な線形計画問題をモデリングしてみよう!
目的関数(最大化):
\(3x+4y\)
制約条件
\(x+2y \leq 3\)
\(5x+3y \leq 4\)
\(x \geq 0\)
\(y \geq 0\)
それでは今紹介した構文を使って上の問題をPySCIPOptでモデリングして解いてみたいと思います。
# 事前準備
import pyscipopt
# 簡単な線形計画問題を解く関数の実装
def solve_easy_lp():
# モデルの作成
model = pyscipopt.Model("easy_lp")
# 変数の作成
x = model.addVar(vtype="C", name = "x", lb=0)
y = model.addVar(vtype="C", name = "y", lb=0)
# 目的関数:価値の最大化
model.setObjective(3*x + 4*y, sense = "maximize")
# 1つ目の制約条件
model.addCons(x + 2*y <= 3)
# 2つ目の制約条件
model.addCons(4*x + y <= 4)
# 問題を解く
model.optimize()
# 結果の取得
if model.getStatus() == "optimal":
x_val = model.getVal(x)
y_val = model.getVal(y)
obj_val = model.getObjVal()
return x_val, y_val, obj_val
# 計算を実行する
x_val, y_val, obj_val = solve_easy_lp()
# 最適解を表示する
print(f"最適値 : {obj_val}")
print(f"x : {x_val}")
print(f"y : {y_val}")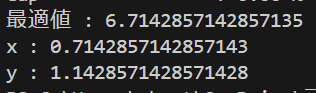
この画像は上のプログラムで最大化問題を解いた結果です。解の状態が「optimal」だったら最適解と最適値を返すように設定しています。
ちゃんと最適化を実行できましたね。
ナップサック問題をモデリングしてみよう!
パラメータ:
\(w_i\) : アイテム \(i\) の重量
\(v_i\) : アイテム \(i\) の価値
\(K\) : ナップサックの容量
変数:
\(x_{i}\) : アイテム \(i\) を持っていくなら1を取る0-1変数
目的関数(最大化):
\(\sum\limits_{i=1}^n v_{i} x_{i}\)
制約条件
\(\sum\limits_{i \in S} w_{i} x_{i} \leq K\)
\(x_{i} \in \{0,1\} \;\;\;\; (i =1,2,…,n)\)
ナップサック問題を整数計画問題として定式化する方法は過去の記事で詳しく解説しています。
from pyscipopt import Model, quicksum
def solve_knapsack(values, weights, capacity):
# モデルの作成
model = Model("knapsack")
# アイテムの数
n = len(values)
# 変数の作成(各アイテムを選ぶかどうかの0-1変数)
items = [model.addVar(vtype="BINARY", name=f"item_{i}") for i in range(n)]
# 目的関数:価値の最大化
model.setObjective(quicksum(values[i] * items[i] for i in range(n)), "maximize")
# 制約条件:重量制限
model.addCons(quicksum(weights[i] * items[i] for i in range(n)) <= capacity)
# 問題を解く
model.optimize()
# 結果の取得
if model.getStatus() == "optimal":
selected_items = [i for i in range(n) if model.getVal(items[i]) > 0.5]
total_value = sum(values[i] for i in selected_items)
total_weight = sum(weights[i] for i in selected_items)
return {
"status": "optimal",
"selected_items": selected_items,
"total_value": total_value,
"total_weight": total_weight,
"objective_value": model.getObjVal()
}
else:
return {"status": model.getStatus(), "selected_items": [], "total_value": 0, "total_weight": 0}
# 例題を解く
if __name__ == "__main__":
# アイテムの価値
values = [60, 100, 120, 80, 30]
# アイテムの重さ
weights = [10, 20, 30, 15, 5]
# ナップサックの容量
capacity = 50
result = solve_knapsack(values, weights, capacity)
print("最適解が"+"見つかりました" if result["status"] == "optimal" else "見つかりませんでした")
print("選択されたアイテム:", result["selected_items"])
print("合計価値:", result["total_value"])
print("合計重量:", result["total_weight"])
print("目的関数値:", result["objective_value"])
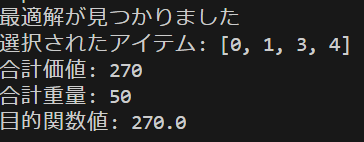
このプログラムを実行すると上のような結果が得られました。
数理モデルの構築部分をもう少し詳しく説明します。
変数
# 変数の作成(各アイテムを選ぶかどうかの0-1変数)
items = [model.addVar(vtype="BINARY", name=f"item_{i}") for i in range(n)]
上の部分では変数 \(x_{i}\)を作成しています。\(x_{i}\) はアイテム \(i\) を選ぶなら1を取る0-1変数です。
目的関数
# 目的関数:価値の最大化
model.setObjective(quicksum(values[i] * items[i] for i in range(n)), "maximize")上の部分では目的関数を設定しています。目的関数は価値 \(v_{i}\) と変数 \(x_{i}\) を使って
\(\sum\limits_{i=1}^n v_{i}x_{i}\)
と表されます。これを「quicksum」を使って表現しています。また目的関数を最大化したいので「sense = “maximize”」としています。
制約条件
# 制約条件:重量制限
model.addCons(quicksum(weights[i] * items[i] for i in range(n)) <= capacity)上の部分では制約条件を設定しています。この制約は重量 \(w_i\) と変数 \(x_i\) と容量制限 \(K\) を使って
\(\sum\limits_{j=1}^n w_ix_i \leq K\)
を表しています。
割当問題をモデリングしてみよう!
パラメータ:
\(c_{ij}\) : 従業員 \(i\) を仕事 \(j\) に割り当てるときのコスト
変数:
\(x_{ij}\) : 従業員 \(i\) を仕事 \(j\) に割り当てるなら1を取る0-1変数
目的関数(最大化):
\(\sum\limits_{i=1}^n\sum\limits_{j=1}^n c_{ij} x_{ij}\)
制約条件
\(\sum\limits_{j = 1} x_{ij} = 1 \;\; (i = 1,2,…,n)\)
\(\sum\limits_{i = 1} x_{ij} = 1 \;\; (j = 1,2,…,n)\)
\(x_{ij} \in \{0,1\} \;\; (i = 1,2,…,n, \; j = 1,2,…,n)\)
割当問題を整数計画問題として定式化する方法は過去の記事で詳しく解説しています。
from pyscipopt import Model, quicksum
def solve_assignment_problem(cost_matrix):
"""
割当問題を解く関数
Parameters:
cost_matrix: n×nの行列。cost_matrix[i][j]はワーカーiがタスクjを実行するコスト
Returns:
最適な割当と総コスト
"""
n = len(cost_matrix) # ワーカー/タスクの数
# モデルの作成
model = Model("assignment_problem")
# 変数の作成:
# x[i][j] = ワーカーiがタスクjに割り当てられる場合は1、そうでなければ0
x = {}
for i in range(n):
for j in range(n):
x[i,j] = model.addVar(vtype="BINARY", name=f"x_{i}_{j}")
# 目的関数: 総コストの最小化
model.setObjective(quicksum(cost_matrix[i][j] * x[i,j] for i in range(n) for j in range(n)), sense = "minimize")
# 制約条件1: 各ワーカーは1つのタスクにのみ割り当てられる
for i in range(n):
model.addCons(quicksum(x[i,j] for j in range(n)) == 1, name=f"worker_{i}")
# 制約条件2: 各タスクは1人のワーカーにのみ割り当てられる
for j in range(n):
model.addCons(quicksum(x[i,j] for i in range(n)) == 1, name=f"task_{j}")
# 問題を解く
model.optimize()
# 結果の取得
if model.getStatus() == "optimal":
# 最適な割当の取得
assignment = {}
for i in range(n):
for j in range(n):
if model.getVal(x[i,j]) > 0.5: # バイナリ変数が1に近い値
assignment[i] = j
total_cost = model.getObjVal()
return {
"status": "optimal",
"assignment": assignment, # ワーカーi -> タスクj
"total_cost": total_cost
}
else:
return {"status": model.getStatus(), "assignment": {}, "total_cost": None}
# 使用例
if __name__ == "__main__":
# コスト行列の例(4人のワーカーと4つのタスク)
cost_matrix = [
[9, 2, 7, 8],
[6, 4, 3, 7],
[5, 8, 1, 8],
[7, 6, 9, 4]
]
result = solve_assignment_problem(cost_matrix)
print("最適解が" + "見つかりました" if result["status"] == "optimal" else "見つかりませんでした")
if result["status"] == "optimal":
print("\n最適な割当:")
for worker, task in result["assignment"].items():
print(f"ワーカー {worker} -> タスク {task} (コスト: {cost_matrix[worker][task]})")
print(f"\n総コスト: {result['total_cost']}")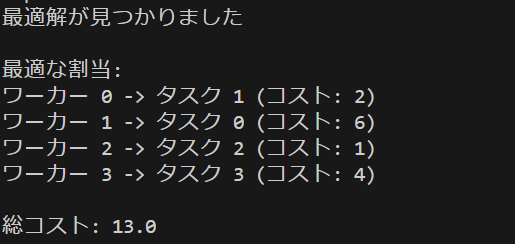
このプログラムを実行すると上のような結果が得られました。
数理モデルの構築部分をもう少し詳しく説明します。
変数
# 変数の作成:
# x[i][j] = ワーカーiがタスクjに割り当てられる場合は1、そうでなければ0
x = {}
for i in range(n):
for j in range(n):
x[i,j] = model.addVar(vtype="BINARY", name=f"x_{i}_{j}")
上の部分では変数 \(x_{ij}\)を作成しています。\(x_{ij}\) は従業員 \(i\) が仕事 \(j\) に割り当てられるなら1を取るような0-1変数です。
目的関数
# 目的関数: 総コストの最小化
model.setObjective(quicksum(cost_matrix[i][j] * x[i,j] for i in range(n) for j in range(n)), sense = "minimize")上の部分では目的関数を設定しています。目的関数はコスト \(c_{ij}\) と変数 \(x_{ij}\) を使って
\(\sum\limits_{i=1}^n\sum\limits_{j=1}^n c_{ij}x_{ij}\)
と表されます。これを「quicksum」を使って表現しています。また目的関数を最小化したいので「sense = “minimize”」としています。
制約条件
# 制約条件1: 各ワーカーは1つのタスクにのみ割り当てられる
for i in range(n):
model.addCons(quicksum(x[i,j] for j in range(n)) == 1, name=f"worker_{i}")
# 制約条件2: 各タスクは1人のワーカーにのみ割り当てられる
for j in range(n):
model.addCons(quicksum(x[i,j] for i in range(n)) == 1, name=f"task_{j}")上の部分では2つの制約条件を設定しています。1つ目の制約は
\(\sum\limits_{j=1}^n x_{ij} = 1 \;\; (i =1,2,…,n)\)
を表しています。また2つ目の制約は
\(\sum\limits_{i=1}^n x_{ij} = 1 \;\; (j = 1,2,…,n)\)
を表しています。
おわりに
今回はPySCIPOptを使って数理最適化の問題をモデリングしていきました!
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。