こんにちは!しゅんです!
今回はクラスタリングにおけるエルボー法について解説していきたいと思います。
クラスタリングによってデータをいくつかのグループに分類します。このとき何個のグループに分類するかを決めるのは結構大変ですよね。そんな時に使えるのがエルボー法です。
ぼくがデータ分析の勉強をしていたときにでてきたので皆さんにもシェアしたいと思います!また今回は説明と一緒にpythonを使ってどんなものか確かめたいと思います。
それでは解説していきましょう!
【Udemy講座公開のお知らせ】
このたびUdemyで数理最適化の講座を公開しました!この講座は「数理最適化を勉強してみたいけど数式が多くて難しい…」という方向けに、どうやって最適化問題を定式化すれば良いかを優しく丁寧に解説しています!
クラスタリングってなに?
ザックリ説明するとクラスタリングは似てるデータを同じグループに分類することです。下の図を見てみましょう。
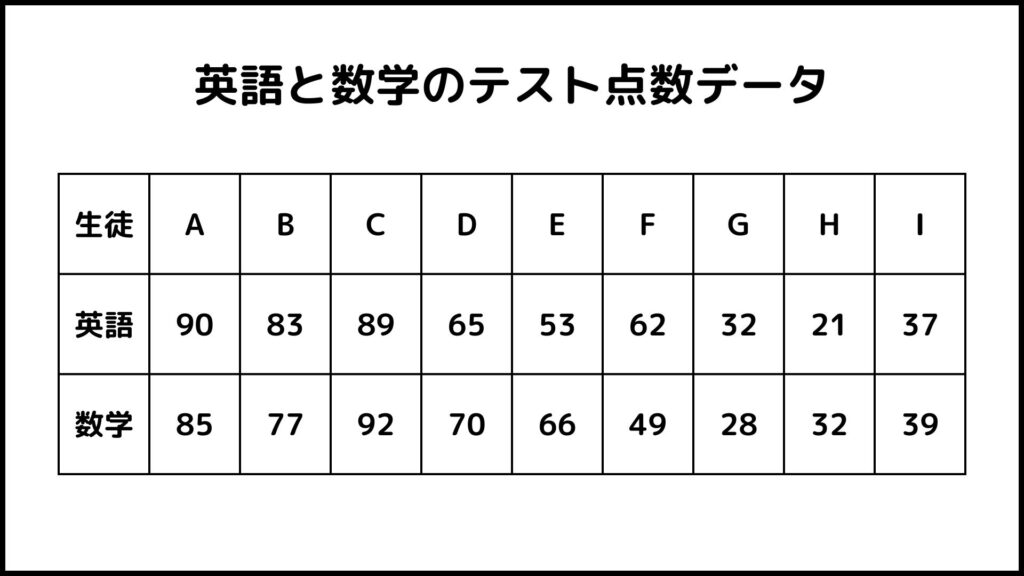
このデータはある学校における生徒9人の英語と数学のテスト点数のデータです。散布図にしてみてみましょう。
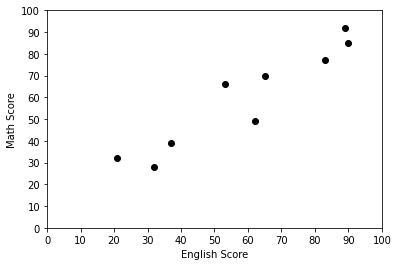
横軸が英語のテストで縦軸が数学のテストです。この散布図を見ると9つのデータを3つのグループに分けることができそうです。
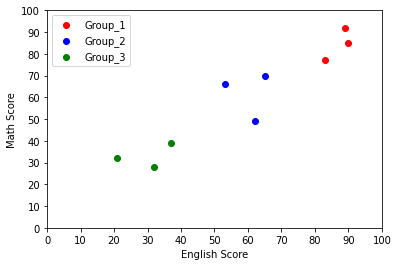
上のグラフのように赤、青、緑の3つのグループに分類できそうですね。このように似たようなデータを同じグループに分類することをクラスタリングと言います。
エルボー法ってなに?
エルボー法はクラスタリングにおいて最適なグループ数を見つけるための方法です。sseと呼ばれる評価指標を使うので、まずはsseの説明からしたいと思います。
sse(クラスタ内誤差平方和)ってなに?
sseは各グループの中心点とそのグループに属すデータ点の距離の二乗を合計したものです。

クラスタリングでよく使われるk平均法はこのsseを最小化することによってグループ分けを行っています。
sseはグループ数が増えると減少します。それはグループが細分化されて、より近いデータ点しか1つのグループに属さなくなるからです。
エルボー法はグループの数が増えていったときにsseがどれだけ減少するかを見て最適なグループ数を判断する方法です。
それでは次にエルボー法について解説したいと思います。
エルボー法ってなに?
エルボー法はグループ数が増えていったときにsseがどれだけ減少するかを見て最適なグループ数を判断する方法です。
下のグラフを見てみましょう。

このグラフは横軸がグループの数、縦軸がsseを表しています。これを見るとやはりグループ数が増えるとsseが減少することが分かりますね。
しかし減少具合はどうでしょうか。
グループ数が1から2に増えるとものすごくsseが減少しています。一方でグループ数が9から10に増えてもほとんどsseは減少していません。
先ほど言ったようにk平均法はこのsseを最小化することによって最適なグループ分けを行っています。
つまりグループ数が1から2に増えることはクラスタリングの最適化にめちゃめちゃ貢献しているけど、グループ数が9から10に増えてもクラスタリングの最適化にはほとんど貢献していないということです。

このことを踏まえてもう一度グラフを見てみましょう。
グループ数が3まではsseが割と減少していますが、グループ数が3から4になってからはあまりsseが減少していないことが分かります。
つまりグループ数を3に増やすところまではクラスタリングの最適化に貢献しているがグループ数を4以上に増やしてもあまり最適化には貢献できていないというわけです。
以上のことから最適なクラスタ数は3ということが分かります。
このようにグループ数の増加によるsseの減少具合を見て最適なグループ数を見つける方法をエルボー法と言います。
エルボー法をpythonでやってみる
今回使うデータはscikit-learnが提供しているIris plants datasetを使いたいと思います。
Iris plants datasetは3種類のIrisという花に関するデータセットです。このデータセットにはsepal length(萼の長さ)、sepal width(萼の幅)、petal length(花弁の長さ)、petal width(花弁の幅)そしてそれぞれの花の種類データが入っています。
3種類のIrisはIris-setosa, Iris-Versicolour, Iris-Virginicaという名前で、それぞれ0, 1, 2と番号付けされています。
この記事は「クラスタリングとk平均法」の続きなので、この記事で解説したことは知っている前提で解説したいと思います。
ということでグラフを作成しましょう。
SSE = [] # sseを入れる用の空リストを作成
for i in range(1, 11): # グループ数を1から10までfor文でまわす
kmeans = KMeans(n_clusters=i, random_state=0) # k平均法 のモデルを定義.
kmeans.fit(data) # k平均法の実行
SSE.append(kmeans.inertia_) # SSEにsseを加える
plt.plot(range(1, 11), SSE) # 横軸グループ数、縦軸sseの折れ線グラフを作成
plt.xlabel('n_clusters') # x軸のラベルをn_clustersに設定
plt.ylabel('sse') # y軸のラベルをsseに設定
plt.xticks(range(1,11,1)) # x軸の目盛りを設定
plt.show() # グラフを表示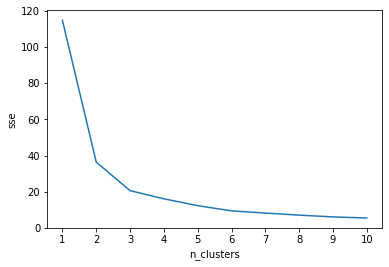
1つずつコードを解説していきます。
1行目はsseを保管しておくための空リストを作っています。
3行目から6行目ではグループ数が1から10のときにクラスタリングを実行し、sseを計算してSSEに加えています。sseは.inertia_で求めることができます。また.append()リストに追加することができます。
ここまででグラフを作るためのデータの準備ができたので、9行目から15行目でグラフを作成しています。
以上でグラフの作成ができたので、エルボー法の説明でやった手順で最適なグループ数を求めてみましょう。
クラスタ数が3まではsseが結構減少していますが、4以降はあまりsseが減少していませんね。
ということで最適なグループ数は3だということが分かりました。
今回使ったデータセットは3種類のIrisという花に関するデータセットなので、ちゃんと正しい分析ができていますね。
おわりに
いかがでしたでしょうか。
今回の記事ではpythonを使ってクラスタリングについて説明していきました。こんな感じでプログラミングを使えばいろいろなことができます。非常に興味深いですよね。
データの数値をいじるとまた違う結果が得られるので興味がある人はぜひやってみてください!またこの記事ではクラスタリングの中でも非階層的クラスタリングについて説明しました。他にも色々な手法があるので是非調べてやってみてください!
これからもこのようにプログラミングで色々やっていきたいと思います。ぼくが一番勉強になるので続けていきたいです!
最後までこの記事を読んでくれてありがとうございました。
この記事が役に立ったら幸いです。
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。





