こんにちは!しゅんです!
この記事ではマイケルジョーダンのすごさを数字を使って解説しています。
この記事では1987年~1988年のレギュラーシーズンのデータを使って分析します。
普段はNBAのデータ分析に関する記事を書いたりしています。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
それではやっていきましょう!
マイケルジョーダンのオフェンス面のすごさ
マイケルジョーダンのディフェンス面のすごさ
データを手に入れる
今回分析に使うデータはNBA REFERENCEの1987-1988シーズンのレギュラーシーズンのデータです。
データはこちらのサイトから入手しました!
それではこのデータを使って分析していきましょう!
分析をするには事前準備が必要不可欠ですが、これらは本題とはあまり関係がないので飛ばします。
データの前処理はこちらの記事でも解説しています!
また今回はpandas, numpy, matplotlib, seabornを使って分析したいと思います。これらはデータ分析をするときにとてもよく使う便利なライブラリです。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns分析に用いるデータはあ87-88_pという名前でgoogle driveに置いてあるので、マウントしてgoogle colabに読み込みます。
# データを読み込む
df = pd.read_csv("data/87-88_p.csv")また分析には82試合中42試合以上出場した選手のみを対象にします。
# 42試合以上出場した選手データのみを抽出する
df_42 = df[df["G"] >= 42]中身を見てみましょう。
# データの中身を表示
df_42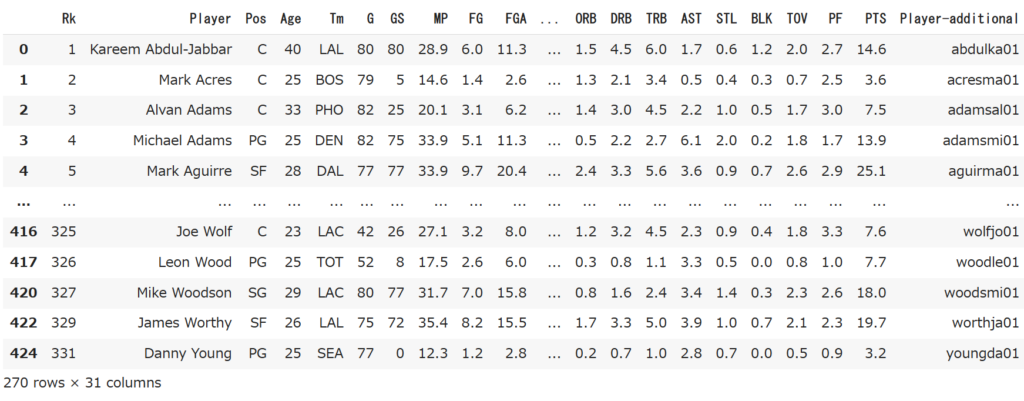
選手の名前、ポジションなどのデータから得点数、スティール数などの計31項目のデータがそろっています。また左下を見たらわかるように、270選手分のデータが格納されています。
またPosの中身を見てみると複数のポジションになっている人がいるのでそこを修正しましょう。
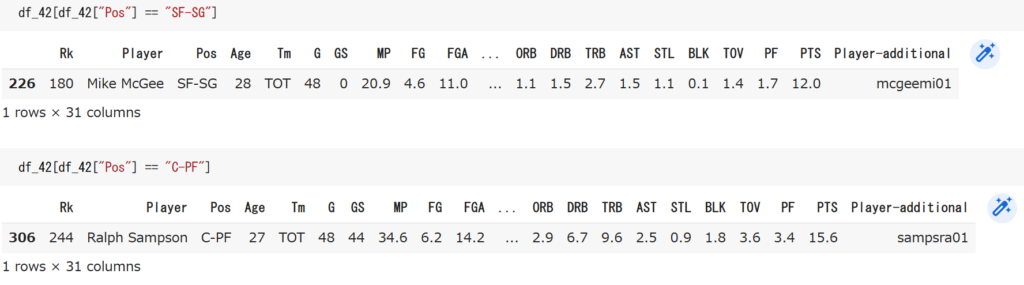
この2選手が複数ポジションになっているので、今回は彼らがキャリア全体でより多くプレイしたポジションに合わせました。
# 226番の選手「Mike McGee」のPosをSFに変更
df_42.at[226,"Pos"] = "SF"
# 306番目の選手「Ralph Sampson」のPosをPFに変更
df_42.at[306,"Pos"] = "PF"散布図を描いてみる
まずはジョーダンがいかに優れていたかを見るために散布図を書いてみましょう。
このシーズンでジョーダンは平均35得点を残して得点王、平均3.2スティールを残してスティール王またガードなのに平均1.6ブロックを残し、その他もろもろ含めてMVPと最優秀守備選手賞を受賞しました。
ここでは平均得点数と平均ブロック数を評価軸にして、オフェンスとディフェンスでジョーダンがいかに優れていたかを散布図を使って確かめてみたいと思います。
まずはジョーダンがガードの中でどれほど飛びぬけていたかを見ていきます。
# df_42の中からPos(ポジション)がPGとSGの選手のみ抽出してdf_Gと名付ける
df_G = df_42[df_42["Pos"].isin(["PG", "SG"])]散布図はmatplotlibとseabornを使って描いていきます。これらはpythonでグラフを作るのに非常に便利なライブラリです。
# グラフを見やすくするための事前準備
plt.rcParams['font.family'] = 'Liberation Sans' # グラフの文字フォントを設定
plt.rcParams['font.size'] = 14 # 文字サイズを設定
plt.rcParams['font.weight'] = 'bold' # 文字の太さを設定
plt.figure(figsize=(10,6)) # グラフの大きさを設定
# 散布図を作成(x軸が平均得点数, y軸が平均ブロック数, 色はsalmonとmediumaquamarine, 透過度は0.7, データ点のサイズは500)
sns.scatterplot(data=df_G,
x="PTS", y="BLK", hue="Pos" ,palette=['salmon', 'mediumaquamarine'], alpha = 0.7, s = 500)
plt.xticks(np.arange(0, 41, 5)) # x軸の目盛りを0~40を5刻みにする
plt.yticks(np.arange(0, 2.2, 0.2)) # y軸の目盛りを0~2.2を0.2刻みにする
# グラフを表示
plt.show()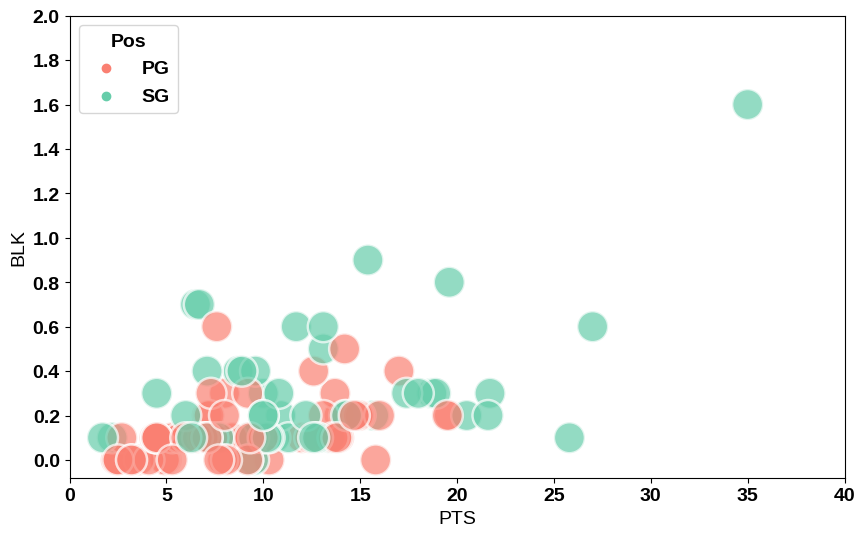
ということでできました。
なぜか右上に1つだけ仲間はずれな点がある…
そうです。これがマイケルジョーダンです。この図を見ると当時の他のガードの選手と比べてジョーダンがいかに人間離れなスタッツを記録していたかが分かると思います。
そしてこの記録はガードだけではなく、ビッグマンを含めてもおかしな数値なんです。
それでは次にビッグマンの中にマイケルジョーダンのスタッツを混ぜて散布図を作ってみましょう。
先ほど同様に、今度はPosがPFとCの選手のみを抽出します。
# df_42の中からPosがPf, Cの選手のみを抽出してdf_bigと名付ける
df_big = df_42[df_42["Pos"].isin(["PF", "C"])]そしてそこにジョーダンのデータをくっつけます。
# df_bigとジョーダンのデータをくっつける。
df_big_MJ = pd.concat([df_big, df_42[df_42["Player"] == "Michael Jordan"]], axis = 0)マイケルジョーダンのポジションをSGからMJに変更してみましょう。
# ジョーダンのポジションをMJにする(ジョーダンのデータは188番目にある)
df_big_MJ.at[188,"Pos"] = "MJ"それではこのデータを使って先ほどと同じように散布図を書いてみましょう。
# 図のサイズを設定し、軸を透過させる
plt.figure(figsize=(10,6), facecolor='None')
# 散布図を作成(さっきとほぼ同じ、色を赤青緑に指定)
sns.scatterplot(data=df_big_MJ,
x="PTS", y="BLK", hue="Pos" ,palette=['red', 'blue', "green"], alpha = 0.7, s = 500)
# df_big_MJのブロック数の平均値をmean_xと名付ける
mean_x = df_big_MJ["BLK"].mean()
# 散布図上にブロック数の平均値を横線で表す(色は黒、点線、太さ3、AVERAGEというラベルをつける)
plt.axhline(mean_x, color='black', ls = ":", lw = 3, label = "AVERAGE")
# ラベルを表示
plt.legend()
# 図を表示
plt.show()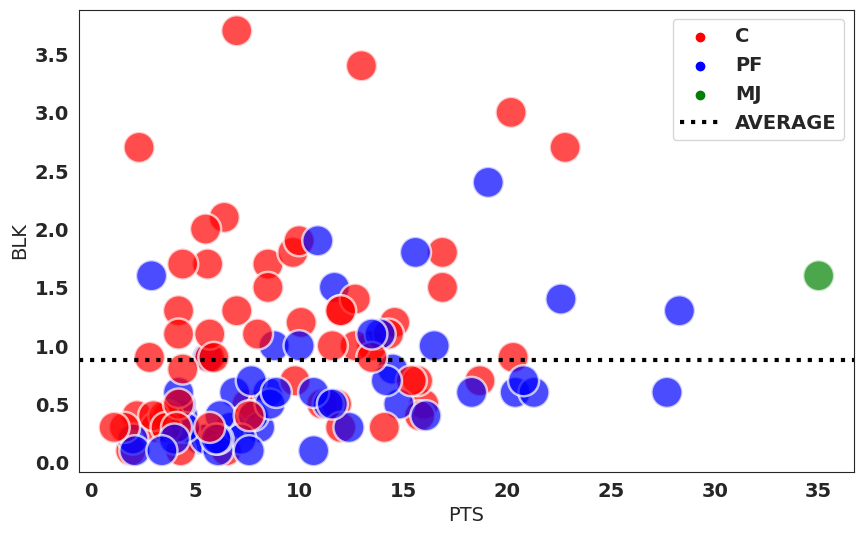
ジョーダンは右の緑色の点です。そして点線がdf_big_MJのブロック数の平均値です。
# df_big_MJのブロック数の平均値を表示
df_big_MJ["BLK"].mean()
df_big_MJのブロック数の平均値が約0.9ということで、ジョーダンはこの数値を大きく上回っています。これを見るとガードでこのブロック数を記録していることがどれだけすごいことなのかが分かりますね。
偏差値を求めてみる
続いてはジョーダンのスタッツを偏差値を使って表していきたいと思います。偏差値を求めるためにはまず標準化をして標準得点を求める必要があるのでやってみましょう。
まずはdf_42を標準化するデータとしないデータに分けましょう。
# 標準化しないデータを抽出
df_stn = df_42[["Rk", "Player", "Pos", "Age", "Tm", "G", "GS", "MP"]]
#標準化するデータを抽出
df_st = df_42.drop(["Rk", "Player", "Pos", "Age", "Tm", "G", "GS", "MP", "Player-additional"], axis=1)選手名、ポジションなど数値化できないものや、今回の分析には使わない年齢といったデータは標準化せず、それ以外のデータを標準化したいと思います。
標準化はscikit-learnのStandardScalerを使うとできます。scikit-learnはpythonでデータ分析や機械学習をするのに非常に便利な学習ライブラリです。
# scikit-learnからStandardScalerをインポート
from sklearn.preprocessing import StandardScaler
# 標準化を実施(df_stwを標準化してdf_scaledという名前にする)
scaler = StandardScaler()
df_scaled = scaler.fit_transform(df_st)ということで標準化ができ、df_scaledには各選手の標準得点のデータが格納されています。偏差値を求めるにはこれらを10倍して50を足す必要があります。
# 偏差値を求める
df_T = df_scaled*10 + 50最後に先ほど切り離した標準化しないデータとくっつけましょう。
df_stn = df_stn.reset_index()
df_hensati = pd.concat([df_stn, df_T], axis = 1)df_hensatiの中身を見てみましょう。
df_hensati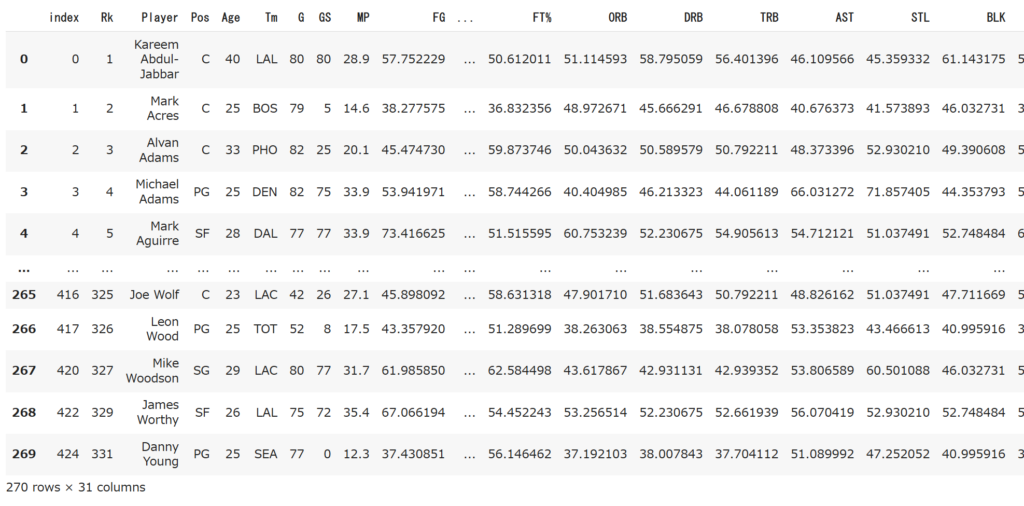
それではジョーダンの偏差値を見てみましょう。全部見るのはめんどくさいので今回はPTS, FG%, BLK, STLの4項目を調べます。
# df_hensatiからPlayerがMichael Jordanのデータだけを抽出
Jordan = df_hensati[df_hensati["Player"] == "Michael Jordan"]
# JordanのPTS, FG%, BLK, STLを表示
Jordan[["PTS","FG%","BLK","STL"]]
ということでジョーダンのスタッツを偏差値で表すことができました。どれも50を超えていますが、やはり得点数とスティール数の数値がバグってますね…
同じようにしてガードだけを対象にした場合のジョーダンの偏差値も求めることができるので、ぜひやってみてください!
クロス集計表をつくる
最後に当時のガードがどれだけ得点するのが難しかったかをクロス集計表を用いて分析してみたいと思います。
2×2のクロス集計表を作るために、評価軸は「ガードかガード以外か」、そして「リーグの平均得点以上か以下か」にしたいと思います。
# PTSの平均値を計算する
mean_pts = df_42['PTS'].mean()
# カテゴリーを定義する
pos_cat = pd.cut(pd.to_numeric(df_42['Pos'].replace({'PG': 1, 'SG': 1, 'SF': 0,'PF': 0,'C': 0})), bins=[-float('inf'), 0, float('inf')], labels=['Non-G', 'G'])
pts_cat = pd.cut(df_42['PTS'], bins=[-float('inf'), mean_pts, float('inf')], labels=['Below Mean', 'Above Mean'])
# クロス集計表を作成する
ct = pd.crosstab(pos_cat, pts_cat)
# 結果を表示する
print(ct)
オッズ比を計算してみると約1.2でした。この数字は「ガードの選手がリーグの平均得点以下になること」は「ガード以外の選手がリーグの平均得点以下になること」に比べて約1.2倍起こりやすいということを表しています。
概要欄にも書きましたが、動画の方ではGにSGを含めずに計算してしまいました。ただしくはこちらの結果になります。申し訳ございません🙇
比較するために2021-2022でも同じように集計してみると以下のようになりました。

オッズ比を計算してみると約0.5でした。この数字は「ガードの選手がリーグの平均得点以下になること」は「ガード以外の選手がリーグの平均得点以下になること」に比べて約0.5倍起こりやすいということを表しています。
つまりガードの方が約2倍リーグ平均以上の得点しているということを表しています。
これらの数字を見ると、1980年代のNBAにおいてガードの選手がどれだけ得点していなかったかが分かると思います。その中でジョーダンはあれほどの数字を記録しており、そのすごさが分かりますね。
おわりに
いかがでしたでしょうか。
今回の記事ではマイケルジョーダンのすごさについて説明していきました。こんな感じでプログラミングを使えばいろいろなことができます。非常に興味深いですよね。
今回の記事はYouTubeでも解説しています!そちらもぜひ見てみてください!
これからもこのようにプログラミングで色々やっていきたいと思います。ぼくが一番勉強になるので続けていきたいです!
最後までこの記事を読んでくれてありがとうございました。
この記事が役に立ったら幸いです。




