こんにちは!しゅんです!
今回はカウントソートについて解説していきます!
データを分析するときに小さい順に数字を並べる操作は頻繁に行います。そんなときに使うのがカウントソートという手法です。
この記事ではカウントソートというアルゴリズムについて、基本的な考え方や実装方法を分かりやすく解説していきます。
また今回はpythonを使って実際にカウントソートを実装していきたいと思います。
それでは解説していきましょう!
他のソートの手法についてはこちらの記事で解説しています!
普段はNBAのデータ分析をしたりしています。
ぜひこちらの記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
カウントソートの基本的な考え方
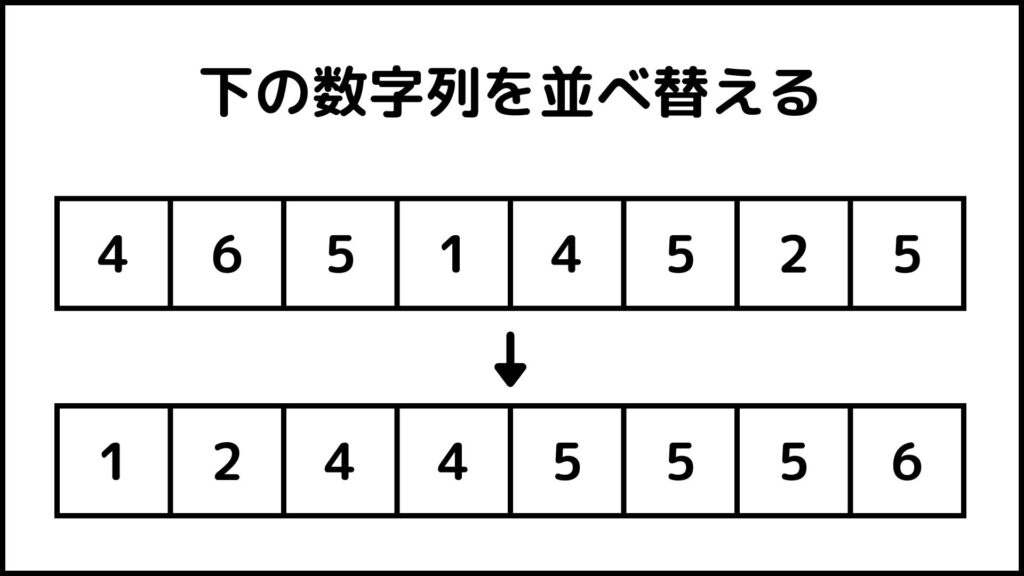
カウントソートは名前の通り数字が登場する回数を数えてソートします。下の例を使ってカウントソートの基本的な考え方を説明していきます。
要素の個数を数える
上の数字列を下の数字列のように小さい順にソートすることを考えます。カウントソートでは数字列に含まれている要素の数を数えます。
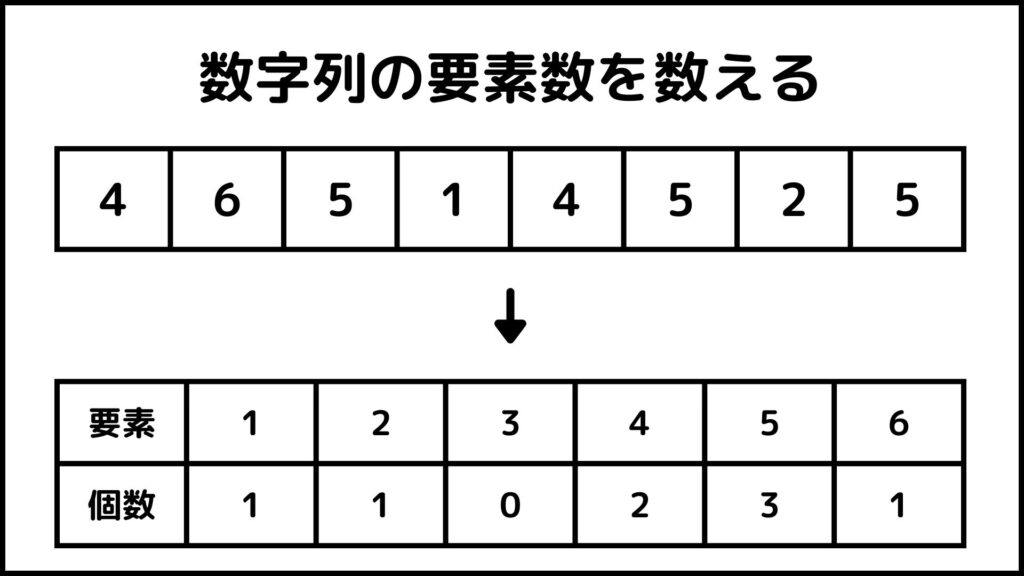
数字列を見ると1が1個、2が1個、3が0個、4が2個、5が3個、6が1個あります。そしてこれを使って今度は個数の累積を計算します。
個数を累積で計算する
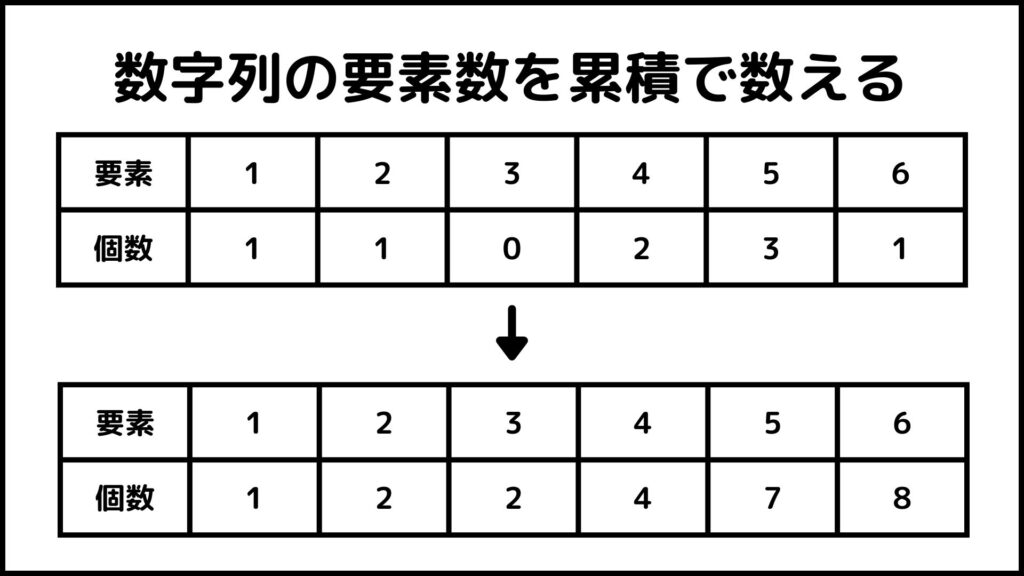
累積なので自分の数字までの個数を足し算して計算します。例えば要素数が4の累積個数を計算するには、要素が1、2、3、4の個数を全部足します。つまり1+1+0+2=4となります。
ここまでで事前準備が完了したので、この累積個数のリストを使って並べ替えをしていきます。
累積個数を使って並べ替える
結論手順は以下の通りになります。具体例を使って説明するのでまずは手順を見てみましょう。なお並べ替えたい数字列を\(A\)、\(A\)の長さ(上の例で言うと8)を\(n\)、累積個数のリストを\(C\)とします。
- \(j =nとする\)
- \(空の数字列Bを用意し、C[A[j]]番目をA[j]とする\)
- \(C[A[j]]を1少なくする\)
- \(jを1少なくする\)
\(j \geq 1ならSTEP. 2に戻る\)
\(j = 0になったらBを返す\)
文字が多くて理解するのが難しいと思うので先ほどの例を使って説明します。\(A=[4, 6, 5, 1, 4, 5, 2, 5], \; C = [1,2,4,7,7,8]\)とします。それでは1つずつ解説していきましょう。
まず\(j=n=8\)とします。\(A[j]=A[8]=5\)なので\(C[A[j]] = 7\)となります。したがって空のリスト\(B\)の7番目を5として\(C[5] = 6, \; j = 7\)とします。
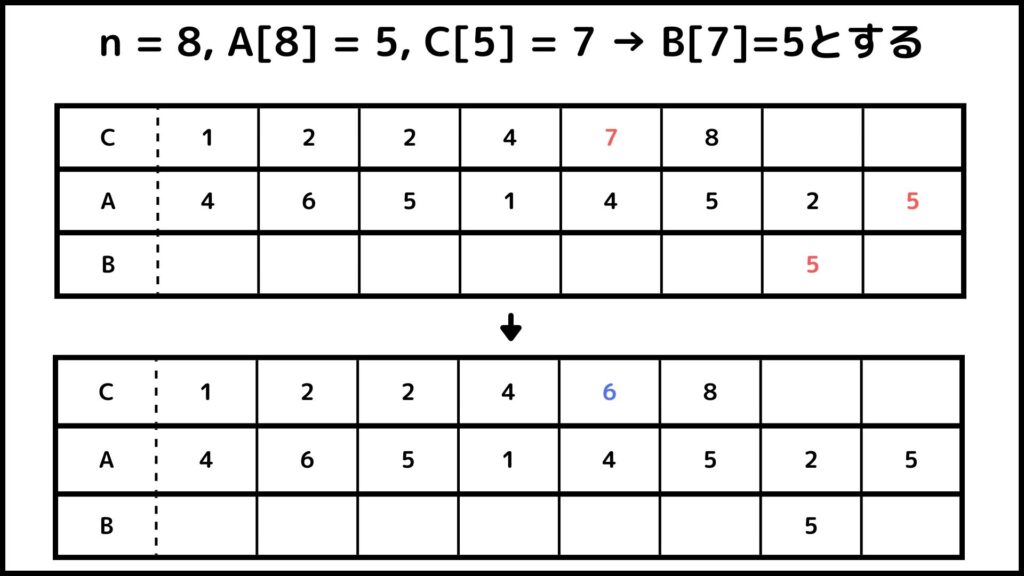
これ以降も同じように計算していきます。ここからは図を使って流れを説明していきます。
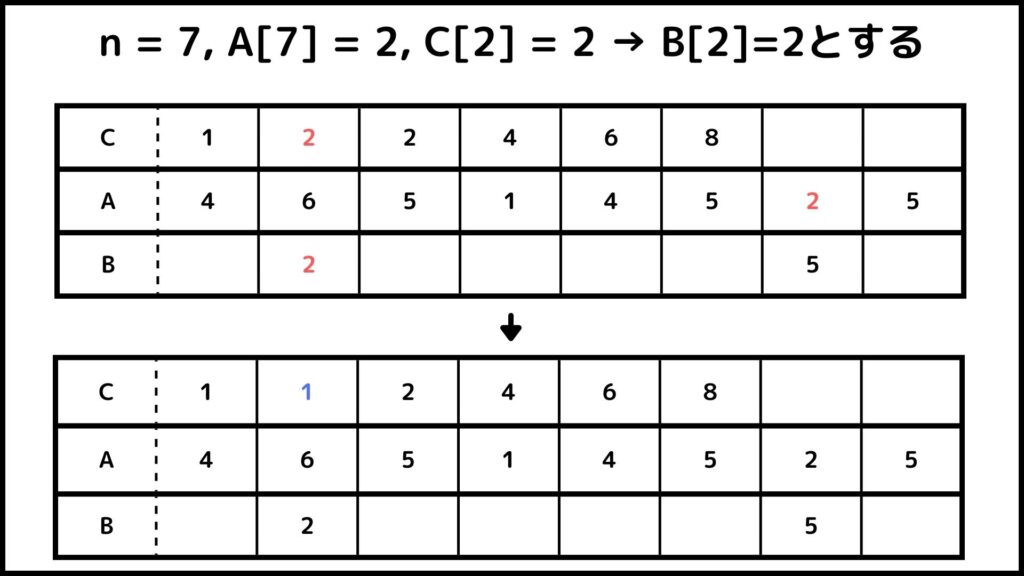
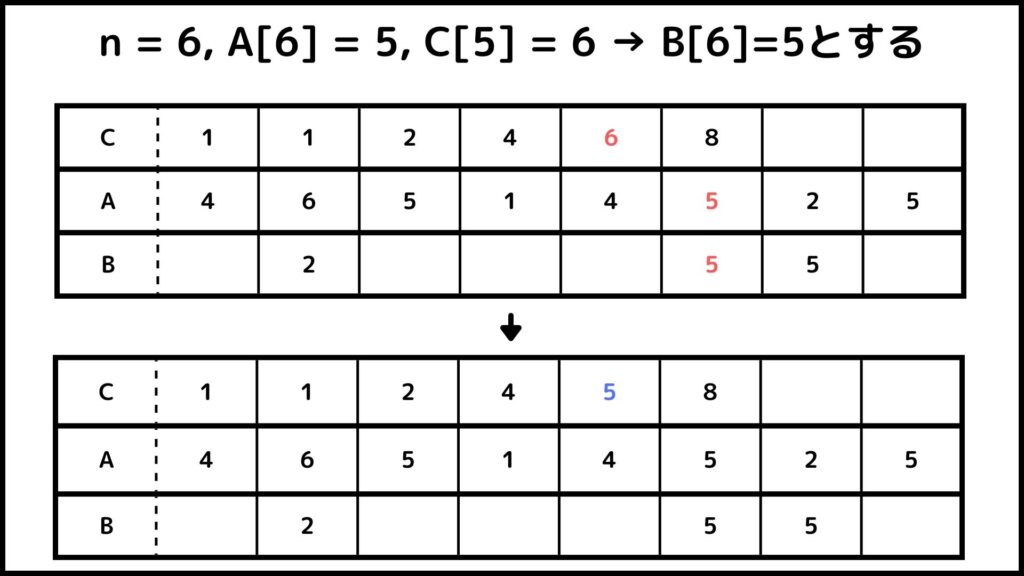
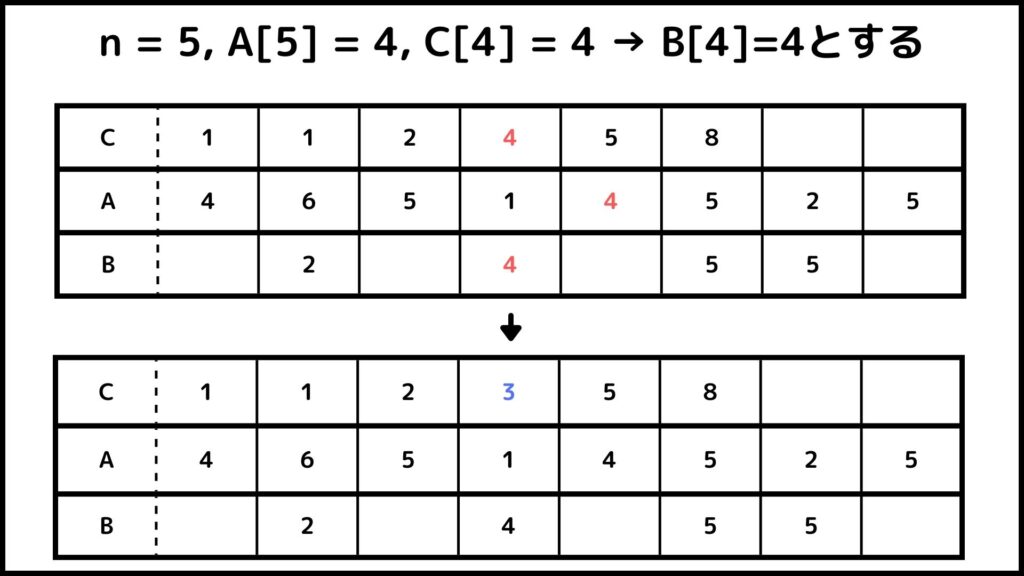
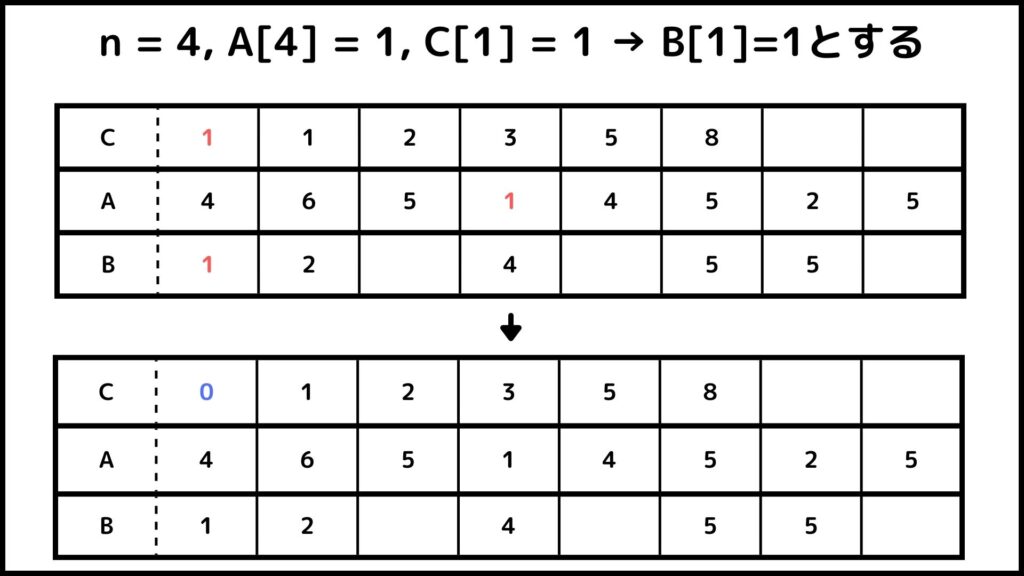
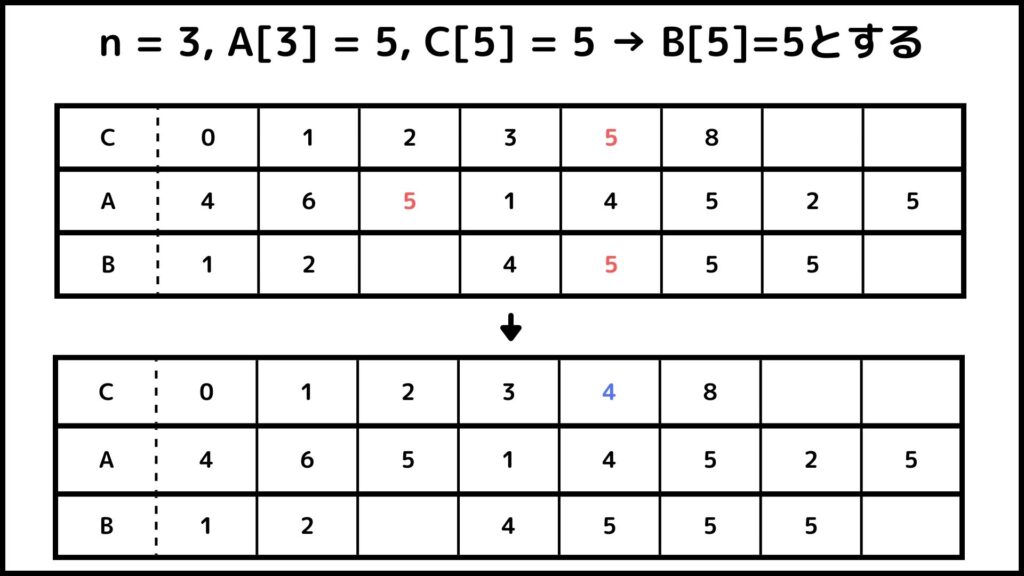
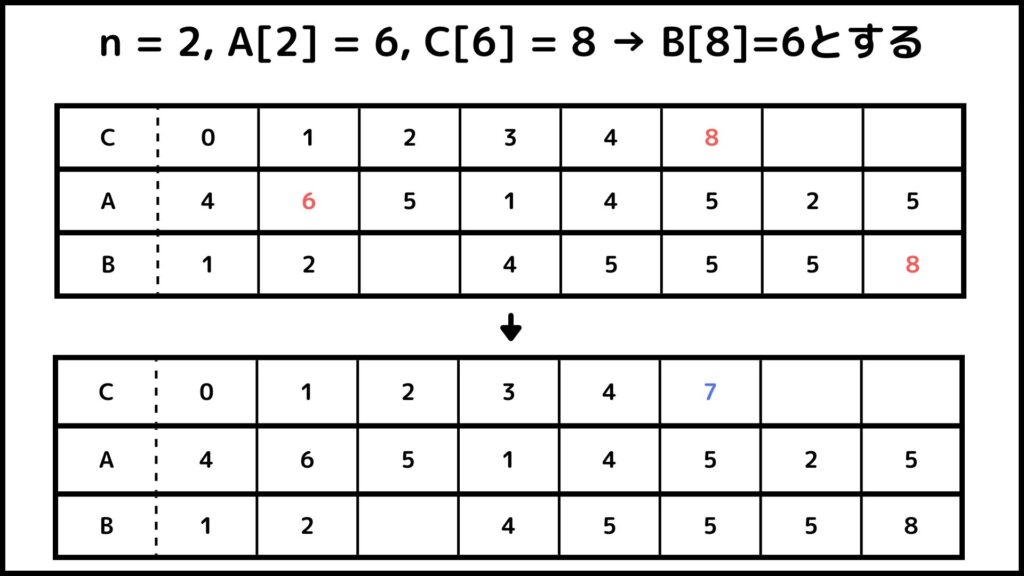
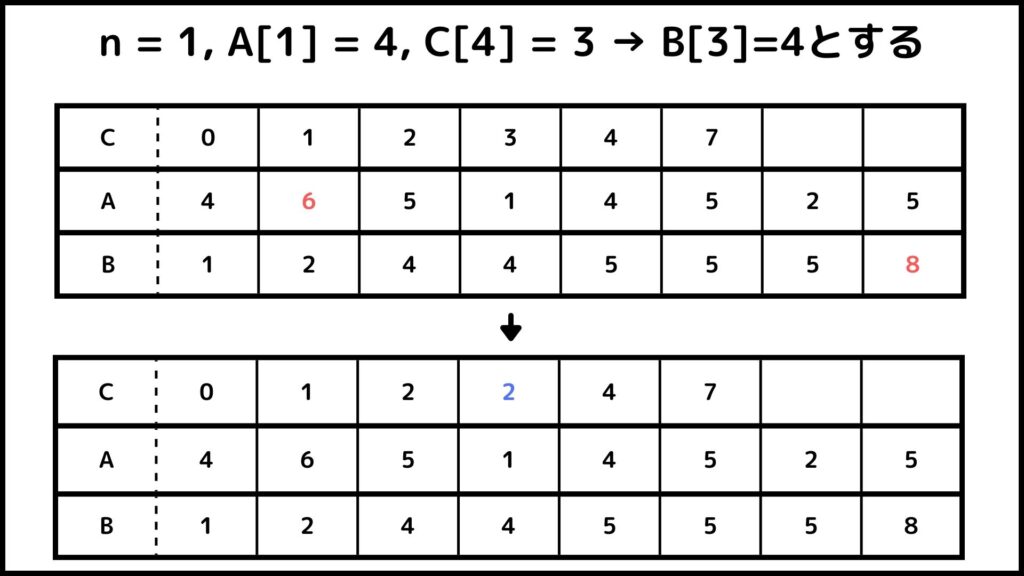
ということでカウントソートでができました。Bを見てみるとちゃんと小さい順に並べ替えされているのが分かりますね。
カウントソートをpythonで実装してみる
プログラムは以下のようになります。
def counting_sort(A):
# 累積個数を計算する
k = max(A) + 1 # k をAの最大値+1とする
C = [0] * k
# 登場した要素の個数を数える
for j in range(len(A)):
C[A[j]] += 1
# 5~7行目で作ったCを使って累積個数を計算する
for i in range(1, k):
C[i] += C[i-1]
B = [0] * len(A) # 空リストBを作る
# 累積個数を使ってソートする
for j in range(len(A)-1, -1, -1):
B[C[A[j]]-1] = A[j]
C[A[j]] -= 1
return B2行目から10行目で各要素の累積個数を計算しています。5行目から7行目ではとりあえずAに各要素が何個あるかを数えてCに格納しています。8行目から10行目ではそれまでに作成したCを使って累積個数を計算しています。10行目までで累積個数を計算したリストCが完成しています。
12行目では答えを格納するための空リストBを作っています。14行目から18行目では、完成したCを使って並べ替えた数字をBに格納しています。
以上の過程で数字をソートしています。最後に実際にソートできているか確認してみましょう。
# ランダムで1から100の数字を50個用意する
import random
Random_Numbers = []
for i in range(50):
Random_Numbers.append(random.randint(1, 100))
#カウントソート関数を使ってソートする
Sorted_Numbers = counting_sort(Random_Numbers)
#ソートする前とソートした後をグラフで表示する
import matplotlib.pyplot as plt
plt.figure(figsize = (10,4))
ax1 = plt.subplot(121)
ax1.bar(range(len(Random_Numbers)), Random_Numbers)
# x軸・y軸のラベルの設定
ax1.set_xlabel('Index')
ax1.set_ylabel('Value')
# グラフのタイトルの設定
ax1.set_title('Random Numbers')
ax2 = plt.subplot(122)
ax2.bar(range(len(Sorted_Numbers)), Sorted_Numbers)
# x軸・y軸のラベルの設定
ax2.set_xlabel('Index')
ax2.set_ylabel('Value')
# グラフのタイトルの設定
ax2.set_title('Sorted Numbers')
# グラフの表示
plt.show()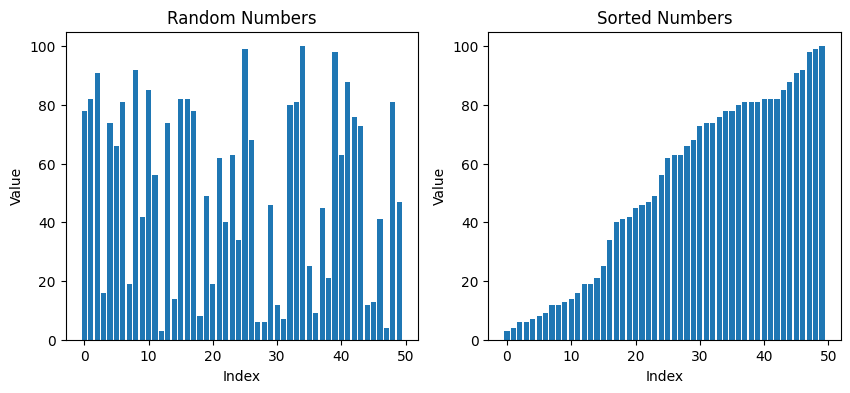
上のコードは1から100の数字をランダムに50個生成し、そのまま並べたときとカウントソートで並べ替えたときの2パターンをグラフで表したものです。これを見るとちゃんと小さい順に並べ替えることができていますね。
カウントソートの特徴
特徴1. 計算量が少ない
カウントソートは普通のソートに比べて計算量が少ないです。
数字を小さい順に並べるソートにはバブルソート、選択ソート、クイックソート、挿入ソートなどたくさんの種類がありますが、どれを使えば良いかの指標に計算量というものがあります。
計算量とはあるアルゴリズムを使ったときにだいたいどれくらい時間がかかるかを評価したもので、これが小さければ小さい程良いアルゴリズムだと言われます。
ここからは少し難しい話になります。普通のソートの計算量は\(O(n^2)\)ですが、カウントソートの計算量は\(O(n+k)\)となります。(\(n\)は要素数で\(k\)は要素の最大値)計算量の表記を説明するとそれだけで1つの記事が書けそうなので今回は省略します。結論カウントソートの方が早く計算できると思ってください。
特徴2. アルゴリズムが安定である
カウントソートの2つ目の特徴としてアルゴリズムが安定であることが挙げられます。アルゴリズムが安定であるとは、数値が同じデータがあった場合に元の並び順と同じになるようにソートできるということです。
下の例を見てください。
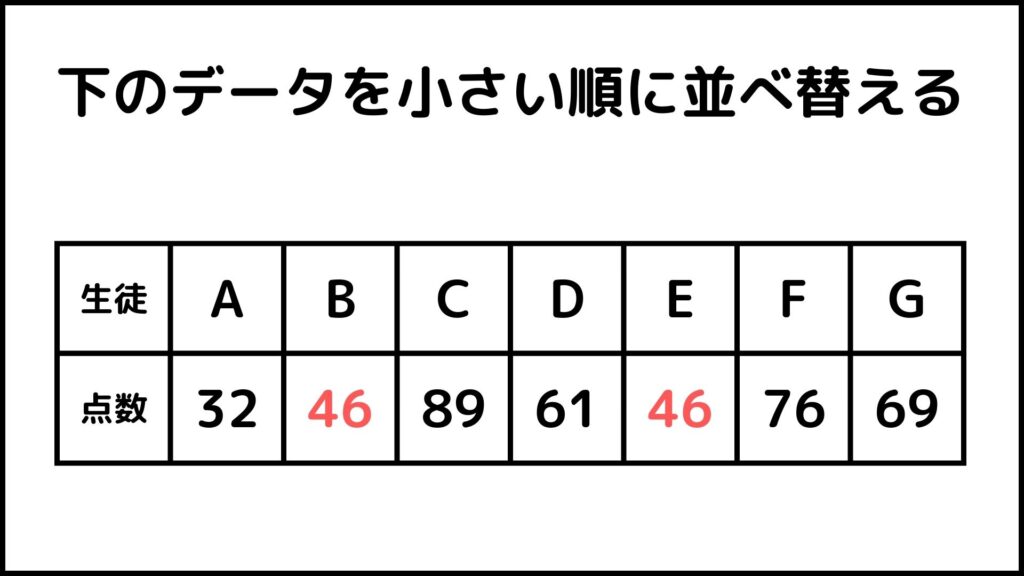
生徒の点数を小さい順に並べることを考えます。上のデータを見ると46点の生徒がB→Eの順番で二人いますね。安定なソートアルゴリズムを使用した後の数字列は必ずB→Eの順番になります。
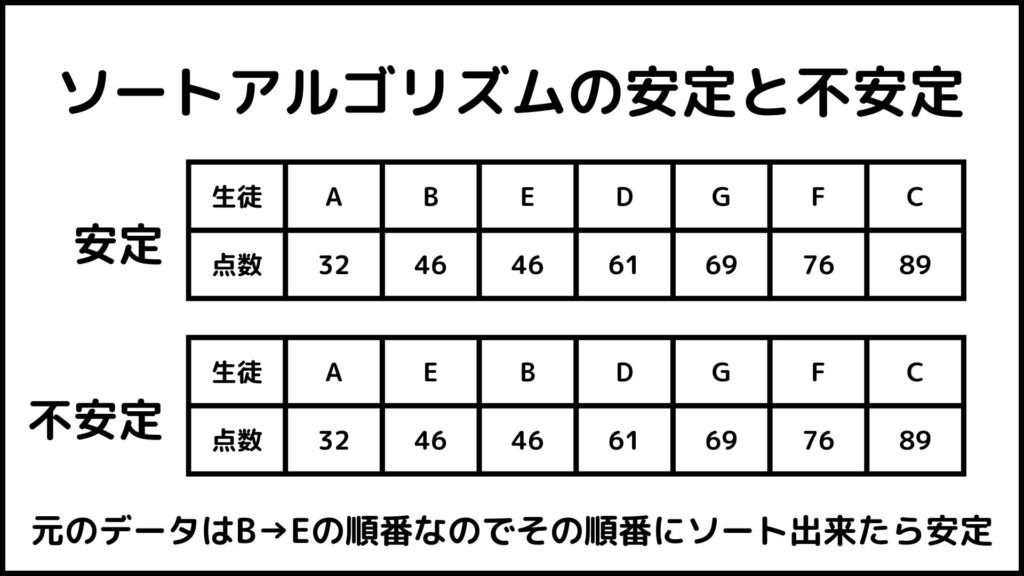
おわりに
いかがでしたか。
今回の記事ではカウントソートについて解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。





