こんにちは!しゅんです!
いきなりですが遠足に持っていくお菓子って迷っちゃいますよね。
持っていきたいお菓子はたくさんあるけど300円以内とかの制限があるので食べたいお菓子を全部持っていくことはできないですよね。
ということでこの記事ではこの問題をナップサック問題として扱って、一番満足がいくように遠足に持っていくお菓子を決めていきたいと思います。また今回はpythonを使って実際にこの問題を解いてみたいと思います。
それでは解説していきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
今回使う数学の手法
今回はナップサック問題という数学における問題を使って遠足に持っていくお菓子を決めていきたいと思います!
ナップサック問題はこちらの記事で説明しています!
上の記事では選択肢を5個に設定したので、わざわざpythonを使わなくても頭で計算できるくらいの難易度でした。ということで今回は選択肢を20個にして問題を解いていきたいと思います!
ナップサック問題に関する詳しい説明は上の記事で説明しているので、今回の記事ではナップサック問題自体の説明は少なめでいきたいと思います。
問題の設定
それでは今回の問題を整理してみましょう。
今回扱う問題
・遠足に持っていくお菓子を決める。
・20個のお菓子の中から持っていくものを選ぶ。
・合計300円までしかお菓子を持っていけない。
・同じお菓子は1つまでしか持っていけない。
・お菓子1つ1つに値段と満足度が割り当てられている。

問題を数式で表す
それでは上記の問題を数式で表してみましょう。変数の設定、目的関数の設定、制約条件の設定の順番で解説していきます。
変数の設定
今回の変数は「そのお菓子を買うなら1、買わないなら0」となるような変数にします。つまり0か1しかとらない0-1変数として設定します。
\(x_i \in \{0,1\} \;\;\;\;\;\;\;\;\;(i=1,2,…,20) \)
今回は最大で1個までしか持っていけないという制約ですが、例えば3個まで同じものを買っても良いという制約なら0-1変数ではなく「整数かつ0から3の範囲」という制約に変更します。
目的関数の設定
それでは今さっき設定した変数を使って目的関数を設定していきましょう。今回は満足度を最大化するようなお菓子の組合せを求めたいです。
例えばお菓子1の満足度が40のとき、お菓子1を持っていくと満足度が40増えます。
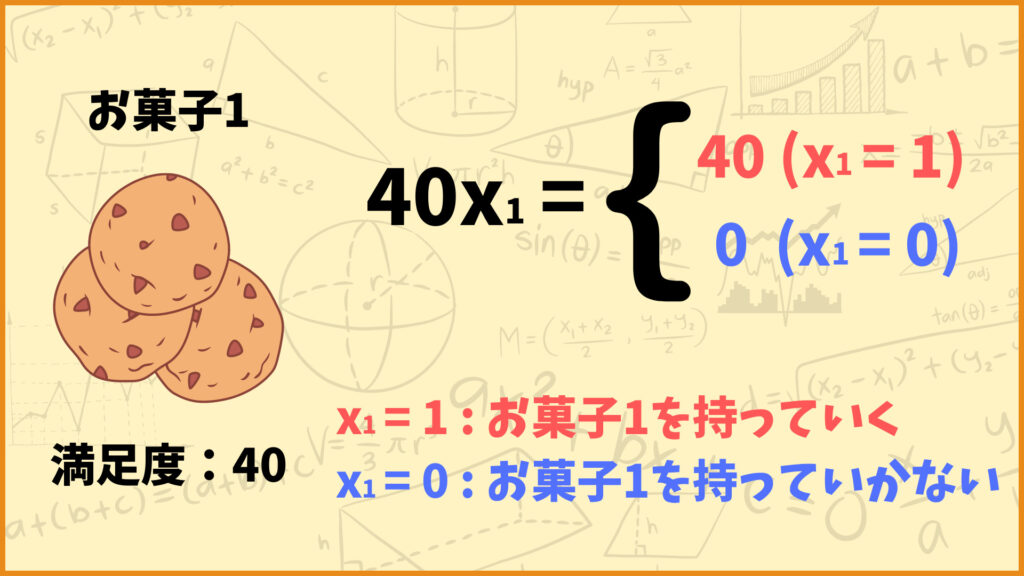
これを数式で表すと\(40x_1\)となります。この式は\(x_1=1\)のときは40、\(x_1=0\)のときは0になります。
これをすべてのお菓子に対して設定して足します。仮にお菓子1の満足度が40、お菓子2が30、お菓子3が15、…という風に続く場合、満足度を表す式は\(40x_1+20x_2+15x_3+…\)と表せます。
お菓子が5種類ぐらいしかなかったらこうやって表せるんですが、お菓子が20種類とかだとめっちゃ長くなっちゃいます。これを解決するためにベクトルを使って表したいと思います。

各お菓子の満足度を並べた列ベクトルを\(\boldsymbol{v}\)とします。\(\boldsymbol{v}\)には20個の満足度の数値が入っており、上の図で言うと左から順にお菓子1、お菓子2、お菓子3、…お菓子20の満足度の数値になっています。
また各変数を並べた列ベクトルを\(\boldsymbol{x}\)とします。\(\boldsymbol{x}\)には20個の変数が入っており、上の図で言うと左から順にお菓子1、お菓子2、お菓子3、…お菓子20の変数になっています。
どちらも列ベクトルで本当は各要素が縦に並ぶようなベクトルなんですが、図にするとすごいスペース取っちゃうので上図では転置させて横に並べてます。本当はどっちも縦に並んだベクトルであることに注意してください。
そして\(\boldsymbol{v}^{\top}\boldsymbol{x}\)を計算することで実は目的関数を設定することができるんです。(\(\top\)は転置の記号)
今回はこの目的関数を最大化したいので、以上のことをまとめると目的関数を以下のように設定することができます。
\(\max{\boldsymbol{v}^{\top}\boldsymbol{x}}\)
制約条件の設定
最後に制約条件の設定をしていきます。今回は持っていくお菓子の値段の合計が300円を超えないというのが制約条件です。

目的関数のときと同じようにこちらもベクトルを使って表してみます。各お菓子の値段を並べたベクトルを\(\boldsymbol{w}\)とします。\(\boldsymbol{w}\)には20個の数値が入っていて、左から順にお菓子1、お菓子2、お菓子3、…お菓子20の値段の数値になっています。
この\(\boldsymbol{w}\)と目的関数のところで使った\(\boldsymbol{x}\)をもう一回使って、制約条件に用いる関数を\(\boldsymbol{w}^{\top}\boldsymbol{x}\)と表すことができます。(ほぼ目的関数のときと同じです。)
どちらも列ベクトルで本当は縦に並ぶようなベクトルなんですが、図にするとすごいスペース取っちゃうので上図では転置させて横に並べてます。本当はどっちも縦に並んだベクトルであることに注意してください。
そして今回はこの関数が300を超えてほしくないので、以上のことをまとめると制約条件は以下のようになります。
\(\boldsymbol{w}^{\top}\boldsymbol{x} \leq 300\)
全部をまとめる
最後にここまで設定してきた数式を全てまとめて、今回の問題を数式で表してみましょう。
\(\text{max}\;\;\boldsymbol{v}^{\top}\boldsymbol{x}\)
\(\text{s.t.}\;\;\;\boldsymbol{w}^{\top}\boldsymbol{x} \leq 300\)
\(x_i \in \{0,1\} \;\;\;\;\;\;\;\;\;(i=1,2,…,20) \)
pythonで問題を解く
最後にpythonを使って問題を解いていきます。今回はpandasとnumpyとpulpを使います。pandasは表を作るのに便利なやつで、numpyは数値計算をするのに便利なやつで、pulpは数理計画法を扱うのに便利なやつです。
実行するコード
最終的には以下のコードを実行することで結果が得られます。
## ナップサック問題を解くための前準備
# pulpをインポート
! pip install pulp
from pulp import *
# pandasをインポート
import pandas as pd
# numpyをインポート
import numpy as np
# 満足度vをランダムに設定
np.random.seed(100)
v = np.random.randint(10, 100, 20)
# 値段wをランダムに設定
np.random.seed(200)
w = np.random.randint(10, 300, 20)
# 予算の上限を設定
capacity = 300
## ナップサック問題を設定して実際に解いてみる
# LpMaximizeで最大化に設定
prob = LpProblem(sense=LpMaximize)
# 変数の定義(まとめて定義)
x = [LpVariable(f"x{i}", cat = LpBinary) for i in range(1,21)]
# 問題の設定
prob += lpDot(v, x) # 目的関数を設定
prob += lpDot(w, x) <= capacity # 制約条件を設定
prob.solve() # 問題を解く
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示
for x in prob.variables():
print(x,"=", value(x)) # 最適解を表示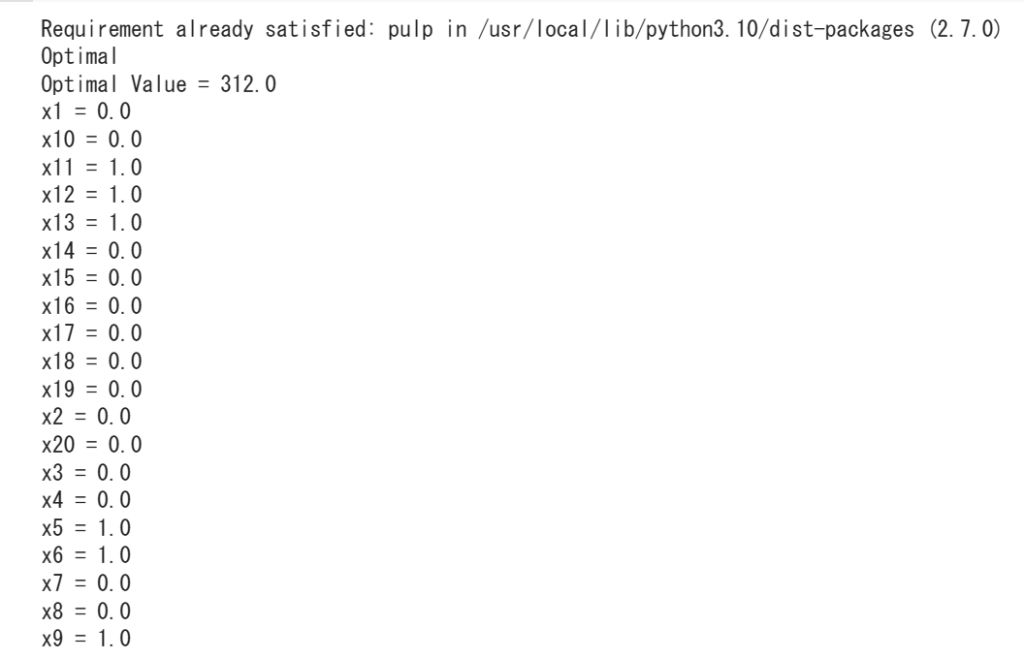
ナップサック問題のコードは前回の記事で説明しているのでこの記事では簡単にコードを説明したいと思います。
ナップサック問題のコードはこちらで詳しく解説しています!
コードの説明
事前準備
まず最初にpulp、pandas、numpyをインポートします。
# pulpをインポート
! pip install pulp
from pulp import *
# pandasをインポート
import pandas as pd
# numpyをインポート
import numpy as np満足度と値段と予算の設定
次に満足度と値段の設定をします。手動で設定するのは面倒くさいのでnumpyを使ってランダムな整数を20個生成しています。
# 満足度vをランダムに設定
np.random.seed(100)
v = np.random.randint(10, 100, 20)
# 値段wをランダムに設定
np.random.seed(200)
w = np.random.randint(10, 300, 20)
# 予算の上限を設定
capacity = 300np.random.seed()はランダムな数字を固定することができます。これ使わないと毎回違う満足度と値段になってしまうので出力結果が毎回同じになるようにします。かっこの中の数字は適当で大丈夫です。
np.random.randint()は指定した範囲の中で整数を生成します。満足度は10~100の間で20個数字を生成し、値段は10~300の間で数字を20個生成しています。
設定した満足度と値段のデータを見る
今回の問題には直接関係するわけではないですが、各お菓子の満足度と値段を表にして見てみましょう。ここでpandasのDataFrameを使います。
# 各お菓子の満足度と価格をデータフレームで表す
df = pd.DataFrame(data = [v,w],index = ["満足度","価格"],columns=[f"お菓子{i}" for i in range(1,21)])
# データフレームを転置させて表示
df.T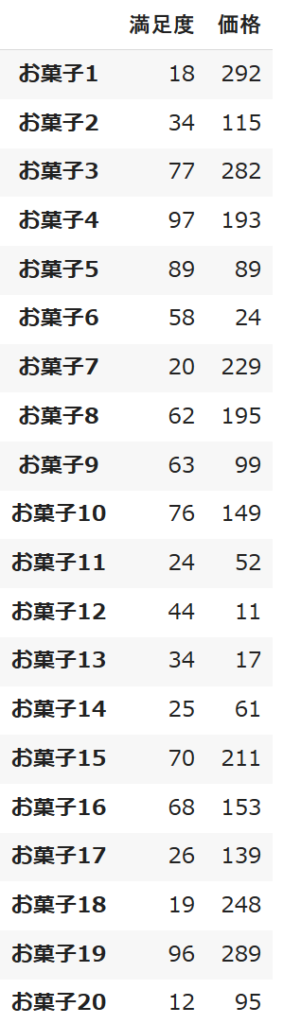
これを見るとお菓子4、お菓子19、お菓子5の順に満足度が高いですね。イメージ的にはこれらのお菓子が選ばれそうな気がします。
問題を解いて結果を表示する
最後に問題を解いて結果を表示しましょう。ここは前回と同じなので説明は省略します。
## ナップサック問題を設定して実際に解いてみる
# LpMaximizeで最大化に設定
prob = LpProblem(sense=LpMaximize)
# 変数の定義(まとめて定義)
x = [LpVariable(f"x{i}", cat = LpBinary) for i in range(1,21)]
# 問題の設定
prob += lpDot(v, x) # 目的関数を設定
prob += lpDot(w, x) <= capacity # 制約条件を設定
prob.solve() # 問題を解く
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示
for x in prob.variables():
print(x,"=", value(x)) # 最適解を表示結果を解釈する

これらのコードを出力すると上記の結果が出力されます。1行目はpulpがすでにインストールされていることを表しています。
2行目でOptimalって書いてあるのでちゃんと最適解が出力されていることが分かります。3行目で最適値を表示しています。今回の問題では312が最適値となっています。
4行目から下は最適解を出力しています。これを見るとお菓子5, 6, 9, 11, 12, 13が選ばれています。さっきの予想と結構違いますね。

満足度が高い上位2つのお菓子4とお菓子19が選ばれていませんね、なぜでしょうか。それはおそらく満足度は高いけどその分値段も高いからです。
満足度が100で値段が100のお菓子Aと満足度が50で値段が10のお菓子Bを比べてみると、満足度はお菓子Aの方が高いですが、満足度を値段で割った値はお菓子Bの方が大きいですね。
つまり1円当たりの満足度で言うとお菓子Bの方が大きいということで、言ってしまえばお菓子Bの方が効率よく満足感を味わえるということを表しています。
これを考慮するとなぜお菓子4とお菓子19が選ばれていないのが理解できますね。
より現実を反映させるために制約条件を色々変えてみるのも面白そうです。
制約条件を色々変えてみるのはこちらの記事で説明しています!
おわりに
いかがでしたか。
今回の記事ではナップサック問題について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。






