こんにちは!しゅんです!
この記事は前回の続きです。
ナップザック問題の制約条件を変えて結果がどうなるのかを試していきます!
前回のナップサック問題の記事はこちらから見れます!
前回の記事で「2個目以降は満足度が下がるように設定する」という所の説明を飛ばしたので、今回の記事ではそこの説明をしていきたいと思います。
それでは解説していきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
実装したいことを明確にする
元の問題
まず初めに実装したいことを明確にしておきます。前回の記事でテーマとした元のお菓子のナップザック問題は以下の通りです。
今回扱う問題
・遠足に持っていくお菓子を決める。
・20個のお菓子の中から持っていくものを選ぶ。
・合計300円までしかお菓子を持っていけない。
・同じお菓子は1つまでしか持っていけない。
・お菓子1つ1つに値段と満足度が割り当てられている。

変更したい制約条件
次に変更したい制約条件を明確にします。
変更したい制約条件
・同じお菓子を3個まで買っても良いことにする。
・1個目に比べて2個目以降は満足度が減少する。
どのように考えればよい?
それでは一体どのように考えればよいのかを1個ずつ解説していきます。まず最初にお菓子を1個買う場合と2個買う場合を考えてみます。
お菓子1を買ったときの満足度が100だとしましょう。

つまりこのお菓子を買ったとき満足度が100増えるということです。ではこのお菓子を2個買ったとき満足度は200増えるでしょうか。

現実的に考えて一杯目のラーメンの方が二杯目のラーメンよりおいしいと感じますよね。お菓子に関しても同じです。1個目の満足度が100だとしたら2個目の満足度は80とか70とかに減少してしまいます。
このように2個目以降の満足度が減少するのを経済学の用語で限界効用逓減の法則と言います!

2個目以降の満足度を減らす必要がある
ということで1個目の満足度が100だったら2個目は70とか80という風に減少させる必要があります。今回は割引率\(\delta\)を使って満足度を減少させていきます。
割引率\(\delta\)ってなに?
簡単に説明すると割引率\(\delta\)とは1個目と2個目でどれだけ満足度が小さくなるかを表すパラメータです。割引率\(\delta\)は\(0<\delta<1\)の間の値を取ります。

例えば\(\delta=0.8\)とします。1個目の満足度は別に割り引かれないので100になります。ところが2個目の満足度は1個目に比べて0.8だけ減少してしまうので満足度は\(100×0.8=80\)となります。
さらに3個目の満足度は2個目に比べて0.8だけ減少します。つまり1個目に比べて\(0.8^2=0.64\)だけ減少してしまうので満足度は\(100×0.8^2=64\)となります。
割引率\(\delta\)を使って満足度を減少させる
さっきのことを一般化しましょう。

一般に割引率が\(\delta\;(0<\delta<1)\)のとき満足度が100のお菓子1を3個買うことを考えます。
このとき1個目の満足度は\(100\)、2個目の満足度は\(100\delta\)、3個目の満足度は\(100\delta^2\)と表すことができます。
従ってこのときの満足度は\(100+100\delta+100\delta^2\)という風に表すことができます。
変数を設定する
1個目、2個目、3個目で変数を分ける
デフォルトの問題では変数を\(x_i\;(i=1,2,…,20)\)としています。この変数\(x_i\)は0-1変数で、お菓子\(i\)が選ばれたら1、選ばれなかったら0を取るような変数です。
例えば単純に3個まで買って良いことにするならこの変数の0-1制約を緩和して\(0 \leq x_i \leq 3\)の整数という風に設定すればOKです。
しかし今回は1個目、2個目、3個目の満足度がそれぞれ異なるように設定したいので、上記のように設定するとうまくいきません。

そこで今回は1個目の変数を\(x_i\)、2個目の変数を\(y_i\)、3個目の変数を\(z_i\)と設定します。いずれも0-1変数にして、例えばお菓子1を2個買うときは\(x_1=y_1=1,\;z_1=0\)という風に設定します。
\(x_i \in \{0,1\}\)
\(y_i \in \{0,1\}\)
\(z_i \in \{0,1\}\)
\(i=1,2,…,20\)
変数の制約条件
実は変数を3つにするだけでは上手くいかないんです。例えば\(x_1,\;y_1\)の2つの変数について考えてみましょう。

\(x_1,\;y_1\)は0か1を取るので、合計4通りの組み合わせがあります。それぞれがどのような結果を表すのか見てみましょう。
\(x_1=y_1=0\)の場合はお菓子1を買わないということを表しています。
\(x_1=1,\;y_1=0\)の場合はお菓子1を1個だけ買うということを表しています。
\(x_1=y_1=1\)の場合はお菓子1を2個買うということを表しています。
では\(x_1=0,\;y_1=1\)の場合はどうでしょうか。1個目は買わずに2個目は買うなんてことは起こりません。この組み合わせは選択肢から除外する必要があるんです。
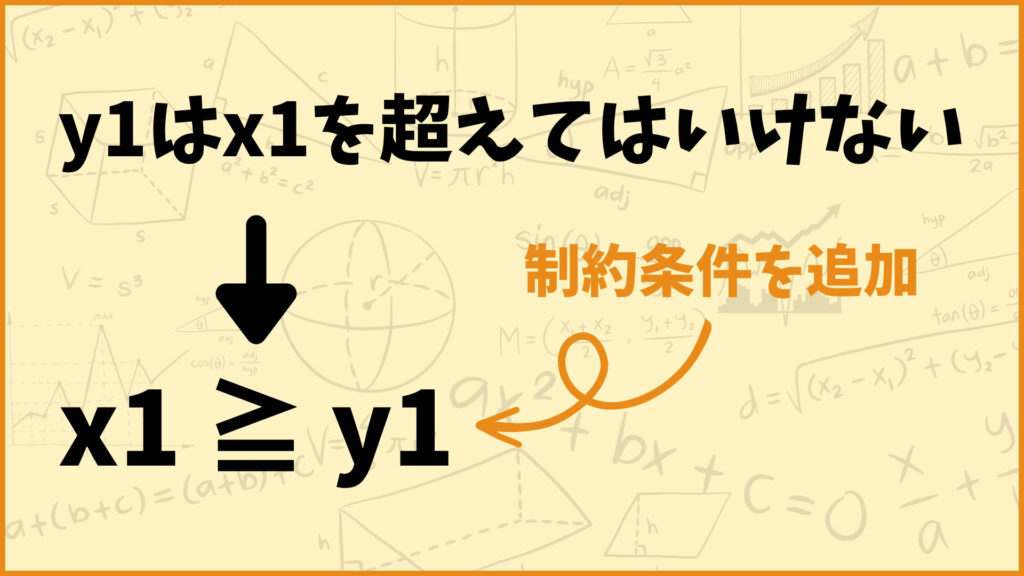
つまり\(y_1\)が\(x_1\)より大きくならないように設定すれば良いので、制約条件として\(x_1 \geq y_1\)を追加します。
\(y_1\)と\(z_1\)についても同じことが言えるので、制約条件として\(y_1 \geq z_1\)を追加する必要があります。
これらの話をまとめると、制約条件として\(x_1 \geq y_1 \geq z_1\)を追加することでお菓子1に関しては矛盾が無くなります。
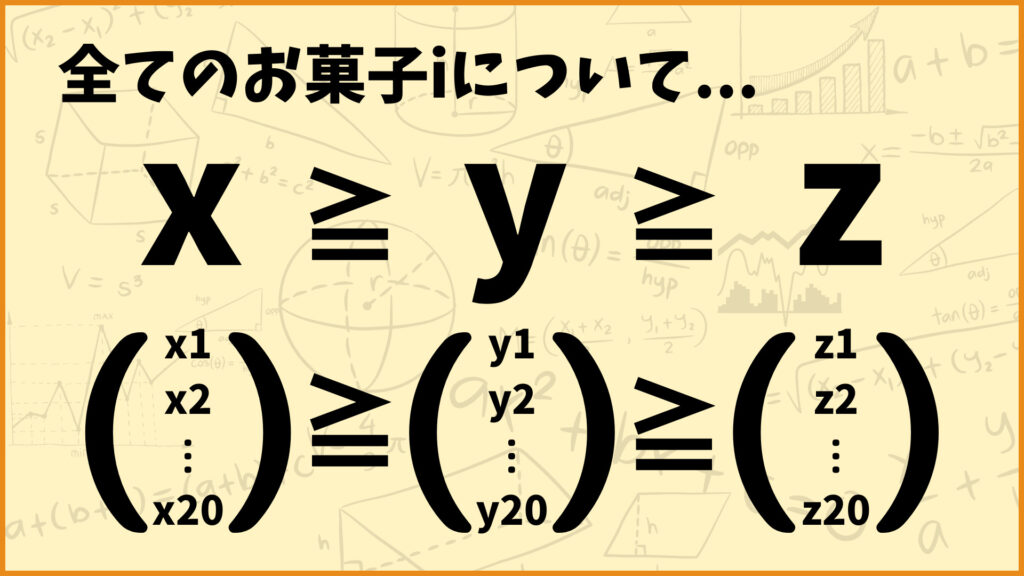
今の話をすべてのお菓子について考えます。つまりすべてのお菓子\(i\)について\(x_i \geq y_i \geq z_i\)が成り立つ必要があります。pythonでは変数ベクトル\(\boldsymbol{x},\;\boldsymbol{y},\;\boldsymbol{z}\)を使って、\(\boldsymbol{x} \geq \boldsymbol{y} \geq \boldsymbol{z}\)と表します。
\(x_i \geq y_i \geq z_i\)
\(i=1,2,…,20\)
予算の制約条件を設定する
次にこれらの変数を使って予算の制約条件を考えてみましょう。例えば変数が\(x_i\)しかない場合は、制約条件を以下のように表せます。
\(\sum\limits^{20}_{i=1}w_ix_i \leq 300\)
\(i=1,2,…,20\)
しかし今は変数の種類が3つあるので上記のままではうまくいきません。ちゃんと\(y_i,\;z_i\)も含めた予算制約を考える必要があります。
例えばお菓子1の値段が50円だとしましょう。

お菓子1を2個買うと値段の合計は\(50×2=100\)円となりますが、この2という数字は1個目を買って、2個目を買って、3個目は買わないというのを表しています。
変数で言うと\(x_1=1,\;y_1=1,\;z_1=0\)を表しています。そのため、お菓子1の値段の合計は変数\(x_1,\;y_1,\;z_1\)を使って\(50x_1+50y_1+50z_1\)という風に表すことができます。
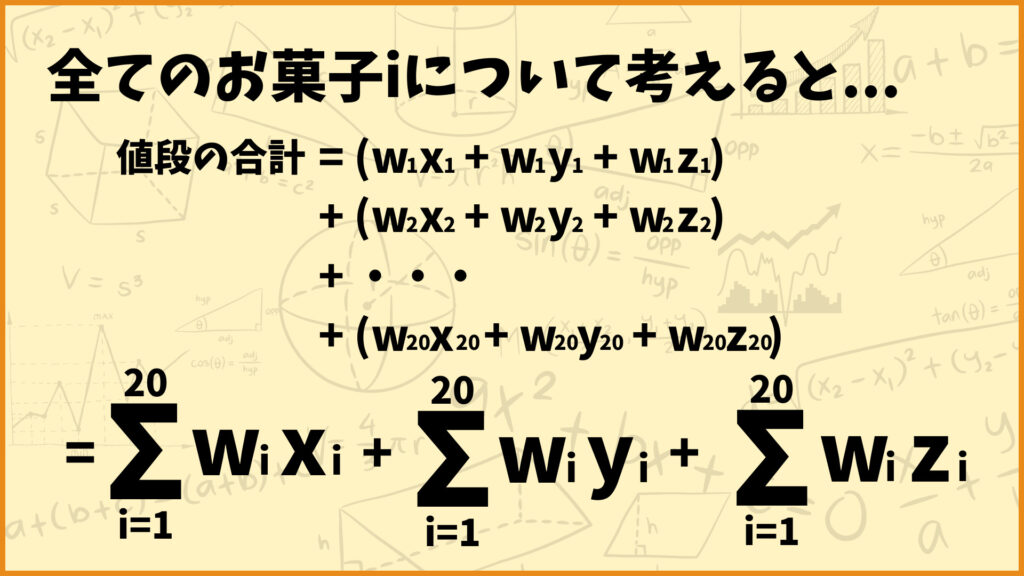
このことを一般化しましょう。お菓子\(i\)の1個当たりの値段を\(w_i\)として買い物をしたときの値段の合計は\((w_1x_1+w_1y_1+w_1z_1)+(w_2x_2+w_2y_2+w_2z_2)+…+(w_{20}x_{20}+w_{20}y_{20}+w_{20}z_{20})\)と表せます。
そしてこの式を変形して、見やすくすると\(\sum\limits^{20}_{i=1}w_ix_i+\sum\limits^{20}_{i=1}w_iy_i+\sum\limits^{20}_{i=1}w_iz_i\)と表せます。1つ目のシグマが1個目、2つ目のシグマが2個目、3つ目のシグマが3個目の値段をそれぞれ表しています。
それらを足すことで全部の値段の合計を式で表すことができます。そしてこの式が300円を超えないようにする必要があるので、全てをまとめると予算の制約条件は以下のように表せます。
\(\sum\limits^{20}_{i=1}w_ix_i+\sum\limits^{20}_{i=1}w_iy_i+\sum\limits^{20}_{i=1}w_iz_i \leq 300\)
目的関数を設定する
最後に目的関数を設定していきます。とはいっても予算制約と考え方はほぼ同じで、基本は重さ\(w_i\)を満足度\(v_i\)に変更すれば良いです。ただ問題なのが、2個目以降は満足度が\(\delta\)ずつ割り引かれることを考慮しないといけないです。
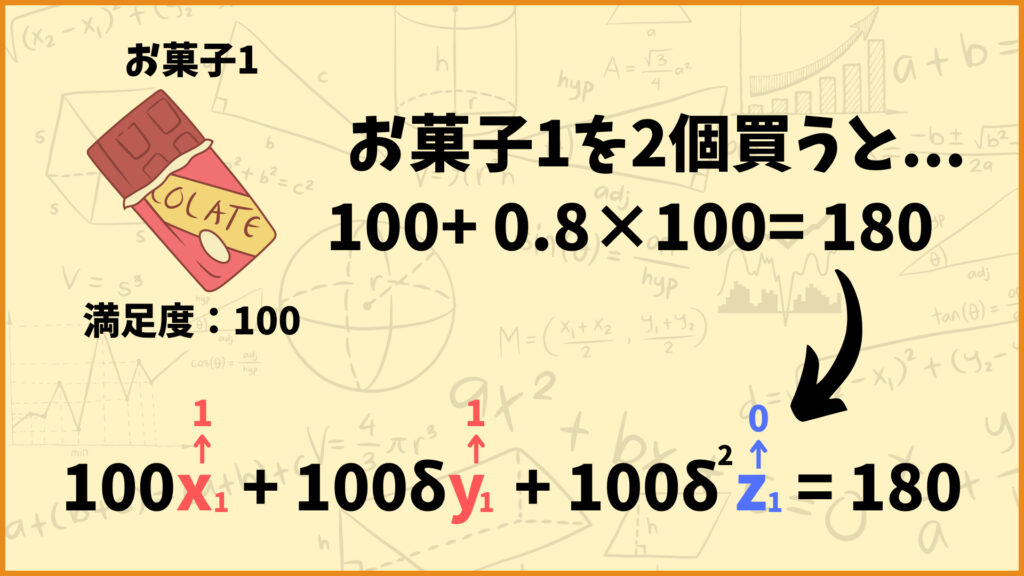
お菓子1の満足度が100、割引率が\(\delta=0.8\)場合を考えます。お菓子1を2個買うとその満足度は\(100+0.8×100=180\)となります。
変数で言うと\(x_1=1,\;y_1=1,\;z_1=0\)を表しています。そのため、お菓子1の値段の合計は変数\(x_1,\;y_1,\;z_1\)を使って\(100x_1+100\delta y_1+100\delta^2 z_1\)という風に表すことができます。

このことを一般化しましょう。お菓子\(i\)の1個当たりの満足度を\(v_i\)として買い物をしたときの値段の合計は\((v_1x_1+\delta v_1y_1+\delta^2 v_1z_1)+(v_2x_2+\delta v_2y_2+\delta^2 v_2z_2)+…\)
\(+(v_{20}x_{20}+\delta v_{20}y_{20}+\delta^2 v_{20}z_{20})\)と表せます。
そしてこの式を変形して、見やすくすると\(\sum\limits^{20}_{i=1}v_ix_i+\delta \sum\limits^{20}_{i=1}v_iy_i+\delta^2 \sum\limits^{20}_{i=1}v_iz_i\)と表せます。1つ目のシグマが1個目、2つ目のシグマが2個目、3つ目のシグマが3個目の満足度をそれぞれ表しています。
それらを足すことで全部の満足度の合計を式で表すことができます。この式を最大化することがこの問題の目的なので、全てをまとめると以下のように表せます。
\(\max{\sum\limits^{20}_{i=1}v_ix_i+\delta \sum\limits^{20}_{i=1}v_iy_i+\delta^2 \sum\limits^{20}_{i=1}v_iz_i}\)
今までの話を合わせて問題を定式化する
ここまでどうやって数式で表すかを長々と議論してきたので、最後にこれらの数式をまとめましょう。
\(\text{max}\;\;\;\sum\limits^{20}_{i=1}v_ix_i+\delta \sum\limits^{20}_{i=1}v_iy_i+\delta^2 \sum\limits^{20}_{i=1}v_iz_i\)
\(\text{s.t.}\;\;\;\;\;\sum\limits^{20}_{i=1}w_ix_i+\sum\limits^{20}_{i=1}w_iy_i+\sum\limits^{20}_{i=1}w_iz_i \leq 300\)
\(\;\;\;\;\;\;\;\;\;\;x_i \geq y_i \geq z_i\)
\(\;\;\;\;\;\;\;\;\;\;x_i \in \{0,1\}\)
\(\;\;\;\;\;\;\;\;\;\;y_i \in \{0,1\}\)
\(\;\;\;\;\;\;\;\;\;\;z_i \in \{0,1\}\)
\(\;\;\;\;\;\;\;\;\;\;i=1,2,…,20\)
ただし\(v_i\)はお菓子\(i\)の満足度、\(w_i\)はお菓子\(i\)の値段
pythonで実装してこの問題を解く
それでは最後にこの問題をpythonで実装して解いていきたいと思います。コードと結果自体は前回の記事で紹介しています!
前回の記事はこちらから見れます!
結論以下のコードを実行すれば上記の問題の最適解が得られます。
## ナップザック問題を解くための前準備
# pulpをインポート
! pip install pulp
from pulp import *
# pandasをインポート
import pandas as pd
# numpyをインポート
import numpy as np
# 満足度vをランダムに設定
np.random.seed(100)
v = np.random.randint(10, 100, 20)
# 価格wをランダムに設定
np.random.seed(200)
w = np.random.randint(10, 300, 20)
# 予算の上限を設定
capacity = 300
## ナップザック問題を設定して実際に解いてみる
# LpMaximizeで最大化に設定
prob = LpProblem(sense=LpMaximize)
# 変数の定義(まとめて定義)ここを変更する!!!!!!!!!!!!!!!!!!!!
x = [LpVariable(f"x{i}", cat = LpBinary) for i in range(1,21)]
y = [LpVariable(f"y{i}", cat = LpBinary) for i in range(1,21)]
z = [LpVariable(f"z{i}", cat = LpBinary) for i in range(1,21)]
# 割引率の設定 ここを変更する!!!!!!!!!!!!!!!!!!!!!!!!!!!!
delta = 0.5
# 問題の設定
# 目的関数を設定 ここを変更する!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
prob += lpDot(v, x) + (delta*lpDot(v, y)) + (delta**2*lpDot(v, z))
# 制約条件を設定 ここを変更する!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
prob += lpDot(w, x) + lpDot(w, y) + lpDot(w, z) <= capacity
prob += x >= y >= z
prob.solve() # 問題を解く
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示
# 各お菓子の購入個数をデータフレームで表示
x_val = np.array([value(x[i]) for i in range(20)])
y_val = np.array([value(y[i]) for i in range(20)])
z_val = np.array([value(z[i]) for i in range(20)])
df = pd.DataFrame(data=x_val+y_val+z_val, index = [f"お菓子{i}" for i in range(1,21)],columns=["購入個数"])
df
それでは上記のコードを解説していきます。基本的な構造は前回の記事で紹介した、デフォルトの問題を解くコードと同じなので、今回は「ここを変更する!!!!」ってところと結果の表示の所を説明します。
変数の定義
# 変数の定義(まとめて定義)ここを変更する!!!!!!!!!!!!!!!!!!!!
x = [LpVariable(f"x{i}", cat = LpBinary) for i in range(1,21)]
y = [LpVariable(f"y{i}", cat = LpBinary) for i in range(1,21)]
z = [LpVariable(f"z{i}", cat = LpBinary) for i in range(1,21)]24~27行目で変数の定義をしています。変数はリストで表しました。LpVariableで変数を作成します。LpBinaryで0-1変数に指定します。
割引率の定義
# 割引率の設定 ここを変更する!!!!!!!!!!!!!!!!!!!!!!!!!!!!
delta = 0.528~29行目で割引率を設定しています。今回は0.5で設定しました。1個目でかなり満足しちゃうタイプの子を想定しています。
目的関数を設定
# 目的関数を設定 ここを変更する!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
prob += lpDot(v, x) + (delta*lpDot(v, y)) + (delta**2*lpDot(v, z))32~33行目で目的関数を設定しています。lpDot(v,x)は\(\sum\limits^n_{i=1}v_ix_i\)を表しています。\(y\)と\(z\)に関しては割引率を掛け算する必要があるのでさっき定義した\(\delta\)と\(\delta^2\)を掛けています。
制約条件を設定
# 制約条件を設定 ここを変更する!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
prob += lpDot(w, x) + lpDot(w, y) + lpDot(w, z) <= capacity
prob += x >= y >= z 35行目は予算制約を表しています。目的関数のときに説明したlpDotをここでも使ってます。36行目は変数の制約条件を表しています。
結果を表示
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示
# 各お菓子の購入個数をデータフレームで表示
x_val = np.array([value(x[i]) for i in range(20)])
y_val = np.array([value(y[i]) for i in range(20)])
z_val = np.array([value(z[i]) for i in range(20)])
df = pd.DataFrame(data=x_val+y_val+z_val, index = [f"お菓子{i}" for i in range(1,21)],columns=["購入個数"])
df普通に\(x_i,\;y_i,\;z_i\)の値を表示させても良いんですけどかなり見づらいのでデータフレーム形式にして表してみました。
\(x_i\)の値はvalue(x[i])で求められます。今回は\(i=1,2,…,20\)に対して\(x_i\)の値を求め、numpyのarrayを使った配列にx_valと名前をつけて保存しています。同じようにy_valは\(y_i\)の配列, z_valは\(z_i\)の配列となっています。
47行目で先ほど作った配列たちをまとめてデータフレームにしています。データはx_val+y_val+z_valにしているので、データフレームの各要素はそのお菓子を何個買ったかを表しています。
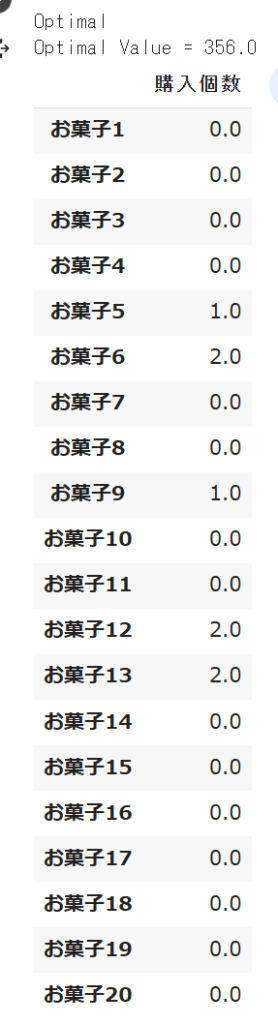
このコードを出力した結果、上記のようなデータフレームが出力されます。Optimalと表示されているのでちゃんと最適解が求められています。
Optimal Valueは最適値を表しており、今回の問題は満足度の最大値が356であることを表しています。その下は各お菓子の購入個数を表しています。
これを見るとお菓子6、12、13を2個、お菓子5、9を1個買うのがもっとも満足度が高いようです。さすがに3個目買うと元の満足度の\(\frac{1}{4}\)になるので選ばれないようですね。
おわりに
いかがでしたか。
今回の記事ではナップサック問題について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました