こんにちは!しゅんです!
今回は整数計画問題として定式化してアルバイトのシフト作成をしていきたいと思います!
シフトを作成するのって色々制約があって大変ですよね。この記事では条件を全て満たし、かつみんなが納得するようなシフト作成の方法を解説していきます!
このテーマは
・結果の解釈
・問題の設定と定式化の解説 ← 今回はここ!
・pythonで実装する方法の解説
の3つの記事に分かれています!
結果の解釈はこちらから!
pythonで実装する方法はこちらから!
それでは解説していきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
整数計画問題として問題を作成
この記事ではシフト作成問題を整数計画問題として、目的関数と制約条件を設定したいと思います。簡単に言うと変数が取りうる値が整数の問題です。
整数計画問題としてはナップサック問題が有名です。
ナップサック問題はこちらの記事で説明しています!

それでは1つずつ解説していきましょう!
問題設定を決める
まず最初に今回考える問題を設定していきます。今回は以下のように問題を設定したいと思います。
今回考える問題
・あるアルバイトの1週間分のシフトを決める。(このシフトは1カ月使う)
・アルバイトの希望賃金との差がなるべく小さくなるようにシフトを作る
・アルバイト生は合計16人である。
・シフトの種類は日勤(d)、準夜勤(e)、深夜勤(n)の3つがある。
・各シフトの情報は以下の通りである。

制約条件を決める
次に考慮しなければいけない条件を設定します。まず最初に列挙してその後1つずつ解説していきます。
考慮する制約条件
・各シフトには必要人数しか入れない
・1日のシフトは最大1つまで
・深夜勤→日勤、深夜勤→準夜勤、準夜勤→日勤は禁止
・1週間のシフト数は最大5個まで
・深夜勤は最大3連勤まで
各シフトには必要人数しか入らない
例えば日勤のシフトは必要人数が4人ですが、そこに10人も入れたら訳が分からない状態になりますね。逆に4人必要なのに2人しか入っていなかったら人手が足りなくて忙しくなってしまいます。
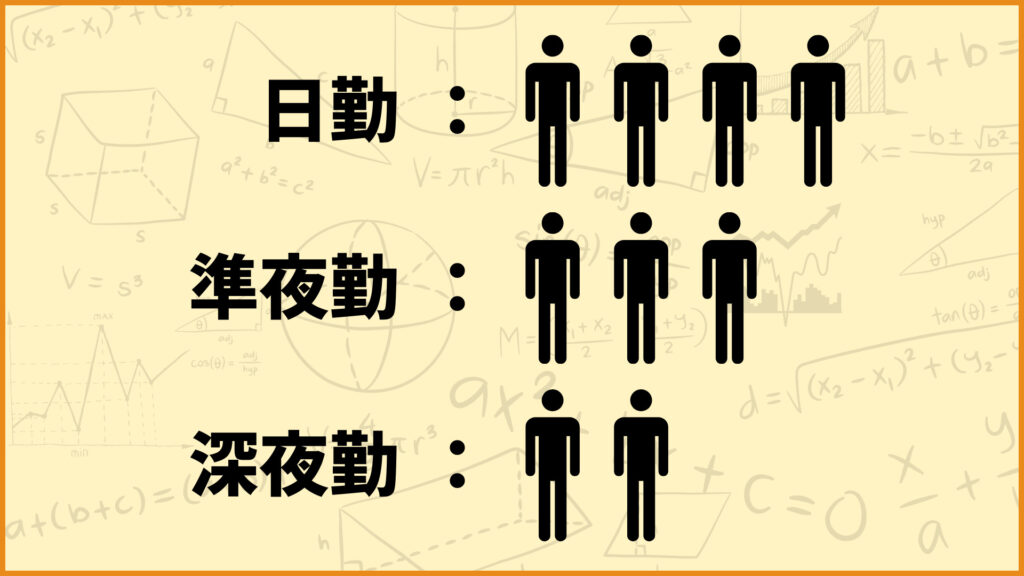
なので日勤は4人、準夜勤は3人、深夜勤2人ぴったりになるように配属する必要があります。
1日のシフトは最大1つまで
例えば8:00~16:00まで日勤でバイトした後、続けて準夜勤、夜勤をすることを禁止します。また準夜勤でバイトしたときはその日の日勤と深夜勤はできません。さらに深夜勤でバイトしたときはその日の日勤と準夜勤はできません。
深夜勤は24:00~8:00なので時間的には次の日になりますが、ここでは日勤、準夜勤、深夜勤を1日のシフトの集合として考えています。

深夜勤→日勤、深夜勤→準夜勤、準夜勤→日勤は禁止
これも働きすぎを制限する条件です。


※準夜勤→深夜勤は「1日のシフトは最大1つまで」で制限しています。
1週間のシフト数は最大5個まで
これは何連勤もするのを防ぐための条件です。

6回働いてしまうと、どう頑張っても6連勤になってしまうのでそれは禁止します。
深夜勤は最大3連勤まで
最大でも深夜勤は3連勤までにします。4連勤でなければ1週間に4回以上深夜勤しても大丈夫です。

これらの条件を数式を使って表していきたいと思います。
集合の定義
それではこの問題を数式で表すためにまず集合から定義していきましょう。今回は3つの集合を以下のように定義します。
\(P=\{1,2,…,16\}\):アルバイト生\(i\)の集合
\(D=\{1,2,…,7\}\):曜日\(j\)の集合
\(S=\{d,e,n\}\):シフト\(k\)の集合
まず\(P\)はアルバイト生の集合で、16人いるのでそれぞれに数字でラベル付けをしています。\(D\)は曜日の集合で1が月曜、2が火曜、…、7が日曜を表します。\(S\)はシフトの集合で\(d\)が日勤、\(e\)が準夜勤、\(n\)が深夜勤を表しています。
パラメータの定義
次にパラメータの定義をしていきます。今回は各シフトの賃金と、各アルバイト生の希望賃金を定義します。
\(w_k \; (k \in S)\):シフト\(k\)の時給
\(np_k \; (k \in S)\) : シフト\(k\)での必要人数
\(e_i \; (i \in P)\):アルバイト生\(i\)の希望賃金
\(w_k\)はシフト\(k\)の時給を表しています。例えば\(k=d\)(日勤)の場合は\(w_d=1000\)という風になります。
\(np_k\)はシフト\(k\)で必要とされる人数です。例えば\(k=d\)(日勤)の場合は\(np_d=4\)という風になります。
\(e_i\)はアルバイト生\(i\)が希望する賃金を表しています。今回はこの希望賃金と実際に作られたシフトで得られる賃金の差がなるべく小さくなるようなシフトを作成していきます。
変数の定義
それでは変数を設定していきましょう。今回は0-1変数の\(x_{ijk}\)を使いたいと思います。\(x_{ijk}\)はアルバイト生\(i\)が\(j\)曜日にシフト\(k\)に入るなら1、入らないなら0を取るような変数です。

目的関数の設定
次に目的関数を設定します。今回は「アルバイト生の希望賃金との差をなるべく小さくする」ことが目的です。これをどのように目的関数として表すかを考えてみます。
目的関数の候補1
一番簡単な表現は、全てのアルバイト生に対して希望賃金と作成されたシフトによって得られる賃金との差の二乗を足すことだと思います。
\(\sum\limits_{i \in P}( e_i – \sum\limits_{j \in D k \in S} 8w_kx_{ijk})^2\)
\(\sum\limits_{j \in D k \in S} 8w_kx_{ijk}\)はアルバイト生\(i\)が1週間で稼ぐ金額です。(8を掛けてるのはそれぞれのシフトでは8時間働くからです。)
しかしこの目的関数だと変数の2乗がでてきてしまい、線形関数ではなくなります。それに一人のバイト生だけにしわ寄せがいってしまう可能性があります。

例えばバイト生が3人で、希望賃金との差がそれぞれ0, 100, 0の場合と60, 60, 60の場合を考えます。このとき目的関数の値は、前者が10000で後者が11200となります。
このような場合、全員で負担するよりも一人に負担させた方が良いシフトだと判断されるので、結果的に不満が出るシフトが作成される可能性があります。あまり得策ではなさそうです。
目的関数の候補2
上の問題を解決するために、希望賃金との差が一番大きい人の差(絶対値)がなるべく小さくなるように設定します。
すなわち\(\max_\limits{i \in P}|e_i-\sum\limits_{j \in D k \in S} 8w_kx_{ijk}|\)で希望賃金との差が最大のものを求めて、これを最小化するというのを目的関数にします。
\(\text{min}\max\limits_{i \in P}|e_i-\sum\limits_{j \in D k \in S} 8w_kx_{ijk}|\)
ということで目的関数をミニマックス問題として定式化できました。ただこのままだと解けないので、以下のように変形することで混合整数最適化問題にすることができます。
\(\text{min}\;\;\;t\)
\(\text{s.t.}\;\;\;|e_i-\sum\limits_{j \in D k \in S} 8w_kx_{ijk}| \leq t\)
差の絶対値を\(t\)で抑えて、この\(t\)を最小化するようにします。絶対値がめんどくさいので2つの式に分解しましょう。
\(\text{min}\;\;\;t\)
\(\text{s.t.}\;\;\;\sum\limits_{j \in D k \in S} 8w_kx_{ijk}-e_i \leq t\)
\(\;\;\;\;\;\;\;\;\;\;e_i – \sum\limits_{j \in D k \in S} 8w_kx_{ijk} \leq t\)
今回はこれを目的関数とします。(制約条件も入ってますが笑)
制約条件の設定
それでは最後に制約条件を設定しましょう。順を追って一つずつ解説していきます。
各シフトには必要人数しか入らない
例えば月曜日の日勤について考えてみましょう。

バイト生\(i\)が月曜日に日勤に入るかどうかの変数は\(x_{i11}\)で表せます。例えばバイト3が月曜日の日勤に入るなら\(x_{311}=1\)となります。
この制約条件を満たすためには\(x_{i11}\)を\(i=1,2,…16\)まで足したら4になってないといけないですね。
もしこの合計が5だったら月曜日の日勤に5人入ることになってしまいます!
これを一般化しましょう。シフト\(k\)の必要人数は\(np_k\)で与えられているので、全ての\(j,k\)について、\(j\)曜日のシフト\(k\)の\(x_{ijk}\)を\(i=1,2,…,16\)まで足すと、その合計が必ず\(np_k\)になる必要があります。
これを式にすると以下のようになります。
\(\sum\limits_{i \in P}x_{ijk}=np_k\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; j \in D,\; k \in S\)
1日のシフトは最大1つまで
今度は月曜日にバイト1がシフトに入るかどうかを考えます。

バイト1が月曜日の日勤に入るなら\(x_{11d}=1\)となります。ここで、バイト1が日勤に入るなら月曜日の準夜勤と深夜勤には入ることができません。すなわち\(x_{11k}\)を\(k \in \{d,e,n\}\)全て足したときの合計が1以下になっている必要があります。
合計が2だと日勤と準夜勤の両方や日勤と深夜勤の両方に割り当てられる可能性があります。
また合計が0の場合は、バイト1が月曜日のどのシフトにも入らないことを表しているので不等号を使っても問題ないです。
これを一般化しましょう。すべてのバイト生\(i\)、全ての曜日\(j\)に対して\(x_{ijk}\)を\(k \in \{d,e,n\}\)全て足したときの合計が1以下になっている必要があります。
これを式にすると以下のようになります。
\(\sum\limits_{k \in S}x_{ijk} \leq 1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; i \in P, \; j \in D\)
深夜勤→日勤、深夜勤→準夜勤、準夜勤→日勤は禁止
まずは準夜勤→日勤について考えてみましょう。例えばバイト生1が月曜日に準夜勤をしたとします。

バイト生1が月曜日に準夜勤をするのは\(x_{11e}=1\)で表せます。このときバイト生1は火曜日に日勤ができません。つまり\(x_{12d}=0\)となる必要があります。
つまりこの2つの変数が両方とも1となる場合を禁止すれば良いので
\(x_{11e}+x_{12d} \leq 1\)という風に表せます。
どっちかの変数が1になる場合及びどっちの変数も0になる場合はOKなので、両方が1になる場合だけを禁止するような不等式を作れば大丈夫です。

このことを一般化しましょう。バイト生\(i\)が\(j\)曜日に準夜勤\(e\)をしたときに、\(j+1\)曜日に日勤\(d\)をすることを禁止する制約条件は\(x_{ije}+x_{i(j+1)d} \leq 1\)と表せそうです。
しかしこのままでは1つ問題が生じてしまいまいます。それは日曜日と月曜日の制約をどうすれば良いかという問題です。

日曜日のことを考えたければ\(j=7\)を代入すれば良いです。しかしこの場合\(j+1=8\)となってしまいます。月曜日は1で表されるので、これでは日曜日に準夜勤をすると次の日(月曜日)は日勤ができないという場合を禁止できません。
これを解決するために、7で割った余りを導入しましょう。もし\(j+1=8\)のときは\(j+1 \equiv 1 \; (\text{mod} \; 7)\)となり、ちゃんと月曜日を表すことができます。
今回は\((j+1)_{\text{mod}7}\)を「\(j+1\)を7で割ったときの余り」という意味で使っています。
\(a \equiv b \; (\text{mod} \; m)\)は合同式と呼ばれ、「\(a\)を\(m\)で割った余りと\(b\)を\(m\)で割った余りが等しい」ということを表しています。
深夜勤→準夜勤と深夜勤→日勤も同じように考えると、最終的に以下のように制約条件を定式化できます。
\(x_{ije}+x_{i(j+1)_{\text{mod}7}d} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
\(x_{ijn}+x_{i(j+1)_{\text{mod}7}d} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
\(x_{ijn}+x_{i(j+1)_{\text{mod}7}e} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
1週間のシフト数は最大5個まで
例えばバイト1の1週間のシフト数について考えてみましょう。バイト1が\(j\)曜日のシフト\(k\)に入るかどうかは\(x_{1jk}\)が0か1かで判断します。

従って\(j=1,2,…,7\)及び\(k \in \{d,e,n\}\)に対して\(x_{1jk}\)を全て足した和が5以下になる必要があります。これを一般化すると、全てのバイト生\(i\)に対して上の条件が成り立つ必要があります。
以上のことを式にすると以下のようになります。
\(\sum\limits_{j \in D,k \in S}x_{ijk} \leq 5 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; i \in P\)
深夜勤は最大3連勤まで
最後に深夜勤の連勤に関する制約を定式化しましょう。これもバイト生1を例に考えてみましょう。

バイト生1が月火水に深夜勤をする場合は木曜日には深夜勤はできません。つまり\(x_{11n}=x_{12n}=x_{13n}=1\)のときは\(x_{14n}=0\)となる必要があります。
このことを数式で表すと\(x_{11n}+x_{12n}+x_{13n}+x_{14n} \leq 3\)となります。
簡単に言うと4つの変数が全て1になることを防ぐような式を作ればOKです。

このことをより一般化すると、バイト生\(i\)が曜日\(j,j+1,j+2\)に深夜勤\(n\)に入る場合は曜日\(j+3\)に深夜勤に入れないというのを式にすると、
\(x_{ijn}+x_{i(j+1)n}+x_{i(j+2)n}+x_{i(j+3)n} \leq 3\)となりそうです。
しかしこの場合もやはり曜日の範囲で問題が生じます。例えば\(j=5\)のとき\(j+3=8\)となり、上限の7を超えてしまいます。
そのためこれもmod 7で考えましょう。以上のことをまとめるとこの条件は以下のように表せます。
\(x_{ijn}+x_{i(j+1)_{\text{mod}7}n}+x_{i(j+2)_{\text{mod}7}n}+x_{i(j+3)_{\text{mod}7}n} \leq 3\;\;\;\;\;i \in P,\; j \in D\)
これまでのことをまとめて問題を数式で表す
最後にこれまで話してきたことをまとめて、今回の問題を数式で表します。
\(P=\{1,2,…,16\}\):アルバイト生\(i\)の集合
\(D=\{1,2,…,7\}\):曜日\(j\)の集合
\(S=\{d,e,n\}\):シフト\(k\)の集合
\(w_k \; (k \in S)\):シフト\(k\)の時給
\(np_k \; (k \in S)\) : シフト\(k\)での必要人数
\(e_i \; (i \in P)\):アルバイト生\(i\)の希望賃金
\(\text{min} \;\;\;\;\;\;t\)
\(\text{s.t.}\;\;\sum\limits_{j \in D,k \in S}8w_kx_{ijk}-e_i \leq t\;\;\;\;\; i \in P\)
\(\;\;\;\;\;\;\;e_i-\sum\limits_{j \in D,k \in S}8w_kx_{ijk} \leq t\;\;\;\;\; i \in P\)
\(\;\;\;\;\;\;\;\sum\limits_{i \in P}x_{ijk}=np_k\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; j \in D,\; k \in S\)
\(\;\;\;\;\;\;\;\sum\limits_{k \in S}x_{ijk} \leq 1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; i \in P, \; j \in D\)
\(\;\;\;\;\;\;\;x_{ije}+x_{i(j+1)_{\text{mod}7}d} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
\(\;\;\;\;\;\;\;x_{ijn}+x_{i(j+1)_{\text{mod}7}d} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
\(\;\;\;\;\;\;\;x_{ijn}+x_{i(j+1)_{\text{mod}7}e} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
\(\;\;\;\;\;\;\;\sum\limits_{j \in D,k \in S}x_{ijk} \leq 5 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; i \in P\)
\(x_{ijn}+x_{i(j+1)_{\text{mod}7}n}+x_{i(j+2)_{\text{mod}7}n}+x_{i(j+3)_{\text{mod}7}n} \leq 3\;\;\;\;\;i \in P,\; j \in D\)
おわりに
いかがでしたか。
今回の記事ではシフト作成問題の数式について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。