こんにちは!しゅんです!
今回の記事ではなぜクラスカル法で最小全域木が求まるのかを説明していきたいと思います!
クラスカル法はグラフ理論で登場する用語で、重み付きグラフの最小全域木を見つけるためのアルゴリズムの一つです。
クラスカル法を使って最小全域木を求める手順は下の記事で解説しています!
↓↓↓クラスカル法のアニメーション↓↓↓
それでは解説していきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
証明したいこと
今回は以下の定理を証明することによってクラスカル法で最小全域木が求められることを示したいと思います。
全域木\(T^*\)が最小全域木である \(\Longleftrightarrow\) 全域木\(T^*\)が条件Aを満たす。
条件A:
\(T^*\)に含まれない全ての辺\((u,v)\)に対して、頂点\(u\)と頂点\(v\)を繋ぐパス\(p\)が\(T^*\)中に存在し、さらにパス\(p\)中の全ての辺\((x,y)\)に対して\(c(u,v) \geq c(x,y)\)が成立する。
但し\(c(u,v)\)は辺\((u,v)\)の重み
文字で説明するだけじゃ分かりづらいので実際のグラフを使って条件Aを説明していきます。
条件Aが言っていること
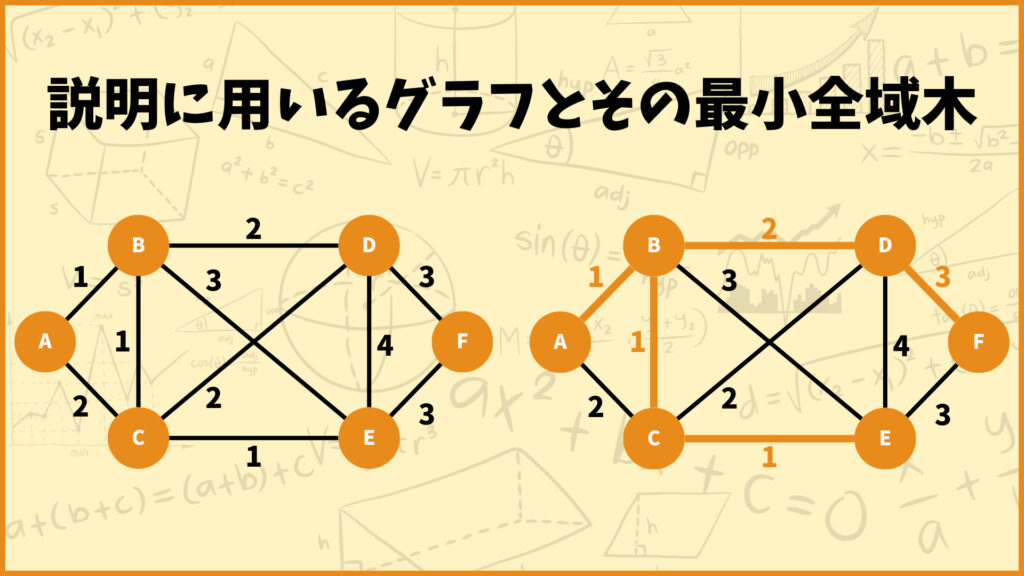
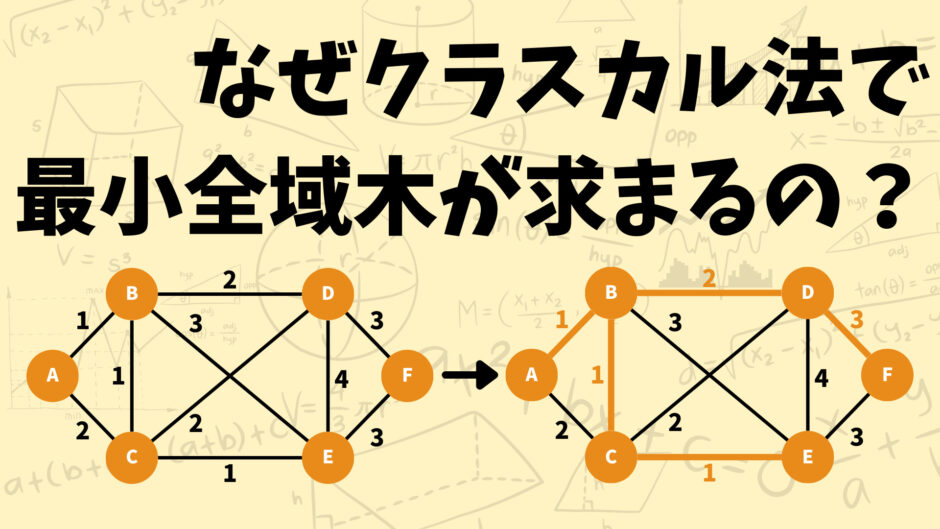
上のグラフとその最小全域木を使って条件Aを説明していきます。まず最小全域木\(T^*\)に含まれない辺\((u,v)\)について考えます。
例えば上の例で言うと、オレンジの太線になっていない辺(C,D)、辺(B,E)、辺(A,C)、辺(D,E)、辺(E,F)が\(T^*\)に含まれない辺に該当します。試しに辺(C,D)について考えてみましょう。
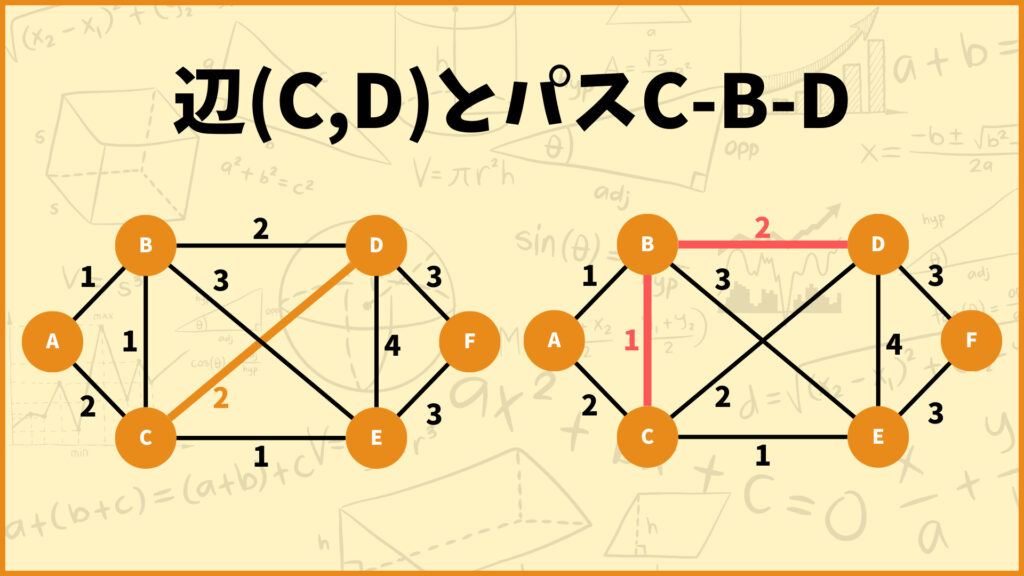
条件Aを見てみると辺(C,D)が\(T^*\)に含まれていないとき、頂点Cと頂点Dを繋ぐパス\(p\)が\(T^*\)中に存在すると言っています。今回はパス\(p\)としてC-B-Dがちゃんと存在しています。
次にパス\(p\)中の辺\((x,y)\)との辺の重みを比べてみます。条件Aを見てみると、パス\(p\)中の全ての辺\((x,y)\)に対して\(c(u,v) \geq c(x,y)\)、つまり辺\((u,v)\)の重みは辺\((x,y)\)の重み以上であると言っています。
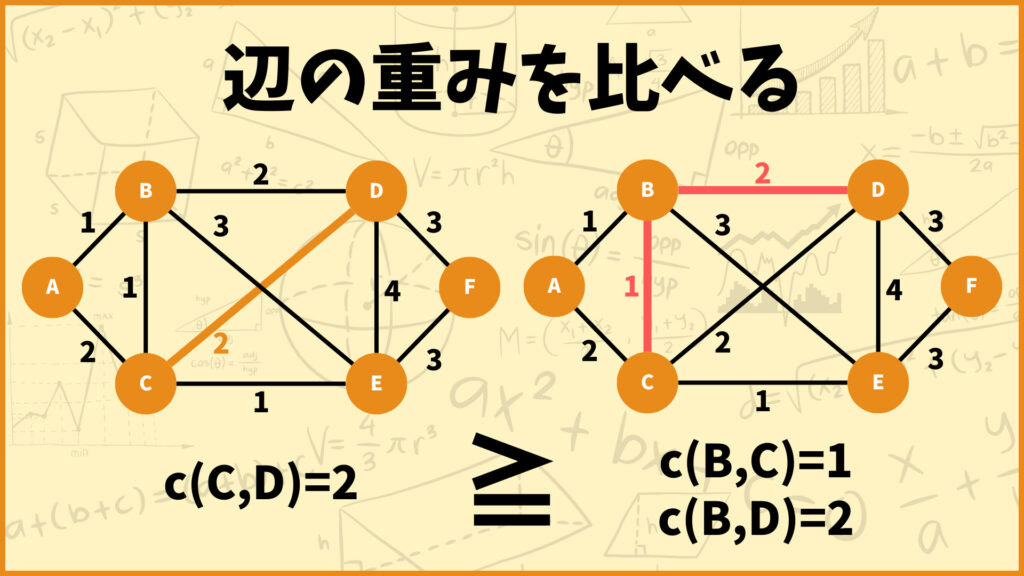
上のグラフの例で言うと辺(C,D)の重みは\(c(C,D)=2\)でパスC-B-D中の辺\((B,C), \; (B,D)\)の重みはそれぞれ\(c(B,C)=1, \; c(B,D)=2\)となっています。
左が\(c(u,v)\)で右の2つが\(c(x,y)\)なので、つまりパスC-B-D中の全ての辺\((x,y)\)に対して\(c(u,v) \geq c(x,y)\)がちゃんと成り立っています。
ということで辺(C,D)に関しては条件Aがちゃんと成立していることが分かりました。これが\(T^*\)に含まれない全ての辺で成り立っていると言っているのが条件Aです。
クラスカル法は条件Aが必ず成り立つような辺の選び方をしている
一旦上の定理が成り立つと思ってクラスカル法を考えていきます。クラスカル法の手順をおさらいしましょう。
- 重みが小さい順に辺\(e_1,\; e_2,\; …, \; e_m\)を並べる。
(\(c(e_1) \leq c(e_2) \leq …\leq c(e_m)\):\(c(e_i)\)は辺\(e_i\)の重み) - \(T=\emptyset\)とする。
- \(i=1,2,…,m\)に対して
もし\(T \cup e_i\)が閉路を持たないなら\(T\)に辺\(e_i\)を追加する。 - \(T\)を出力する。
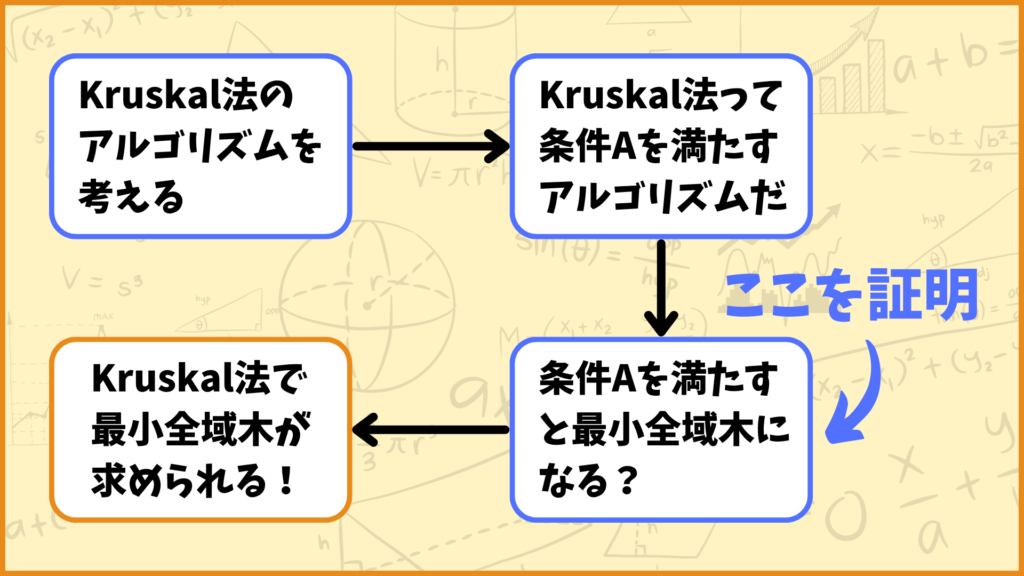
簡単に言うとクラスカル法は閉路ができないように重みが小さい順に辺を選んでいくという方法です。重みが小さい順に辺を選んでいるので、このようにして得られた全域木\(T^*\)は条件Aを満たしているはずです。

すなわち仮にあの定理が成り立つことが証明出来たらクラスカル法で最小全域木が求められることも示せるということです。
定理を証明する
それではいよいよあの定理を証明したいと思います。もう一度下に証明したい定理をおさらいおきます。
全域木\(T^*\)が最小全域木である \(\Longleftrightarrow\) 全域木\(T^*\)が条件Aを満たす。
条件A:
\(T^*\)に含まれない全ての辺\((u,v)\)に対して、頂点\(u\)と頂点\(v\)を繋ぐパス\(p\)が\(T^*\)中に存在し、さらにパス\(p\)中の全ての辺\((x,y)\)に対して\(c(u,v) \geq c(x,y)\)が成立する。
但し\(c(u,v)\)は辺\((u,v)\)の重み
この定理は必要十分条件\((\Longleftrightarrow)\)なので、十分条件\((\Rightarrow)\)と必要条件\((\Leftarrow)\)の2つをそれぞれ証明していく必要があります。
十分条件\((\Rightarrow)\)の証明
「全域木\(T^*\)が最小全域木\(\Rightarrow\)条件Aを満たす」を証明します。
背理法で証明します。パス\(p\)(\(u-v\)路)中のある辺\((x,y)\)に対して、\(c(u,v)<c(x,y)\)が成り立つと仮定します。
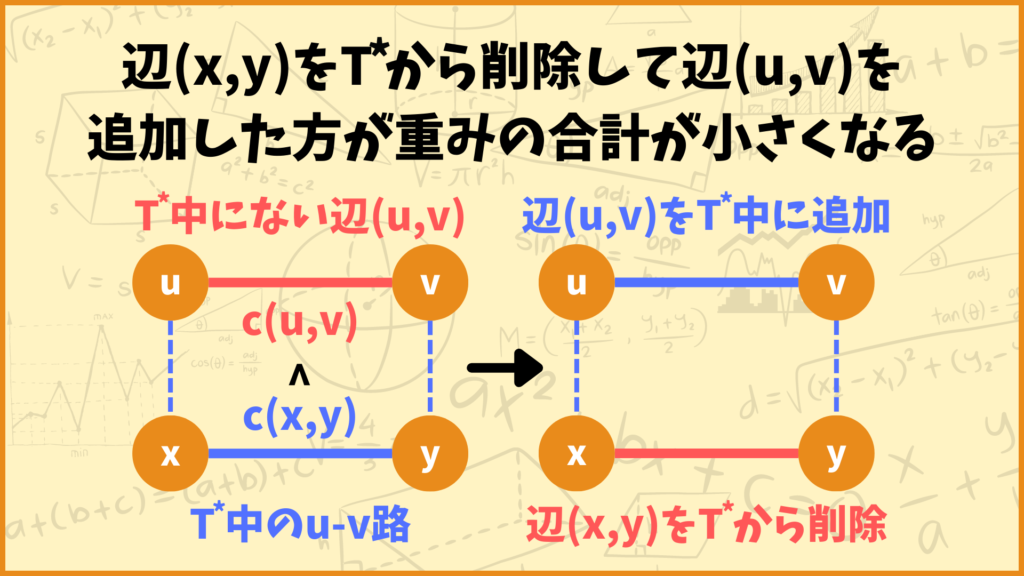
このとき\(T’\)を\(T^*\)から辺\((x,y)\)を除いて辺\((u,v)\)を加えたもの、すなわち\(T’=(T^*\backslash (x,y)) \cup (u,v)\)とすると、\(T’\)は\(T^*\)よりも重みの合計が小さい最小全域木となります。
しかしこれは\(T^*\)が最小全域木であることに矛盾します。ということで十分条件\((\Rightarrow)\)が証明できました。
必要条件\((\Leftarrow)\)の証明
十分条件は簡単に示せましたが必要条件を示すのは結構大変なので、1つずつ説明していきます。今\(T^*\)が条件Aを満たすとします。すなわち下の条件が成り立っているとします。
全域木\(T^*\)に含まれない全ての辺\((u,v)\)に対して、頂点\(u\)と頂点\(v\)を繋ぐパス\(p\)が\(T^*\)中に存在し、さらにパス\(p\)中の全ての辺\((x,y)\)に対して\(c(u,v) \geq c(x,y)\)が成立する。
但し\(c(u,v)\)は辺\((u,v)\)の重み
十分条件も背理法で証明したいと思います。今\(T’\)を\(T^*\)と最も多くの辺を共有する最小全域木と仮定します。(ただし\(T’ \ne T^*\))

ここからは以下の条件Bを満たす\(T^*\)中の辺\((u,v)\)が存在することを証明します。
条件B :
頂点\(u\)と頂点\(v\)を結ぶ\(T’\)中のパス\(p\)が、\(c(x,y) \geq c(u,v)\)を満たす辺\((x,y)\)を含む。
もしこの条件を満たす辺\((u,v)\)が存在すれば、\(T’\)から辺\((x,y)\)を除いて辺\((u,v)\)を追加したグラフ、すなわち\((T’ \backslash (x,y)) \cup (u,v)\)は最小全域木になります。
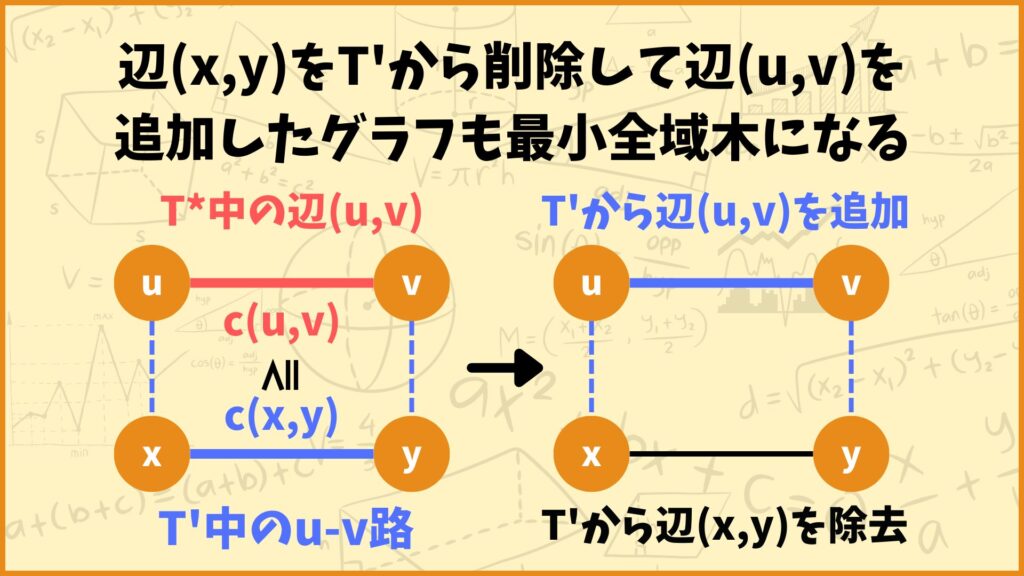
新しくできた最小全域木と\(T^*\)との共有辺の数を考えると、辺\((u,v)\)が\(T^*\)に含まれているので\(T’\)と\(T^*\)との共有辺の数よりも1個多くなります。
ところが\(T’\)は\(T^*\)と最も辺を多く共有する最小全域木だったので、これに矛盾します。したがって必要条件\((\Leftarrow)\)が示せるというわけです。
話がややこしくなりましたが、つまり条件Bを満たす\(T^*\)中の辺\((u,v)\)が存在することを証明すれば必要条件\((\Leftarrow)\)も示せるということです。
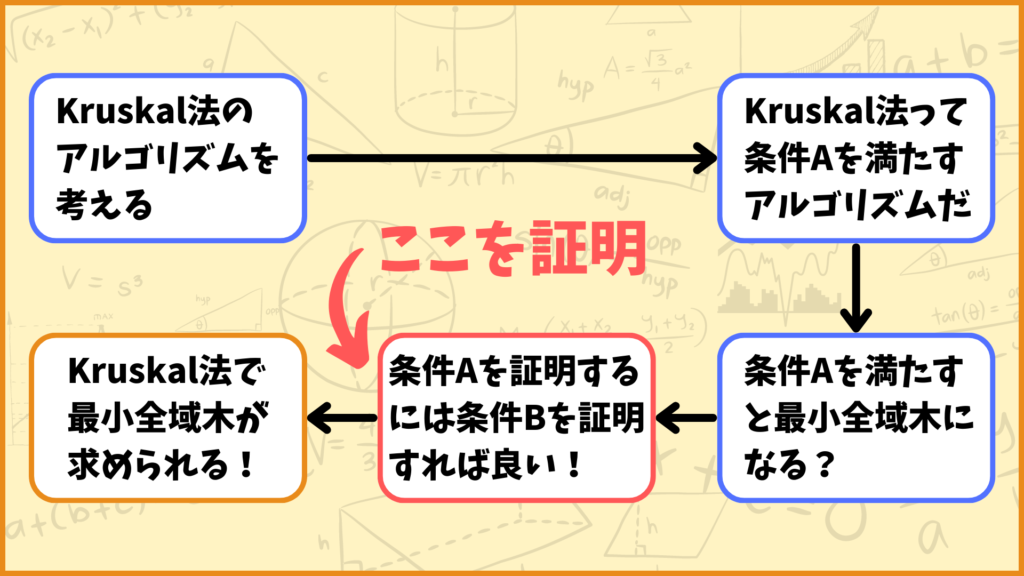
条件Bを満たす辺が存在することの証明
それでは最後に条件Bを満たす\(T^*\)中の辺\((u,v)\)が存在することを証明していきます。
頂点\(u\)と頂点\(v\)を結ぶ\(T’\)中のパス\(p\)が、\(c(x,y) \geq c(u,v)\)を満たす辺\((x,y)\)を含む。
これも背理法で証明していきます。条件Bを満たす\(T^*\)中の辺\((u,v)\)が存在しないと仮定して矛盾を導きます。
今、\(T^*\)中にあって\(T’\)中にはない辺\((u_1,v_1)\)を考えます。\(T’\)は最小全域木なので\(u_1 – v_1\)路が存在しますが、辺\((u_1,v_1)\)がありません。(\((u_1,v_1) \in T^* \backslash T’\)だから)
したがって\(T’\)中の\(u_1 -v_1\)路には\(T^*\)にない辺\((x_1,y_1)\)が存在します。
「\(T’\)中の\(u_1 -v_1\)路には\(T^*\)にない辺\((x_1,y_1)\)が存在する」と断言できるのは、もし仮に\(u_1-v_1\)路中の全ての辺が\(T^*\)中の辺だった場合\(u_1,v_1\)を含む閉路ができてしまうからです。そうすると\(T^*\)が全域木であることに矛盾するので、\(T^*\)にない辺\((x_1,y_1)\)が必ず存在すると断言できます。
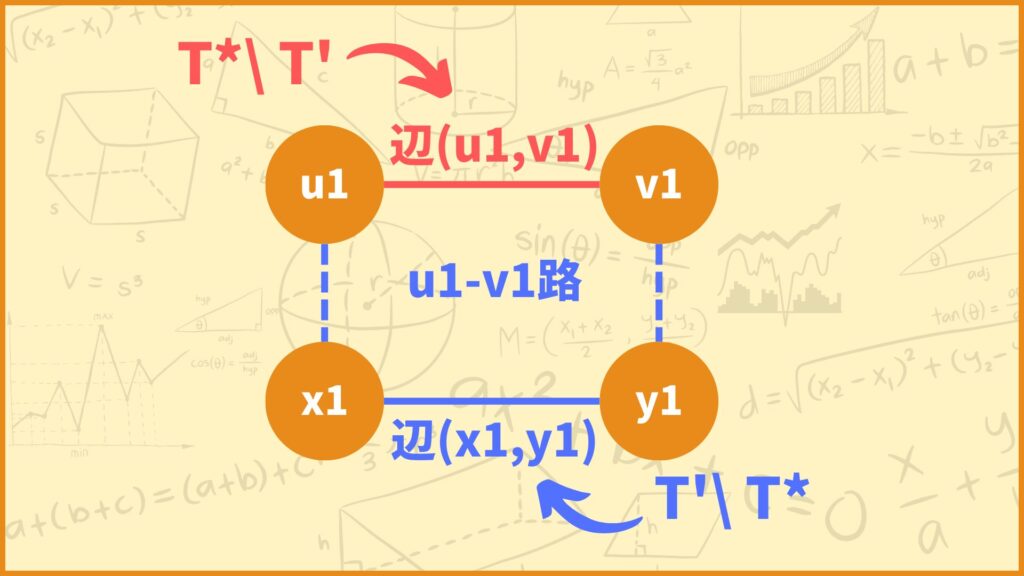
今条件Bが成り立つ辺が存在しないと仮定しているので、\(c(x_1,y_1) < c(u_1,v_1)\)となります。次に\(T^*\)中の\(x_1-y_1\)路について考えます。
(\(T^*\)は全域木なので、\(T^*\)中に\(x_1-y_1\)路が存在します。また\((x_1,y_1) \in T’ \backslash T^*\)なので\(T^*\)中に辺\((x_1,y_1)\)は存在しません。)
このとき、\(x_1-y_1\)路には\(T’\)中にない辺\((u_2,v_2)\)が存在します。
そのような辺\((u_2,v_2)\)が存在すると断言できるのもさっきと同じ理由で、もし存在しなければ\(u_2,v_2\)を含む閉路ができてしまい\(T’\)が全域木であることに矛盾するからです。
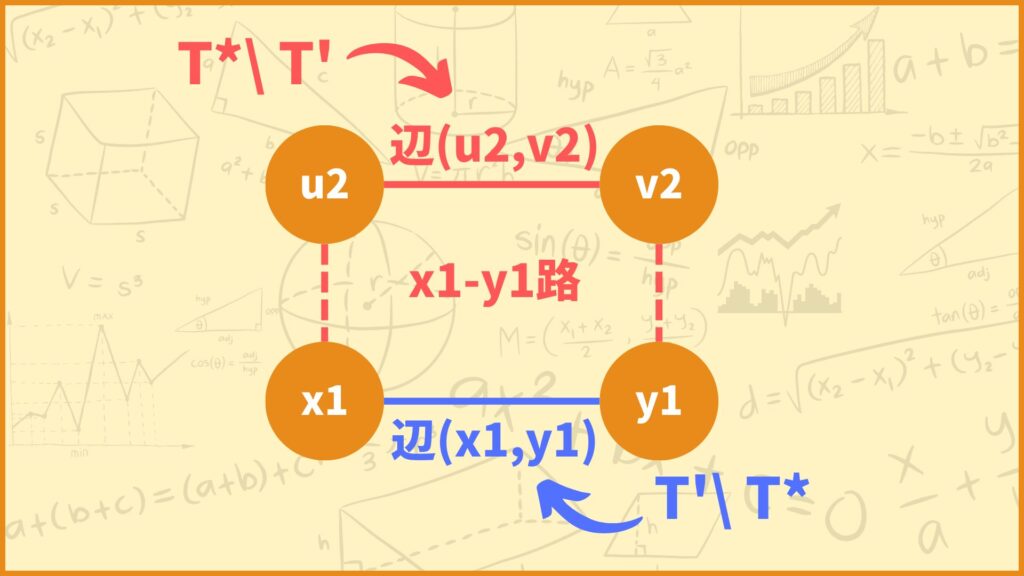
\(T^*\)は条件Aを満たす全域木なので、\(c(u_2,v_2) \leq c(x_1,y_1)\)となります。
この不等式とさっきの\(c(x_1,y_1) < c(u_1,v_1)\)を合わせると\(c(u_1,v_1)>c(u_2,v_2)\)が得られます。この議論を続けていくと\(c(u_1,v_1)>c(u_2,v_2)>c(u_3,v_3)>…\)という風に無限に続きます。
しかし\(T^*\)中の辺の数は有限なので、この不等式に矛盾します。ということで条件Bを満たす\(T^*\)中の辺\((u,v)\)が存在することが証明できました。
おわりに
いかがでしたか。
今回の記事ではクラスカル法について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
参考文献
Ding-Zhu Du, Panos M. Pardalos, Xiaodong Hu, Weili Wu, Introduction to Combinatorial Optimization. Springer, 2022, p.3-4



突然のコメント失礼します。
数式だけではなく、数式の表している状況が図示されており、大変分かりやすく感動しております。
ただ、必要条件の証明以降の部分で、誤植が含まれているようです。
そのためなのか頭の中でイメージが描けず、混乱しています。
(T、T’、T*等の表記に間違いはないでしょうか…?)
お忙しいなか申し訳ありません…。
時間がかかっても構いませんので、間違いがあれば修正していただけないでしょうか。
ぜひ前向きにご検討いただければと思います。よろしくお願いいたします。
ご指摘いただきありがとうございます。確認したところ、T*と表記するべき箇所をTと誤植しておりました。その他にも誤解を招くような記述がいくつかあったので修正いたしました。混乱を招いてしまい申し訳ございません。
早速の修正ありがとうございます!
本当にありがとうございました!!
こちらこそありがとうございます!