こんにちは!しゅんです!
今回の記事では動的計画法を使うのと使わないので実行時間がどれくらい変わるのかを検証してみました!
動的計画法はある問題の最適解を見つけるために使われる手法です。計算した値をメモして2回目以降はメモの値を利用することによって計算量を減らすという手法です。
では実際にどれくらい実行時間が短くなるのでしょうか。今回はpythonを使ってそれを検証したいと思います!
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
ナップサック問題を解く
今回はナップサック問題を解くプログラムを使って実行時間の比較をしたいと思います。
ナップサック問題を動的計画法で解く方法は以下の3つの記事で解説しています!
動的計画法じゃないver
動的計画法じゃなくて普通にナップサック問題を解くプログラムは以下のようになります。
## 動的計画法じゃなくて普通にナップサック問題を解く関数
def knapsack(cost, value, x):
if len(cost) == 0 or x < 1: # P(0,x), P(i,0)のとき
return 0,[] # 0と空リストを返す(空リストは最適解を返すときに使う)
elif cost[-1] > x: # 物iの重みがxより大きいとき
return knapsack(cost[:-1], value[:-1],x) # 物iは選ばないのでP(i-1,x)を返す
else: # 物iの重みがx以下のとき
ai = cost[-1] # 物iの重みにaiと名付ける
ci = value[-1] # 物iの満足度にciと名付ける
without_i, without_i_items = knapsack(cost[:-1],value[:-1],x) # 物iを選ばないとき:P(i-1,x)
with_i, with_i_items = knapsack(cost[:-1], value[:-1], x-ai) # 物iを選ぶとき:P(i-1,x-ai)
with_i += ci # 最適値にciを足す
if with_i > without_i: # iを選ぶときの方がiを選ばないときより満足度が大きい場合
return with_i, with_i_items+[len(cost) - 1] # P(i-1,x-ai)+ciを返す(with_i_itemsに物iのインデックスを追加)
else: # iを選ばないときの方がiを選ぶときより満足度が大きい場合
return without_i, without_i_items # P(i-1,x)を返す動的計画法ver
動的計画法でナップサック問題を解くプログラムは以下のようになります。
## ナップサック問題を解く関数
def knapsack2(cost, value, x, memo=None):
if memo is None: # メモを初期化する
memo = {}
if (len(cost), x) in memo: # メモがある場合はそれを返す
return memo[(len(cost), x)]
if len(cost) == 0 or x < 1: # P(0,x), P(i,0)のとき
return 0, [] # 0と空リストを返す(空リストは最適解を返すときに使う)
elif cost[-1] > x: # 物iの重みがxより大きいとき
result = knapsack2(cost[:-1], value[:-1], x, memo) # 物iは選ばないのでP(i-1,x)をresultに格納
memo[(len(cost), x)] = result # メモ化
return memo[(len(cost),x)] # メモを返す
else: # 物iの重みがx以下のとき
ai = cost[-1] # 物iの重みにaiと名付ける
ci = value[-1] # 物iの満足度にciと名付ける
without_i, without_i_items = knapsack2(cost[:-1], value[:-1], x, memo) # 物iを選ばないとき:P(i-1,x)
with_i, with_i_items = knapsack2(cost[:-1], value[:-1], x - ai, memo) # 物iを選ぶとき:P(i-1,x-ai)
with_i += ci # 最適値にciを足す
if with_i > without_i: # iを選ぶときの方がiを選ばないときより満足度が大きい場合
result = with_i, with_i_items + [len(cost) - 1] # P(i-1,x-ai)+ciをresultに格納(with_i_itemsに物iのインデックスを追加)
else: # iを選ばないときの方がiを選ぶときより満足度が大きい場合
result = without_i, without_i_items # P(i-1,x)をresultに格納
memo[(len(cost), x)] = result # メモ化
return memo[len(cost),x]
基本はさっきのやつと一緒ですが、辞書をメモとして活用して動的計画法を実装しています。
実行時間を調べる
選択肢の数が増えると実行時間も大きくなると考えられるので、選択肢が5個、10個、15個、20個、25個、30個、35個それぞれの場合に対して実行時間がどう変化するかを見てみましょう。
今回の検証では重みが1~8の間の整数、満足度は10~90の間の整数の中からランダムに抽出します。
動的計画法じゃないver
以下のコードでプログラムの実行時間を計測できます。
import time # timeをインポートする
import random # randomをインポートする
random.seed(1) # ランダム値を固定
# コードの実行開始時刻を記録
start_time = time.time()
num = [5,10,15,20,25,30,35] # 要素数のリストを作成
result = [] # 結果を格納する空リストを作成
for n in num:
# ナップサック問題のプログラムを実行
C = [random.randint(1,8) for i in range(n)] # 重みをランダムにn個生成
V = [random.randint(10,90) for i in range(n)] #満足度をランダムにn個生成
X = n # 重量制限をnに設定
knapsack(C,V,X) # ナップサック問題を解く
# コードの実行終了時刻を記録
end_time = time.time()
# 実行時間を計算して表示
execution_time = end_time - start_time # 実行時間の計算
result.append(execution_time) # 結果をresultに格納
print(f"実行時間(選択肢:{n}個):", execution_time, "秒") # 実行時間の表示
今回はプログラムがメインではないので説明は簡単にします。実行時間はtimeモジュールを使えば計測できます。randomをインポートすることで重みと満足度をランダム設定できます。
選択肢の個数\(n=5,10,…,35\)それぞれに対して、ナップサック問題を実行して実行時間を記録して表示しています。
これを見ると選択肢が5個~25個のときは一瞬で終わっていますが選択肢が30個になると約8秒かかり、35個になると一気に約74秒まで跳ね上がっていますね。選択肢が35個以上になると時間がかかりすぎてあまり使い物にならなさそうですね。
ちなみに選択肢が40個でこのコードを実行したら5分くらい経っても計算が終わりませんでした。
動的計画法ver
それでは次に動的計画法verで実行時間を測ってみましょう。先ほどのコードのknapsackをknapsack2にすればOKです。
import time # timeをインポートする
import random # randomをインポートする
random.seed(1) # ランダム値を固定
# コードの実行開始時刻を記録
start_time = time.time()
num = [5,10,15,20,25,30,35] # 要素数のリストを作成
result2 = [] # 結果を格納する空リストを作成
for n in num:
# ナップサック問題のプログラムを実行
C = [random.randint(1,8) for i in range(n)] # 重みをランダムにn個生成
V = [random.randint(10,90) for i in range(n)] #満足度をランダムにn個生成
X = n # 重量制限をnに設定
knapsack2(C,V,X) # ナップサック問題を解く
# コードの実行終了時刻を記録
end_time = time.time()
# 実行時間を計算して表示
execution_time = end_time - start_time # 実行時間の計算
result2.append(execution_time) # 結果をresultに格納
print(f"実行時間(選択肢:{n}個):", execution_time, "秒") # 実行時間の表示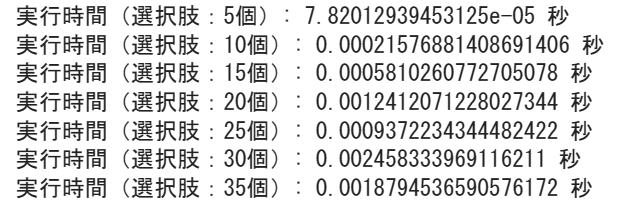
ということで動的計画法verのプログラムの実行時間を求めることができました。こちらは選択肢が30個、35個になってもあまり実行時間が増えていないですね。
ちなみにこっちのverだと選択肢を40,45,…と増やしてもすぐ実行できました。ということで選択肢を500個、600個、700個、800個、900個に増やしたところ、以下のような結果になりました。

さすがに900個とかになると結構時間がかかっちゃいますね。
実行時間を比較する
それでは最後に2つのコードの実行時間を比較してみましょう。明らかに動的計画法を使った方が実行時間が短いことが分かりますね。

特に選択肢の個数が大きくなるにつれてその差は顕著に現れます。グラフにしてみると非常にわかりやすいと思います。
import matplotlib.pyplot as plt
plt.plot(num, result, marker = "o", color = "blue", alpha = 0.5, markersize = 10, label = "non-dp")
plt.plot(num, result2, marker = "o", color = "green", alpha = 0.5, markersize = 10, label = "dp")
plt.yscale("log")
plt.xlabel("Number of elements")
plt.ylabel("Execution time (log scale)")
plt.title("Comparison of execution time")
plt.legend()
plt.show()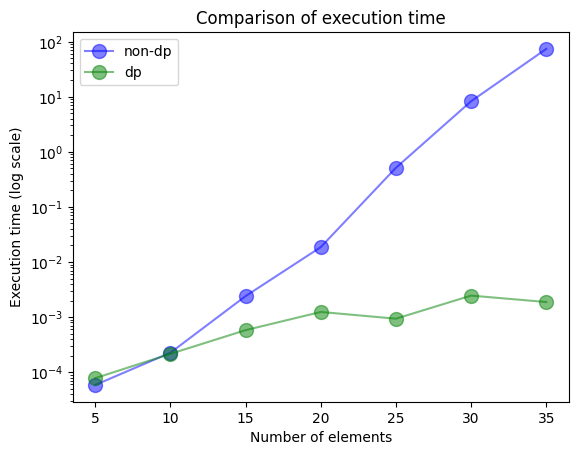
pythonのmatplotlibを使って折れ線グラフ作成しました。横軸が選択肢の個数、縦軸が実行時間です。分かりやすいように片対数グラフにしてみました。青線が動的計画法じゃないverで、緑線が動的計画法verです。
このグラフを見ると違いが一目瞭然ですね。要素数が35程度でこんなに差が開いているので、要素数を増やすともっと差が開くことが想像できます。
このように動的計画法を使うのと使わないのでは全然計算量が違います。
※青線は比例しているっぽいですね。片対数グラフで比例するということは、指数乗に比例するということです。つまり動的計画法を使わないverは指数時間のアルゴリズムだと予測できますね。
動的計画法じゃないverと動的計画法verの計算量についてはこちらの記事で説明しています!
現在制作中
おわりに
いかがでしたか。
今回の記事では動的計画法について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。