こんにちは!しゅんです!
今回の記事では同値関係について解説していきます!
数学では「等しい」や「同じ」という物事を同値と表すことがあります。この同値関係っていったいどのような状態なのでしょうか。
この記事では同値関係がどんなものなのかについて解説していきます!
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
高校数学でまでで登場する同値関係の例

数学で登場する「等しい」や「同じ」を表す数学用語は\(=\)(イコール)だと思います。
\(x\)と\(y\)が同じ値のとき\(x=y\)と表します。これは一番理解しやすい同値の例だと思います。
他にも、高校数学で登場する\(\equiv\)(合同式)も「等しい」、「同じ」を表す記号です。より詳細に言うと、\(x \equiv y \pmod k\)とは\(x\)を\(k\)で割った時の余りと\(y\)を\(k\)で割った時の余りが等しいことを表します。
例えば\(x=1, y=4\)のとき、\(x,y\)を3で割った余りはどちらも1です。このとき\(1 \equiv 4 \pmod 3\)という風に表します。
これも余りが3の世界では1と4は等しいということを表しています。
同値関係ってなに?
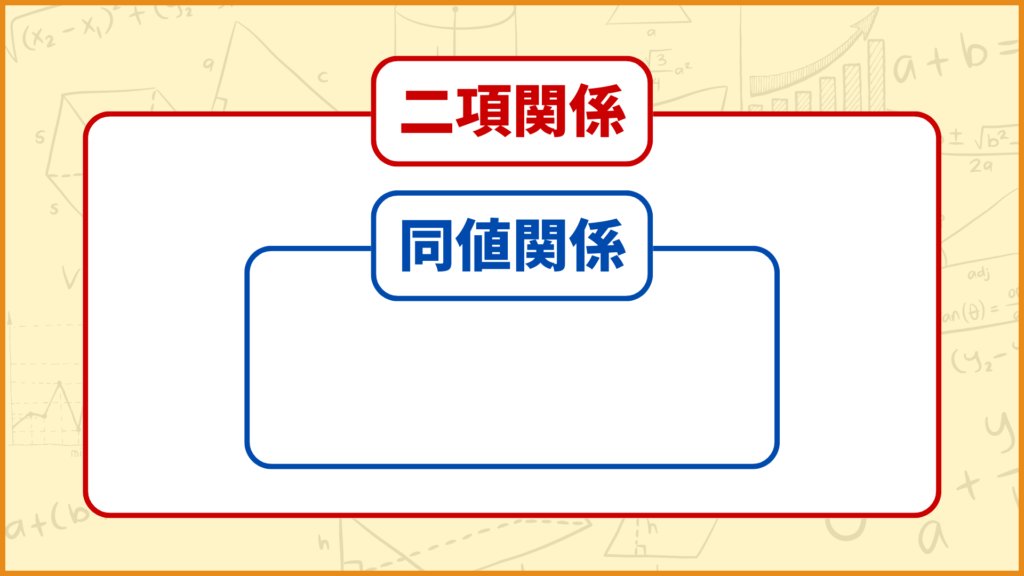
結論同値関係は以下の条件を満たすものです。
集合\(X\)上の2項関係\(R\)のうち以下の条件を満たすもの。
1 : 任意の\(x \in X\)について\((x,x) \in R\)が成立
2 : 任意の\(x,y \in X\)について\((x,y) \in R\)ならば\((y,x) \in R\)が成立
3 : 任意の\(x,y,z \in X\)について\((x,y) \in R, \; (y,z) \in R\)ならば\((x,z) \in R\)が成立
これだけ見ても何が何だか分からないので1つずつ噛み砕いてなるべく分かりやすく説明していきます。
2項関係ってなに?
まず2項関係とは、ある集合の中から2つ要素を取ってきてペアにしたものをいくつか集めた集合です。
例えばある集合が\(X=\{1,2,3,4,5\}\)だとします。ここから適当に2つ要素を取ってきます。

上の図では(1,1), (1,4), (2,5), (3,3), (3,5), (4,5)を取ってきています。これらのペアたちをまとめて集合にしたものが2項関係です。上の例だと2項関係\(R\)は
\(R = \{(1,1), (1,4), (2,5), (3,3), (3,5), (4,5)\}\)
となります。これが2項関係です。この2項関係の中でもさっき挙げた3つの条件を満たすものが同値関係という風になります。
1つ目の条件(反射律)ってなに?
次に1つ目の条件について解説したいと思います。1つ目の条件は反射律と呼ばれます。
任意の\(x \in X\)について\((x,x) \in R\)が成立
例えば\(X=\{1,2,3,4,5\}\)だったら\(R\)には(1,1), (2,2), (3,3), (4,4), (5,5)が入ってないといけないってことです。

上の図で言うと2項関係\(R_1\)には(1,1), (2,2), (3,3), (4,4), (5,5)が入っているので反射律を満たします。一方\(R_2\)には(2,2)と(4,4)がないので反射律を満たしません。
2つ目の条件(対称律)ってなに?
次に2つ目の条件について解説したいと思います。2つ目の条件は対称律と呼ばれます。
任意の\(x,y \in X\)について\((x,y) \in R\)ならば\((y,x) \in R\)が成立

例えば2項関係\(R\)に(1,2)が入っているとします。このとき対称律を満たすためには\(R\)に(2,1)が入っている必要があります。
上の図で言うと2項関係\(R_1\)は対称律を満たします。一方\(R_2\)には(3,4)があるのに(4,3)がないので対称律を満たしません。
3つ目の条件(推移律)ってなに?
最後に3つ目の条件について解説したいと思います。3つ目の条件は推移律と呼ばれます。
任意の\(x,y,z \in X\)について\((x,y) \in R, \; (y,z) \in R\)ならば\((x,z) \in R\)が成立

例えば2項関係\(R\)に(1,2)と(2,3)が入っているとします。このとき推移律を満たすためには\(R\)に(1,3)が入っている必要があります。
上の図で言うと\(R_1\)は推移律を満たします。一方\(R_2\)には(1,2), (2,4)が入っているのに(1,4)が入っていないので推移律を満たしません。
反射律・対称律・推移律を満たす2項関係が同値関係
以上の3つの条件を満たす2項関係\(R\)のことを同値関係と言います。たとえば\(X=\{1,2,3,4,5\}\)としたときの同値関係の例を見てみましょう。
まず反射律を満たさないといけないので、\(R\)には(1,1), (2,2), (3,3), (4,4), (5,5)が入っている必要があります。
\(R = \{(1,1),(2,2),(3,3),(4,4),(5,5)\}\)
次に対称律を満たすようにします。例えば(1,4)と(4,5)が入っているとします。このとき対称律を満たすためには(4,1)と(5,4)が入っている必要があります。
\(R = \{(1,1),(2,2),(3,3),(4,4),(5,5),\)
\((1,4),(4,5),(4,1),(5,4)\}\)
最後に推移律を満たすようにします。\(R\)には(1,4)と(4,5)が入っているので、推移律を満たすためには(1,5)が入っている必要があります。また(5,4)と(4,1)が入っているので(5,1)が入っている必要があります。
\(R = \{(1,1),(2,2),(3,3),(4,4),(5,5),\)
\((1,4),(4,5),(4,1),(5,4),(1,5),(5,1)\}\)
上の\(R\)が同値関係の具体例となります。
同値関係の例
等号(=)
最初に説明したように、等号は同値関係になります。整数集合\(\mathbb{Z}\)上の2項関係\(R\)を
\(R=\{(x,y) \in \mathbb{Z} \times \mathbb{Z} \; | \; x=y\}\)
と定義します。この2項関係\(R\)は反射律・対称律・推移律をすべて満たすので同値関係となります。
反射律:
任意の\(x \in \mathbb{Z}\)に対して\(x=x\)なので(当たり前)\((x,x) \in R\)となります。
対称律:
任意の\(x,y \in \mathbb{Z}\)に対して\(x=y\)のとき\(y=x\)なので(当たり前)\((x,y) \in R\)ならば\((y,x) \in R\)となります。
推移律:
任意の\(x,y,z \in \mathbb{Z}\)に対して\(x=y, \; y=z\)ならば\(x=z\)なので(当たり前)\((x,y) \in R, \; (y,z) \in R\)ならば\((x,z) \in R\)となります。
合同式(≡)
合同式も最初に説明したように同値関係になります。集合\(\mathbb{Z}\)上の2項関係\(R\)を
\(R=\{(x,y) \in \mathbb{Z} \times \mathbb{Z} \; | \; x \equiv y \pmod k\}\)
\(k\)は2以上の自然数
と定義します。この2項関係\(R\)は反射律・対称律・推移律をすべて満たすので同値関係となります。
反射律:
任意の\(x \in \mathbb{Z}\)に対して\(x\equiv x \pmod k\)なので(当たり前)\((x,x) \in R\)となります。
対称律:
任意の\(x,y \in \mathbb{Z}\)に対して\(x \equiv y \pmod k\)のとき\(y \equiv x \pmod k\)なので\((x,y) \in R\)ならば\((y,x) \in R\)となります。
例)\(4 \equiv 1 \pmod 3\)のとき\(1 \equiv 4 \pmod 3\)
推移律:
任意の\(x,y,z \in \mathbb{Z}\)に対して\(x\equiv y \pmod k, \; y\equiv z \pmod k\)ならば\(x \equiv z \pmod k\)なので\((x,y) \in R, \; (y,z) \in R\)ならば\((x,z) \in R\)となります。
例)\(4 \equiv 1 \pmod 3, \; 1 \equiv 7 \pmod 3\)のとき\(4 \equiv 7 \pmod 3\)
イメージ的には\(k\)で割ったあまりが同じ数字は\(\text{mod} \; k\)の世界では同じって感じです。
無向グラフのパス
無向グラフのパスも同値関係となります。無向グラフ\(G=(V,E)\)に対して2項関係\(R\)を
\(R= \{(v,w) \in V \times V \; | \; G \text{に}v-w\text{路が存在する}\}\)
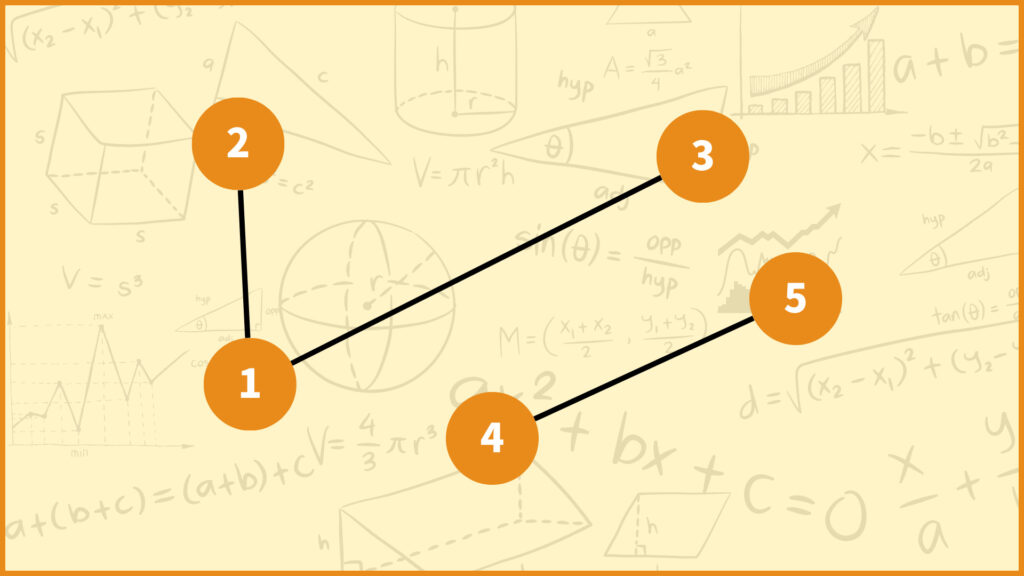
例えば上の無向グラフに対する\(R\)は
\(R = \{(1,1),(2,2),(3,3),(4,4),(5,5),\)
\((1,2),(2,1),(1,3),(3,1),(2,3),(3,2),(4,5),(5,4)\}\)
となります。この\(R\)は同値関係となります。(自分自身へは長さ0のパスが存在すると考えてください。)
反射律:
任意の\(v \in V\)に対して\(v-v\)路が存在するので\((v,v) \in R\)となります。
対称律:
任意の\(v,w \in V\)に対して\(v-w\)路が存在するとき\(w-v\)路が存在するので(無向グラフだから)\((v.w) \in R\)ならば\((w,v) \in R\)となります。
推移律:
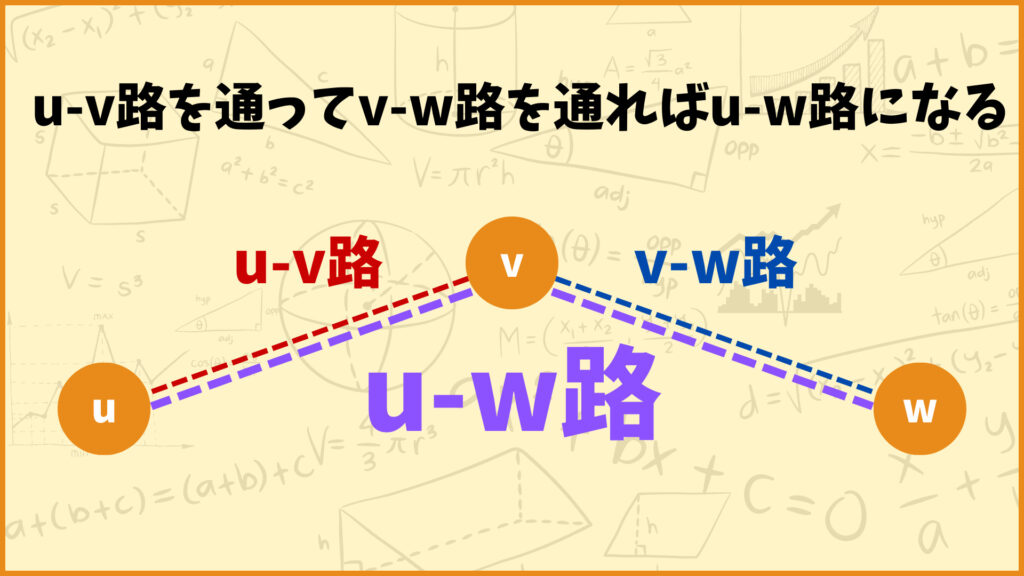
任意の\(u,v,w \in V\)に対して\(u-v\)路と\(v-w\)路が存在するとき\(u-w\)路が存在するので(下図参照)\((u,v) \in R, \; (v,w) \in R\)ならば\((u,w) \in R\)となります。
イメージ的には間にパスが存在する頂点同士は同じ種類の頂点って感じです。
おわりに
いかがでしたか。
今回の記事では同値関係について解説していきました。
今後もこのような離散数学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。




