半順序集合を分かりやすく表した有向グラフ
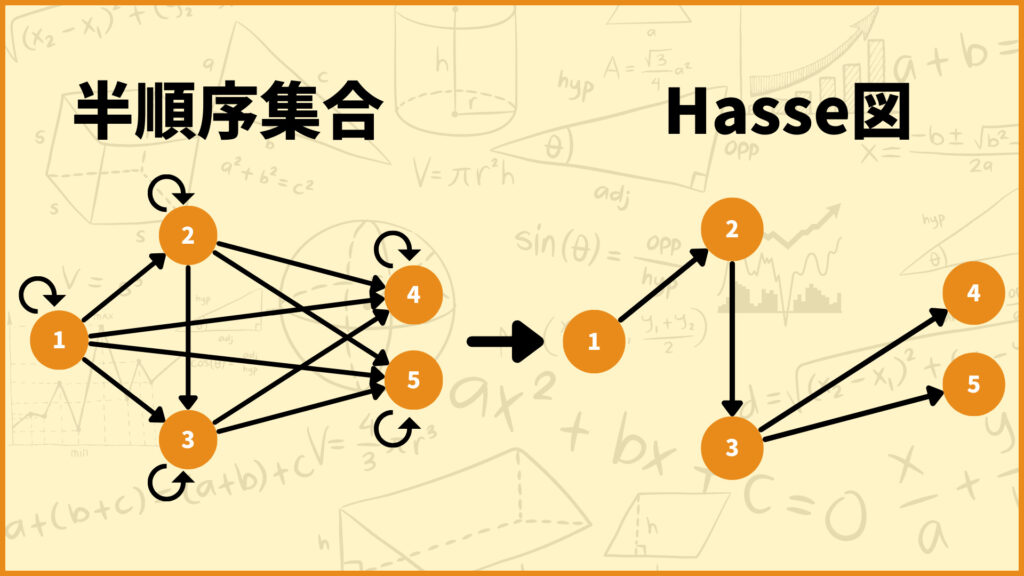
半順序集合\((X,R)\)は集合\(X\)を頂点集合、半順序\(R\)を有向辺の集合と考えることで有向グラフを描くことができます。
半順序・半順序集合はこちらの記事で解説しています!
例えば上の図の左側のグラフは以下の半順序集合\((X,R)\)を有向グラフで表したものです。
\(X=\{1,2,3,4,5\}\)
\(R=\{(1,1),(2,2),(3,3),(4,4),(5,5),\)
\((1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5)\}\)
だけどこのグラフ結構ごちゃごちゃしていますよね。もっと見やすく、かつ必要な情報が省略されていないグラフを作りたいです。ということで出来たグラフが右側のHasse図です。
Hasse(ハッセ)図のちゃんとした定義
ということで次はHasse図のちゃんとした定義を説明したいと思います。めっちゃ数学用語が出てくるので、もし難しければ先に「Hasse(ハッセ)図の作り方の例」の所を見てみてください。
集合\(X\)上の半順序\(R\)に対して以下の2項関係\(R’,R_H\)を考える。
\(R’=R \; \backslash \; \{(x,x) \; | \; x \in X\}\)
\(R_H = \{(x,y) \in R’ \; | \; (x,z), (z,y) \in R’ \text{となる} z \text{が存在しない}\}\)
このとき\((X,R_H)\)を半順序集合\((X,R)\)に対するHasse図という。
いきなり\(R’\)とか\(R_H\)とか出てきてもよく分からないですよね。ということでこの2つの説明をしていきます。
\(R’\)ってなに?
\(R’=R \; \backslash \; \{(x,x) \; | \; x \in X\}\)
\(R’\)の定義式を見てみましょう。\(R’\)は半順序\(R\)から\(\{(x,x) \; | \; x \in X\}\)を除いたものです。例えば\(X=\{1,2,3,4,5\}\)だとすると、
\(\{(x,x) \; | \; x \in X\}\)は\((1,1),(2,2),(3,3),(4,4),(5,5)\)となります。
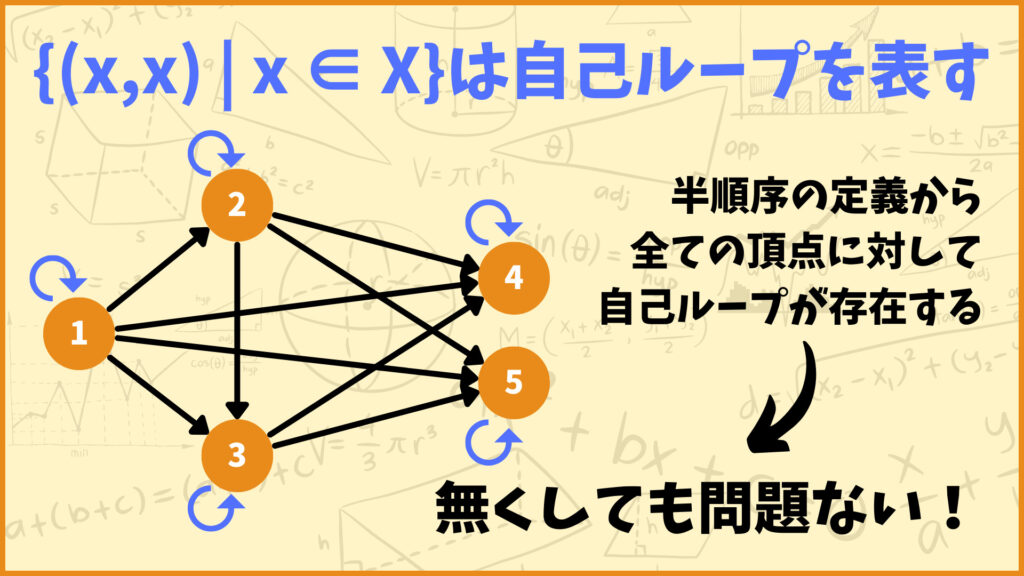
つまり\(\{(x,x) \; | \; x \in X\}\)は半順序集合\((X,R)\)を有向グラフにしたときの自己ループの集合と対応します。半順序は反射律を満たすので任意の頂点に対して自己ループが存在します。よってこれらの自己ループは除去しても問題なさそうです。
\(R’\)は元々のグラフの有向辺から自己ループを取り除いたものの集合
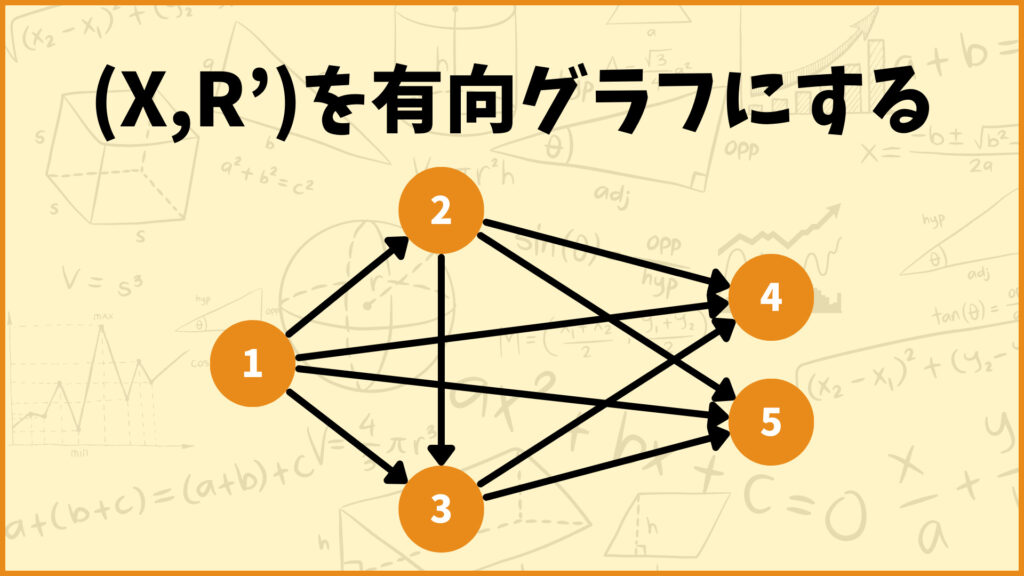
\(R_H\)ってなに?
\(R_H = \{(x,y) \in R’ \; | \; (x,z), (z,y) \in R’ \text{となる} z \text{が存在しない}\}\)
\(R_H\)の定義式を見てみます。\(R_H\)の要素\((x,y)\)は\(R’\)に属すモノの中で、\((x,z),(z,y) \in R’\)となる\(z\)が存在しないモノです。
さっきのグラフを使って具体的にを考えてみましょう。
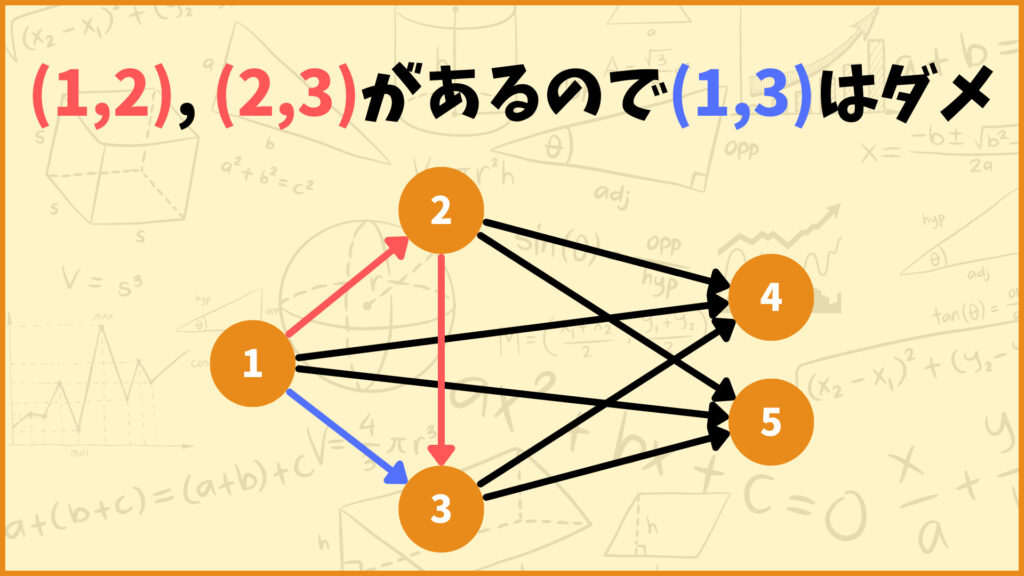
例えば上の図を見ると分かるように、\((1,2),(2,3) \in R’\)なので\((1,3)\)は\(R_H\)の要素ではありません。他にも\((1,2),(1,4) \in R’\)なので\((1,4)\)は\(R_H\)の要素ではありません。
このように考えると、\(R_H\)を作るために\(R’\)から取り除く必要がある要素は
\((1,3),(1,4),(1,5),(2,4),(2,5)\)です。これらを取り除くと以下のような有向グラフが得られます。
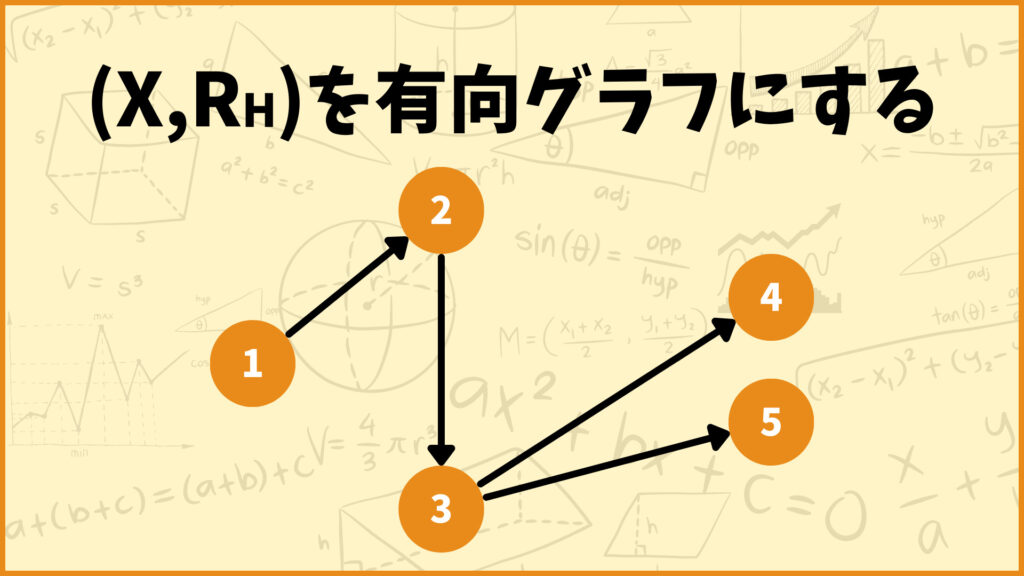
このようにして得られた有向グラフのことをHasse図と言います。Hasse図を見るだけでどの要素間に関係があるのかが分かります。
例えば頂点1から頂点3へと向かうパスが存在するので、\((1,3) \in R\)であることが分かります。他にも頂点2から頂点5へと向かうパスが存在するので、\((2,5) \in R\)であることが分かります。
Hasse(ハッセ)図の作り方の例
以下の3つの半順序についてHasse図を描いていこうと思います。
(\(R_1\)は集合\(X_1=\{1,2,3,4\}\)上の半順序、\(R_2\)は集合\(X_2=\{1,2,3,4,5\}\)上の半順序、\(R_3\)は集合\(X_3=\{1,2,3,4,5,6\}\)上の半順序です。)

具体例.1
\(R_1 = \{(1,1),(2,2),(3,3),(4,4),\)
\((1,2),(2,3),(1,3),(4,2),(4,3)\}\)
半順序集合\((X_1,R_1)\)を有向グラフで表すと以下のようになります。
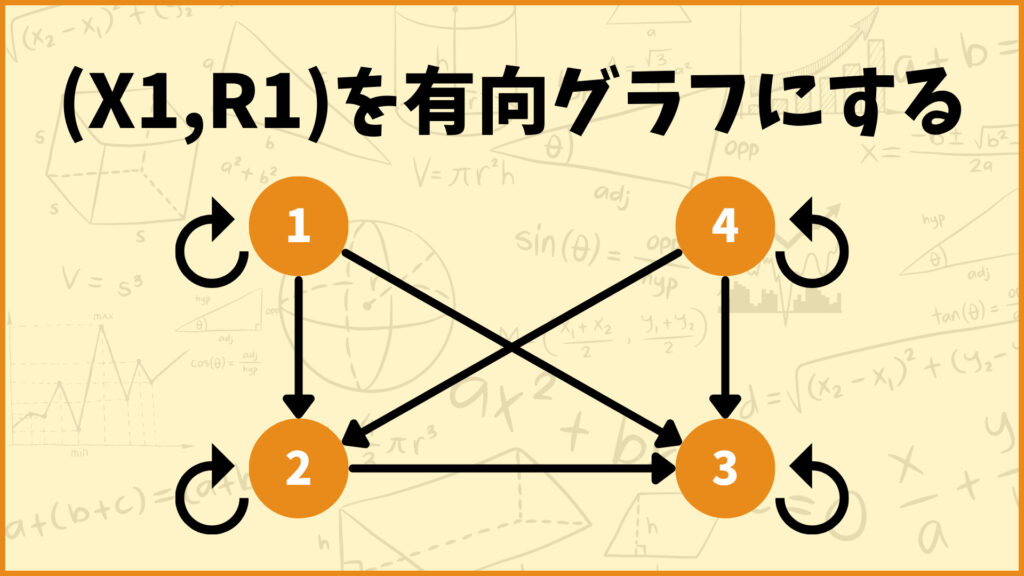
まずは4つの自己ループを取り除きましょう。\(R_1\)から自己ループを取り除いた集合は\(\{(1,2),(2,3),(1,3),(4,2),(4,3)\}\)となります。
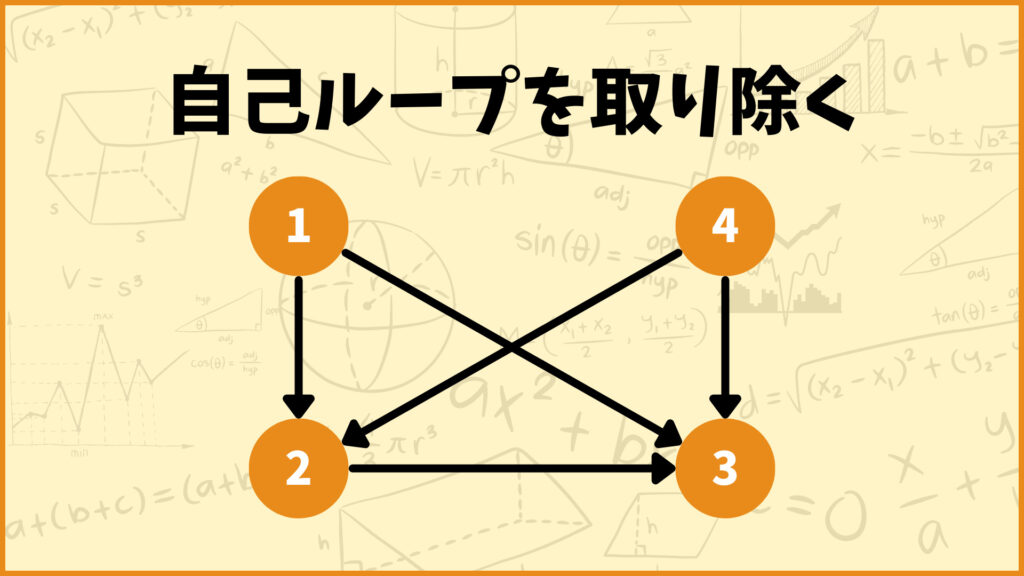
次に、そこを使わなくても回り道して到達できるような辺を探します。例えば頂点1から頂点3の間のパスを考えてみましょう。2つの頂点を直接結ぶ辺\((1,3)\)を使わなくても、辺\((1,2),(2,3)\)を使えば頂点\(1 \to 2 \to 3\)の順番で到達できます。この場合辺\((1,3)\)は必要ないので削除します。
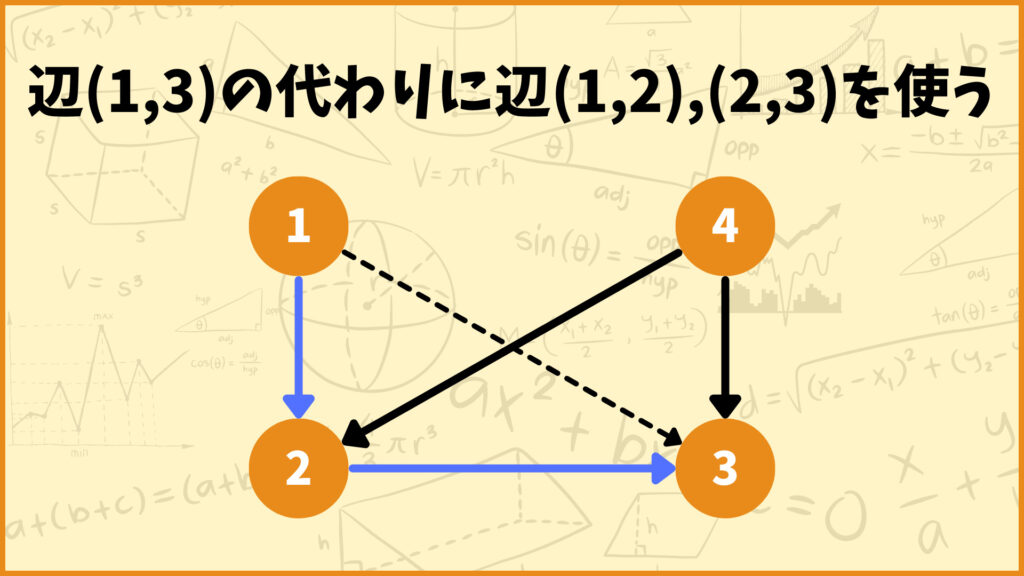
同じように考えると、辺\((4,2)\)の代わりに辺\((4,3),(3,2)\)を使えば頂点4から頂点2に到達できるので、辺\((4,2)\)は削除します。最終的に残った辺の集合は\(R_H=\{(1,2),(2,3),(4,3)\}\)となります。
このようにして作成されたグラフが\((X_1,R_1)\)に対するHasse図です。
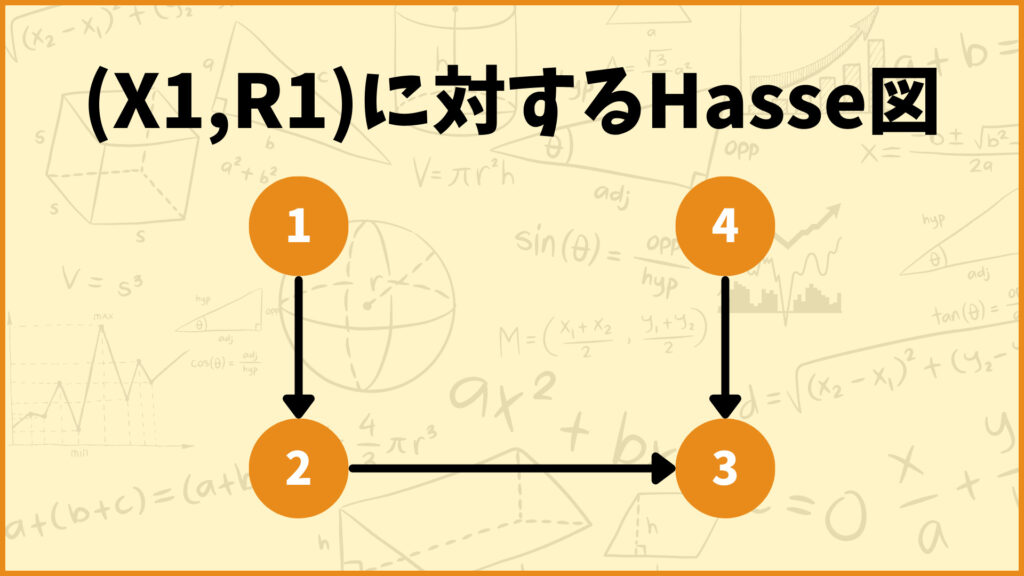
具体例.2
\(R_2 = \{(1,1),(2,2),(3,3),(4,4),(5,5),\)
\((5,1),(1,4),(5,4),(4,3),(5,3),(1,3)\}\)
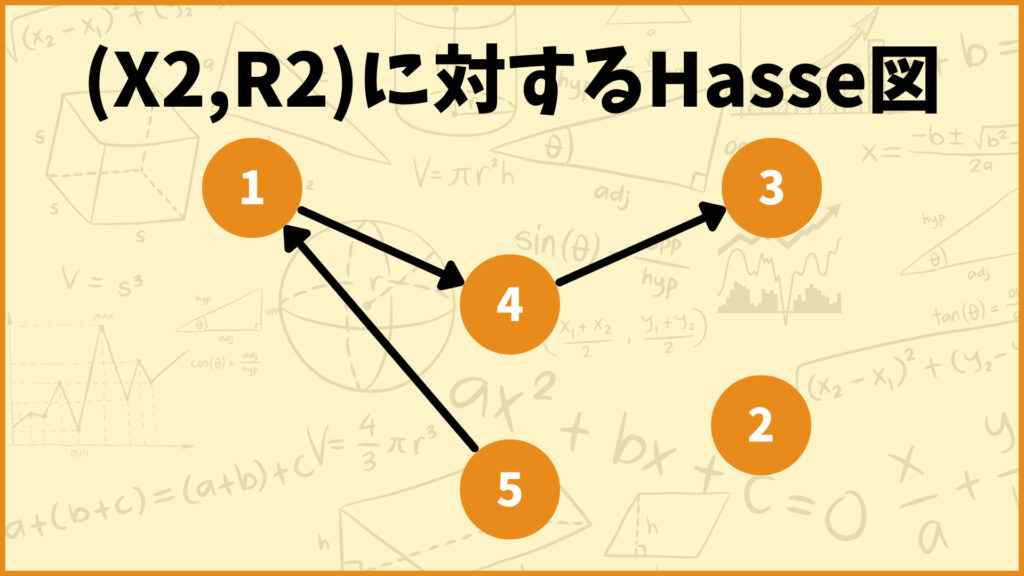
半順序集合\((X_2,R_2)\)を有向グラフで表すと以下のようになります。
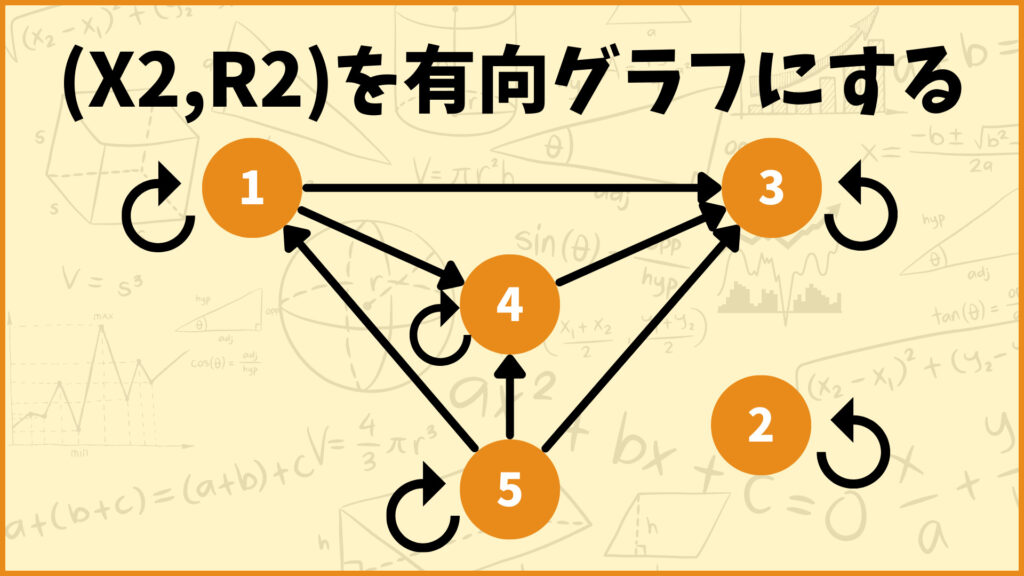
これも具体例1と同じようにやっていきます。まず最初に自己ループ\((1,1),(2,2),(3,3),(4,4),(5,5)\)を取り除きます。この時点で残った辺の集合は\(\{(5,1),(1,4),(5,4),(4,3),(5,3),(1,3)\}\)です。
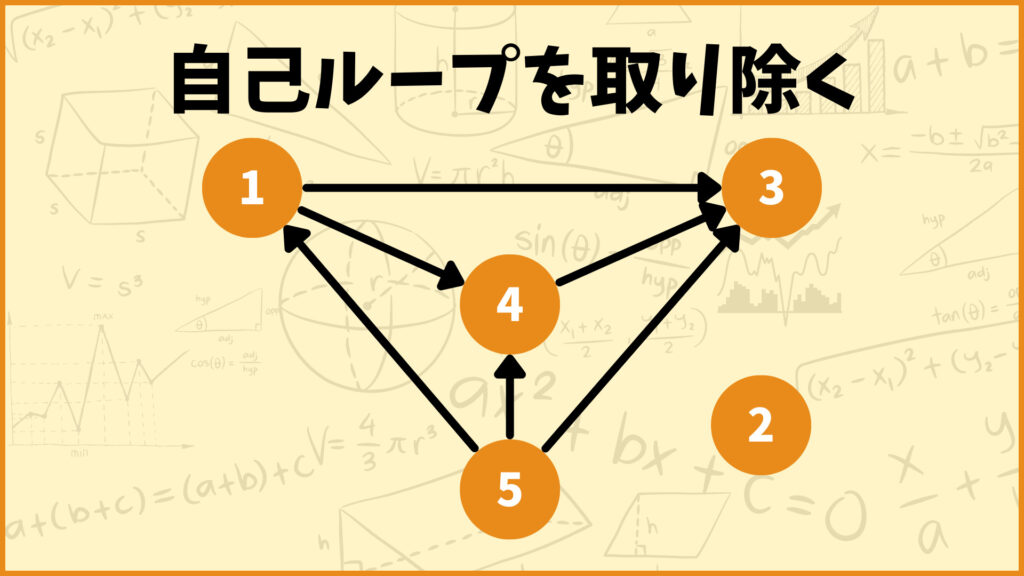
次に回り道できるところを探して取り除きます。今回の場合は辺\((5,4)\)と辺\((5,3)\)と辺\((1,3)\)を取り除きます。
辺\((5,4)\)の代わりに辺\((5,1),(1,4)\)をたどれば頂点5から頂点1にたどり着けます。
辺\((5,3)\)の代わりに辺\((5,4),(4,3)\)をたどれば頂点5から頂点3にたどり着けます。
辺\((1,3)\)の代わりに辺\((1,4),(4,3)\)をたどれば頂点1から頂点3にたどり着けます。
これらの辺をすべて取り除いた結果残った辺の集合は\(\{(5,1),(1,4),(4,3)\}\)となります。
このようにして作成されたグラフが\((X_2,R_2)\)に対するHasse図です。
具体例.3
\(R_3 = \{(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)\)
\((3,6),(6,2),(3,2),(2,5),(3,5),(5,1),(3,1)\}\)
半順序集合\((X_3,R_3)\)を有向グラフで表すと以下のようになります。
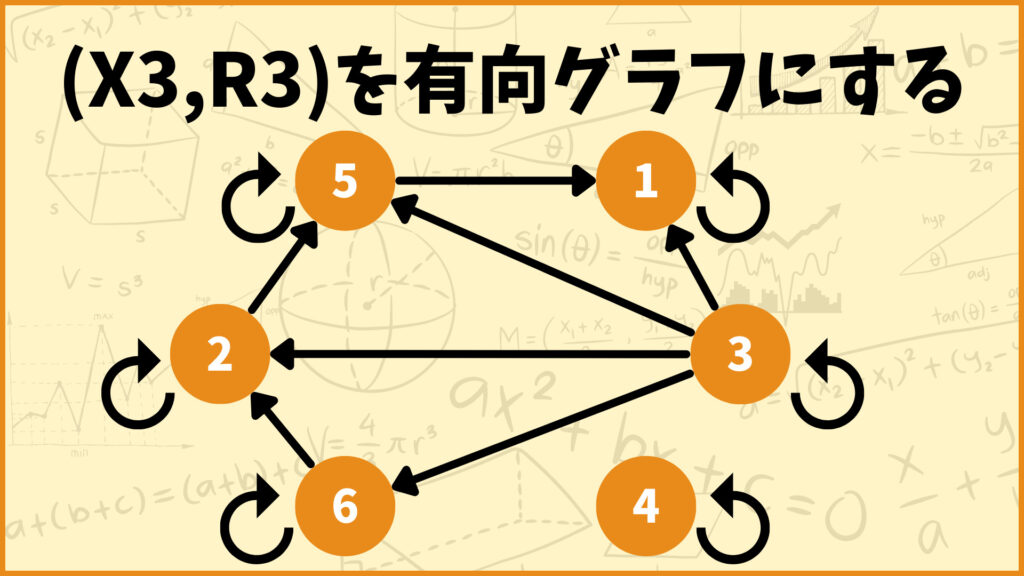
これも具体例1と同じようにやっていきます。まず最初に自己ループ\((1,1),(2,2),(3,3),(4,4),(5,5),(6,6)\)を取り除きます。この時点で残った辺の集合は\(\{(3,6),(6,2),(3,2),(2,5),(3,5),(5,1),(3,1)\}\)です。
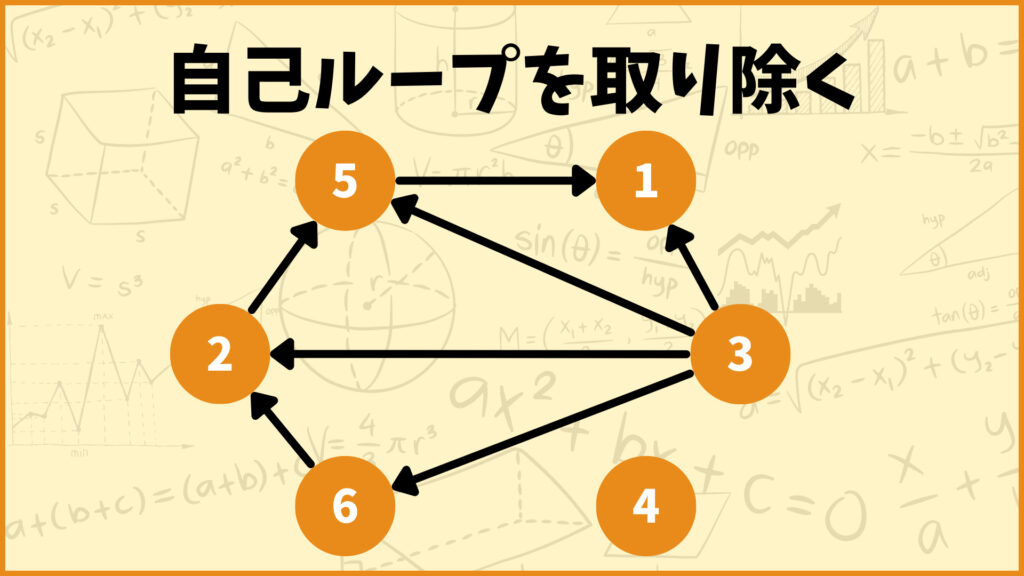
次に回り道できるところを探して取り除きます。今回の場合は辺\((3,2)\)と辺\((3,5)\)と辺\((3,1)\)を取り除きます。
辺\((3,2)\)の代わりに辺\((3,6),(6,2)\)をたどれば頂点3から頂点2にたどり着けます。
辺\((3,5)\)の代わりに辺\((3,2),(2,5)\)をたどれば頂点3から頂点5にたどり着けます。
辺\((3,1)\)の代わりに辺\((3,5),(5,1)\)をたどれば頂点3から頂点1にたどり着けます。
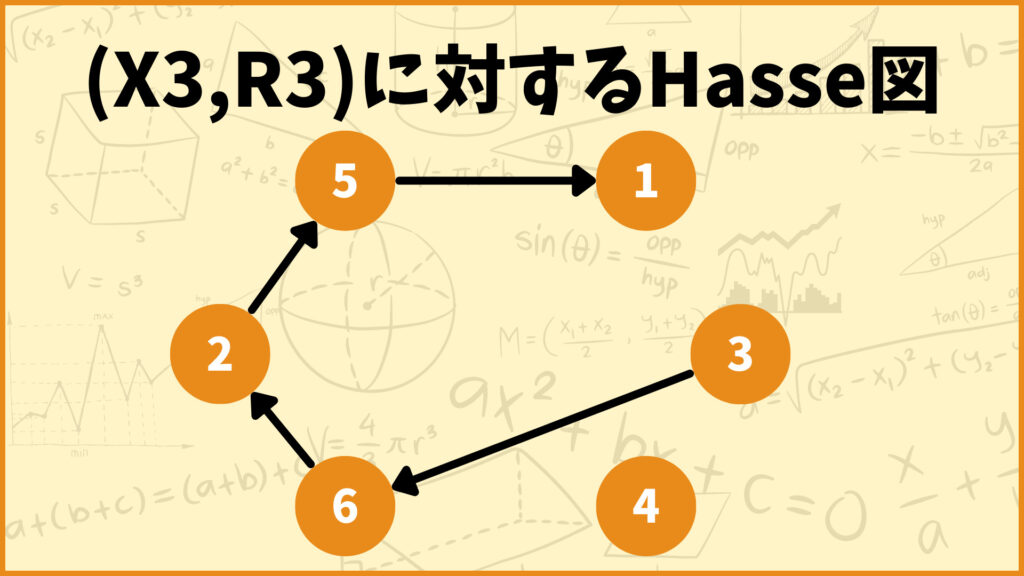
これらの辺をすべて取り除いた結果残った辺の集合は\(\{(3,6),(6,2),(2,5),(5,1)\}\)となります。
このようにして作成されたグラフが\((X_3,R_3)\)に対するHasse図です。
おわりに
いかがでしたか。
今回の記事ではHasse図について解説していきました。
今後もこのような離散数学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。