こんにちは!しゅんです!
いきなりですが中学の数学で2次関数を勉強すると下のような問題に出くわしますよね。
関数\(y=3x^2\)について、\(x\)の値が-1から3まで増加するときの変化の割合を求めなさい。
関数\(y=ax^2\)と\(y=3x+4\)について、\(x\)の値が2から4まで増加するときの変化の割合が等しくなる。このとき\(a\)の値を求めなさい。
この問題を解くために謎の公式を使って解いたりします。
謎の公式:
\(y=ax^2\)において\(x\)の値が\(x_1\)から\(x_2\)まで増加するときの変化の割合は
\(a(x_1+x_2)\)
で表せる。
この公式って何なんでしょうか。そしてそもそも2次関数の変化の割合って何を表しているのでしょうか。この記事ではこれらについて図を使って説明したいと思います!
1次関数の変化の割合
2次関数の変化の割合を理解するためにはまず最初に1次関数の変化の割合を知っておく必要があります。
1次関数の変化の割合は直線の傾きだということが分かっている人はこの章を飛ばして大丈夫です。
変化の割合の公式
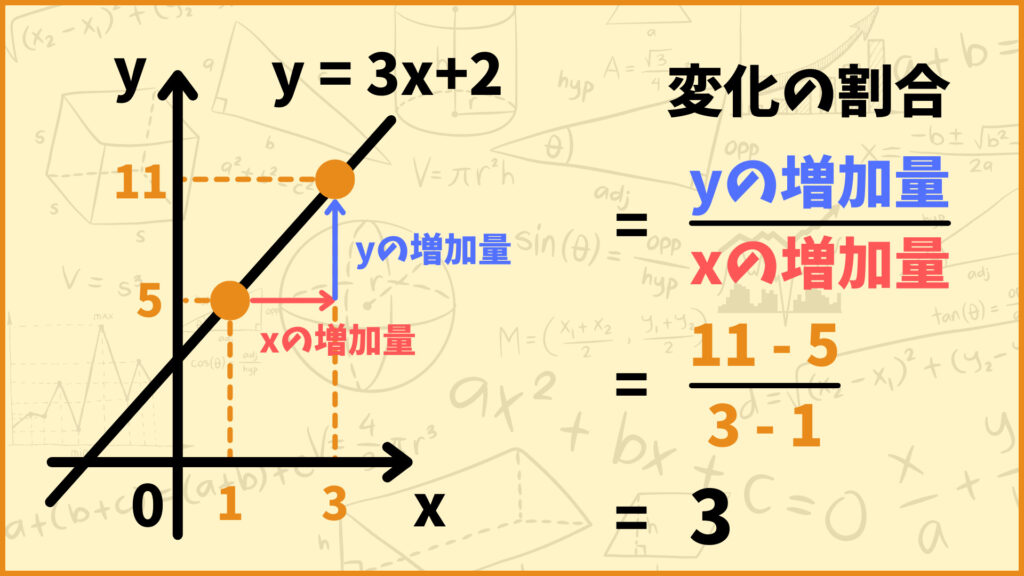
変化の割合の公式は
変化の割合 = yの増加量 / xの増加量
です。例えば上のグラフ\(y=3x+5\)の変化の割合について考えてみましょう。\(x\)が1から3まで増加するとき、\(y\)は5から11まで増加します。このとき\(x\)の増加量は\(3 – 1 = 2\)、
\(y\)の増加量は\(11 – 5 = 6\)なので、変化の割合は\(\frac{6}{2}=3\)となります。
変化の割合は直線の傾きを表す
そしてこの3という数字は直線\(y=3x+2\)の傾きと同じですよね。実はこれ偶然ではなくて、1次関数の変化の割合は直線の傾きを表します。
そして1次関数に関しては\(x\)がどこからどの範囲であっても変化の割合は一定で必ず傾きと等しくなります。
説明では\(x\)が1から3まで増加するときの変化の割合を計算しましたが、これが3から4でも-1から2でも-1000から1000でも変化の割合は必ず3になります。
2次関数の変化の割合って何を表しているの?
それでは2次関数の変化の割合が何を表しているのかを説明します。結論から言うと2次関数の変化の割合は
2次関数上の2点を結ぶ直線の傾き
を表します。
具体的な問題を使って説明します。
問題その1
関数\(y=3x^2\)について、\(x\)の値が-1から3まで増加するときの変化の割合を求めなさい。
この問題では\(x\)が-1から3まで増加するときを考えろと言っていますね。\(y=3x^2\)上の\(x=-1,3\)の点の座標はそれぞれ\((-1,3),(3,27)\)です。
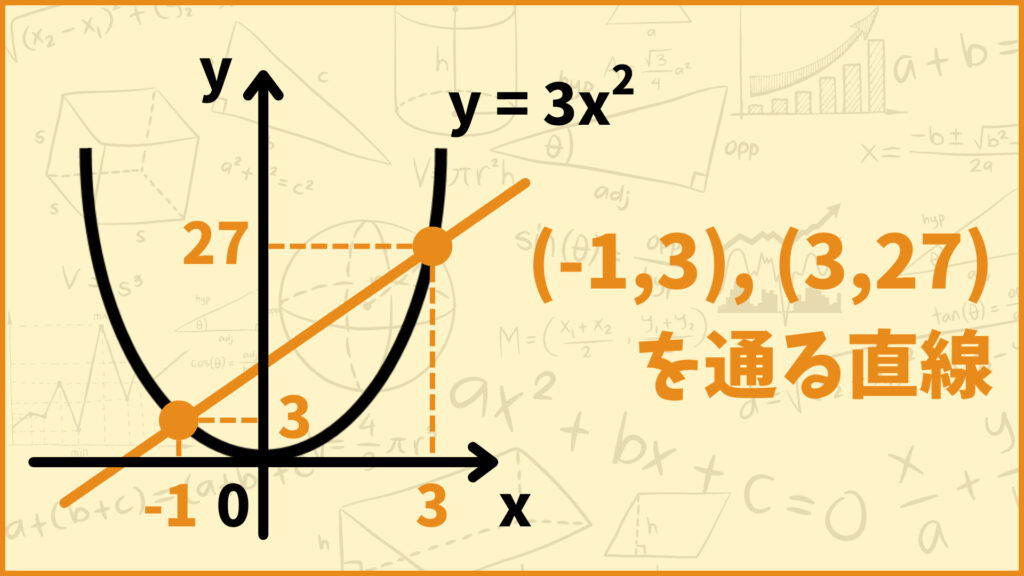
このとき2つの点(-1,3)、(3,27)を通る直線の傾きが変化の割合です。それでは実際に変化の割合を計算してみましょう。変化の割合は
変化の割合 = yの増加量 / xの増加量
で計算できるので、
\(\frac{27-3}{3-(-1)}=\frac{24}{4}=6\)
と計算できます。
「はじめに」の所で言いましたが2次関数の変化の割合は\(a(x_1+x_2)\)でも求めることができます。この公式に当てはめると
\(3(3-1)=6\)
となり上で計算した値と同じになりましたね。この謎の公式が成り立つ理由は第4章の「どうしてあの謎の公式が成り立つの?」の所で説明しています!
問題その2
関数\(y=ax^2\)と\(y=3x+4\)について、\(x\)の値が2から4まで増加するときの変化の割合が等しくなる。このとき\(a\)の値を求めなさい。
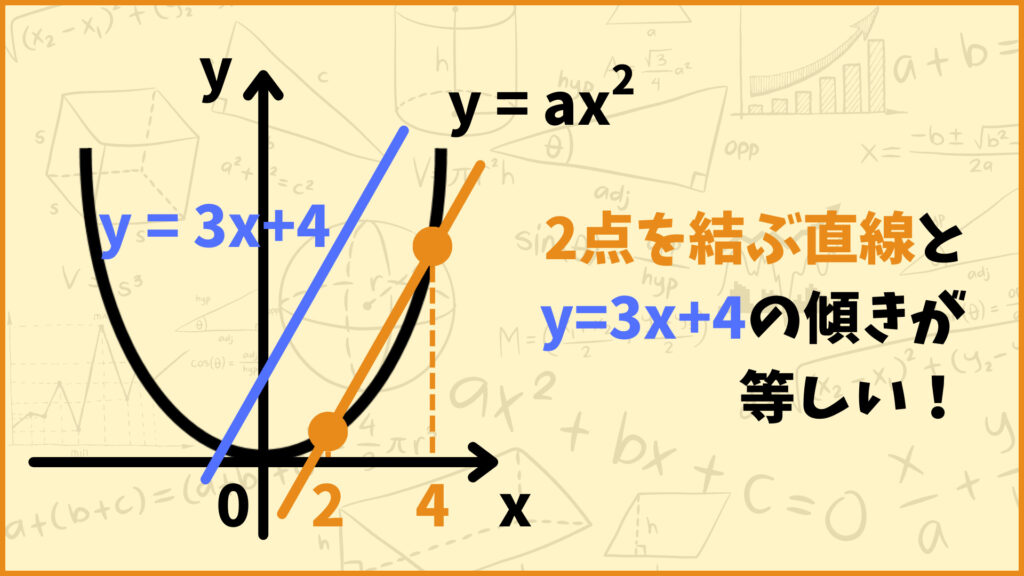
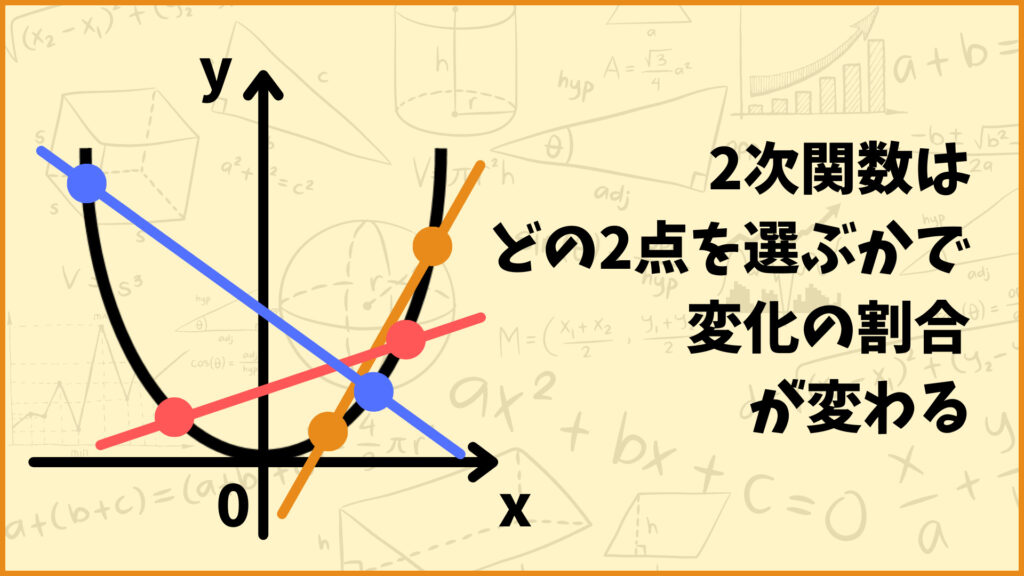
「1次関数の変化の割合」の所で説明したように、1次関数の変化の割合は\(x\)がどこからどこの範囲であっても同じ値を取り、直線の傾きと等しくなります。一方で2次関数の場合は\(x\)がどこからどこの範囲を動くかによって変化の割合が変わります。
ということで問われていることは
\(x\)が2から4に増加するときの\(y=ax^2\)の変化の割合が\(y=3x+4\)の傾き、すなわち3になります。ではこのとき\(a\)の値はなんでしょう?
です。それでは実際に\(a\)の値を求めてみましょう。\(y=ax^2\)について\(x,y\)の増加量を計算して変化の割合を求めることもできますが、結構面倒くさいので\(a(x_1+x_2)\)の公式を使います。
2次関数\(y=ax^2\)の変化の割合:
\(a(2+4)=6a\)
1次関数\(y=3x+4\)の変化の割合:
\(3\)
この2つの値が等しいので
\(6a=3\)
\(a=\frac{1}{2}\)
と言う風に計算できます。
どうしてあの謎の公式が成り立つの?
謎の公式:
\(y=ax^2\)において\(x\)の値が\(x_1\)から\(x_2\)まで増加するときの変化の割合は
\(a(x_1+x_2)\)
で表せる。
それでは最後にどうしてあの謎の公式が成り立つのかを説明したいと思います。
\(x\)が\(x_1\)から\(x_2\)まで増加するときを考えろと言っていますね。\(y=ax^2\)上において\(x=x_1,x_2\)の座標はそれぞれ\((x_1,ax_1^2),(x_2,ax_2^2)\)です。
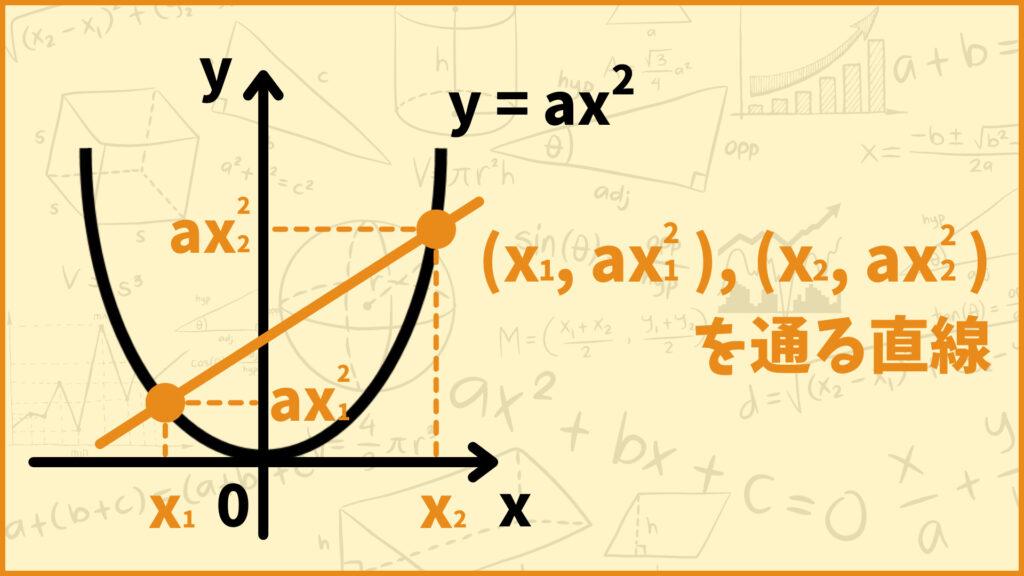
このとき2つの点\((x_1,ax_1^2),(x_2,ax_2^2)\)を通る直線の傾きが変化の割合です。それでは実際に変化の割合を計算してみましょう。変化の割合は
変化の割合 = yの増加量 / xの増加量
で計算できるので、
\(\frac{ax_2^2-ax_1^2}{x_2-x_1}=\frac{a(x_2^2-x_1^2)}{x_2-x_1}=\frac{a(x_2-x_1)(x_2+x_1)}{x_2-x_1}\)
\(=a(x_1+x_2)\)
となり、謎の公式を導出することができました。
おわりに
いかがでしたか。
今回の記事では二次関数の変化の割合について解説していきました。
最後までこの記事を読んでくれてありがとうございました。
普段は大学数学の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。