こんにちは!しゅんです!
この記事ではなぜワーシャルフロイド法でグラフ中の全ての2頂点間の最短距離を求めることができるのかを解説しています。
ワーシャルフロイド法の手順はこちらの記事で詳しく解説しています!
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
ワーシャルフロイド法の手順
まず最初にワーシャルフロイド法の手順を提示します。ワーシャルフロイド法の手順は以下のようになります。
記号の定義
\(G = (V,E)\):有向グラフ
\(d_{ij}^{(k)}\):頂点集合\(V\)の部分集合\(\{1,2,…,k\}\)のみを通れるときの、頂点\(i\)から頂点\(j\)への最短距離
アルゴリズムの手順
STEP 0 グラフの重み付き隣接行列を用意する(最短距離の初期値\(d_{ij}^{(0)}\)の設定)
STEP 1 \(k = 1\)とし、全ての\(i,j \in V\)に対して\(d_{ij}^{(1)}\)を以下のように更新する。
\(d_{ij}^{(1)} = \min\{d_{ij}^{(0)}, d_{i1}^{(0)} + d_{1j}^{(0)}\}\)
STEP 2 \(k = 2\)とし、全ての\(i,j \in V\)に対して\(d_{ij}^{(2)}\)を以下のように更新する。
\(d_{ij}^{(2)} = \min\{d_{ij}^{1)}, d_{i2}^{(1)} + d_{1j}^{(1)}\}\)
STEP 3 \(k = 3\)とし、全ての\(i,j \in V\)に対して\(d_{ij}^{(3)}\)を以下のように更新する。
\(d_{ij}^{(3)} = \min\{d_{ij}^{(2)}, d_{i3}^{(2)} + d_{3j}^{(2)}\}\)
・
・
・
STEP n \(k = n\)とし、全ての\(i,j \in V\)に対して\(d_{ij}^{(n)}\)を以下のように更新する。
\(d_{ij}^{(n)} = \min\{d_{ij}^{(n-1)}, d_{in}^{(n-1)} + d_{nj}^{(n-1)}\}\)
ワーシャルフロイド法の手順はこちらの記事で詳しく解説しています!
なぜワーシャルフロイド法で最短距離を求められるの?
それでは本題に入りましょう。なぜワーシャルフロイド法で全ての2頂点間の最短距離を求めることができるのかを考えてみましょう。重要なポイントは下の式がなぜ成り立つのかということです。
\(d_{ij}^{(k)} = \min\{d_{ij}^{(k-1)}, d_{ik}^{(k-1)} + d_{kj}^{(k-1)}\}\)
このことをメインに考えてみましょう。
上の式は\(k \geq 1\)で使う式で、\(k =0\)のとき\(d_{ij}^{(0)}\)は重み付き隣接行列の\((i,j)\)成分となります。ということで\(k=0\)と\(k \geq 1\)の2つに分けて考えてみましょう。
※グラフは負閉路を持たないとします。
※この記事内で登場する「重み」と「距離」は同じことを表しています。
\(d_{ij}^{(k)}\)の定義
まず最初に\(d_{ij}^{(k)}\)の定義をおさらいしましょう。なぜワーシャルフロイド法が成り立つのかを考える上で\(d_{ij}^{(k)}\)が何を表しているのかをちゃんと理解するのが非常に重要です。\(d_{ij}^{(k)}\)は
「頂点\(i\)から頂点\(j\)へ\(\{1,2,…,k\}\)中の頂点だけ通って良いときの最短距離」
この「\(\{1,2,…,k\}\)中の頂点だけを通って良い」って所が重要です。

上のグラフについて考えてみましょう。例えば\(d_{14}^{(3)}\)を求めようとします。このとき\(d_{14}^{(3)}\)は
「頂点1から頂点4へ頂点1,2,3だけを通って良いときの最短距離」
を表しています。
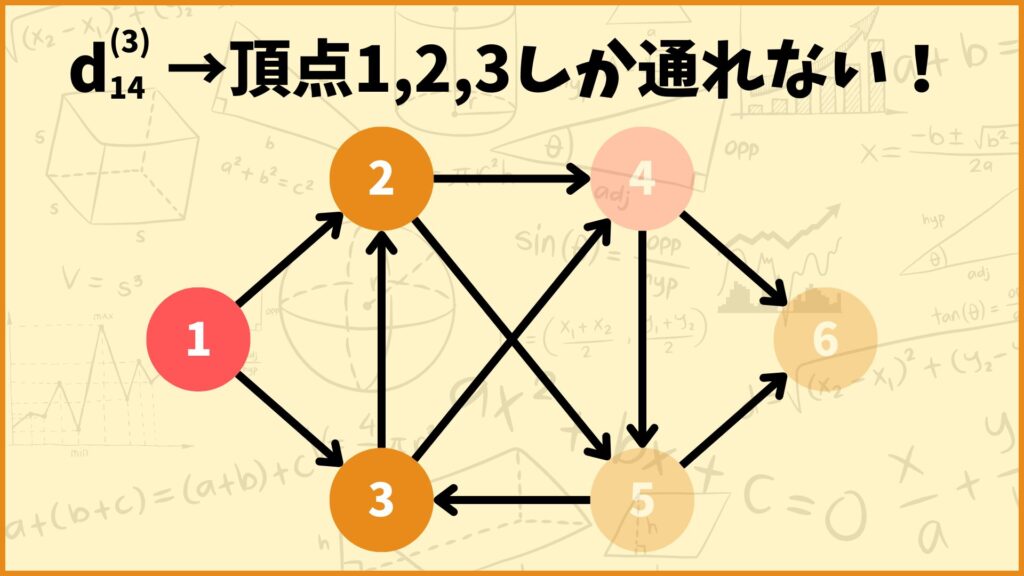
「頂点1,2,3しか通れない」というのは始点から終点へ頂点1,2,3だけを使って通るということなので、始点と終点は頂点1,2,3以外の頂点でも大丈夫です。
\(k=0\)
それでは\(k=0\)のときについて考えてみます。(\(k=0\)のときはほぼ自明です。)\(d_{ij}^{(0)}\)は
「頂点\(i\)から頂点\(j\)へ直接行くとき(途中に通って良い頂点が1つもない場合)の最短距離」
を表します。つまり辺\((i,j)\)があれば\(d_{ij}^{(0)}\)は辺\((i,j)\)の重みとなります。辺\((i,j)\)が無い場合は\(d_{ij}^{(0)} = \infty\)とします。
これって重み付き隣接行列の定義と同じですね。
\(k \geq 1\)
それでは次に\(k \geq 1\)のときについて考えてみましょう。\(k \geq 1\)のときは以下の式が成り立つかどうかを考えます。
\(d_{ij}^{(k)} = \min\{d_{ij}^{(k-1)}, d_{ik}^{(k-1)} + d_{kj}^{(k-1)}\}\)
この式を考えるにあたって、頂点\(i\)から頂点\(j\)へ\(\{1,2,…,k\}\)中の頂点だけを通れるときの最短経路を\(p\)と定義しておきます。
また上の式を考えるために2つのケースについて考えます。1つ目のケースは「\(p\)が頂点\(k\)を含まないとき」で、2つ目のケースは「\(p\)が頂点\(k\)を含むとき」です。
\(p\)が頂点\(k\)を含まないとき
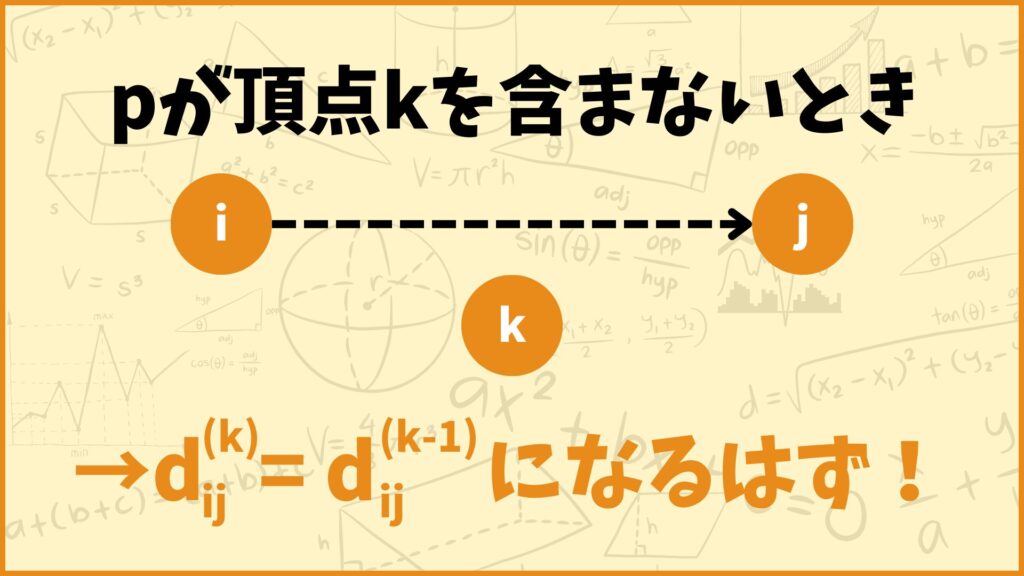
まず最初に\(p\)が頂点\(k\)を含まない場合について考えてみましょう。「\(p\)が頂点\(k\)を含まない」を言い換えると
「\(p\)は\(\{1,2,…,k-1\}\)中の頂点しか通らないときの頂点\(i\)から頂点\(j\)への最短距離」
ということです。これは\(d_{ij}^{(k)}=d_{ij}^{(k-1)}\)であることを表しています。
\(d_{ij}^{(k)}=d_{ij}^{(k-1)}\)
\(p\)が頂点\(k\)を含むとき
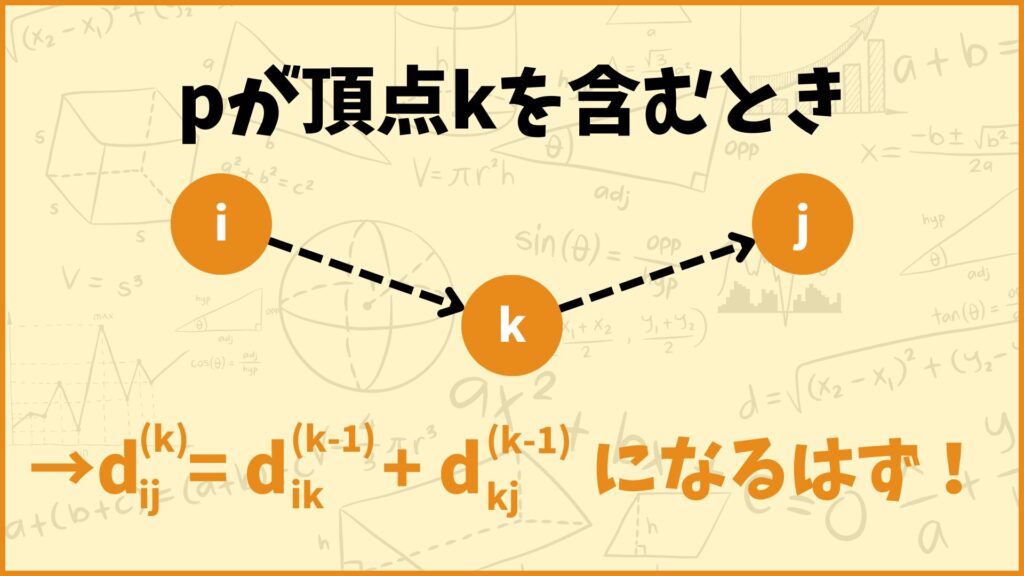
次に\(p\)が頂点\(k\)を含む場合について考えてみましょう。このとき経路\(p\)を2つの経路\(p_1\)と\(p_2\)の経路に分けます。
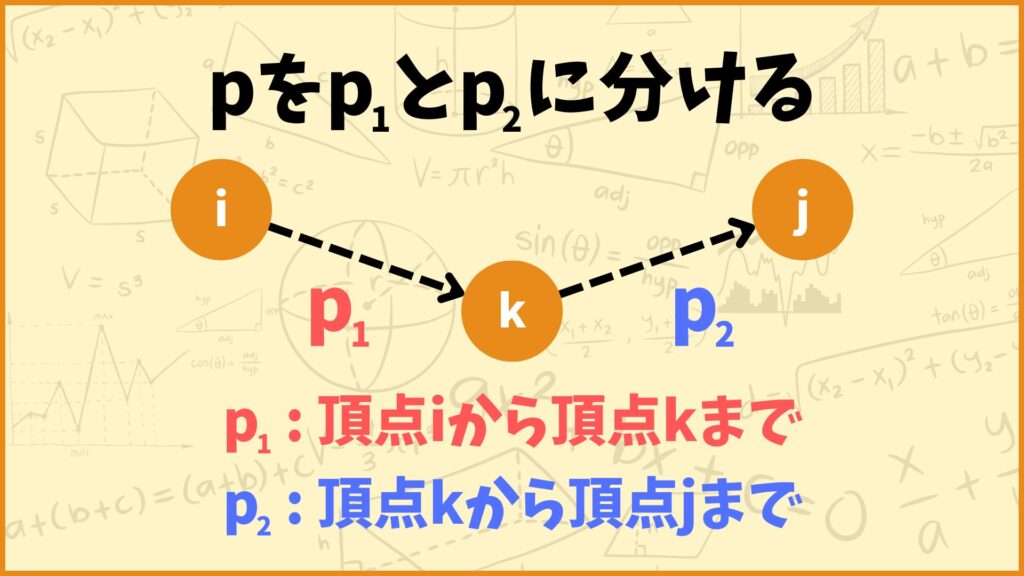
どのように分けるかというと
\(p_1\)は頂点\(i\)から頂点\(k\)までの経路
\(p_2\)は頂点\(k\)から頂点\(j\)までの経路
という風に分けます。ここで1つ重要な点があります。それは
\(p_1\)は頂点\(i\)から頂点\(k\)へ\(\{1,2,…,k-1\}\)中の頂点だけを通れる場合の最短経路
\(p_2\)は頂点\(k\)から頂点\(j\)へ\(\{1,2,…,k-1\}\)中の頂点だけを通れる場合の最短経路
なぜ上記のことが成り立つのかを少し考えてみましょう。まず\(p_1\)について、\(p_1\)が\(\{1,2,…,k-1\}\)中の頂点しか通らないことを示します。経路\(p_1\)は経路\(p\)の一部分なので\(\{1,2,…,k\}\)中の頂点しか通りません。さらにグラフが負閉路を持たない場合、経路\(p\)中に頂点\(k\)は一度しか登場しません。したがって経路\(p_1\)では\(\{1,2,…,k-1\}\)中の頂点しか通りません。
次に\(p_1\)が\(\{1,2,…,k-1\}\)中の頂点しか通らない経路の中で最短経路であることを背理法を使って示します。経路\(p_1\)よりも距離が短い経路\(p’\)があると仮定しましょう。(\(p’\)は頂点\(i\)から頂点\(k\)へ\(\{1,2,…,k-1\}\)中の頂点だけを通れる場合の経路)

そしたら\(\{1,2,…,k\}\)中の頂点だけを通れる場合の\(i-j\)路に関して、経路\(p\)より経路\(p’\)を通って頂点\(k\)を通って経路\(p_2\)を通る経路の方が距離が短いことになっていしまいます。これは\(p\)が最短経路であることに矛盾します。
経路\(p_2\)に関しても同じように考えることができます。以上のことから上記の事実が成り立ちます。
つまり経路\(p_1\)の距離は\(d_{ik}^{(k-1)}\)で経路\(p_2\)の距離は\(d_{kj}^{(k-1)}\)ということが言えます。
経路\(p\)の距離は経路\(p_1\)と\(p_2\)の距離の合計なので、これを数式で表すと以下のように表せます。
\(d_{ij}^{(k)} = d_{ik}^{(k-1)} + d_{kj}^{(k-1)}\)
おわりに
いかがでしたか。
今回の記事ではワーシャルフロイド法について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。




