こんにちは!しゅんです!
今回の記事ではクラス編成問題を整数計画問題として定式化してpythonで解く方法を解説していきます!
クラス編成問題とは、例えば大学でどの学生がどの授業を受講するかを決める問題です。
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
問題設定
A大学のB学科には200人の学生が在籍している。ある学期にB学科では6つの選択必修授業が開講され、学生は6つの授業の中から必ず1つ履修する必要がある。各授業は履修人数の上限が決まっており、以下の通りである。
授業1 : 30人
授業2 : 60人
授業3 : 20人
授業4 : 40人
授業5 : 25人
授業6 : 50人
各学生はどの授業を履修したいかの評価をつける。
(2:履修したい、1:どっちでも良い、0:履修したくない)
目標:
学生から不満が出ないようなクラスを編成する。
今回は上記のような問題設定を考えていきます。このようなクラス編成問題を整数計画問題として定式化する上で重要な点をピックアップして、もう少し詳しく解説していきます。
学生は必ず1つ履修する必要がある

「学生は必ず1つ履修する必要がある」というのは制約条件として記述する必要があります。授業を1つも取らない学生や、授業を2つ以上取る学生が存在してはいけません。
各授業の履修人数の上限が決まっている
履修人数の上限:
授業1 : 30人
授業2 : 60人
授業3 : 20人
授業4 : 40人
授業5 : 25人
授業6 : 50人
「各授業の履修人数の上限が決まっている」というのも制約条件として記述する必要があります。履修人数の上限なので、別にこの値を超えなければ何人でも良いです。
クラス編成の例:
授業1 : 30人
授業2 : 55人
授業3 : 20人
授業4 : 35人
授業5 : 15人
授業6 : 45人
例えば上記のようなクラス編成はOKです。授業1、授業3は履修人数が上限値になっていて、授業2、授業4、授業5、授業6には上限値を下回っています。
各授業の上限値の合計は225なので、B学科の学生数より少しだけ余裕を持たせました。
各学生はどの授業を履修したいかの評価をつける
評価の例(2:履修したい、1:どっちでも良い、0:履修したくない)
授業1 : 2
授業2 : 1
授業3 : 0
授業4 : 1
授業5 : 2
授業6 : 1
「各学生はどの授業を受講したいかの評価をつける」というのは、目的関数を設定するのに使います。各学生は6つの授業に対し、どれくらい履修したいかを3段階で評価します。(2:履修したい、1:どっちでも良い、0:履修したくない)
上記にあるのは評価の例です。このように各学生は各授業に対し評価をつけます。
履修人数の上限があるため、必ず履修したい授業を履修できる訳ではありません。
学生から不満が出ないようなクラスを編成する
今回の問題の目的は「学生から不満が出ないようなクラスを編成する」というものです。学生は各授業に評価をつけているので、つまり学生の評価をなるべく考慮したクラスを編成するのを目的とします。
今回は超単純に
「実際に履修する授業に対する評価値の合計を最大とする」
ことを目的としたいと思います。

例えば学生1、学生2、学生3がそれぞれ授業1、授業2、授業5を履修するとします。また学生1は授業1に対して評価0、学生2は授業2に対して評価2、学生3は授業5に対して評価2としているとします。
このとき3人の学生の評価値の合計は
\(0+2+2=4\)
となります。直観的にはこの値が大きい程、学生皆が満足していると捉えることができます。ということで今回は履修する授業に対する評価値の合計が最大になるようなクラス編成をしたいと思います。
整数計画問題として定式化する
それでは次にクラス編成問題を整数計画問題として定式化する方法を説明します。「記号の定義」、「目的関数の設定」、「制約条件の設定」の3つに分けてそれぞれ説明したいと思います。
記号の定義
パラメータ:
\(S\) : 学生の集合
\(C\) : 授業の集合
\(u_c\) : 授業\(c\)の履修人数の上限
\(v_{sc} \in \{0,1,2\}\) : 学生\(s\)の授業\(c\)に対する評価
変数:
\(x_{sc} \in \{0,1\}\) : 学生\(s\)を授業\(c\)に割り当てるなら1、そうでないなら0を取る0-1変数
パラメータとして\(S,C,u_c,v_{sc}\)を設定します。\(S\)は学生の集合です。今回の例だと学生数は200人なので
\(S = \{1,2,…,200\}\)
となります。
\(C\)は授業の集合です。今回は6つの授業があるので
\(C = \{1,2,3,4,5,6\}\)
となります。
\(u_c\)は授業\(c\)の履修人数の上限です。今回の場合
\(u_1=30,u_2=60,u_3=20,u_4=40,u_5=25,u_6=50\)
となります。
\(v_{sc}\)は学生\(s\)の授業\(c\)に対する評価です。例えば学生1の授業6に対する評価が2のとき、
\(v_{16} = 2\)
となります。
目的関数の設定
目的関数:
\(\sum\limits_{s \in S}\sum\limits_{c \in C}v_{sc}x_{sc}\)
今回のクラス編成問題の目的は
「評価値の合計が最大となるクラスを編成する」
というものです。
学生1 → 授業2 (評価2)
学生2 → 授業1 (評価1)
学生3 → 授業1 (評価0)
学生4 → 授業5 (評価2)
例えば学生数が4人\((|S|=4)\)だとします。上記のように学生1,2,3,4がそれぞれ授業2,1,1,5に割り当てられ、また割り当てられた授業に対する各学生の評価がそれぞれ2,1,0,2のとき、さっきの目的関数の値は
\(\sum\limits_{s \in S}\sum\limits_{c \in C}v_{sc}x_{sc} = v_{12}+v_{21}+v_{31}+v_{45}=2+1+0+2=5\)
となり、この値は割り当てられた授業に対する各学生の評価値の合計と対応します。今回はこの目的関数が最大となる場合を求めます。
目的関数(最大化):
\(\sum\limits_{s \in S}\sum\limits_{c \in C}v_{sc}x_{sc}\)
制約条件の設定
制約条件:
\(\sum\limits_{c \in C}x_{sc} = 1 \;\;\; (\forall s \in S)\)
\(\sum\limits_{s \in S}x_{sc} \leq u_c \;\;\; (\forall c \in C)\)
1つずつ説明していきます。
1つ目の制約条件
1つ目の制約条件:
\(\sum\limits_{c \in C}x_{sc} = 1 \;\;\; (\forall s \in S)\)
1つ目の制約は
「各学生は必ず1つの授業に割り当てられる」
ということを表しています。例えば学生1についてこの制約条件考えてみましょう。制約式は
\(\sum\limits_{c \in C}x_{1c} =x_{11}+x_{12}+x_{13}+x_{14}+x_{15}+x_{16}= 1\)
これは\(x_{11},x_{12},…,x_{16}\)の中でどれか1つだけが1になるということです。例えば\(x_{13}=1\)だとしましょう。これは
「学生1は授業3に割り当てられる」
ということを表しています。このとき\(x_{11}=x_{12}=x_{14}=x_{15}=x_{16}=0\)なので授業3以外の授業へは割り当てられていないです。つまり学生1は1つの授業にしか割り当てられていないことになります。
この制約が全ての学生について存在すれば良いので\((\forall s \in S)\)で全ての学生に対してこの制約を設定しています。
1つ目の制約条件:
\(\sum\limits_{c \in C}x_{sc} = 1 \;\;\; (\forall s \in S)\)
2つ目の制約条件
2つ目の制約条件:
\(\sum\limits_{s \in S}x_{sc} \leq u_c \;\;\; (\forall c \in C)\)
2つ目の制約条件は
「各授業の履修人数は上限値を超えない」
ということを表しています。例えば授業1についてこの制約条件を考えてみましょう。\(u_1=30\)なので制約式は
\(\sum\limits_{s \in S}x_{s1} = x_{11}+x_{21}+…+x_{2001} \leq 30\)
となります。これは\(x_{11},x_{21},…,x_{2001}\)の中で最大でも30個しか1を取れないということを表しています。つまり授業1を履修できる人数は最大でも30人であることを表しています。
この制約が全ての授業について存在すれば良いので\((\forall c \in C)\)で全ての授業に対してこの制約を設定しています。
2つ目の制約条件:
\(\sum\limits_{s \in S}x_{sc} \leq u_c \;\;\; (\forall c \in C)\)
整数計画問題としてまとめる
以上のことを踏まえて整数計画問題として定式化しましょう。
パラメータ:
\(S\) : 学生の集合
\(C\) : 授業の集合
\(u_c\) : 授業\(c\)の履修人数の上限
\(v_{sc} \in \{0,1,2\}\) : 学生\(s\)の授業\(c\)に対する評価
変数:
\(x_{sc} \in \{0,1\}\) : 学生\(s\)を授業\(c\)に割り当てるなら1、そうでないなら0を取る0-1変数
目的関数(最大化):
\(\sum\limits_{s \in S}\sum\limits_{c \in C}v_{sc}x_{sc}\)
制約条件:
\(\sum\limits_{c \in C}x_{sc} = 1 \;\;\; (\forall s \in S)\)
\(\sum\limits_{s \in S}x_{sc} \leq u_c \;\;\; (\forall c \in C)\)
\(x_{sc} \in \{0,1\} \;\;\; (\forall s \in S, \; \forall c \in C)\)
ということで整数計画問題として定式化することができました。
pythonで解いてみた
それでは実際にこの問題をpythonで解いてみましょう。結論以下のプログラムを実行することで問題を解くことができます。
## 事前準備
from pulp import * # pulpをインポート
import pandas as pd # pandasをインポート
import random # randomをインポート
random.seed(1) # 毎回同じ乱数が生成されるようにする
## 記号の設定
S = [s for s in range(200)] # 学生のリスト
C = [c for c in range(6)] # 授業のリスト
v = [[0 for _ in C] for _ in S] # 学生の授業に対する評価の初期リスト
for s in S:
for c in C:
v[s][c] = random.randint(0,2) # 0,1,2のいずれかをランダムに出力
u = [30,60,20,40,25,50] # 各授業の履修人数の上限値のリスト
## 整数計画問題として定式化したものを解く
prob = pulp.LpProblem(sense = LpMaximize) # 問題を最大化に設定
x = LpVariable.dicts("x", (S,C), cat="Binary") # 変数を設定
prob += lpSum(v[s][c]*x[s][c] for s in S for c in C) # 目的関数を設定
# 制約条件を設定
for s in S:
prob += lpSum(x[s][c] for c in C) == 1 # 各学生は必ず1つ授業に割り当てられる
for c in C:
prob += lpSum(x[s][c] for s in S) <= u[c] # 各授業の履修人数は上限値を超えない
result = prob.solve() # 問題を解く
## 結果の表示
print("解の状態 :", LpStatus[result]) # 解の状態を表示
print("最適値 :", prob.objective.value()) # 最適値の表示
# 最適解の表示(値が1の変数だけ表示)
for s in S:
for c in C:
if x[s][c].value() == 1:
print(f"x_学生{s+1}_授業{c+1}")
このプログラムを実行したら上の結果が得られました。それではコードが何を表しているのか、そして得られた結果の見方について1つずつ解説していきます。
コードの解説
「事前準備」、「記号の設定」、「整数計画問題として定式化して解く」、「結果の表示」の4つに分けてそれぞれ解説していきます。
事前準備
## 事前準備
from pulp import * # pulpをインポート
import pandas as pd # pandasをインポート
import random # randomをインポート
random.seed(1) # 毎回同じ乱数が生成されるようにする
ここではpulp,pandas.randomをインポートし、毎回同じ乱数が生成されるようにしています。
pulpはpythonで整数計画問題を扱うために使います。
pandasは問題を解くこと自体には使いませんが、結果を見やすく表示するために使います。
randomはpythonで乱数を扱うために使います。
「random.seed()」でプログラムの実行時に毎回同じ乱数が生成されるようにします。(これ書かないと毎回結果が変わってしまいます。)
記号の設定
## 記号の設定
S = [s for s in range(200)] # 学生のリスト
C = [c for c in range(6)] # 授業のリスト
v = [[0 for _ in C] for _ in S] # 学生の授業に対する評価の初期リスト
for s in S:
for c in C:
v[s][c] = random.randint(0,2) # 0,1,2のいずれかをランダムに出力
u = [30,60,20,40,25,50] # 各授業の履修人数の上限値のリスト
2行目で学生の集合を設定しています。
3行目で授業の集合を設定しています。
4行目で学生の授業に対する評価の初期リストを設定しています。5行目以降でこのリスト中の要素をどんどん更新していきます。
5~7行目で評価値を設定しています。今回は評価値をランダムに設定しています。「random.randint(0,2)[/latex]で0,1,2のいずれかの値をランダムに出力できます。
8行目で各授業の履修人数の上限値のリストを設定しています。
pythonでは数字が0から始まっていることに注意してください。のちに説明しますがこれにより解を表示するときはs+1,c+1を表示するようにしています。
整数計画問題として定式化して解く
## 整数計画問題として定式化したものを解く
prob = pulp.LpProblem(sense = LpMaximize) # 問題を最大化に設定
x = LpVariable.dicts("x", (S,C), cat="Binary") # 変数を設定
prob += lpSum(v[s][c]*x[s][c] for s in S for c in C) # 目的関数を設定
# 制約条件を設定
for s in S:
prob += lpSum(x[s][c] for c in C) == 1 # 各学生は必ず1つ授業に割り当てられる
for c in C:
prob += lpSum(x[s][c] for s in S) <= u[c] # 各授業の履修人数は上限値を超えない
result = prob.solve() # 問題を解く
2行目で問題を最大化に設定しています。「sense = LpMinimize」だと目的関数を最小化する問題に設定できます。
3行目で変数を設定しています。「LpVariable.dicts()」は変数をいっぺんに設定できるので変数が多いときに便利です。括弧の中身は左から順に(”変数名”, 添字の集合, 変数の種類)となっています。
変数\(x_{sc}\)の添字はそれぞれ\(s\)が集合\(S\)、\(c\)が集合\(C\)中の要素なので添字の集合は(S,C)とします。
「cat = “Binary”」で変数を0-1変数に設定しています。連続変数にしたければ「cat = “Continuous”」とします。
4行目で目的関数を設定しています。pulpで\(\sum\)は「lpSum」で表現できます。「x[s][c]」と設定することで\(x_{sc}\)、「for s in S for c in C」と設定することで\(s \in S,c \in C\)を表現できます。
6~9行目で制約条件を設定しています。6~7行目で1つ目の制約条件、8~9行目で2つ目の制約条件をそれぞれ設定しています。
10行目で問題を解いています。問題を解くときは「.solve()」でできます。
結果の表示
## 結果の表示
print("解の状態 :", LpStatus[result]) # 解の状態を表示
print("最適値 :", prob.objective.value()) # 最適値の表示
# 最適解の表示(値が1の変数だけ表示)
for s in S:
for c in C:
if x[s][c].value() == 1:
print(f"x_学生{s+1}_授業{c+1}")
2行目で解の状態を表示しています。Optimalと表示されたら最適解が得られています。
3行目で最適値を表示しています。
5~8行目で最適解を表示しています。値が1の変数だけ表示するようにしています。「f”x_学生{s+1}_授業{c+1}”」としているのはリストS,Cが0から始まるからです。数字がずれても特に問題はないですが、これまでの説明と合わせるために「s」,「c」ではなく「s+1」,「c+1」としています。
結果の解釈

上記のプログラムを実行したら上のような結果が得られました。1つずつ見ていきます。
1行目は解の状態を表しています。Optimalと表示されているので最適解が得られています。
2行目は最適値を表しています。今回のクラス編成問題の最適値は379であることが分かりました。
3行目以降は最適解を表しています。実際はこの解が200個列挙されますが、全てを見せることはできないので上の方だけ見せています。これを見ると例えば学生1は授業2に割り当てられたようです。
もう少し詳しく結果を見てみましょう。
各授業の履修人数
まずは各授業の履修人数を見てみましょう。
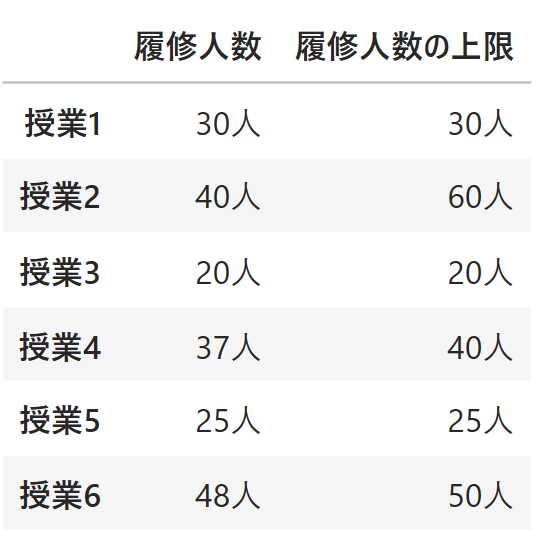
上の表は1行目が最適解における各授業の履修人数、2行目が各授業の履修人数の上限をそれぞれ表しています。例えば授業1を履修する学生数が30人で、上限値ぴったりあることが分かります。
この表を見ると、どの授業も履修人数がちゃんと上限値を超えていないことが分かります。
上の表を表示するコードは以下の通りです。本題ではないので説明は省略します。
NoP = [[0 for _ in range(2)] for _ in C]
for c in C:
for s in S:
if x[s][c].value() == 1:
NoP[c][0] += 1
NoP[c][0] = str(NoP[c][0]) + "人"
NoP[c][1] = str(u[c]) + "人"
df_NoP = pd.DataFrame(NoP, index = [f"授業{c+1}" for c in C], columns = ["履修人数","履修人数の上限"])
df_NoP学生が希望の授業に割り当てられているかを見てみる
次に従業員が希望の勤務に出勤できているかを確かめてみましょう。

上の表は評価値別の割当人数を表しています。例えば評価:0の行は1人と書いてありますが、これは0と評価した授業に割り当てられた学生数が1人だったことを表しています。
これを見ると9割の学生が評価2、つまり「履修したい」と評価した授業を履修することができています。
0と評価した授業に割り当てられている学生が1人いますね。この人の評価リストを確認してみましょう。
## 0と評価した授業に割り当てられた学生の評価リストを表示するコード
for s in S:
for c in C:
if x[s][c].value() == 1:
if v[s][c] == 0:
print(f"学生{s+1}の評価リスト :",v[s])
これを見ると学生164は全ての授業を履修したくないと評価している学生でした。この学生が評価0の授業に割り当てられるのはしょうがないので、履修したくない授業に割り当てられた人は実質いないと考えて良さそうですね。
上の表を表示するコードは以下の通りです。本題ではないので説明は省略します。
NoV = [0 for _ in range(3)]
for s in S:
for c in C:
if x[s][c].value() == 1:
NoV[v[s][c]] += 1
for i in range(len(NoV)):
NoV[i] = str(NoV[i]) + "人"
df_NoV =pd.DataFrame(NoV, index = [f"評価 : {v}" for v in range(3)], columns = ["評価値別の割当人数"])
df_NoVおわりに
いかがでしたか。
今回の記事ではクラス編成問題について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。



