- コラッツ予想ってなに?
- コラッツ予想の計算をpythonで実装したい…
- コラッツ予想の計算過程をグラフで確認したい…
こんにちは!しゅんです!
今回の記事ではコラッツ予想の計算をpythonで実装してみました。
コラッツ予想は未解決問題の1つで、解けたら1億2000万もらえるらしいです。ただ問題の内容や計算式は簡単に理解できるので、この記事ではコラッツ予想で登場する計算をpythonで実装してみたいと思います。
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
今回解説したものをstreamlitでwebアプリ化しました!このwebアプリでは実際に数字を入力したら計算過程を表示してくれます。
コラッツ予想ってなに?
コラッツ予想:
どんな正の整数に対しても以下の操作
・その数字が偶数なら2で割る。
・その数字が奇数なら3をかけて1を足す。
を続けていけば、必ず1になる。
具体例を使って確認してみましょう。例えば6に対して上の操作を行います。
6は偶数なので2で割ります。
\(6 \div 2 =3\)
3は奇数なので3をかけて1を足します。
\(3 \times 3+1 = 10\)
10は偶数なので2で割ります。
\(10 \div 2= 5\)
5は奇数なので3をかけて1を足します。
\(5 \times 3 + 1 = 16\)
16は偶数なので2で割ります。
\(16 \div 2 = 8\)
8は偶数なので2で割ります。
\(8 \div 2 = 4\)
4は偶数なので2で割ります。
\(4 \div 2 = 2\)
2は偶数なので2で割ります。
\(2 \div 2 = 1\)
ということで1になりました。
6の場合:6→3→10→5→16→8→4→2→1
これが全ての正の整数に対して成り立つという主張がコラッツの予想です。
pythonで実装する
それではこの計算をpythonで実装してみましょう。結論以下のコードになります。
def Collatz(n): # 関数として定義する
result = [n] # 結果の初期リスト
while n != 1: # nが1になるまで操作を続ける
if n%2 == 1: # nが奇数の場合
n = 3*n + 1 # 3をかけて1を足す
else: # nが偶数の場合
n = n / 2 # 2で割る
result.append(int(n)) # 計算した値をresultに追加する
return result # 結果を返す
今回は関数として定義しました。いくつか数字を入力して結果を見てみましょう。
Collatz(6) # 6の場合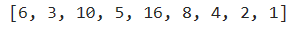
Collatz(7) # 7の場合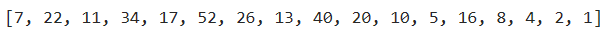
Collatz(11111111111) # 11111111111の場合
それではコードが何を表しているかを1つずつ解説していきます。
1行目の説明
def Collatz(n): # 関数として定義する
1行目で関数の定義をしています。
def 関数名(引数)の形で関数を定義します。
今回は「Collatz」という名前の関数を作ります。引数は「n」です。「Collatz(7)」って実行したら「n=7」、「Collatz(100)」って実行したら「n=100」として計算します。
2行目の説明
def Collatz(n): # 関数として定義する
result = [n] # 結果の初期リスト
今回は最終的に計算して得られた数字の列を返す関数を作りたいので、2行目ではその列の初期リストを作成しています。初めはnからスタートするのでnをリストに入れておきます。
3行目の説明
def Collatz(n): # 関数として定義する
result = [n] # 結果の初期リスト
while n != 1: # nが1になるまで操作を続ける
3行目では、nが1になるまで操作を続けることを表しています。
while文は「while 条件」の形で使います。条件が成立している間は操作を続けるという意味です。
nが1じゃない間は操作を続けたいので「n != 1」としています。
4~5行目の説明
def Collatz(n): # 関数として定義する
result = [n] # 結果の初期リスト
while n != 1: # nが1になるまで操作を続ける
if n%2 == 1: # nが奇数の場合
n = 3*n + 1 # 3をかけて1を足す
4~5行目では「nが奇数の場合は3をかけて1を足す」という操作をしています。
「n%2」はnを2で割ったあまりを表しています。nが奇数であることとn%2が1であることは同値なので「if n%2 == 1:」とif文を使っています。
「n = 3*n + 1」はnに3をかけて1を足すという操作をしています。
6~7行目の説明
def Collatz(n): # 関数として定義する
result = [n] # 結果の初期リスト
while n != 1: # nが1になるまで操作を続ける
if n%2 == 1: # nが奇数の場合
n = 3*n + 1 # 3をかけて1を足す
else: # nが偶数の場合
n = n / 2 # 2で割る
6~7行目では「nが偶数の場合は2で割る」という操作をしています。
「else:」は「さっきのif文の条件を満たさない場合」と言う意味です。今回で言えばnが偶数の場合を表しています。
「n = n / 2」でnを2で割っています。
8行目の説明
def Collatz(n): # 関数として定義する
result = [n] # 結果の初期リスト
while n != 1: # nが1になるまで操作を続ける
if n%2 == 1: # nが奇数の場合
n = 3*n + 1 # 3をかけて1を足す
else: # nが偶数の場合
n = n / 2 # 2で割る
result.append(int(n)) # 計算した値をresultに追加する
8行目では、resultに計算して得られた値を追加しています。リストに要素を追加する場合は「.append(追加したい要素)」を使います。今回はnを追加したいので「int(n)」と書いています。
「n」が偶数の時に「n = n / 2」という計算をしますが、この操作で得られる「n」はfloat型です。
a = 4/2
print(a)
print(type(a))
上のコードは「4/2」の値と型を表示するコードです。これを見ると4/2の値が2.0になっておりfloat型になっていることが分かります。このようにpythonではたとえ割り切れても整数で返されるわけではないです。
nを整数にしたければ「int(n)」とすればOKです。そのためresultに追加する要素は「n」ではなく「int(n)」としています。
9行目の説明
def Collatz(n): # 関数として定義する
result = [n] # 結果の初期リスト
while n != 1: # nが1になるまで操作を続ける
if n%2 == 1: # nが奇数の場合
n = 3*n + 1 # 3をかけて1を足す
else: # nが偶数の場合
n = n / 2 # 2で割る
result.append(int(n)) # 計算した値をresultに追加する
return result # 結果を返す
9行目でresultを返しています。resultは計算結果を表すリストです。例えば「n = 」6のときresultは以下のようになります。
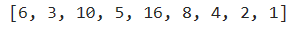
これは1になるまで操作を続けると、6→3→10→5→16→8→4→2→1となることを表しています。
どんな挙動かをグラフを使って確認する
最後にコラッツ予想において各操作で得られる値がどのように変化するかをグラフを使って確認してみましょう。以下のコードを実行することでグラフを描画できます。
import matplotlib.pyplot as plt # matplotlibをインポート
y = Collatz(97) # n = 97のときを計算
x = [i for i in range(1,len(y)+1)] # 操作回数のリスト
plt.figure(figsize = (20,5)) # グラフのサイズを設定
plt.plot(x,y, marker="o", color = "slateblue") # 折れ線グラフを描画
max_y = max(y) # yの最大値を計算
plt.text(x[-1] - 15, max_y - 1000, f'Max: {max_y}', fontsize=30, color = "slateblue") # グラフ上にyの最大値をテキストとして追加
plt.show()
上のグラフはn=97のときを表しています。横軸が操作回数、縦軸が各操作によって得られた値の大きさを表しています。右上のMaxは最大値を表しています。
Max: 9232となっているのでn=97のとき最大で9232まで値が大きくなるということが分かります。
おわりに
いかがでしたか。
今回の記事ではコラッツ予想についてpythonで実装していきました。
今後もこのような数学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。



