- 2値分類モデルの精度って、どうやって評価すればいいの?
- AccuracyやF1 scoreって、いったい何が違うの?
- Confusion Matrixの見方って、難しそうでよくわからない…
- Accuracy : 全データの中で正しく予測できた割合
- Precision : Aと予測したデータの中で、実際にAだった割合
- Recall : 実際にAのデータのうち、Aと予測できた割合
- F1 score : PrecisionとRecallの調和平均
\(\text{Accuracy} = \frac{\text{TP}+\text{TN}}{\text{TP}+\text{FP}+\text{FN}+\text{TN}}\)
\(\text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}}\)
\(\text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}}\)
\(\text{F1 score} = 2\times\frac{\text{Preision}\times\text{Recall}}{\text{Precision}+\text{Recall}}\)

はじめに
こんにちは!しゅんです!今回は2値分類でよく登場する、Accuracy, F1 score, Confusion Matrixについて解説していきます。
機械学習を勉強していると、2値分類の評価指標としてAccuracyやF1 scoreやConfusion Matrixという単語に遭遇すると思います。この記事ではこれらの単語が何を表しているのか、どうやって使うのかを解説していきます。
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
2値分類ってなに?
2値分類をザックリ説明すると
「データを2つのグループに分けること」
です。例えば上図のように、画像を見てその画像が犬なのか犬じゃないのか見分けることは2値分類の例となります。2値分類はいろいろな場面で登場し、上の例の他にも
・異常検知(このネジには傷があるかないか)
・スパムメールの判断(このメールはスパムかスパムじゃないか)
・顔認証システム(この顔は登録された顔かそうでないか)
などがあります。このようなタスクをAIで解決しようという試みが現在さまざまな所で行われています。
2値分類ができる分析手法はたくさんあるので、分析をする上でどんな手法を使えば良いのかを考える必要があります。その際非常に重要なのが、
「どれくらいの精度で分類できるのか」
ということです。例えば与えられた画像が犬の画像なのか犬の画像じゃないのかを見分ける2値分類をしたとき、
手法1では100枚中50枚見分けられた
手法2では100枚中85枚見分けられた
手法3では100枚中75枚見分けられた
となったら、直観的には手法2を採用するのが一番良さそうです。このように2値分類を行う上で、どれくらいの精度で分類できるのかというのは非常に重要な指標です。
この後に説明するAccuracy, Confusion Matrix, F1 scoreは全て精度に関係する用語です。
Accuracyってなに?
Accuracyの計算方法

Accuracyの計算方法は
\(\text{Accuracy} = \text{正解したデータの数} / \text{データの数}\)
で、分析手法の精度を測る上で基本中の基本と言える指標です。例えば100枚の画像データが与えられ、そのうち80枚の画像は、正しく犬か犬じゃないかを当てることができたとします。このときのAccuracyは
\(\text{Accuracy} = 80 / 100 = 0.8\)
と計算できます。直観的にはAccuracyが高いほど精度が良いと言えそうですね。
Accuracyの問題点
ついさっき、直観的にはAccuracyが高いほど精度が良いと言えそうって話しましたが、必ずしもそうとは限りません。例えば以下の2つのパターンについて考えてみます。いずれも100枚の画像を分類した結果を表しています。

パターン1:犬の画像50枚中40枚、犬じゃない画像50枚中40枚分類できた。
パターン2:犬の画像20枚中5枚、犬じゃない画像80枚中75枚分類できた。
この2つのパターンではいずれも100枚中80枚のデータを正しく分類できているので、Accuracyの値はいずれも0.8となります。ただパターン1では犬の画像も犬じゃない画像もいい感じに分類できていますが、パターン2ではほとんど犬の画像を犬だと分類できていないです。
パターン2のような場合には、単純にAccuracyだけでその手法の精度を決めるのは良くないです。そのため別の指標を使って精度を評価する必要があります。
Confusion Matrixってなに?
Confusion Matrixをザックリ説明すると
「分類結果をまとめた表」
となります。具体例を使って説明します。
具体例を使って説明する

上図の例を見てみましょう。上図は100枚の画像を2値分類したときの結果を表しています。上図の結果は
・100枚の画像のうち、50枚は犬の画像で残りの50枚は犬じゃない画像である。
・50枚の犬の画像のうち、正しく犬と予測できたのは40枚で、残りの10枚は犬じゃないと予測した。
・50枚の犬じゃない画像のうち、正しく犬じゃないと予測できたのは40枚で、残りの10枚は犬と予測した。
ということを表しています。これを文字で表すとこんなに長いですが、上のように表でまとめると非常にスッキリします。この表をConfusion Matrix(日本語だと混同行列)と言います。

次に上の表を見てみましょう。上の表は
・100枚の画像のうち、20枚は犬の画像で残りの80枚は犬じゃない画像である。
・20枚の犬の画像のうち、正しく犬と予測できたのは5枚で、残りの15枚は犬じゃないと予測した。
・80枚の犬じゃない画像のうち、正しく犬じゃないと予測できたの75枚で、残りの5枚は犬と予測した。
ということを表しています。この例も先ほどの例もAccuracyの値はどちらも0.8ですが、Confusion Matrixを見ると中身が全然違いますね。このようにConfusion Matrixを見れば同じAccuracyの値でも違いが見えたりします。
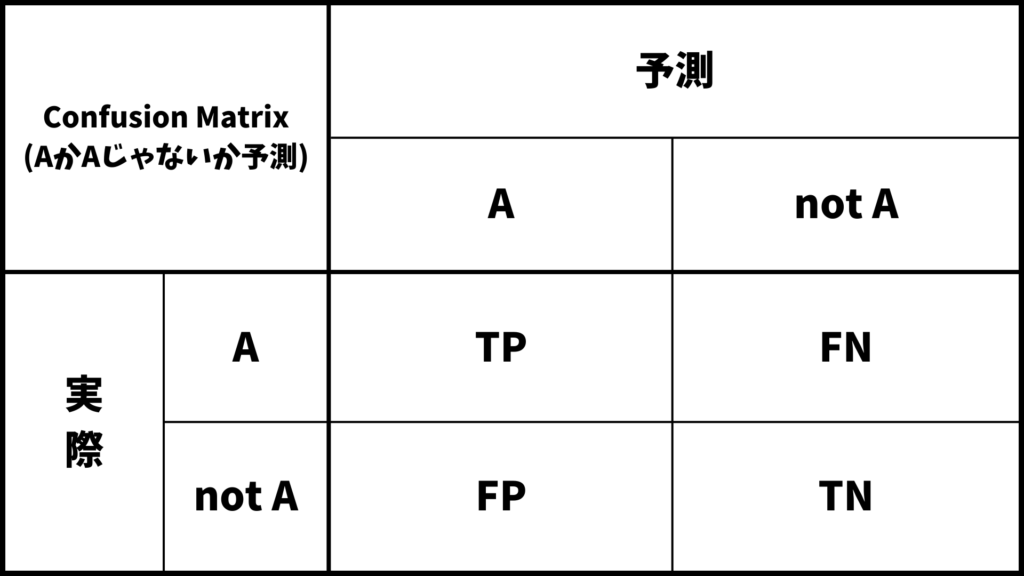
より一般的に説明する
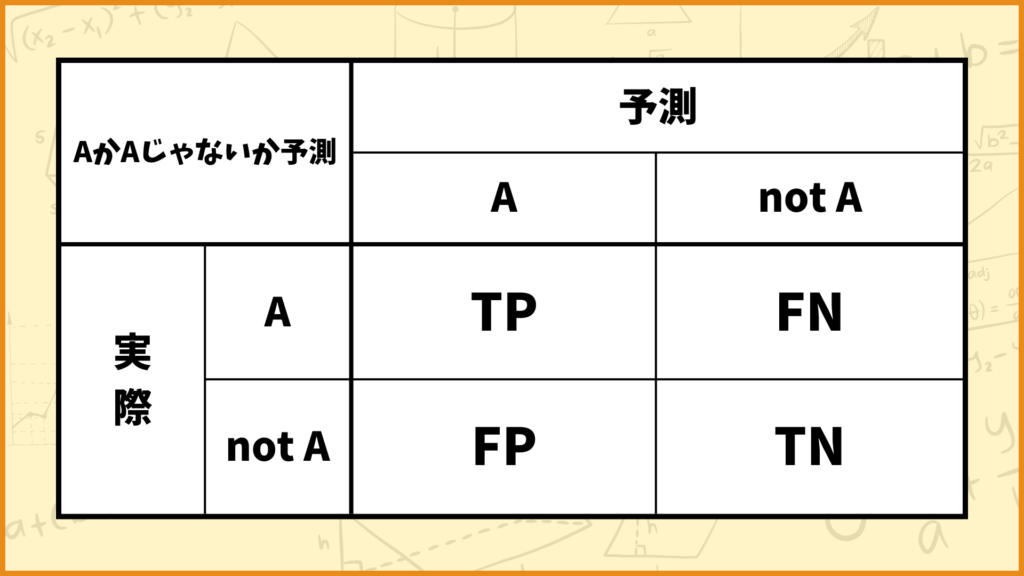
より一般的に説明します。与えらえたデータがAなのかそうでないのかの2値分類を考えます。このときのConfusion Matrixは上の表のようになります。ここでTP, FP, FN, TNとありますが、これらは
- TP (True Positive: 真陽性) : 実際に A で、モデルも正しく A と予測
- FP (False Positive: 偽陽性) : 実際は not Aなのに、モデルが誤って A と予測
- FN (False Negative: 偽陰性) : 実際は Aなのに、モデルが誤って not A と予測
- TN (True Negative: 真陰性) : 実際は not Aで、モデルも正しく not A と予測
を表しています。(なおAでないことはnot Aと表しています。)
例えば先ほどの犬か犬じゃないかを分類する例で考えます。Aが犬、not Aが犬じゃないとすると
- TP (True Positive: 真陽性) : 犬の画像で、モデルも正しく犬と予測
- FP (False Positive: 偽陽性) : 実際は犬じゃないなのに、モデルが誤って犬と予測
- FN (False Negative: 偽陰性) : 実際は犬なのに、モデルが誤って犬じゃないと予測
- TN (True Negative: 真陰性) : 実際は犬じゃなくで、モデルも正しく犬じゃないと予測
をそれぞれ表しています。これらTP, FP, FN, TNを使って次に説明するF1 scoreを計算していきます。
ちなみにTP,FP,FN,TNを使ってAccuracyを表すと
\(\text{Accuracy} = \frac{\text{TP}+\text{TN}}{\text{TP}+\text{FP}+\text{FN}+\text{TN}}\)
となります。分母は全データ数で、分子は正しくAと予測できた数と正しくAじゃないと予測できた数の和となります。
F1 scoreってなに?
F1 scoreを計算するためには、まずPrecisionとRecallを計算する必要があるので先にこれら2つについて説明し、最後にF1 scoreについて説明します。
Precisionってなに?
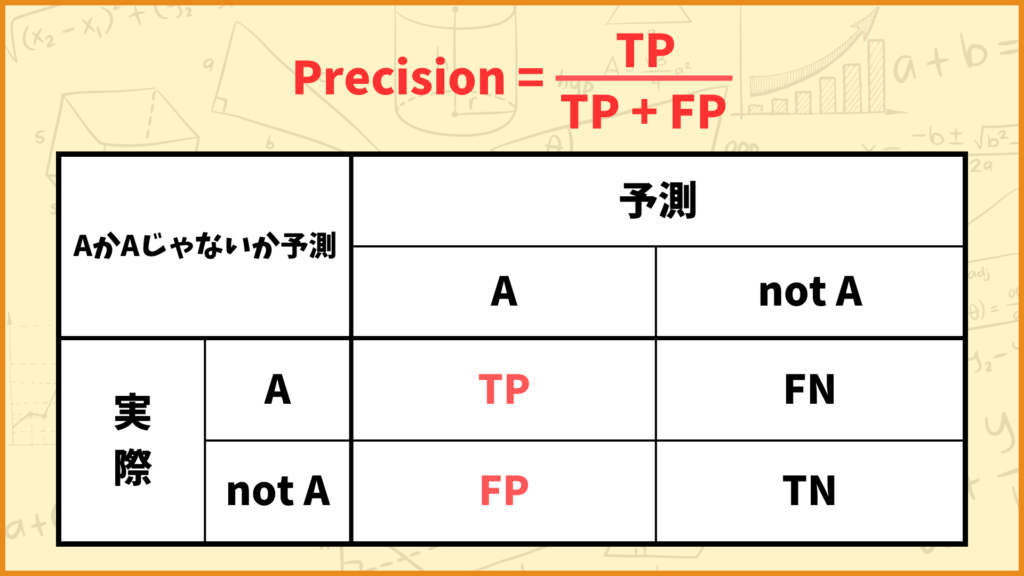
Precision(適合率)をザックリ説明すると
「モデルがAと予測したデータのうち、実際にAだったデータの割合」
です。Precisionの計算式は
\(\text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}}\)
となります。Precisionは0以上1以下の値を取り、値が大きいほど精度が良いと捉えることができます。
と言っても文字だけじゃ理解しづらいので具体例を使って詳しく見ていきましょう。
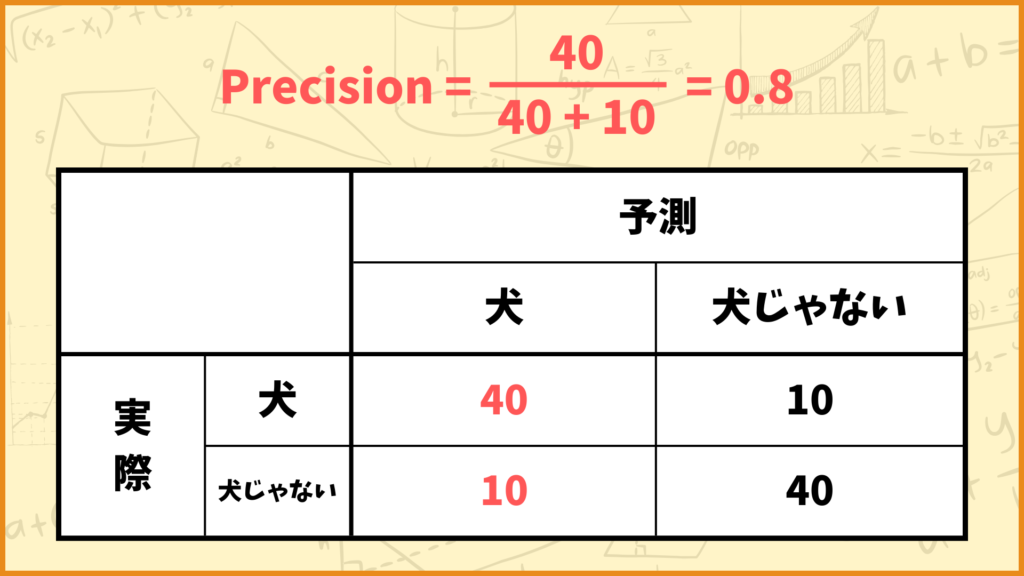
例えば上図のようなConfusion Matrixの場合、Precisionの値は
\(\text{Precision} = \frac{40}{40+10} = \frac{40}{50} = 0.8\)
と計算できます。つまりこれは
「モデルが犬と予測したデータのうち、80%が実際に犬の画像だった」
ということを表しています。
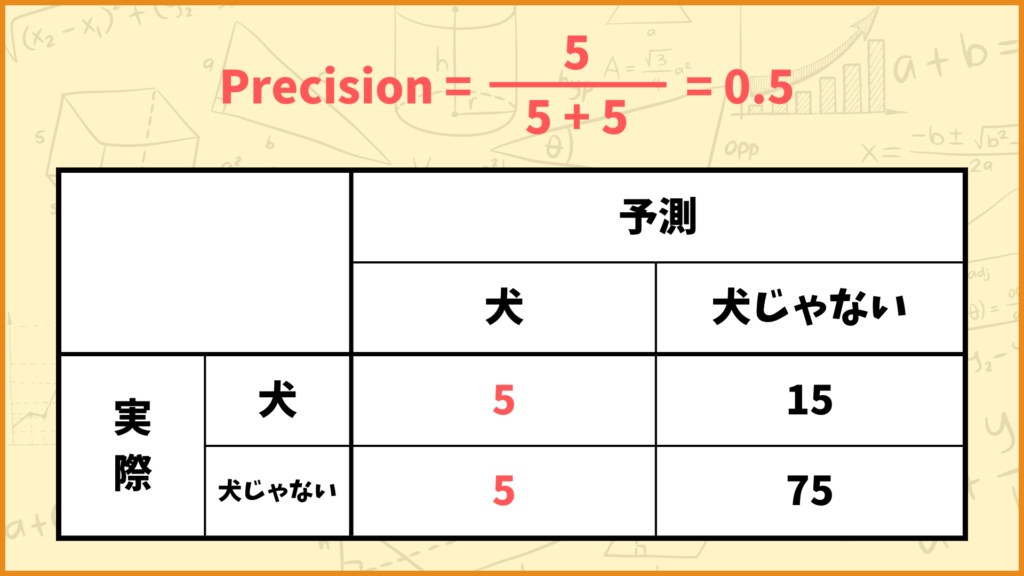
例えば上図のようなConfusion Matrixの場合、Precisionの値は
\(\text{Precision} = \frac{5}{5+5} = \frac{5}{10} = 0.5\)
と計算できます。つまりこれは
「モデルが犬と予測したデータのうち、50%が実際に犬の画像だった」
ということを表しています。
Recallってなに?
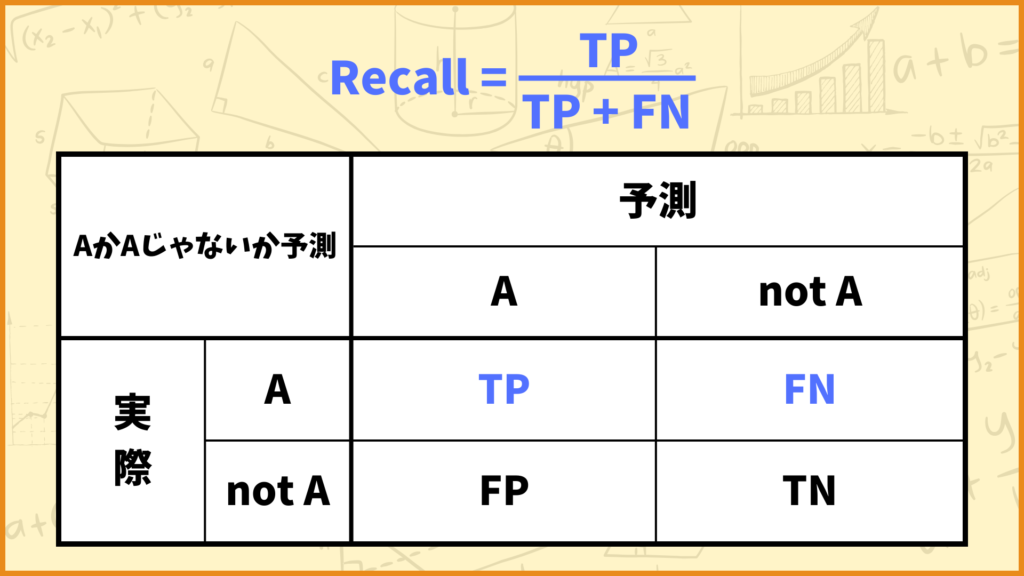
Recall(再現率)をザックリ説明すると
「実際にAであるデータのうち、モデルがAと予測したデータの割合」
です。Recallの計算式は
\(\text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}}\)
となります。Recallも0以上1以下の値を取り、値が大きいほど精度が良いと捉えることができます。
と言っても文字だけじゃ理解しづらいので具体例を使って詳しく見ていきましょう。
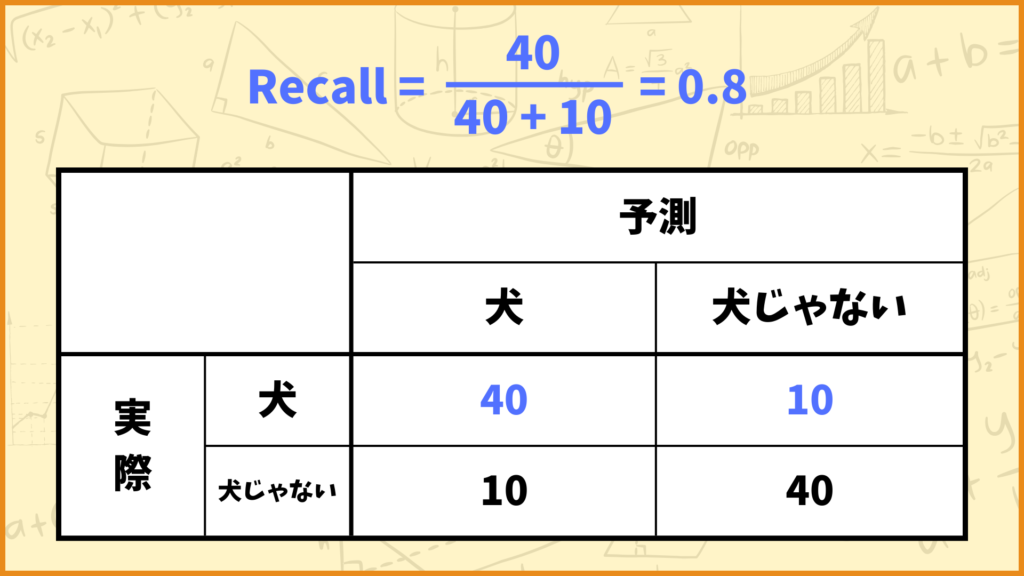
例えば上図のようなConfusion Matrixの場合、Recallの値は
\(\text{Recall} = \frac{40}{40+10} = \frac{40}{50} = 0.8\)
と計算できます。つまりこれは
「犬の画像のうち、モデルが犬と予測したのは80%だった」
と言うことを表しています。
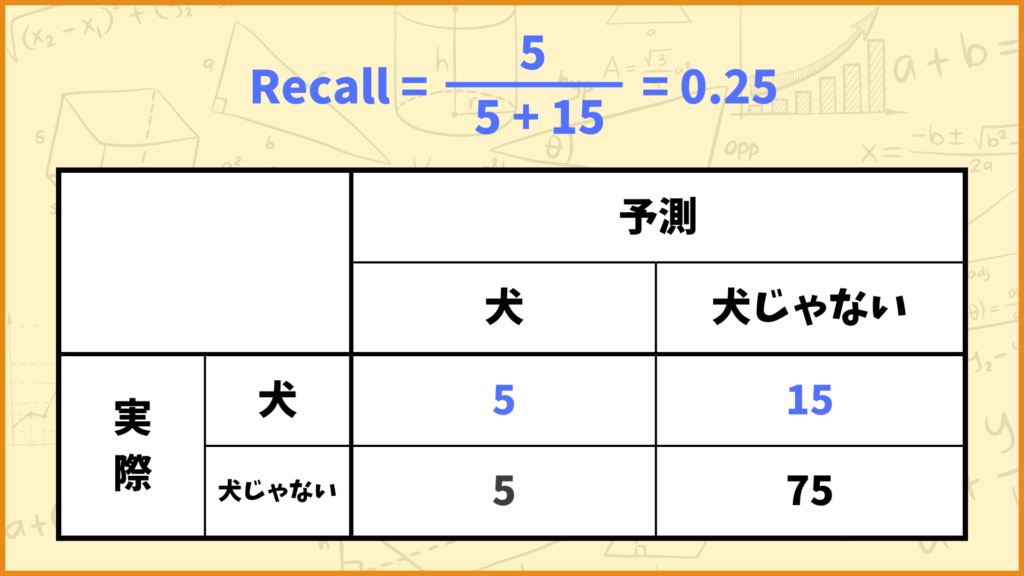
例えば上図のようなConfusion Matrixの場合、Recallの値は
\(\text{Recall} = \frac{5}{5+15} = \frac{5}{20} = 0.25\)
と計算できます。つまりこれは
「犬の画像のうち、モデルが犬と予測したのは25%だった」
ということを表しています。
極端な話どんな画像も犬と予測するモデルがある場合、Precisionの値は小さな値となりRecallの値は1となります。
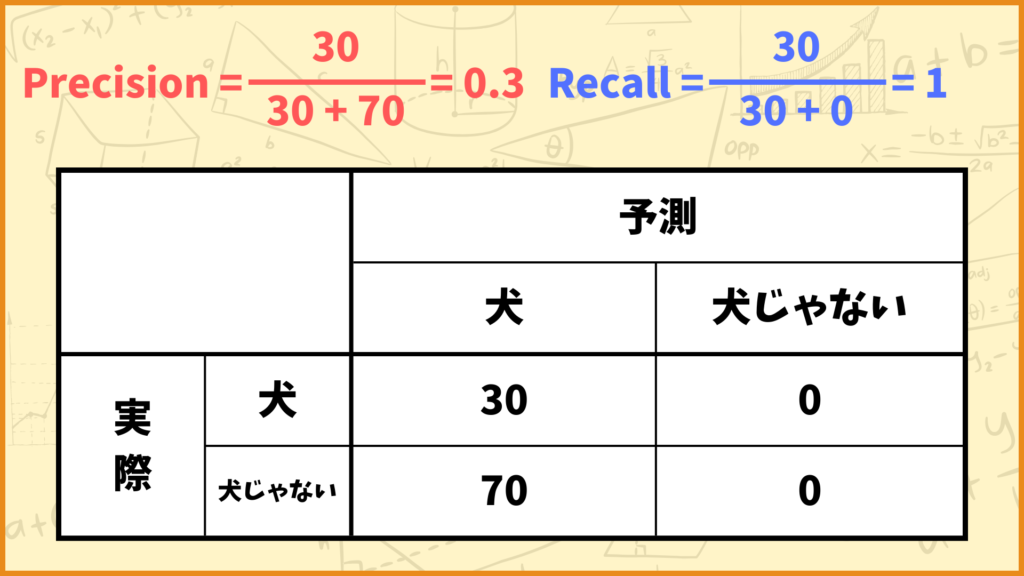
例えば犬の画像が30枚、犬じゃない画像が70枚だったとして、予測モデルが全ての画像を犬と判断した場合を考えます。
このときPrecisionとRecallはそれぞれ
\(\text{Precision} = \frac{30}{30+70} = 0.3\)
\(\text{Recall} = \frac{30}{30+0} = 1\)
と計算できます。これは
「犬の画像は100%犬だと予測できているけど、犬と予測した画像のうち30%しか本当に犬の画像じゃなかった」
ということを表しています。
F1 scoreってなに?
それでは最後にF1 scoreについて説明していきます。F1 scoreは
\(\text{F1 score} = 2\times\frac{\text{Preision}\times\text{Recall}}{\text{Precision}+\text{Recall}}\)
で計算できる、2値分類の精度を評価する指標です。F1 scoreも0以上1以下の値を取り、F1 scoreの値が大きいと精度良く分類ができているということになります。
もう少し詳しく説明すると、F1 scoreはPrecisionとRecallの調和平均です。
\(\frac{1}{\text{F1 score}} = \frac{1}{2} \times (\frac{1}{\text{Precision}}+\frac{1}{\text{Recall}}) = \frac{\text{Precision} + \text{Recall}}{2\times\text{Precision}\times\text{Recall}}\)
∴ \(\text{F1 score} =2\times\frac{\text{Preision}\times\text{Recall}}{\text{Precision}+\text{Recall}} \)
具体例を使って詳しく見ていきましょう。
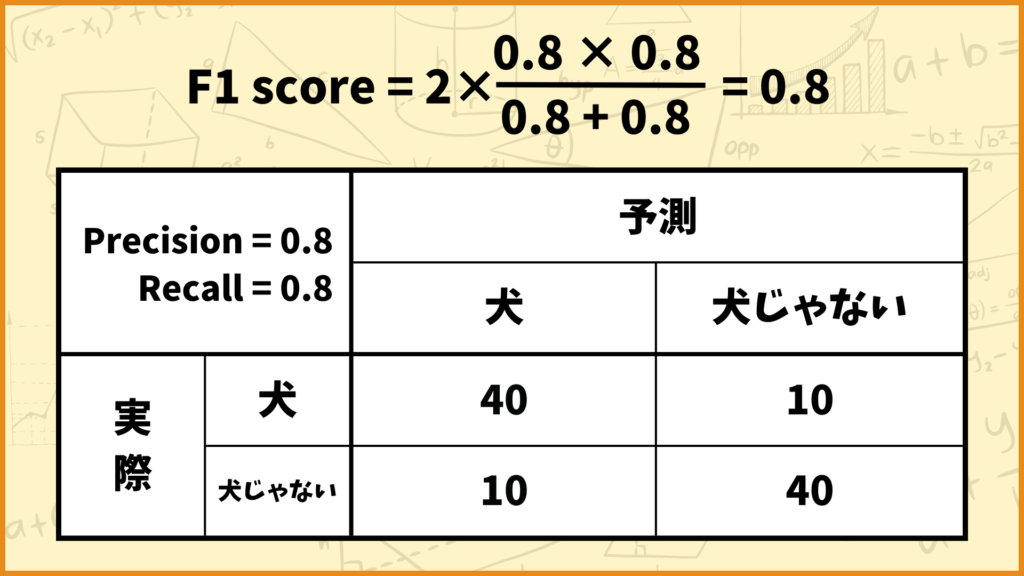
例えば上図のようなConfusion Matrixの場合、F1 scoreの値は
\(\text{F1 score} = 2\times \frac{\text{Precision} \times \text{Recall}}{\text{Precision}+\text{Recall}} = 2\times\frac{0.8\times0.8}{0.8+0.8} = 0.8\)
と計算できます。
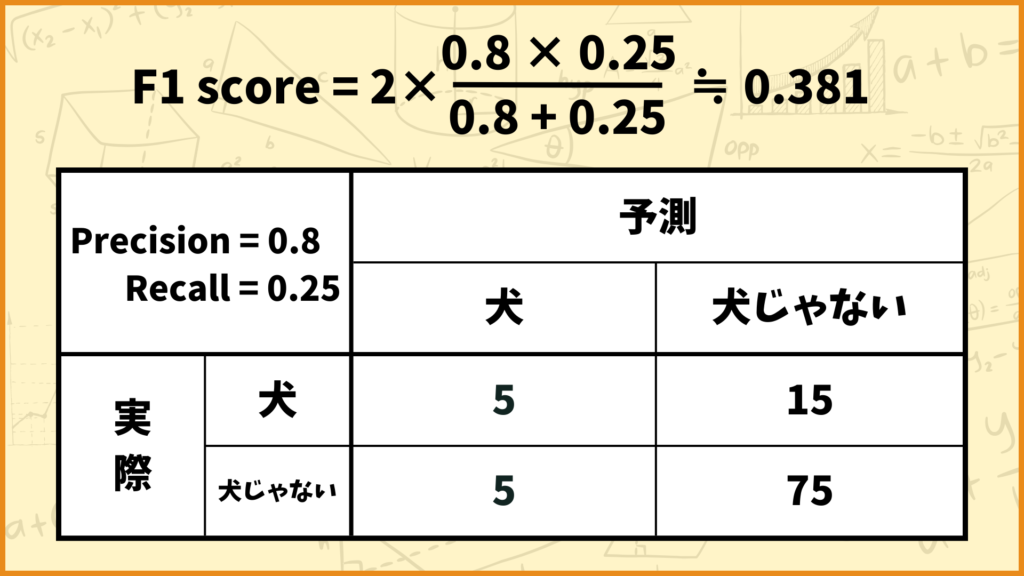
例えば上図のようなConfusion Matrixの場合、F1 scoreの値は
\(\text{F1 score} = 2\times \frac{\text{Precision} \times \text{Recall}}{\text{Precision}+\text{Recall}} = 2\times\frac{0.8\times0.25}{0.8+0.25} ≒ 0.381\)
と計算できます。
Accuracyは高いけどF1 scoreは低いときがある
ここまで2値分類における評価指標としてAccuracyやF1 scoreについて解説してきました。どちらもモデルがどれくらいの精度で分類できているかを表す指標ですが、データによってはAccuracyが高いけどF1 scoreは低いときがあるんです。
そのようなデータの1つの例として不均衡データが挙げられます。不均衡データとは、各クラスのデータ数が極端に偏っているデータのことです。

上図のような分類結果を考えてみましょう。このデータは犬の画像が20枚、犬じゃない画像が80枚の不均衡データです。このモデルでは犬の画像20枚中15枚、犬じゃない画像80枚中75枚を正しく分類することができています。
このときのAccuracyは0.8ですが、F1 scoreは0.381とAccuracyに比べて小さな値を取っています。このように不均衡データの時はAccuracyは高くてもF1 scoreは低い場合があるんです。
例えばネジの異常検知では、正常な画像に比べて異常があるネジの画像は極端に少ないはずです。そのような場合はAccuracyを考えるだけでは不十分で、F1 scoreなども用いる必要があります。
おわりに
いかがでしたか。
今回の記事ではAccuracy, F1 score, Confusion Matrixを解説しました。
今後もこのようなデータ分析に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。



