こんにちは！しゅんです！
この記事では有向グラフの隣接行列をn乗したときに各成分が何を表しているのかを解説しています。
隣接行列はグラフ理論で登場する用語で、グラフがどんな形をしているのかを知るのに重要な行列です。
それではやっていきましょう！
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください！
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます！
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学（けいえいこうがく、英: engineering management）は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
まず隣接行列を2乗して考えてみる
いきなり\(n\)乗を考えようとしても難しいのでまずは2乗について考えてみます。
具体例を使って考える
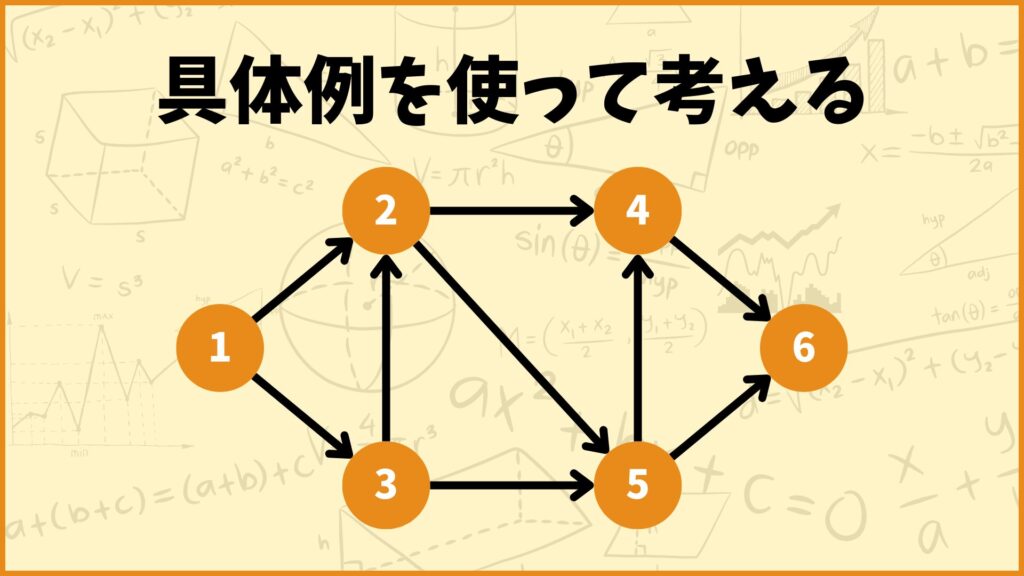
上の有向グラフを使って考えてみます。このグラフの隣接行列\(A\)は以下のように表せます。
\(A = \begin{pmatrix}0&1&1&0&0&0 \\ 0&0&0&1&1&0 \\ 0&1&0&0&1&0 \\ 0&0&0&0&0&1 \\ 0&0&0&1&0&1 \\ 0&0&0&0&0&0\end{pmatrix}\)
隣接行列の\((i,j)\)成分は辺\((i,j)\)があれば1、なければ0を取りますが、見方を変えると
「隣接行列の\((i,j)\)成分は頂点\(i\)から頂点\(j\)に1本の辺を使って到達できれば1、できなければ0を取る」
とも解釈することができます。このことを覚えておいてください。
隣接行列の求め方は以下の記事で詳しく解説しています！
現在制作中
次に\(A^2\)を計算してみましょう。
\(A^2 = \begin{pmatrix}0&1&1&0&0&0 \\ 0&0&0&1&1&0 \\ 0&1&0&0&1&0 \\ 0&0&0&0&0&1 \\ 0&0&0&1&0&1 \\ 0&0&0&0&0&0\end{pmatrix}\begin{pmatrix}0&1&1&0&0&0 \\ 0&0&0&1&1&0 \\ 0&1&0&0&1&0 \\ 0&0&0&0&0&1 \\ 0&0&0&1&0&1 \\ 0&0&0&0&0&0\end{pmatrix} = \begin{pmatrix}0&1&0&1&2&0 \\ 0&0&0&1&0&2 \\ 0&0&0&2&1&1 \\ 0&0&0&0&0&0 \\ 0&0&0&0&0&1 \\ 0&0&0&0&0&0\end{pmatrix}\)
それでは\(A^2\)と有向グラフ見比べてみましょう。
\(A^2\)
\(\begin{pmatrix}0&1&0&1&2&0 \\ 0&0&0&1&0&2 \\ 0&0&0&2&1&1 \\ 0&0&0&0&0&0 \\ 0&0&0&0&0&1 \\ 0&0&0&0&0&0\end{pmatrix}\)
例えば\(A^2\)の\((1,2)\)成分は1ですが、これは\(A\)の1行目と2列目を以下のように計算することで求められます。
\(\begin{pmatrix}0&1&1&0&0&0\end{pmatrix}\begin{pmatrix}1\\0\\1\\0\\0\\0\end{pmatrix}\)
\(=(0\times1)+(1\times0)+(1\times1)+(0\times0)+(0\times0)+(0\times0) = 1\)
この計算式を見ると、\(A^2\)の\((1,2)\)成分が1になっている理由は
「\(A\)の\((1,3)\)成分と\((3,2)\)成分が1」
であることが分かります。
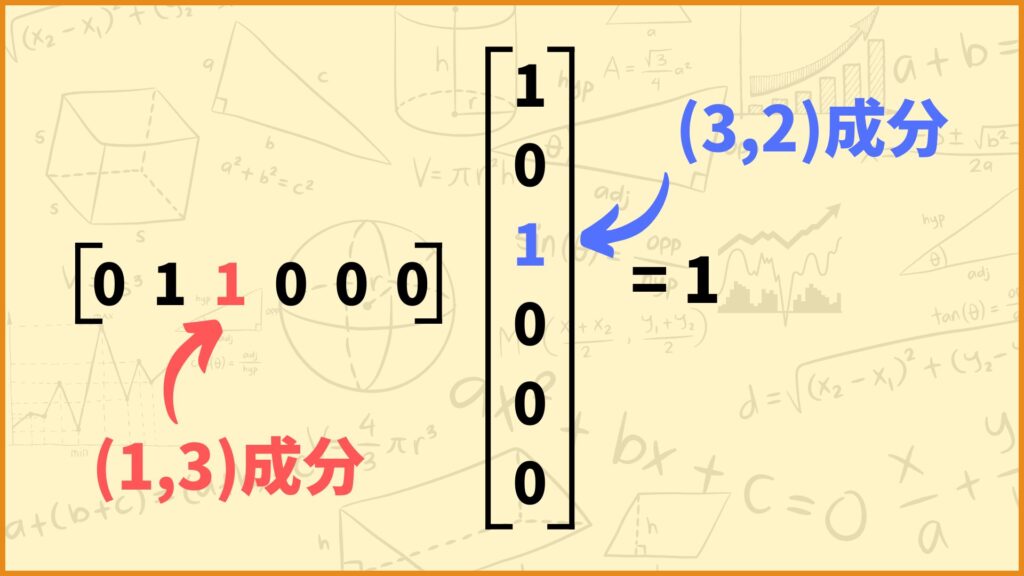
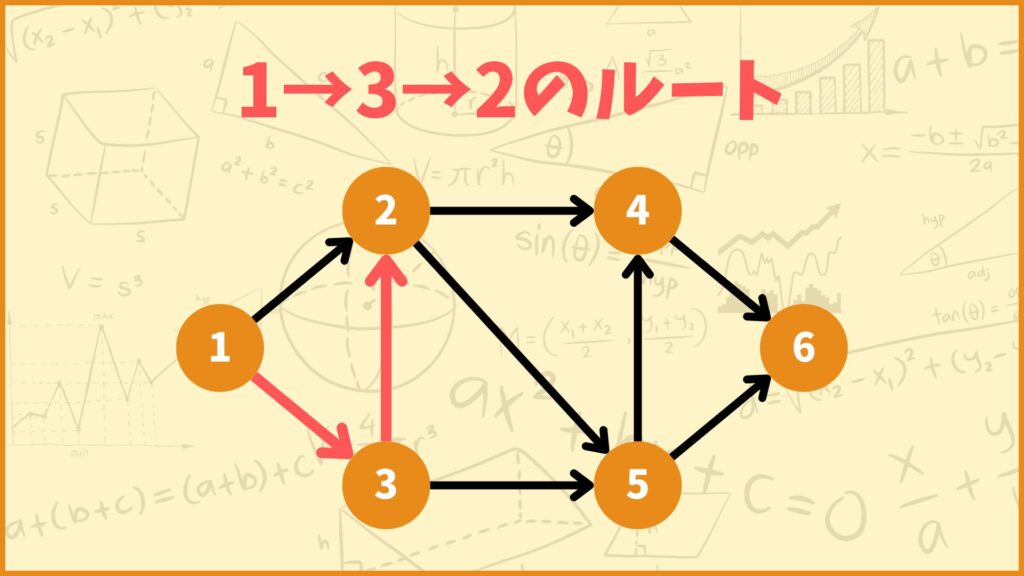
隣接行列\(A\)の\((1,3)\)成分は辺\((1,3)\)を表し、\((3,2)\)成分は辺\((3,2)\)を表すので、「\(A\)の\((1,3)\)成分と\((3,2)\)成分が1」ということは頂点1→頂点3→頂点2のルートが存在することを表しています。つまり\(A^2\)の\((1,2)\)成分は
「頂点1から頂点2へ2本の辺を使って到達できるルートが1つある」
ということを表しています。
他にも見てみましょう。\(A^2\)の\((2,6)\)成分は2ですが、これは\(A\)の2行目と6行目を以下のように計算することで求めまられます。
\(\begin{pmatrix}0&0&0&1&1&0\end{pmatrix}\begin{pmatrix}0\\0\\0\\1\\1\\0\end{pmatrix}\)
\(=(0\times0)+(0\times0)+(0\times0)+(1\times1)+(1\times1)+(0\times0) = 2\)
この計算式を見ると、\(A^2\)の\((2,6)\)成分が2になっている理由は
「\(A\)の\((2,4)\)成分と\((4,6)\)成分が1」
「\(A\)の\((2,5)\)成分と\((5,6)\)成分が1」
であることが分かります。隣接行列\(A\)の\((2,4)\)成分は辺\((2,4)\)を表し、\((4,6)\)成分は辺\((4,6)\)を表します。また隣接行列\(A\)の\((2,5)\)成分は辺\((2,5)\)を表し、\((5,6)\)成分は辺\((5,6)\)を表します。
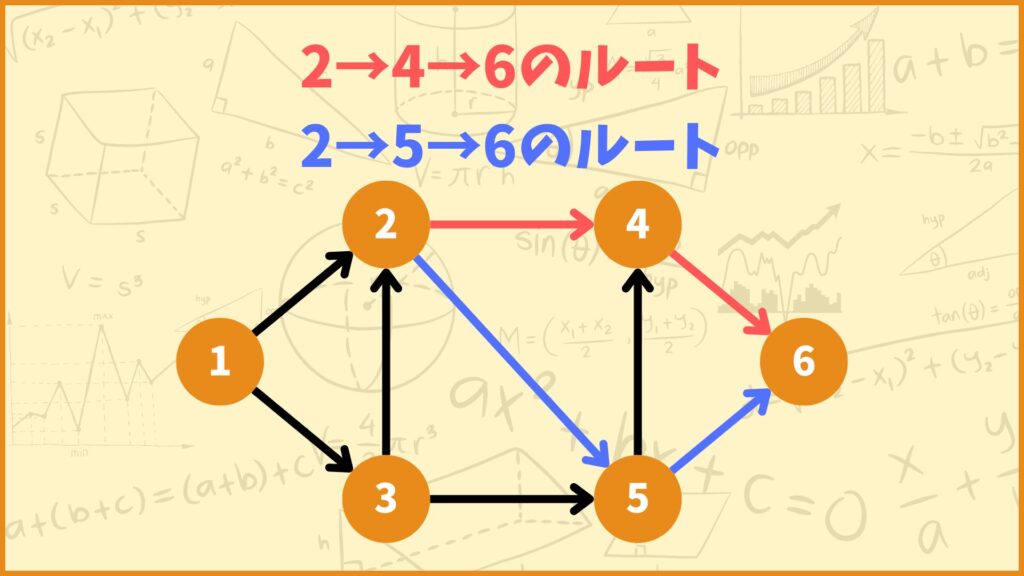
したがって「\(A\)の\((2,4)\)成分と\((4,6)\)成分が1」ということは頂点2→頂点4→頂点6のルートが存在することを表しています。また「\(A\)の\((2,5)\)成分と\((5,6)\)成分が1」ということは頂点2→頂点5→頂点6のルートが存在することを表しています。つまり\(A^2\)の\((2,6)\)成分は
「頂点2から頂点6へ2本の辺を使って到達できるルートが2つある」
ということを表しています。
より一般的に考えてみる
結論：
有向グラフ\(G = (V,E)\)の隣接行列を\(A\)とし、\(A^2\)の\((i,j)\)成分を\(a_{ij}^{(2)}\)とする。このとき\(a_{ij}^{(2)}\)は、頂点\(i\)から頂点\(j\)に2つの辺を使って到達できるルートの本数を表す。
それではより一般的に考えてみましょう。結論上記のことが成り立ちます。頂点数\(m\)の有向グラフ\(G = (V,E)\)の隣接行列を\(A\)とし、\(A\)の\((i,j)\)成分を\(a_{ij}^{(1)}\)とします。また\(A^2\)の\((i,j)\)成分を\(a_{ij}^{(2)}\)とします。このとき
\(a_{ij}^{(2)} = \sum\limits_{k=1}^{m}a_{ik}^{(1)}a_{kj}^{(1)}\)
という式が成立します。（行列の積の定義に従えば上記の式が得られます。）
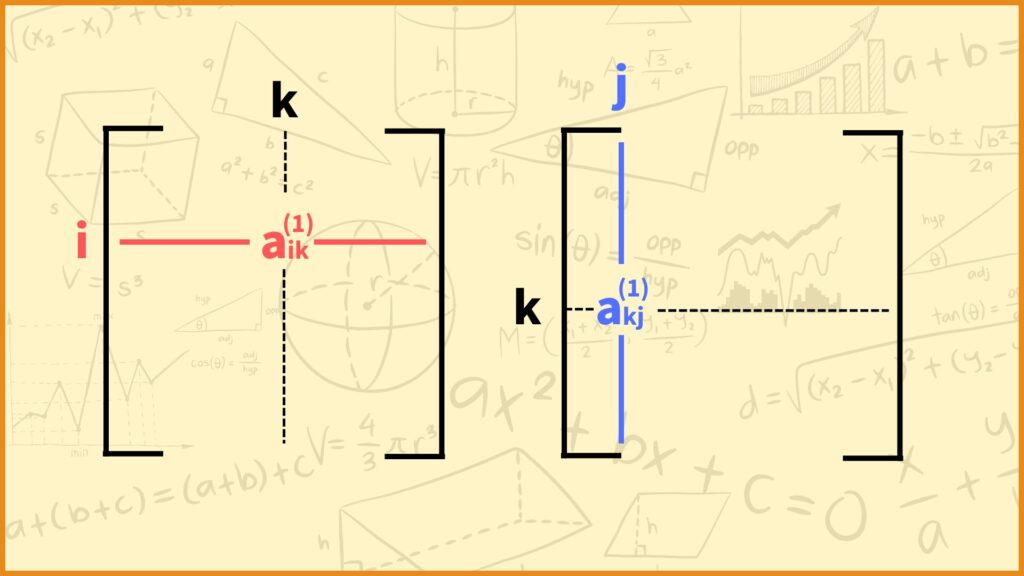
\(A\)の各成分は0か1しか取らないので\(a_{ij}^{(2)}\)の値は\(a_{ik}^{(1)}=a_{jk}^{(1)}=1\)を満たす頂点\(k\)の数と一致します。では\(a_{ik}^{(1)}=a_{jk}^{(1)}=1\)を満たす頂点\(k\)がどんな頂点なのかを考えてみましょう。
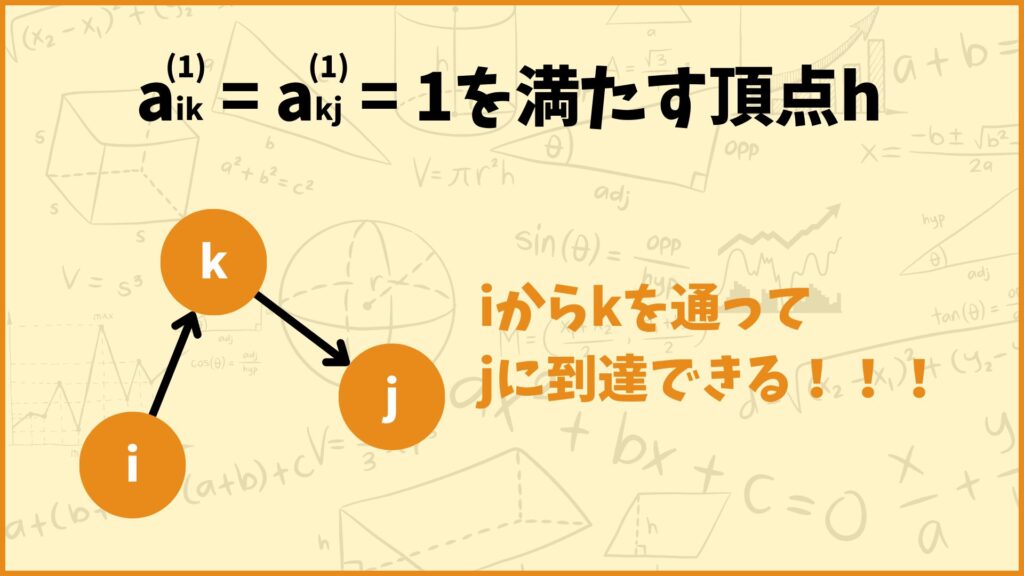
\(a_{ik}^{(1)}=1\)は辺\((i,k)\)があるということを示します。また\(a_{kj}^{(1)}=1\)は辺\((k,j)\)があるということを示しています。よって\(a_{ik}^{(1)}=a_{jk}^{(1)}=1\)は頂点\(i\)から頂点\(k\)を通って頂点\(j\)に到達することができるということを表しています。
このとき\(i\)から\(j\)に到達するためのルートは必ず2つの辺を使っていることが分かります。また\(\sum\limits_{k=1}^{m}a_{ik}^{(1)}a_{kj}^{(1)}\)はグラフ中の全ての頂点\(k\)に対して上記の計算を行っています。
以上のことから隣接行列の2乗\(A^2\)の\((i,j)\)成分\(a_{ij}^{(2)}\)は
「頂点\(i\)から頂点\(j\)へ2つの辺を使って到達できるルートの本数」
を表しています。
結論：
有向グラフ\(G = (V,E)\)の隣接行列を\(A\)とし、\(A^2\)の\((i,j)\)成分を\(a_{ij}^{(2)}\)とする。このとき\(a_{ij}^{(2)}\)は、頂点\(i\)から頂点\(j\)に2つの辺を使って到達できるルートの本数を表す。
隣接行列をn乗してみる
結論：
有向グラフ\(G = (V,E)\)の隣接行列を\(A\)とし、\(A^n\)の\((i,j)\)成分を\(a_{ij}^{(n)}\)とする。このとき\(a_{ij}^{(n)}\)は、頂点\(i\)から頂点\(j\)に\(n\)本の辺を使って到達できるルートの本数を表す。
結論上記のことが成り立ちます。これを帰納法を使って証明します。考え方は隣接行列を2乗したときと同じです。まず\(n = 1\)のときを考えます。とは言ってもこれは隣接行列\(A\)の定義から上記が成り立つのは明らかですね。
次に\(n = t\)のときに上記のことが成り立つと仮定して、\(n = t+1\)のときについて考えてみます。隣接行列\(A\)の\((t+1)\)乗\(A^{t+1}\)は以下のように表せます。
\(A^{t+1} = A^{t}A\)
よって\(A^{t+1}\)の\((i,j)\)成分は以下のように表せます。（行列の積の定義に従えばすぐに分かります。またグラフの頂点数は\(m\)とします。）
\(a_{ij}^{(t+1)} = \sum\limits_{k = 1}^{m}a_{ik}^{(t)}a_{kj}^{(1)}\)
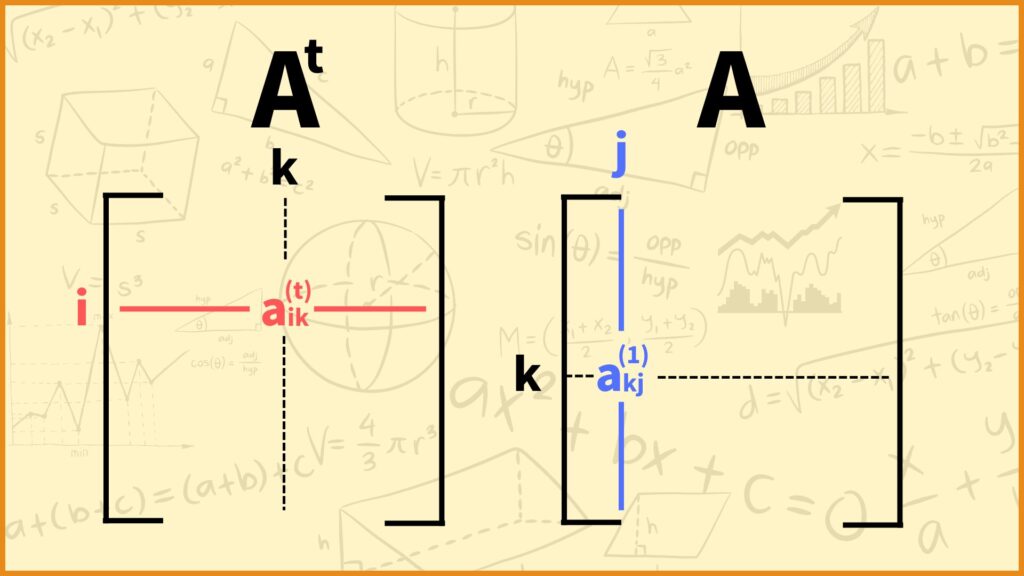
ここで帰納法の仮定から\(a_{ik}^{(t)}\)は頂点\(i\)から頂点\(k\)に\(t\)本の辺を使って到達できるルートの本数を表しています。\(a_{kj}^{(1)}\)は辺\((k,j)\)があれば1、なければ0を取るので、\(a_{ik}^{(t)}a_{kj}^{(1)}\)は頂点\(i\)から頂点\(k\)を通って頂点\(j\)に\(t+1\)本の辺を使って到達できるルートの本数を表しています。
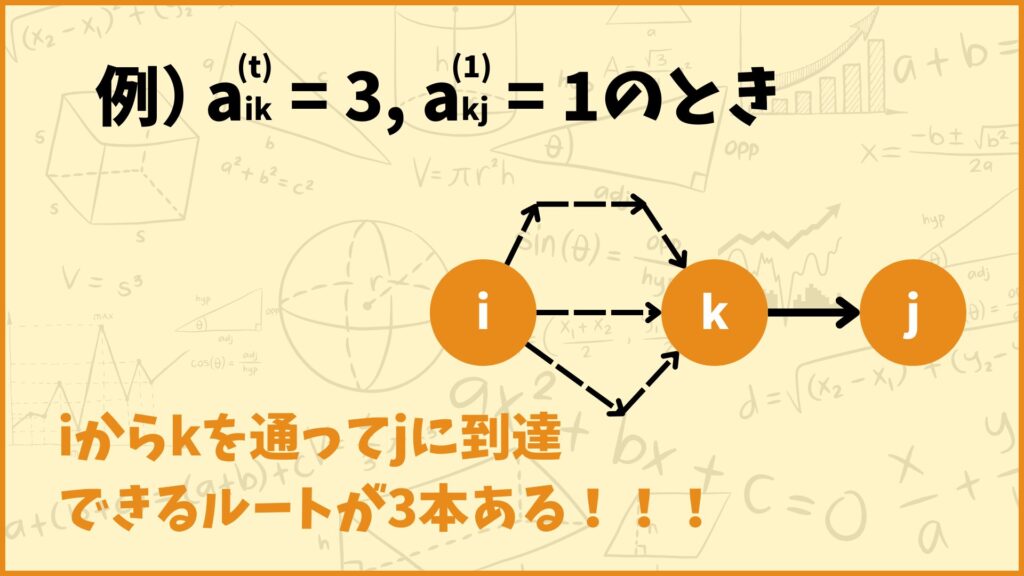
\(\sum\limits_{k = 1}^{m}a_{ik}^{(t)}a_{kj}^{(1)}\)はこの計算をグラフ中の全ての頂点\(k\)に対して行っています。
以上のことから隣接行列の\(n\)乗\(A^n\)の\((i,j)\)成分\(a_{ij}^{(n)}\)は
「頂点\(i\)から頂点\(j\)へ\(n\)本の辺を使って到達できるルートの本数」
を表しています。
結論：
有向グラフ\(G = (V,E)\)の隣接行列を\(A\)とし、\(A^n\)の\((i,j)\)成分を\(a_{ij}^{(n)}\)とする。このとき\(a_{ij}^{(n)}\)は、頂点\(i\)から頂点\(j\)に\(n\)本の辺を使って到達できるルートの本数を表す。
おわりに
いかがでしたか。
今回の記事では隣接行列について解説していきました。
今後もこのようなグラフ理論に関する記事を書いていきます！
最後までこの記事を読んでくれてありがとうございました。
