こんにちは!しゅんです!
今回の記事は2部グラフの最小重み完全マッチングついて解説していきます!
マッチングとはグラフ理論という数学の分野で登場する用語で、現実世界の様々な分野で応用できます。
マッチングには色々な種類がありますが、その中でも今回は2部グラフの最小重み完全マッチングがどんなものなのか解説したいと思います!
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
2部グラフってなに?
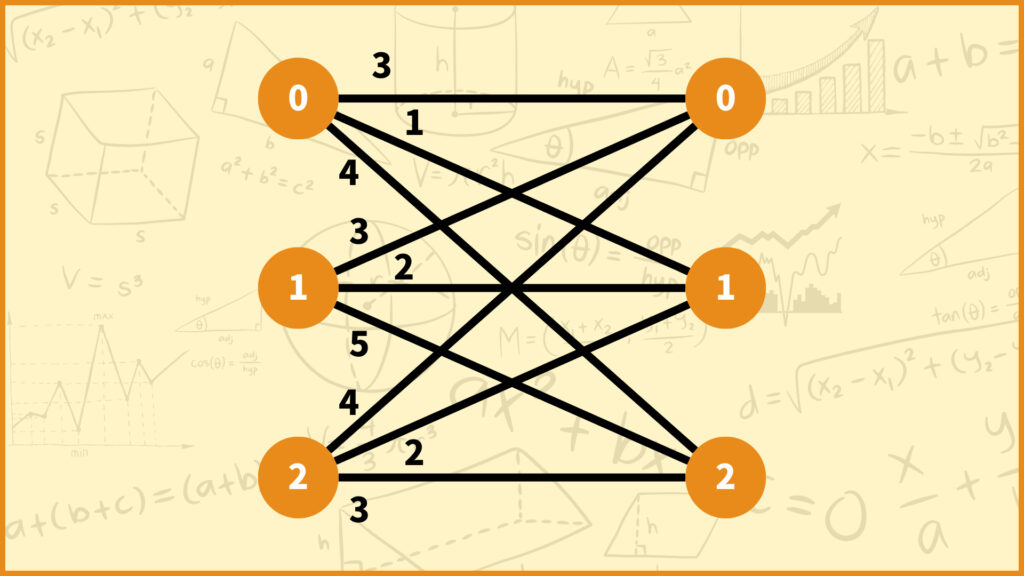
まず最初に2部グラフがどんなグラフなのかを説明したいと思います。2部グラフとは上図のように頂点が2つのグループに分かれているグラフのことを指します。
ちゃんと定義すると2部グラフ\(G=(V,E)\)とは以下の2つの性質を満たすグラフのことです。
1. 頂点集合\(V\)が2つの部分集合\(V_1,V_2\)に分割される。
2. 各部分集合\(V_1,V_2\)内の頂点間には辺が存在しない。
その中でも上図の2部グラフに関して左側のある頂点に着目してみると、その頂点と右側の全ての頂点との間に辺がありますね。また右側のある頂点に着目してみても、その頂点と左側の全ての頂点との間に辺がありますね。
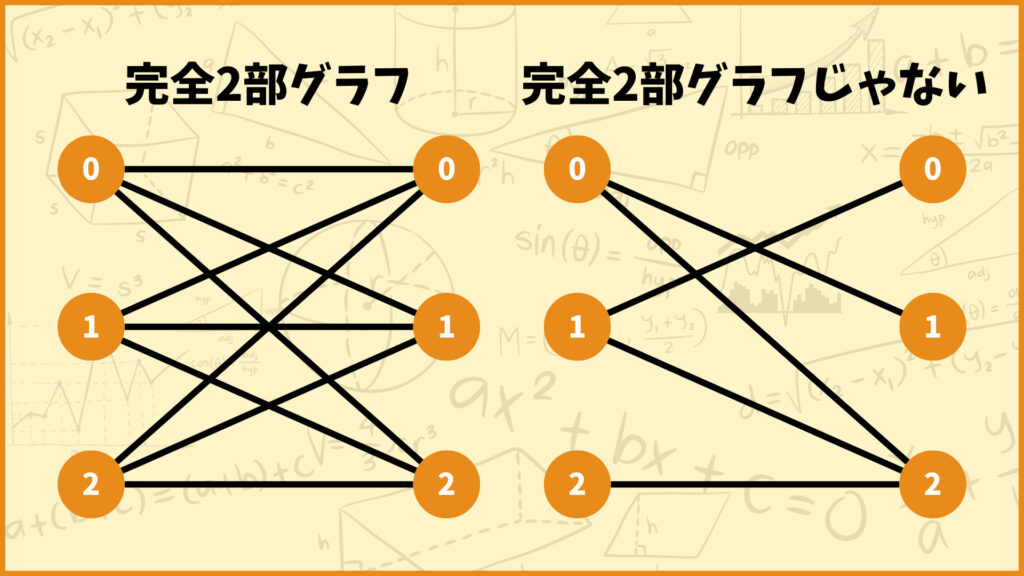
このような2部グラフを完全2部グラフと言います。
最小重み完全マッチングってなに?
それでは次に最小重み完全マッチングについて説明したいと思います。
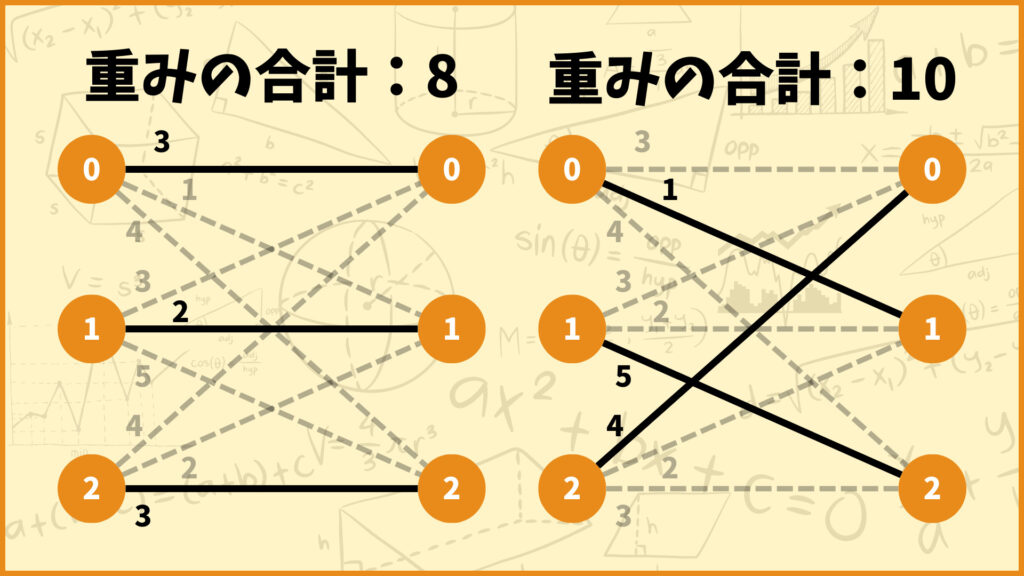
上の二つの完全マッチングについて考えてみましょう。マッチングの図の上に「重みの合計」と書いてありますが、これはマッチングとして採用された辺の重みを合計したものです。
完全マッチングについてはこちらの記事で解説しています!
現在制作中
例えば左のマッチングの重みの合計は3+2+3=8で、右のマッチングの重みの合計は1+5+4=10となります。
そして最小重み完全マッチングとは、この「重みの合計」が最も小さいマッチングのことを表します。
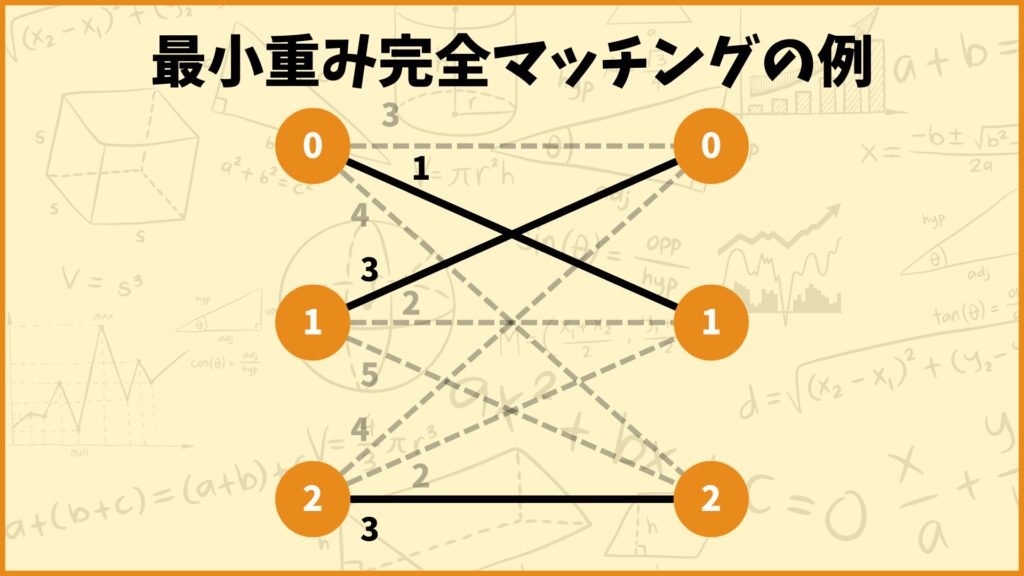
上図の完全マッチングは重みの合計が7で、実はこれが最小重み完全マッチングになります。次回の記事ではこの「2部グラフの最小重み完全マッチング」を整数計画問題として定式化する方法を解説したいと思います!
2部グラフの最小重み完全マッチングを整数計画問題として定式化する方法はこちらの記事で解説しています!
現在制作中
おわりに
いかがでしたか。
今回の記事では2部グラフの最小重み完全マッチングについて解説していきました。
今後もこのようなグラフ理論に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。