こんにちは!しゅんです!
最近NBA界隈で話題になっているコーギーの動画があるんですよね。その動画はコーギーがNBAプレーオフの試合を予想すると言うもので、この的中率がすごいんです。
プレーオフの西2回戦で行われたゴールデンステイト・ウォリアーズvsロサンゼルス・レイカーズの試合を、なんとこのコーギーが7試合中6試合も勝敗予想を的中させたんです!
(気になる人は調べてみたら動画が出てくると思います。)
ということで今回はこの的中精度は果たして偶然ではないのかを仮説検定で確かめていこうと思います!
それでは解説していきましょう!
統計検定2級に関する記事はこちらから見れます!
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
6試合も的中させるのってどれくらいすごいの?
まずは7試合中6試合も的中させるのがどれくらいの確率なのかを計算してみましょう。もし予想が的中する確率が\(\frac{1}{2}\)だとすると、この予想は\(n=7, \; p=\frac{1}{2}\)の二項分布に従っていると考えられます。
二項分布はこちらの記事で詳しく解説しています!
このことを利用すると7試合中6試合の予想を的中させる確率は以下の式で表せます。
\( _7 C_6 × (\frac{1}{2})^7\)
\(=0.0546875\)
ということで7試合中6試合的中させる確率は約5.5%だということが分かりました。これだけ見ると偶然とは言い難い現象ですね。コーギーは本当に予言していたのでしょうか。
仮説検定ってなに?
簡単に説明すると仮説検定とはある仮説が正しいかどうかを確かめることです。例えばコイントスを考えてみましょう。
あるコインはおもてとうらがどちらも\(\frac{1}{2}\)の確率で出ると言われています。しかしそのコインを100回投げたらおもてが90回出ました。
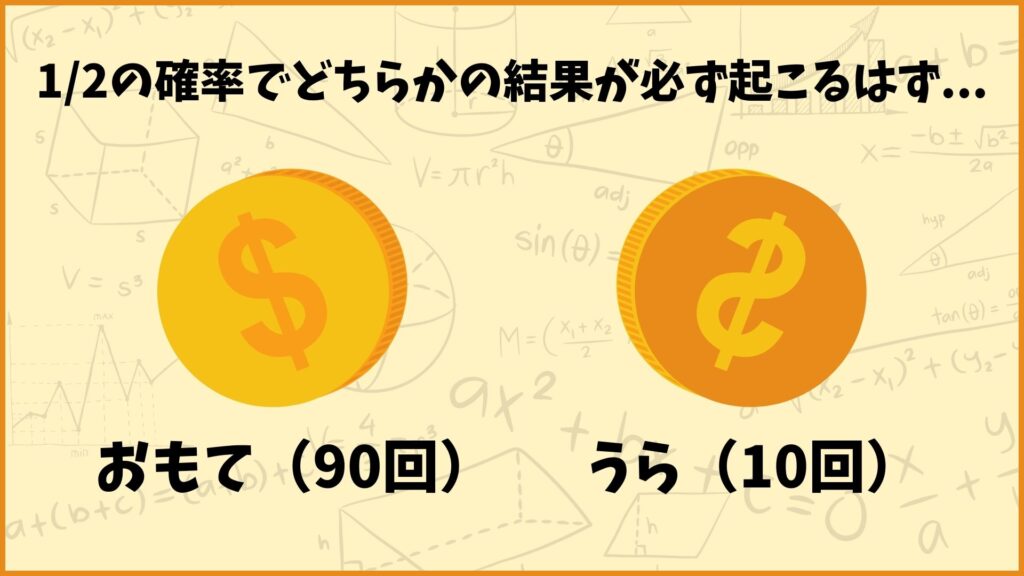
果たしてこのとき本当に「そのコインはおもてもうらも\(\frac{1}{2}\)の確率で出る」という仮説は正しいのでしょうか。ぱっと見正しくなさそうに見えますよね。
このことをちゃんと検証する方法が仮説検定です。統計で非常によく使われますね。
仮説検定を行う
それでは実際に仮説検定を行ってコーギーに予言能力があるという仮説を検証してみましょう。
帰無仮説と対立仮説
仮説検定を行う前にまず問題設定を行いましょう。検定をするためには帰無仮説と対立仮説と言うものが必要です。
帰無仮説とは何かが「ない」ことを表す仮説で、今回の場合だと「コーギーには予言能力はない」という仮説になります。この記事では帰無仮説のことを\(H_0\)と表します。
一方で対立仮説とはその逆の仮説で、今回の場合だと「コーギーには予言能力がある」という仮説になります。この記事では対立仮説のことを\(H_1\)と表します。
一般的には何か違いや差があるって言いたいときは対立仮説で主張しその反対として帰無仮説で違いや差がないと主張します。
仮説検定では帰無仮説が正しくない or 正しくないとは言えないかを判断します。今回の場合だと「コーギーには予言能力がある」or「コーギーには予言能力があるとは言えない」かを判断していきます。
検定に用いる評価範囲
例えば勝敗を的中させた回数を\(x\)とすると、検定をするときに\(x=6\)の確率だけを考えれば良いというわけではありません。なぜなら6回的中させるよりも7回的中させる方が珍しいからです。
今回は6回的中させることが珍しいかどうか考えていますが、6回が珍しいなら7回はもっと珍しいですよね。仮説検定では6回的中させることが珍しいかどうかを考えるのではなく、6回以上的中させることが珍しいかどうかで考えます。
さらに言うと、今回の場合6回的中させることと1回的中させることは実質的には同じです。1回勝つチームを的中させたということは、言い換えると6回負けるチームを的中させたということになります。同じように考えると0回的中させることは7回的中させることと実質的には同じです。
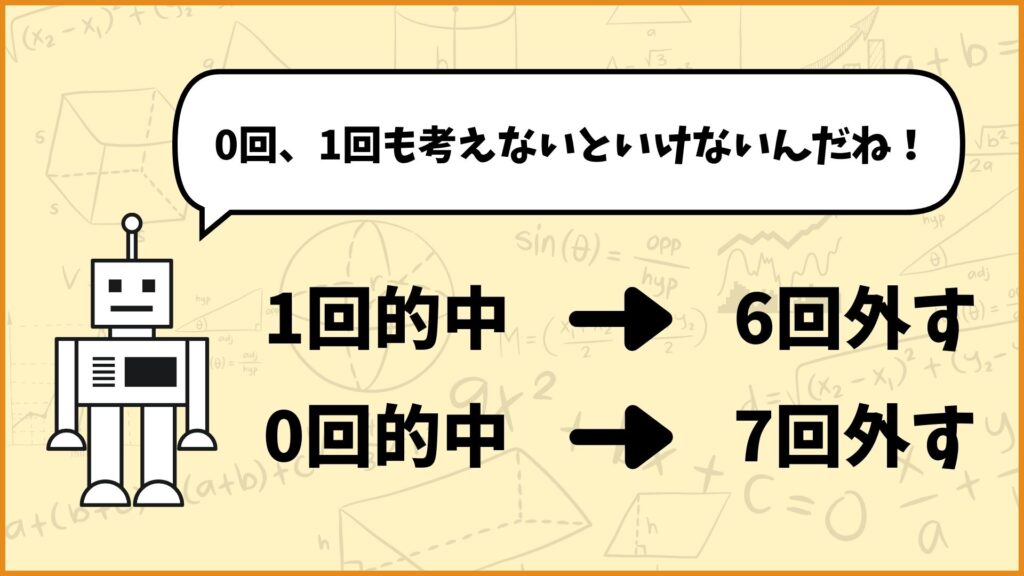
以上のことから仮説検定に用いる評価範囲は\(x=0,1,6,7\)の4つになります。ではこのことを式で表すにはどうすれば良いでしょうか。
ポイントは期待値です。期待値からどれくらい離れているかを考えることで評価範囲を式で表すことができます。簡単に言うと、6回的中や0回的中というような現象がなぜ珍しいかというとそれは二項分布における期待値(平均値)から大きく離れているからです。
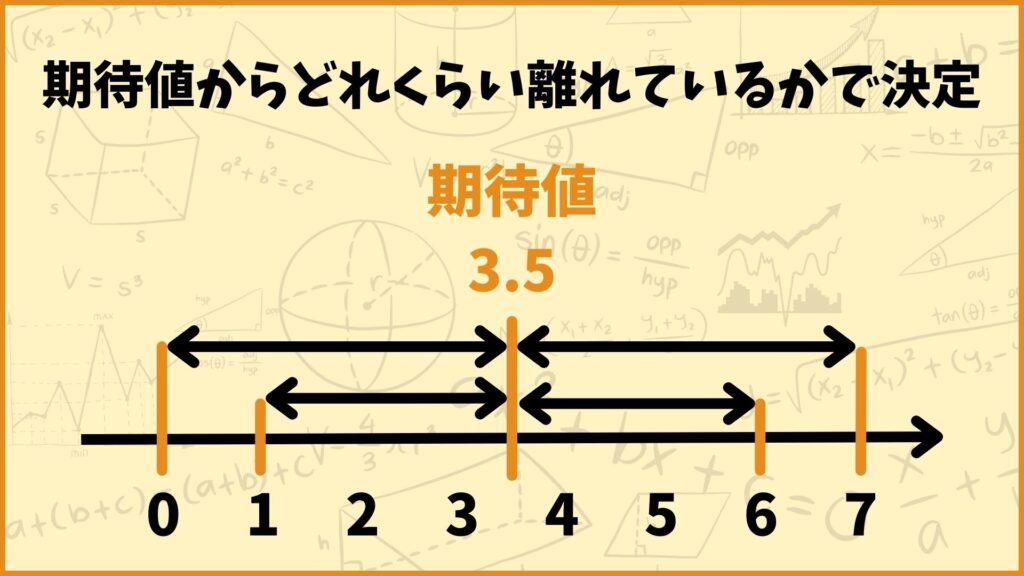
二項分布の期待値は\(np=3.5\)なので6までの距離は2.5となります。つまり期待値までの距離が2.5以上となるようなものだけ選ぶという表記にすれば良いです。
以上のことをまとめると、的中させた試合数を\(x\)、期待値を\(\mu\)としたときに検定で用いる範囲は下のようになります。
\(|x-\mu|\geq2.5\)
\(H_0\)という仮定の下でこの範囲を満たすような確率を数式で表すときは下のようになります。
\(P(|x-\mu|\geq2.5 \; | \; H_0)\)
長々と説明してきましたが、これで今回求めたい確率を数式で表記することができました。ぶっちゃけ確率を計算するだけならこんなめんどくさい数式表記をせずにただ\(x=0,1,6,7\)の確率を足せば良いのですが、厳密に表すとこんな感じになります。
少し難しい話になりますが今回は両側検定を用いています。
どれくらい珍しいか確率を求めてみる
それでは実際にコーギーが行った予想がどれくらい珍しいのか確率を求めてみましょう。先ほど数式で表した
\(P(|x-\mu|\geq2.5 \; | \; H_0)\)
この式の値を求めればよいです。この式は\(H_0\)の仮定(コーギーには予言能力がない)のもと、的中回数から期待値(3.5)を引いた値が2.5以上になるようなものだけを取り出して確率を求めて足してくださいということを表しています。
これをみたすのは\(x=0,1,6,7\)のときなので、的中回数が0回、1回、6回、7回の確率を求めて足し算しましょう。
先ほど説明したように今回の予想は二項分布を使って表すことができるので当てはめてみましょう。
\( _7 C_0 × (\frac{1}{2})^7\)
\(=0.0078125\)
\( _7 C_1 × (\frac{1}{2})^7\)
\(=0.0546875\)
\( _7 C_6 × (\frac{1}{2})^7\)
\(=0.0546875\)
\( _7 C_7 × (\frac{1}{2})^7\)
\(=0.0078125\)
ということで各回数の確率が計算で来たので全部足しましょう。
\(P(|x-\mu|\geq2.5 \; | \; H_0)=0.125\)
というわけで0.125という確率で今回のコーギーのようなことが起こるということが分かりました。果たしてこの確率は「コーギーには予言能力がある」と判断できるのでしょうか。
有意水準\(\alpha\)ってなに?
この判断をするために有意水準\(\alpha\)というものを使います。ザックリ説明すると有意水準とはどれくらいの確率だったら帰無仮説が間違っていると言えるかの基準のことです。
例えば有意水準が0.5だったら、確率が50%以下だったとき帰無仮説が正しくない、すなわちコーギーには予言能力があると言えます。
統計の世界では有意水準として0.05が使われることが多いです。
場合によっては有意水準として10%(\(\alpha=0.1\))や1%(\(\alpha=0.01\))が使われることもあります。
コーギーに予言能力があるとは言えない
有意水準5%で考えてみましょう。今回求めた確率は12.5%で有意水準を大きく超えていますね。そのためこの確率はそれほど珍しくはないと判断することができます。
すなわち今回の仮説検定ではコーギーの予想はそれほど珍しいとは言えず、「コーギーには予言能力がある」とは言えませんでした。

このように有意水準をより確率が大きい場合は「有意水準5%では帰無仮説\(H_0\)が棄却されない」と言います。逆に有意水準より確率が小さい場合、例えば確率が0.03だった場合は「有意水準5%で帰無仮説は棄却される」と言います。
おわりに
いかがでしたか。
今回の記事ではNBA界隈で話題になっているコーギーに予言能力があるのかについて仮説検定を用いて解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。