こんにちは!しゅんです!
今回の記事はpythonでグラフの離心数を計算する方法について解説していきます!
前回の記事では離心数・半径・直径・中心がどんなものか、どうやって計算するのかを説明しました。でもグラフが大きくなってくると自分で計算するのは難しくなってきます。
そんなときにはコンピュータに計算してもらうのが手っ取り早いです。ということで今回はpythonでグラフの離心数を計算していきたいと思います!
それではやっていきましょう!
\\\ 前回の記事はこちら! ///
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
pythonでグラフの離心数を計算するコード
以下のコードで離心数を計算することができます。
## 事前準備
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
## グラフを作成する
# 空の無向グラフを作成
G = nx.Graph()
# 頂点データの追加
G.add_nodes_from(["A","B","C","D","E","F","G","H","I","J","K","L","M"])
# 辺データの追加
G.add_edges_from([("A","D"),("D","L"),("L","M"),("M","J"),("J","B"),("B","A"),
("C","F"),("F","I"),("I","K"),("K","H"),("H","E"),("E","C"),
("A","C"),("D","F"),("L","I"),("M","K"),("J","H"),("B","E"),
("C","G"),("F","G"),("I","G"),("K","G"),("H","G"),("E","G"),])
# 頂点の座標を設定する
pos = {
"A": (1,5),
"B": (3,3),
"C": (3,5),
"D": (3,7),
"E": (4,4),
"F": (4,6),
"G": (5,5),
"H": (6,4),
"I": (6,6),
"J": (7,3),
"K": (7,5),
"L": (7,7),
"M": (9,5)
}
# 辺長データを追加
for (v,w) in G.edges():
G.edges[(v, w)]["weight"] = np.sqrt((pos[v][0]-pos[w][0])**2+(pos[v][1]-pos[w][1])**2)
## グラフの離心数を計算
dict(nx.eccentricity(G, weight = "weight"))
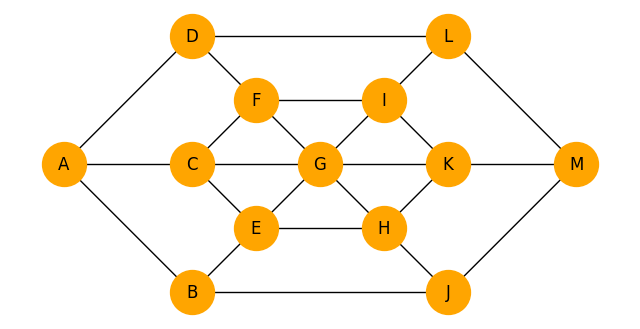
これだけ見てもあまりよく分からないと思うので、1つ1つ何を表しているのかを説明したいと思います。なおこのコードで離心数を計算したグラフは前回の記事の説明で使った以下のグラフです。(グラフの作り方を変えれば違う結果が得られます。)
コードの説明をする
事前準備
## 事前準備
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
まず最初に事前準備としていくつか便利な奴をインポートします。今回はmatplotlibとnetworkxとnumpyをインポートしました。
matplotlibはpythonでグラフを描画するときに使える便利なやつです。(関数を描画する系のグラフもグラフ理論で登場するグラフも描画できます。)
networkxはpythonでグラフ理論におけるグラフを扱うときに使える便利なやつです。
numpyはpythonで数値計算をするときに使える便利なやつです。
グラフの離心数を求めるだけならmatplotlibは必要ないですが、今回はグラフの描画も解説したいのでインポートしておきます。
グラフの作成:空の無向グラフの作成
# 空の無向グラフを作成
G = nx.Graph()
networkxでグラフを作るときはまずnx.Graph()で空の無向グラフを作るところから始まります。この空グラフに頂点や辺などの情報を追加していくというイメージです。ここではGと名前を付けたので、これ以降この空グラフを指定したいときはGを使います。
グラフの作成:頂点データの追加
# 頂点データの追加
G.add_nodes_from(["A","B","C","D","E","F","G","H","I","J","K","L","M"])
Gに頂点データを追加するには.add_nodes_from()でできます。()の中には頂点のリストを入れます。今回は頂点Aから頂点Mまでを追加します。
グラフ理論では頂点のことをよくnodeと言います。
グラフの作成:辺データの追加
# 辺データの追加
G.add_edges_from([("A","D"),("D","L"),("L","M"),("M","J"),("J","B"),("B","A"),
("C","F"),("F","I"),("I","K"),("K","H"),("H","E"),("E","C"),
("A","C"),("D","F"),("L","I"),("M","K"),("J","H"),("B","E"),
("C","G"),("F","G"),("I","G"),("K","G"),("H","G"),("E","G"),])
Gに辺データを追加するには.add_edges_from()でできます。()の中には辺のリストを入れます。例えば(“A”, “D”)は辺(A,D)を表しています。
グラフ理論では辺のことをよくedgeと言います。
グラフの作成:頂点の座標を設定
# 頂点の座標を設定する
pos = {
"A": (1,5),
"B": (3,3),
"C": (3,5),
"D": (3,7),
"E": (4,4),
"F": (4,6),
"G": (5,5),
"H": (6,4),
"I": (6,6),
"J": (7,3),
"K": (7,5),
"L": (7,7),
"M": (9,5)
}
各頂点に対して座標を設定しています。例えば頂点Aの座標は(1,5)で頂点Bの座標は(3,3)です。これらの座標データは次に説明する「辺長データの追加」のときに使います。
上のように座標を設定すると、頂点の位置関係は以下のようになります。
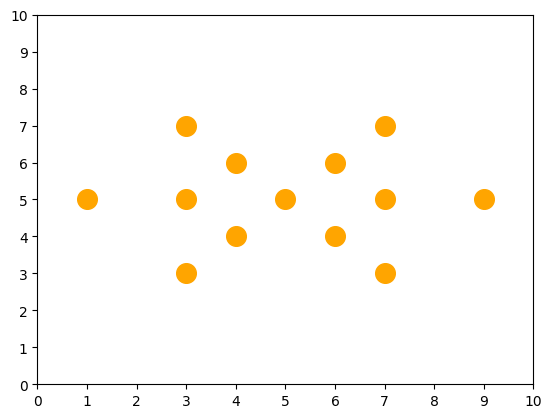
グラフの作成:辺長データの追加
# 辺長データを追加
for (v,w) in G.edges():
G.edges[(v, w)]["weight"] = np.sqrt((pos[v][0]-pos[w][0])**2+(pos[v][1]-pos[w][1])**2)
先ほど追加した全ての辺に対して辺長データを追加しています。辺の長さはユークリッド距離で定義しています。
ユークリッド距離:
2点\(a = (x_1,y_1),b = (x_2,y_2)\)の間のユークリッド距離は
\(d(a,b) = \sqrt{(x_1 – x_2)^2 + (y_1 – y_2)^2}\)
で定義される。
グラフGの辺(v,w)の長さのデータはG.edges[(v,w)][“weight”]に追加しています。今回は全ての辺に対して辺長データを追加したいのでfor文でG.edges()中の全ての辺を取り出しています。
元々Gにはweightという属性はなく、このコードで初めてweightという属性が定義されています。例えば属性の名前をlengthにしたいときはG.edges[(v,w)][“length”]でできます。
ルートの計算をするためにnumpyの.sqrt()を使っています。この()の中に計算式を入れれば\(\sqrt{\text{計算式}}\)を求めることができます。()の中に入れる計算式には1個前に設定した頂点の座標を使っています。
先ほど各頂点の座標集合にposという名前を付けました。頂点vのx座標はpos[v][0]で取り出すことができ、頂点vのy座標はpos[v][1]で取り出すことができます。頂点wについても同じようにx、y座標を取り出すことができます。
あとはユークリッド距離の定義どおりに計算式をpythonのコードに直すと上記のようになります。この時点でグラフの作成が完了しました。
グラフの離心数を求める
## グラフの離心数を計算
dict(nx.eccentricity(G, weight = "weight"))
グラフの離心数はnx.eccentricity()で求められます。()の中には離心数を求めたいグラフと辺長をどうするかの設定をしています。dict()を付けることで計算結果を辞書として返しています。(ぶっちゃけ各頂点の離心数を見るだけだったらあってもなくても変わらないです。)
例えば頂点Aの離心数は8で頂点Bの離心数は6.8284…です。これらを見ることで、例えばグラフの半径は4でグラフの直径は8でグラフの中心が頂点Gであることが分かりますね。
※グラフを描画する
本題とは外れてしまいますが、グラフを描画する方法についても解説します。結論以下のプログラムを実行することでグラフを描画することができます。
# 描画時のアスペクト比を固定して、横長のグラフが表示されるように調整
fig, ax = plt.subplots(figsize=(8, 8))
nx.draw(G, pos=pos, with_labels=True, node_size=1000, node_color="orange")
ax.set_aspect("equal") # アスペクト比を固定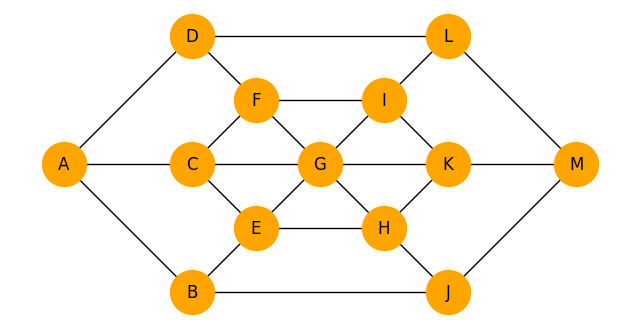
fig, axの所でグラフの大きさを設定しています。networkxのグラフを描画するときはnx.draw()を使います。()の中は順番に「描画したいグラフ」「頂点の座標」「頂点のラベル」「頂点の大きさ」「頂点の色」を設定しています。
おわりに
いかがでしたか。
今回の記事ではpythonで離心数を求める方法について解説していきました。
今後もこのような離散数学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。