This post was originally written in Japanese and translated into English. Therefore, the English may be strange in some places.
Hi! Everyone! I’m Shun! In this post, I will explain Assingment Problem.
Assignment problem is a term that appears in combinatorial optimization and can be applied in many areas in the real world.
For example, when assigning 10 employees to 10 different jobs, it is important to consider how to assign them efficiently. It is often the case that employee 1 is good at job 4, while employee 3 is not good at job 2.
Such a problem is called an assignment problem. In this post, I would like to explain how to formulate the assignment problem as an integer programming problem.
So let’s do it!
I usually write posts on statistics.
Please read my other posts! (Sorry about the Japanese version only.)
A brief introduction to this blog can be found here.
If you are interested, please take a look.
In this blog, an active science university student studying mathematical optimization will discuss various topics related to it!
I hope to share with you what I felt and what I found interesting in my study of mathematical optimization.
What is mathematical optimization anyway? According to Wikipedia,
Mathematical optimization (alternatively spelled optimisation) or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
Think with concrete examples
4 employees and 4 jobs
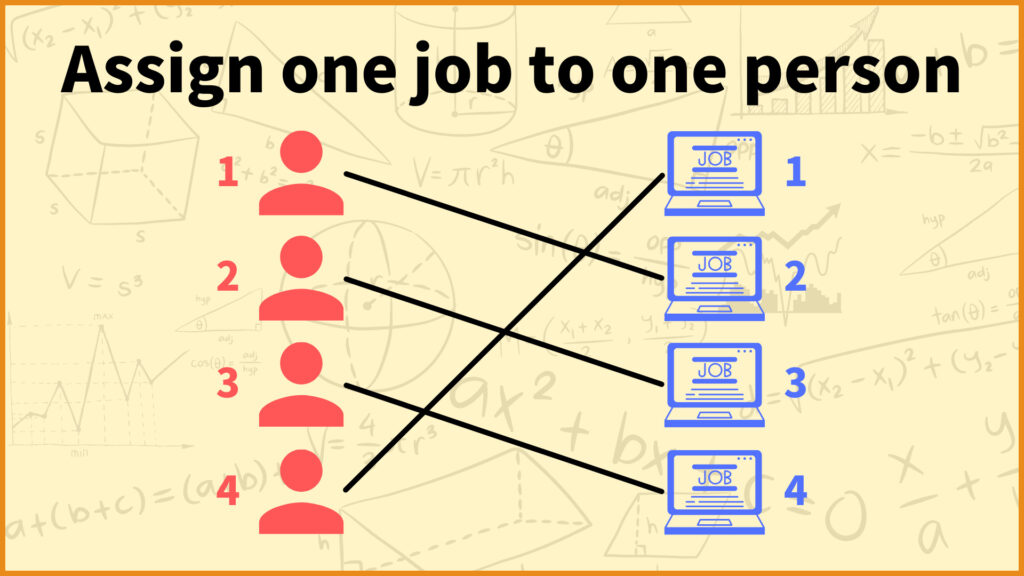
As a concrete example of an allocation problem, consider the problem of assigning jobs to employees. Consider that you are now the president of a company and you want to assign four employees to four different jobs.
At this time, each employee is always assigned exactly one job, and different employees cannot be assigned a same job.
In the example in the figure above, employee 1 is assigned job 2, employee 2 is assigned job 3, employee 3 is assigned job 4, and employee 4 is assigned job 1. However, it is not that any assignment is acceptable as long as the above conditions are met.
People have jobs they want to do and jobs they don’t want to do.

Each employee has preferences about which jobs he or she wants to do and which jobs he or she does not want to do. In order for the company to work efficiently, it is better to have each employee do the work he or she likes to do as much as possible.
Therefore, we use numbers indicating how much employees don’t want to do the job.
This time, the smaller the number, the more the employee wants to do the job, and the larger the number, the less you want to do the job.
(From now on, this number will be referred to as “a number about unwillingness.”)
In the figure above, Employee 1’s numbers are 3 for Job 1, 8 for Job 2, 1 for Job 3, and 2 for Job 4. Therefore, we can see that Employee 1 does not want to do Job 2 at all.
Conversely, we can see that employee 1 should be assigned job 3 as much as possible.
It may not be possible to meet everyone’s needs.
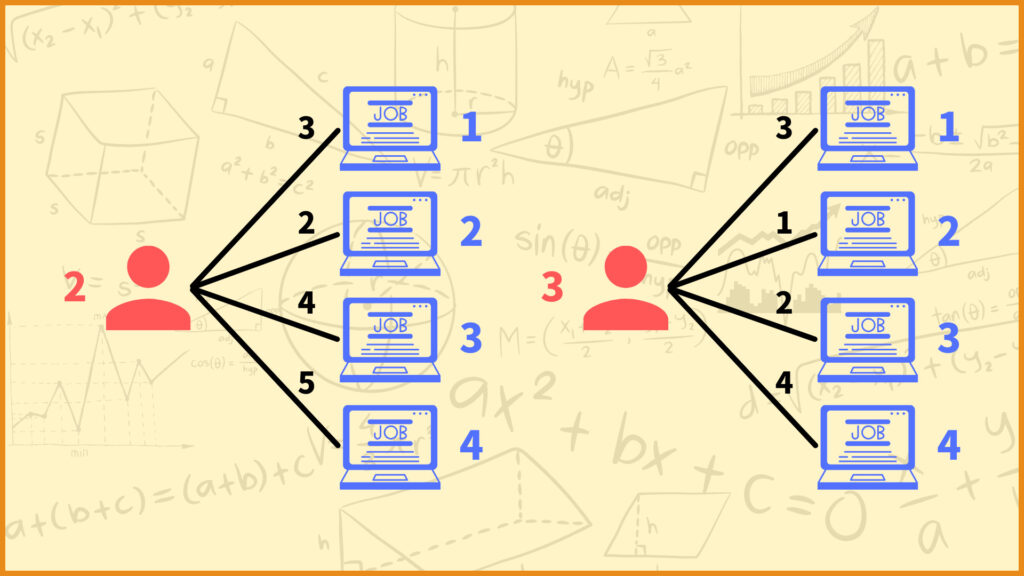
Thus, let’s consider employees 2 and 3 in the same way. we find that both employee 2 and employee 3 want to do job 2 the most. However, there is one problem here. That is
A Job can only be assigned to one person.
In other words, if you assign job 2 to employee 2, you cannot assign job 2 to employee 3. You cannot assign the first choice of job to all employees if the jobs they most want to do are same.
This is often the case in the real world.
How can we meet everyone’s needs as much as possible?
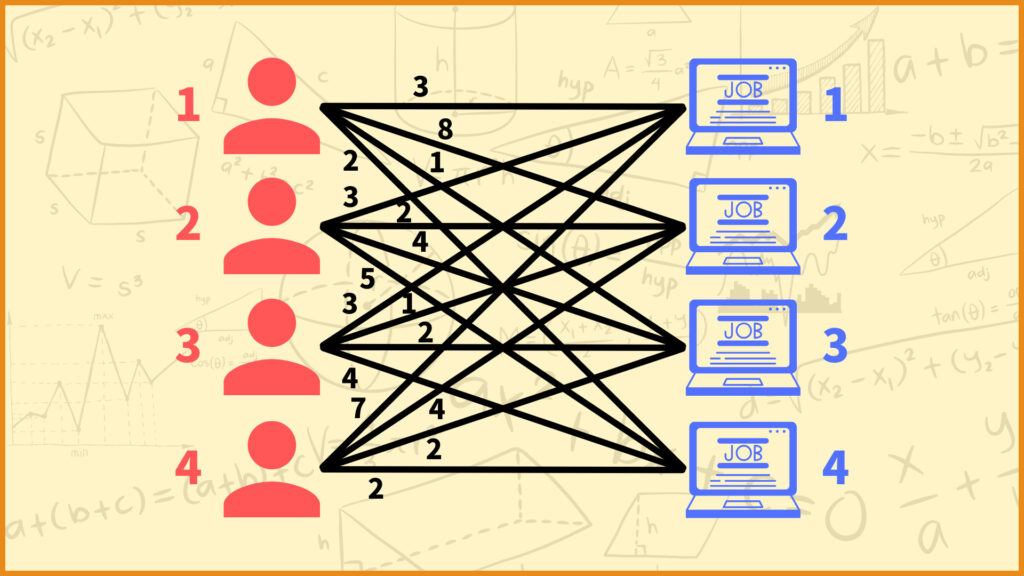
I wrote down all numbers about unwillingness of all employees. As you can see from what we have discussed so far, it is not possible to assign everyone their first choice of job. Thus, this time, we think about
「Minimizing the sum of all employees’ numbers about unwillingness」
In this way, we can realize as much as possible of the employee’s requests, while at the same time, we can achieve assignment in which one employee is in charge of one job.
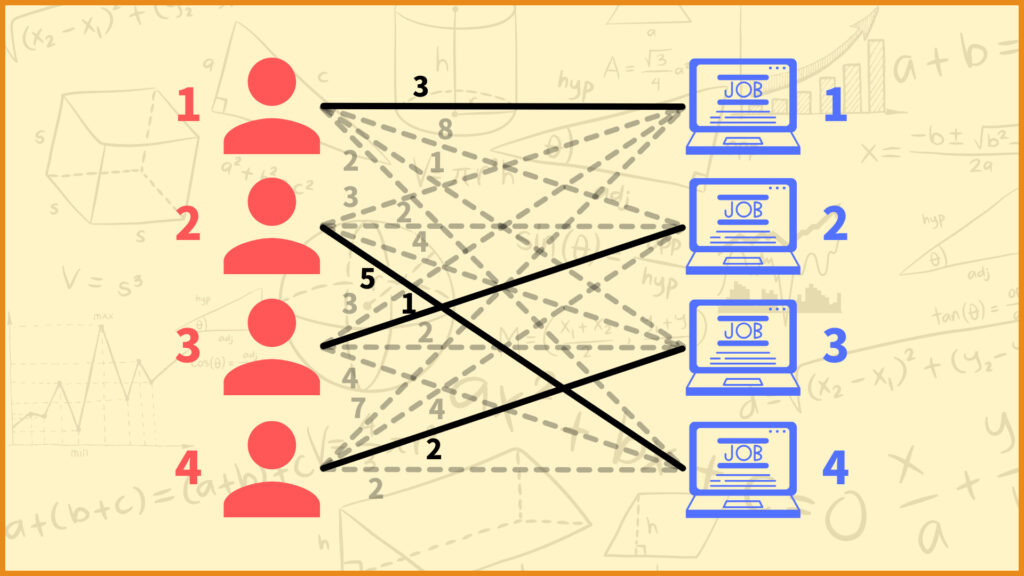
For example, as shown in the figure above, consider a case where assigning job 1 to employee 1, job 4 to employee 2, job 2 to employee 3, and job 3 to employee 4. In this case, the total numbers of unwillingness is 3+5+1+2=11.
Considered as minimum weight perfect matching
I have explained the assignment problem so far, but if you look closely, this is the same as the minimum weight perfect matching problem for complete bipartite graphs.
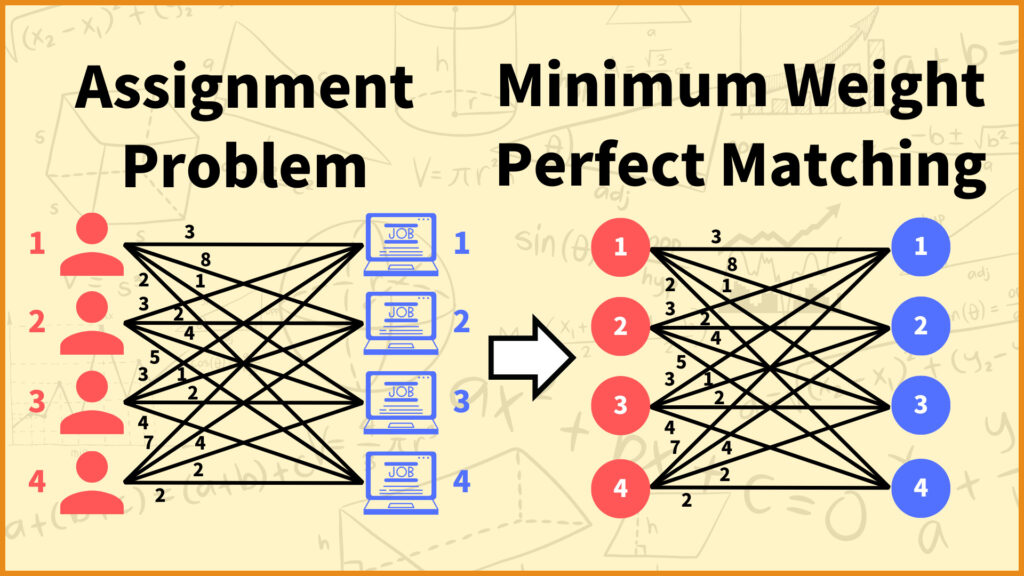
Considering the employee as the left vertex, the job as the right vertex, and the number about unwillingness of employee \(i\) for job \(j\) as the weight \(w_{ij}\) of the edge \((i,j)\), this assignment problem can be considered a minimum weight perfect matching problem in a two-part graph.
I have explained in detail how to formulate the minimum weight perfect matching problem as an integer programming problem in previous posts, so I would like to briefly explain it here.
The minimum weight perfect matching problem for complete bipartite graphs is explained in this post!
(So sorry about the Japanese version only. I plan to post an English version in the future!)
Formulate the assignment problem as an integer programming problem
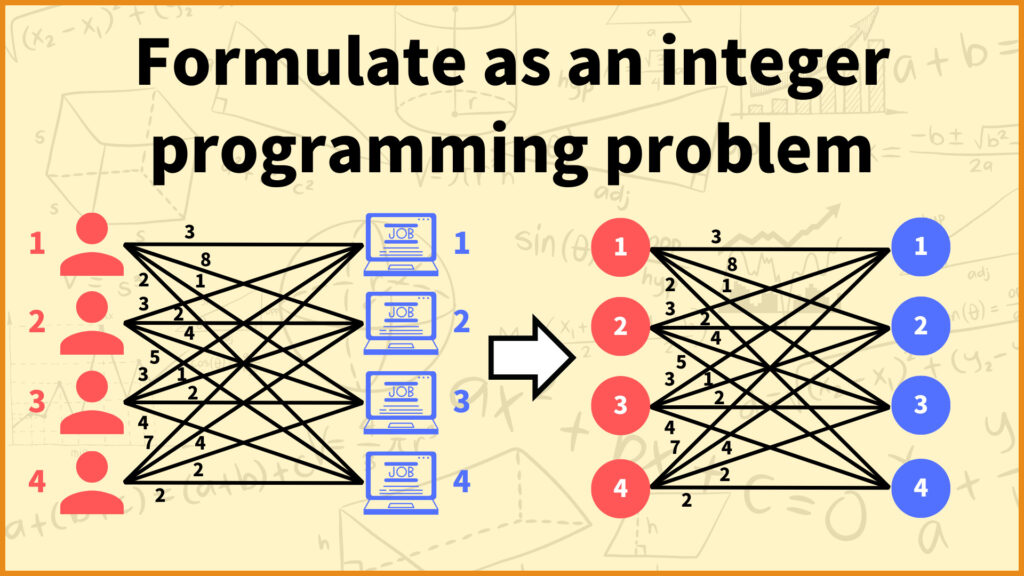
Finally, let us formulate the above assignment problem as an integer programming problem. Having said that, it can be formulated in the same way as the minimum weight perfect matching problem is formulated as an integer programming problem.
Let’s consider
“parameters/variables,”
“objective function,”
and “constraints.”
Setting parameters/variables
\(w_{ij}\) : Weight of edge \((i,j)\)
\(x_{ij}\in\{0,1\}\) : 1 if edge \((i,j)\) is chosen, 0 otherwise
We use \(w_{ij}\) as parameters and \(x_{ij}\) as variables.
\(w_{ij}\) represents the weight of the edge \((i,j)\). (Think of it as the number of unwillingness of employee \(i\) to do the job \(j\).) For example, the weight of the edge \((1,2)\) is 8, so \(w_{12} = 8\).
The variable \(x_{ij}\) is 1 if the edge \((i,j)\) is chosen, 0 otherwise. (Consider 1 if job \(j\) is assigned to employee \(i\), 0 otherwise.)
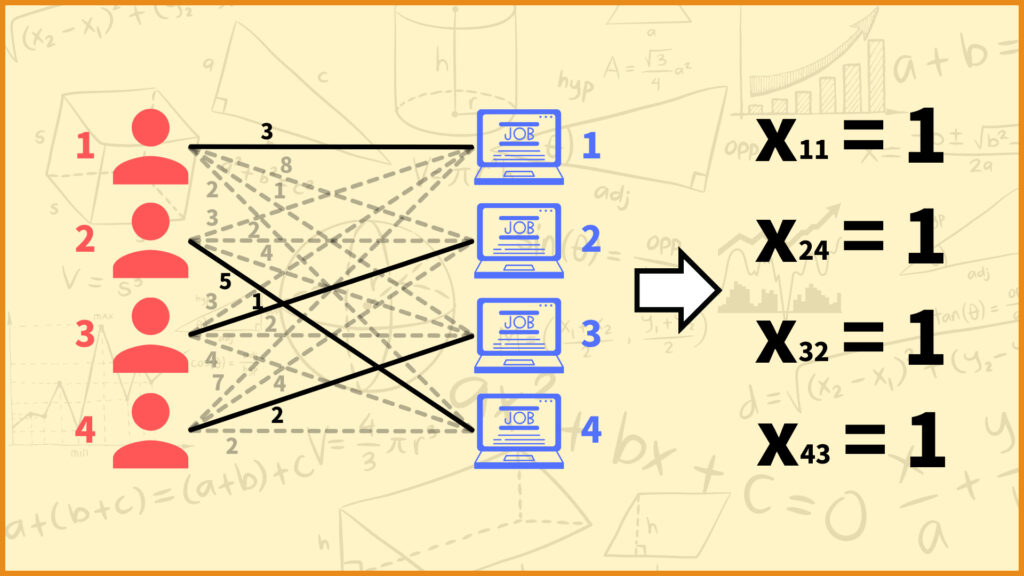
For example, in the example above, employee 1 is assigned job 1, employee 2 is assigned job 4, employee 3 is assigned job 2, and employee 4 is assigned job 3, so \(x_{11},x_{24},x_{32},x_{43}\) is \(1\).
Setting an objectve function
Next, let’s consider an objective function.
\( \sum\limits_{i=1}^4\sum\limits_{j=1}^4 w_{ij}x_{ij}\)
The objective function we consider represents
「Minimizing the sum of all employees’ numbers about unwillingness.」
Therefore, the number of unwillingness of employee \(w_{ij}\) multiplied by the variable \(x_{ij}\) and added all together is the objective function.
For instance, in the previous example, \(x_{11},x_{24},x_{32},x_{43}\) is \(1\) and the other variables are \(0\), so the objective function’s value is equal to \(w_{11}+w_{24}+w_{32}+w_{43}\).
Setting constraints
the employee-side constraints:
\(\sum\limits_{j=1}^4 x_{ij}=1 \;\;\;\; (i = 1,2,3,4)\)
the job-side constraints:
\(\sum\limits_{i=1}^4 x_{ij}=1 \;\;\;\; (j = 1,2,3,4)\)
For the employee-side constraints, this means that each employee is always assigned one job. For example, if we look at the constraints on employee 1 (\(i=1\))
\(\sum\limits_{j=1}^4 x_{1j}=x_{11}+x_{12}+x_{13}+x_{14} = 1\).
For example, if \(x_{12} = 1\) (employee 1 is assigned job 2), then automatically \(x_{11}=x_{13}=x_{14}=0\), which means that employee 1 is not assigned jobs 1, 3 and 4.
This constraint means if any one of the variables is 1, all others are 0. We want to impose this constraint on \(i=2,3,4\) as well, so \((i=1,2,3,4)\).
As for the job-side constraints, they are the same as the employee-side constraints: each job is always assigned to one employee.
Summarize as an integer programming problem
Finally, let us put these together and formulate them as an integer programming problem.
Formularization:
\(\min \;\;\; \sum\limits_{i=1}^4 \sum\limits_{j=1}^4 w_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j=1}^4 x_{ij}=1 \;\;\;\; (i = 1,2,3,4)\)
\(\;\;\;\;\;\;\;\;\;\sum\limits_{i=1}^4 x_{ij}=1 \;\;\;\; (j = 1,2,3,4)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;(i=1,2,3,4 \; j=1,2,3,4)\)
In the next posts, I would like to express the integer programming problem formulated in this post in python and actually solve the problem!
Click here to read the next posts!
Currently in production
Conclusion
How was it?
In this posts, we explained the allocation problem.
I will continue to write posts like this one on combinatorial optimization!
Thank you for reading this until the end.